Ikosidodekaeder

Polyeder Ikosidodekaeder
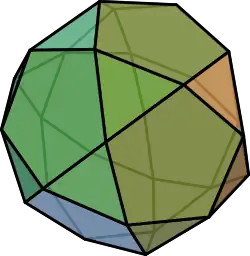
3D-Ansicht eines Ikosidodekaeders (Animation)
Anzahl der Seitenflächen	32
Art der Seitenflächen	20 Dreiecke, 12 Fünfecke
Anzahl Ecken	30
Art der Ecken	30 × {3.5.3.5}
Anzahl Kanten	60
Symmetriegruppe	Ikosaedergruppe ${\displaystyle I_{h}}$
Schläfli-Symbol	r{3,5} oder r{5,3}
dual zu	Rhombentriakontaeder
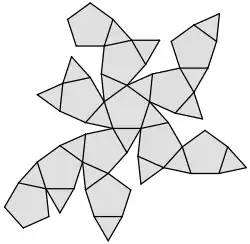Körpernetz eines Ikosidodekaeders

Das Ikosidodekaeder ist ein Polyeder (Vielflächner) mit 32 Flächen (12 Fünfecke und 20 gleichseitige Dreiecke), 30 Ecken und 60 Kanten gleicher Länge.

Es wird durch die Schnittmenge der Durchdringung eines Dodekaeders und Ikosaeders beschrieben, welche auch in seinem Namen auftauchen.

Es ist ein archimedischer Körper und der duale Körper zum Rhombentriakontaeder.

Jeweils zehn Kanten des Ikosidodekaeders bilden die Kanten eines regelmäßigen Zehnecks. Insgesamt gibt es sechs solcher unabhängiger, gleichseitiger Zehnecke in einem Ikosidodekaeder.

Ein Ikosidodekaeder lässt sich aus einem Dodekaeder oder Ikosaeder durch Rektifikation (Abstumpfen bis zu den Kantenmittelpunkten) erzeugen.

Durch die geraden Permutationen von

$${\displaystyle (\pm 1,0,0),\qquad {\tfrac {1}{2}}\left(\pm \Phi ,\pm {\tfrac {1}{\Phi }},\pm 1\right)}$$

erhält man kartesische Koordinaten der Ecken eines Ikosidodekaeders. Dabei ist ${\displaystyle \Phi ={\tfrac {1}{2}}(1+{\sqrt {5}})}$ das Verhältnis des Goldenen Schnitts.^[1]

Größen eines Ikosidodekaeders mit Kantenlänge a
Volumen	${\displaystyle V={\frac {a^{3}}{6}}\left(45+17{\sqrt {5}}\right)}$
Oberflächeninhalt	${\displaystyle A_{O}=a^{2}\left(5{\sqrt {3}}+3{\sqrt {25+10{\sqrt {5}}}}\right)}$
Umkugelradius	${\displaystyle R={\frac {a}{2}}\left(1+{\sqrt {5}}\right)}$
Kantenkugelradius	${\displaystyle r={\frac {a}{2}}{\sqrt {5+2{\sqrt {5}}}}}$
Flächenwinkel  ≈ 142° 37′ 21″	${\displaystyle \cos \,\alpha =-{\sqrt {\frac {5+2{\sqrt {5}}}{15}}}}$
Eckenraumwinkel  ≈ 1,1694 π	${\displaystyle \Omega =2\pi -\arccos \left({\frac {3+16{\sqrt {5}}}{-45}}\right)}$
Sphärizität  ≈ 0,95102	${\displaystyle \Psi ={\frac {\sqrt[{3}]{10\,\pi \left(347+153{\sqrt {5}}\right)}}{5{\sqrt {3}}+3{\sqrt {25+10{\sqrt {5}}}}}}}$

Commons: Ikosidodekaeder – Sammlung von Bildern, Videos und Audiodateien

• Eric W. Weisstein: Ikosidodekaeder. In: MathWorld (englisch).

1. ↑ Marc de Graef, Michael McHenry: Structure of Materials: An Introduction to Crystallography, Diffraction and Symmetry. 2. Auflage. Cambridge University Press, 2012, ISBN 978-1-139-56047-4, S. 500 (englisch).