Umkugel

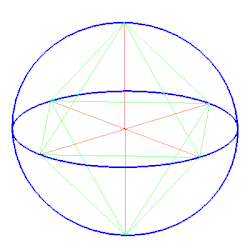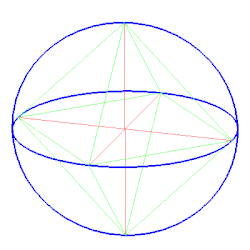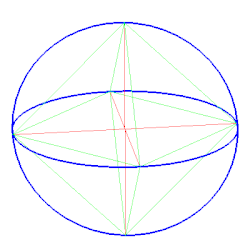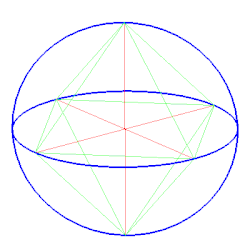
Bei der Umkugel eines Polyeders handelt es sich um eine Kugel, auf der alle Ecken des gegebenen Polyeders liegen. Die Umkugel in der Raumgeometrie ist die Entsprechung zum Umkreis eines Polygons in der ebenen Geometrie. Nicht alle Polyeder besitzen eine Umkugel.

Der Mittelpunkt einer Umkugel muss von allen Ecken gleich weit entfernt sein. Er muss sich daher auf allen Symmetrieebenen von je zwei Ecken befinden. Da die Schnittmenge dieser Ebenen im Allgemeinen leer ist, besitzen nur spezielle Polyeder eine Umkugel, insbesondere alle Tetraeder^[1], die fünf Platonischen Körper, sämtliche Archimedische Körper, sowie alle geraden Dreiecksprismen.

Die kleinste Kugel, welche ein Objekt umschließt (aber nicht zwingend alle Eckpunkte berührt), ist der kugelförmige Hüllkörper des Objekts.

• Inkugel
• Kantenkugel
• Umkreis

Wiktionary: Umkugel – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

• Eric W. Weisstein: Circumsphere. In: MathWorld (englisch).
• Venndigramm zur Beschreibung von Um-, In- und Kantenkugeln bei Polyedern

1. ↑ Andreas Filler: Elementare Lineare Algebra (= Mathematik Primarstufe und Sekundarstufe I + II). Spektrum Akademischer Verlag, Heidelberg 2011, ISBN 978-3-8274-2412-9, S. 67.