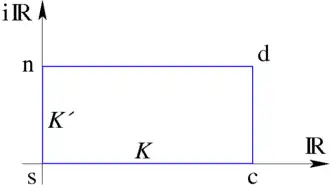
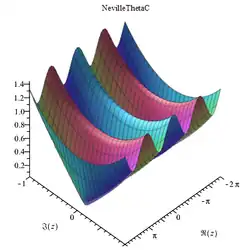
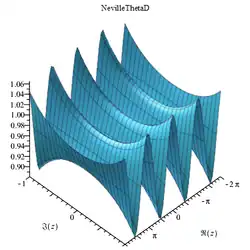
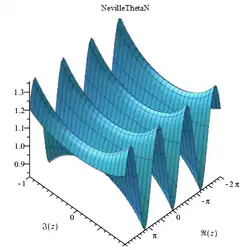
Nevillesche Thetafunktionen

Die nevilleschen Thetafunktionen bilden in der Mathematik eine Funktionengruppe, die zu den elliptischen Funktionen zählt. Sie wurden von dem englischen Mathematiker Eric Harold Neville eingeführt^[1] und haben die Bezeichnungen ${\displaystyle \theta _{s}}$, ${\displaystyle \theta _{c}}$, ${\displaystyle \theta _{d}}$ und ${\displaystyle \theta _{n}}$. Die Indizes beziehen sich auf die abgebildete Hilfskonstruktion, nämlich ein achsenparalleles Rechteck in der komplexen Zahlenebene mit den Ecken ${\displaystyle s=0}$, ${\displaystyle c=K}$, ${\displaystyle d=K+\mathrm {i} K'}$ und ${\displaystyle n=\mathrm {i} K'}$. Dabei sind ${\displaystyle K}$ und ${\displaystyle K'}$ die Seitenlängen des Rechtecks, die bestimmten elliptischen Integralen entsprechen. Der Index gibt an, in welcher Ecke die Funktion eine Nullstelle hat.^[2] Beispielsweise hat die Funktion ${\displaystyle \theta _{c}}$ bei ${\displaystyle c}$ eine Nullstelle.

Als elliptische Funktionen sind die nevilleschen Funktionen doppelt-periodisch. Die zwölf jacobischen elliptischen Funktionen lassen sich auf einheitliche Weise mithilfe der nevilleschen Thetafunktionen definieren.

Als Erstes wird das vollständige elliptische Integral erster Art in seiner Standardform definiert:

${\displaystyle K(\varepsilon )=\int _{0}^{1}{\frac {2}{\sqrt {(x^{2}+1)^{2}-4\,\varepsilon ^{2}x^{2}}}}\,\mathrm {d} x}$

${\displaystyle K'(\varepsilon )=\int _{0}^{1}{\frac {2}{\sqrt {(x^{2}-1)^{2}+4\,\varepsilon ^{2}x^{2}}}}\,\mathrm {d} x}$

Das komplementäre Integral ${\displaystyle K'}$ ist gleich dem K-Integral des pythagoräisch komplementären Moduls:

${\displaystyle K'(k)=K({\sqrt {1-k^{2}}}\,)}$

Basierend darauf wird das elliptische Nomen in seiner Standardform so definiert:

${\displaystyle q(k)=\exp \left(-\pi \,K'(k)/K(k)\right)}$

Als Nächstes wird das reduzierte vollständige elliptische Integral erster Art und das reduzierte elliptische Nomen definiert:

${\displaystyle {\bar {K}}(k)={\frac {2}{\pi }}K(k)}$

${\displaystyle {\bar {q}}(k)={\sqrt[{4}]{k^{-2}q(k)}}}$

Die nun beschriebenen jeweiligen reduzierten Formen werden mit einem Querbalken über den betroffenen Buchstaben dargestellt.

Die nevilleschen Thetafunktionen lassen sich mithilfe der jacobischen Thetafunktionen ${\displaystyle \theta _{1}}$ bis ${\displaystyle \theta _{4}}$ definieren:^[3]

${\displaystyle {\begin{aligned}\theta _{s}(z)&={\frac {2K\theta _{1}(v)}{\theta _{1}'(0)}}\\\theta _{c}(z)&={\frac {\theta _{2}(v)}{\theta _{2}(0)}}\\\theta _{d}(z)&={\frac {\theta _{3}(v)}{\theta _{3}(0)}}\\\theta _{n}(z)&={\frac {\theta _{4}(v)}{\theta _{4}(0)}}\end{aligned}}}$

Dabei ist ${\displaystyle v={\frac {\pi z}{2K}}}$. Das zweite Argument (${\displaystyle k}$ oder ${\displaystyle m=k^{2}}$) wurde weggelassen.

Nach Edmund Taylor Whittaker und George Neville Watson sind die Neville Thetafunktionen^[4][5][6] als Quotienten aus Jacobischer Thetafunktion und Theta-Nullwert definiert:

${\displaystyle \theta _{c}(z;k)=\vartheta _{10}{\bigl [}q(k){\bigr ]}^{-1}\vartheta _{10}{\bigl [}z\div {\bar {K}}(k);q(k){\bigr ]}=\cos {\bigl [}z\div {\bar {K}}(k){\bigr ]}\prod _{n=1}^{\infty }{\bigl [}1+q(k)^{2n}{\bigr ]}^{-2}{\bigl \{}1+2q(k)^{2n}\cos {\bigl [}2z\div {\bar {K}}(k){\bigr ]}+q(k)^{4n}{\bigr \}}}$

${\displaystyle \theta _{d}(z;k)=\vartheta _{00}{\bigl [}q(k){\bigr ]}^{-1}\vartheta _{00}{\bigl [}z\div {\bar {K}}(k);q(k){\bigr ]}=\prod _{n=1}^{\infty }{\bigl [}1+q(k)^{2n-1}{\bigr ]}^{-2}{\bigl \{}1+2q(k)^{2n-1}\cos {\bigl [}2z\div {\bar {K}}(k){\bigr ]}+q(k)^{4n-2}{\bigr \}}}$

${\displaystyle \theta _{n}(z;k)=\vartheta _{01}{\bigl [}q(k){\bigr ]}^{-1}\vartheta _{01}{\bigl [}z\div {\bar {K}}(k);q(k){\bigr ]}=\prod _{n=1}^{\infty }{\bigl [}1-q(k)^{2n-1}{\bigr ]}^{-2}{\bigl \{}1-2q(k)^{2n-1}\cos {\bigl [}2z\div {\bar {K}}(k){\bigr ]}+q(k)^{4n-2}{\bigr \}}}$

${\displaystyle \theta _{s}(z;k)={\bar {K}}(k)\sin {\bigl [}z\div {\bar {K}}(k){\bigr ]}\prod _{n=1}^{\infty }{\bigl [}1-q(k)^{2n}{\bigr ]}^{-2}{\bigl \{}1-2q(k)^{2n}\cos {\bigl [}2z\div {\bar {K}}(k){\bigr ]}+q(k)^{4n}{\bigr \}}}$

So sind die Nevilleschen Thetafunktionen über die Lambertschen Reihen^[7][8][9] definiert:

${\displaystyle \theta _{c}(z;k)=2\,{\bar {q}}(k)\,{\bar {K}}(k)^{-1/2}\,\sum _{n=1}^{\infty }q(k)^{n(n-1)}\cos {\bigl [}(2n-1){\bar {K}}(k)^{-1}z{\bigr ]}}$

${\displaystyle \theta _{d}(z;k)={\bar {K}}(k)^{-1/2}\,{\biggl \{}1+2\,\sum _{n=1}^{\infty }q(k)^{n^{2}}\cos {\bigl [}2\,n\,{\bar {K}}(k)^{-1}z{\bigr ]}{\biggr \}}}$

${\displaystyle \theta _{n}(z;k)=(1-k^{2})^{-1/4}{\bar {K}}(k)^{-1/2}\,{\biggl \{}1+2\,\sum _{n=1}^{\infty }(-1)^{n}q(k)^{n^{2}}\cos {\bigl [}2\,n\,{\bar {K}}(k)^{-1}z{\bigr ]}{\biggr \}}}$

${\displaystyle \theta _{s}(z;k)=2\,(1-k^{2})^{-1/4}{\bar {q}}(k)\,{\bar {K}}(k)^{-1/2}\,\sum _{n=1}^{\infty }(-1)^{n-1}q(k)^{n(n-1)}\sin {\bigl [}(2n-1){\bar {K}}(k)^{-1}z{\bigr ]}}$

Sehr schnell konvergent sind folgende Summenreihen für die Nevilleschen Thetafunktionen:

${\displaystyle \theta _{c}(z;k)=|k|^{-1/2}{\bigl (}{\frac {\pi }{2}}{\bigr )}^{1/2}K'(k)^{-1/2}\sum _{n=-\infty }^{\infty }(-1)^{n}\exp {\biggl \{}-\pi \,{\frac {K(k)}{K'(k)}}{\biggl [}n+{\frac {z}{2\,K(k)}}{\biggr ]}^{2}{\biggr \}}}$

${\displaystyle \theta _{d}(z;k)={\bigl (}{\frac {\pi }{2}}{\bigr )}^{1/2}K'(k)^{-1/2}\sum _{n=-\infty }^{\infty }\exp {\biggl \{}-\pi \,{\frac {K(k)}{K'(k)}}{\biggl [}n+{\frac {z}{2\,K(k)}}{\biggr ]}^{2}{\biggr \}}}$

${\displaystyle \theta _{n}(z;k)=(1-k^{2})^{-1/4}{\bigl (}{\frac {\pi }{2}}{\bigr )}^{1/2}K'(k)^{-1/2}\sum _{n=-\infty }^{\infty }\exp {\biggl \{}-\pi \,{\frac {K(k)}{K'(k)}}{\biggl [}n+{\frac {1}{2}}+{\frac {z}{2\,K(k)}}{\biggr ]}^{2}{\biggr \}}}$

${\displaystyle \theta _{s}(z;k)=|k|^{-1/2}(1-k^{2})^{-1/4}{\bigl (}{\frac {\pi }{2}}{\bigr )}^{1/2}K'(k)^{-1/2}\sum _{n=-\infty }^{\infty }(-1)^{n}\exp {\biggl \{}-\pi \,{\frac {K(k)}{K'(k)}}{\biggl [}n+{\frac {1}{2}}-{\frac {z}{2\,K(k)}}{\biggr ]}^{2}{\biggr \}}}$

So wird die Ramanujansche Thetafunktion definiert:

${\displaystyle \vartheta _{R}(v;w)=\sum _{n=-\infty }^{\infty }v^{n(n+1)/2}\,w^{n(n-1)/2}=\sum _{n=-\infty }^{\infty }v^{\bigtriangleup (n)}\,w^{\bigtriangleup (n-1)}}$

${\displaystyle \vartheta _{R}(v;w)=1+v+w+\sum _{n=1}^{\infty }(vw)^{\bigtriangleup (n)}(v^{n+1}+w^{n+1})}$

${\displaystyle \vartheta _{R}(v;w)=(-v;vw)_{\infty }(-w;vw)_{\infty }(vw;vw)_{\infty }}$

${\displaystyle \vartheta _{R}(v;w)=1+{\frac {2v}{\sqrt {\pi }}}\int _{0}^{\infty }\exp(-x^{2}){\biggl \{}{\frac {1-v{\sqrt {vw}}\cos {\bigl [}{\sqrt {-2\ln(vw)}}\,x{\bigr ]}}{1-2v{\sqrt {vw}}\cos {\bigl [}{\sqrt {-2\ln(vw)}}\,x{\bigr ]}+v^{3}w}}{\biggr \}}\,\mathrm {d} x\,+}$

${\displaystyle +\,{\frac {2w}{\sqrt {\pi }}}\int _{0}^{\infty }\exp(-x^{2}){\biggl \{}{\frac {1-w{\sqrt {vw}}\cos {\bigl [}{\sqrt {-2\ln(vw)}}\,x{\bigr ]}}{1-2w{\sqrt {vw}}\cos {\bigl [}{\sqrt {-2\ln(vw)}}\,x{\bigr ]}+vw^{3}}}{\biggr \}}\,\mathrm {d} x}$

Die Dreieckssymbole in den Exponenten der beiden obersten Formeln dieser Liste stellen die Funktion von der Folge der Dreieckszahlen dar. Durch die Tatsache, dass sich die Exponenten in den genannten Summenreihen bezüglich des Index in der Funktion der Dreieckszahlen verhalten, konvergieren die gezeigten Summenreihen sehr schnell mit einem quadratischen Wachstum der richtigen Nachkommastellen. Mit dem Unendlichkeitssymbol in Basislage wird das Nomen-Pochhammer-Produkt dargestellt, welches die unendliche Variante des verallgemeinerten Pochhammer-Produktes ist. Die am Ende dieser Liste dargestellten Integrale von Produkten aus Gaussscher Glockenkurvenfunktion und trigonometrischem Funktionenbruch wurden in der Universität Georgia durch die kanadische Mathematikerin Maxie Schmidt und ihre Arbeitsgruppe erforscht und beschreiben sogenannte uneigentliche Integrale. Die Nevillesche Thetafunktion ${\displaystyle \theta _{d}}$ kann mit Hilfe der Ramanujanschen Thetafunktion auf diese Weise dargestellt werden:

${\displaystyle \theta _{d}(z;k)={\bigl (}{\frac {\pi }{2}}{\bigr )}^{1/2}K'(k)^{-1/2}\exp {\biggl [}-{\frac {\pi \,z^{2}}{4\,K(k)\,K'(k)}}{\biggr ]}\vartheta _{R}{\biggl \{}\exp {\biggl [}\pi \,{\frac {z-K(k)}{K'(k)}}{\biggr ]};\exp {\biggl [}\pi \,{\frac {-z-K(k)}{K'(k)}}{\biggr ]}{\biggr \}}}$

Umgekehrt gilt dementsprechend:

${\displaystyle \vartheta _{R}(v;w)=\exp {\biggl [}-{\frac {\ln(v\div w)^{2}}{8\ln(vw)}}{\biggr ]}\vartheta _{00}({\sqrt {vw}}\,)\,\theta _{d}{\bigl [}{\frac {1}{4}}\ln(v\div w)\vartheta _{00}({\sqrt {vw}}\,)^{2};\psi _{H}({\sqrt {vw}}\,)^{4}{\bigr ]}}$

Sukzessiv kann darauf zu dieser Nevilleschen Thetafunktion geführt werden:

${\displaystyle \theta _{n}(z;k)=(1-k^{2})^{-1/4}\theta _{d}{\bigl [}K(k)-z;k{\bigr ]}}$

Hinweis: Das Symbol ${\displaystyle \lambda ^{\ast }}$ bezeichnet die Lambda-Stern-Funktion.

Im Folgenden werden die zugehörigen Werte in Kombination mit dem lemniskatisch elliptischen Modul ${\displaystyle k=\lambda ^{*}(1)={\tfrac {1}{2}}{\sqrt {2}}}$ niedergeschrieben:

Werte für ${\displaystyle \theta _{c}}$:

${\displaystyle \theta _{c}{\bigl [}{\tfrac {1}{2}}K({\tfrac {1}{2}}{\sqrt {2}});{\tfrac {1}{2}}{\sqrt {2}}{\bigr ]}=2^{-3/16}{\sqrt[{4}]{{\sqrt {2}}-1}}}$

${\displaystyle \theta _{c}{\bigl [}{\tfrac {1}{3}}K({\tfrac {1}{2}}{\sqrt {2}});{\tfrac {1}{2}}{\sqrt {2}}{\bigr ]}=2^{-1/4}3^{1/8}(2+{\sqrt {3}}\,)^{-1/12}}$

Werte für ${\displaystyle \theta _{d}}$:

${\displaystyle \theta _{d}{\bigl [}K({\tfrac {1}{2}}{\sqrt {2}});{\tfrac {1}{2}}{\sqrt {2}}{\bigr ]}=2^{-1/4}}$

${\displaystyle \theta _{d}{\bigl [}{\tfrac {1}{2}}K({\tfrac {1}{2}}{\sqrt {2}});{\tfrac {1}{2}}{\sqrt {2}}{\bigr ]}=2^{-7/16}{\sqrt[{4}]{{\sqrt {2}}+1}}}$

${\displaystyle \theta _{d}{\bigl [}{\tfrac {2}{3}}K({\tfrac {1}{2}}{\sqrt {2}});{\tfrac {1}{2}}{\sqrt {2}}{\bigr ]}=2^{-1/2}{\sqrt[{6}]{2+{\sqrt {3}}}}}$

${\displaystyle \theta _{d}{\bigl [}{\tfrac {2}{5}}K({\tfrac {1}{2}}{\sqrt {2}});{\tfrac {1}{2}}{\sqrt {2}}{\bigr ]}=2^{-1/2}{\sqrt[{5}]{2({\sqrt {5}}+2)\cos({\tfrac {1}{20}}\pi )\tan({\tfrac {3}{20}}\pi )}}}$

${\displaystyle \theta _{d}{\bigl [}{\tfrac {4}{5}}K({\tfrac {1}{2}}{\sqrt {2}});{\tfrac {1}{2}}{\sqrt {2}}{\bigr ]}=2^{-1/2}{\sqrt[{5}]{2({\sqrt {5}}+2)\sin({\tfrac {1}{20}}\pi )\cot({\tfrac {3}{20}}\pi )}}}$

Diese Werte kommen durch Einsatz vom Modul ${\displaystyle \lambda ^{*}(2)={\sqrt {2}}-1}$ hervor:

${\displaystyle \theta _{d}{\bigl [}K({\sqrt {2}}-1);{\sqrt {2}}-1{\bigr ]}=2^{1/4}({\sqrt {2}}+1)^{-1/4}}$

${\displaystyle \theta _{d}{\bigl [}{\tfrac {1}{3}}K({\sqrt {2}}-1);{\sqrt {2}}-1{\bigr ]}=2^{-1/4}({\sqrt {2}}+1)^{-1/4}({\sqrt {3}}+{\sqrt {2}}\,)^{1/3}}$

${\displaystyle \theta _{d}{\bigl [}{\tfrac {2}{3}}K({\sqrt {2}}-1);{\sqrt {2}}-1{\bigr ]}=\sec({\tfrac {1}{8}}\pi )\sin({\tfrac {5}{24}}\pi )({\sqrt {3}}+{\sqrt {2}}\,)^{1/3}}$

${\displaystyle \theta _{n}{\bigl [}{\tfrac {2}{5}}K({\sqrt {2}}-1);{\sqrt {2}}-1{\bigr ]}=2^{-1/2}{\text{g}}(50)^{1/2}\tan {\bigl \{}{\tfrac {1}{2}}\operatorname {arccot} {\bigl [}{\text{g}}(50){\bigr ]}{\bigr \}}^{1/10}\cot {\bigl \{}{\tfrac {1}{2}}\arctan {\bigl [}{\text{g}}(50){\bigr ]}{\bigr \}}^{3/10}}$

${\displaystyle \theta _{n}{\bigl [}{\tfrac {4}{5}}K({\sqrt {2}}-1);{\sqrt {2}}-1{\bigr ]}=2^{-1/2}{\text{g}}(50)^{1/2}\cot {\bigl \{}{\tfrac {1}{2}}\operatorname {arccot} {\bigl [}{\text{g}}(50){\bigr ]}{\bigr \}}^{1/10}\tan {\bigl \{}{\tfrac {1}{2}}\arctan {\bigl [}{\text{g}}(50){\bigr ]}{\bigr \}}^{3/10}}$

Dabei steht ${\displaystyle {\text{g}}(50)}$ für folgende Konstante:

${\displaystyle {\text{g}}(50)=w_{R5}({\sqrt {2}}-1)=2\,[\exp(-5\,{\sqrt {2}}\,\pi );\exp(-10\,{\sqrt {2}}\,\pi )]_{\infty }[\exp(-{\sqrt {2}}\,\pi );\exp(-2\,{\sqrt {2}}\,\pi )]_{\infty }^{-5}=}$

${\displaystyle ={\tfrac {1}{2}}{\bigl \{}{\tfrac {4}{3}}{\sqrt {2}}\cos({\tfrac {1}{10}}\pi )\cosh[{\tfrac {1}{3}}\operatorname {artanh} ({\tfrac {3}{8}}{\sqrt {6}})]+{\tfrac {1}{3}}\tan({\tfrac {1}{5}}\pi ){\bigr \}}^{2}-{\tfrac {1}{2}}=}$

${\displaystyle ={\bigl \langle }{\tfrac {1}{2}}-{\tfrac {1}{2}}{\bigl \{}{\tfrac {4}{3}}{\sqrt {2}}\sin({\tfrac {1}{5}}\pi )\cosh[{\tfrac {1}{3}}\operatorname {artanh} ({\tfrac {3}{8}}{\sqrt {6}})]-{\tfrac {1}{3}}\cot({\tfrac {1}{10}}\pi ){\bigr \}}^{2}{\bigr \rangle }^{-1}=}$

${\displaystyle =\Phi ^{-1}\cot {\bigl [}{\tfrac {1}{4}}\pi -\arctan {\bigl (}{\tfrac {1}{3}}{\sqrt {5}}-{\tfrac {1}{3}}{\sqrt[{3}]{6{\sqrt {30}}+4{\sqrt {5}}}}+{\tfrac {1}{3}}{\sqrt[{3}]{6{\sqrt {30}}-4{\sqrt {5}}}}{\bigr )}{\bigr ]}=}$

${\displaystyle \approx 2{,}12190403802900202926}$

Zugehörige Gleichungen:

${\displaystyle {\text{g}}(50)^{6}-2\,{\text{g}}(50)^{5}-2\,{\text{g}}(50)-1=0}$

${\displaystyle {\text{g}}(50)^{3}-{\text{g}}(50)^{2}-\Phi \,{\text{g}}(50)-\Phi =0}$

Diejenigen Werte, welche mit dem Modul ${\displaystyle \lambda ^{*}(3)=\sin({\tfrac {1}{12}}\pi )}$ in Verbindung stehen, werden Äquianharmonische Werte genannt:

${\displaystyle \theta _{c}{\bigl \{}{\tfrac {1}{3}}K{\bigl [}\sin({\tfrac {1}{12}}\pi ){\bigr ]};\sin({\tfrac {1}{12}}\pi ){\bigr \}}=2^{-1/6}3^{-7/12}(2+{\sqrt {3}})^{1/4}({\sqrt[{3}]{4}}-{\sqrt[{3}]{2}}+1)}$

${\displaystyle \theta _{c}{\bigl \{}{\tfrac {2}{3}}K{\bigl [}\sin({\tfrac {1}{12}}\pi ){\bigr ]};\sin({\tfrac {1}{12}}\pi ){\bigr \}}={\tfrac {1}{6}}{\sqrt[{3}]{18}}\,(-{\sqrt[{3}]{4}}+{\sqrt {3}}+1)}$

${\displaystyle \theta _{d}{\bigl \{}{\tfrac {1}{3}}K{\bigl [}\sin({\tfrac {1}{12}}\pi ){\bigr ]};\sin({\tfrac {1}{12}}\pi ){\bigr \}}={\tfrac {1}{6}}\,{\sqrt[{3}]{9}}\,(2+{\sqrt {3}})^{-1/4}({\sqrt[{3}]{2}}+{\sqrt {3}}+1)}$

${\displaystyle \theta _{d}{\bigl \{}{\tfrac {2}{3}}K{\bigl [}\sin({\tfrac {1}{12}}\pi ){\bigr ]};\sin({\tfrac {1}{12}}\pi ){\bigr \}}={\tfrac {1}{6}}{\sqrt[{3}]{18}}\,({\sqrt[{3}]{2}}+1)}$

${\displaystyle \theta _{n}{\bigl \{}{\tfrac {1}{3}}K{\bigl [}\sin({\tfrac {1}{12}}\pi ){\bigr ]};\sin({\tfrac {1}{12}}\pi ){\bigr \}}=2^{-1/6}3^{-1/3}(2+{\sqrt {3}})^{-1/4}({\sqrt[{3}]{2}}+1)}$

${\displaystyle \theta _{n}{\bigl \{}{\tfrac {2}{3}}K{\bigl [}\sin({\tfrac {1}{12}}\pi ){\bigr ]};\sin({\tfrac {1}{12}}\pi ){\bigr \}}={\tfrac {1}{6}}{\sqrt[{3}]{9}}\,({\sqrt {3}}-1)\,({\sqrt[{3}]{2}}+{\sqrt {3}}+1)}$

Eingesetzt wird nun der Modulwert ${\displaystyle \lambda ^{*}(6)=(2-{\sqrt {3}})({\sqrt {3}}-{\sqrt {2}})}$ und dieser Wert für ${\displaystyle w_{R5}}$ ist der Schlüssel:

${\displaystyle w_{R5}{\bigl [}(2-{\sqrt {3}})({\sqrt {3}}-{\sqrt {2}}){\bigr ]}={\text{g}}(150)\div {\text{g}}(6)^{5}=\cot {\bigl [}{\tfrac {1}{4}}\pi -{\tfrac {1}{4}}\operatorname {arccsc}({\tfrac {1}{4}}{\sqrt {10}}+{\tfrac {1}{4}}){\bigr ]}}$

So können direkt diese Neville-Theta-Werte hervorgebracht werden:

${\displaystyle \theta _{n}{\bigl \{}{\tfrac {2}{5}}K{\bigl [}(2-{\sqrt {3}})({\sqrt {3}}-{\sqrt {2}}){\bigr ]};(2-{\sqrt {3}})({\sqrt {3}}-{\sqrt {2}}){\bigr \}}=}$

${\displaystyle =2^{-1/2}\cot {\bigl [}{\tfrac {1}{4}}\pi -{\tfrac {1}{4}}\operatorname {arccsc}({\tfrac {1}{4}}{\sqrt {10}}+{\tfrac {1}{4}}){\bigr ]}^{1/2}\tan {\bigl [}{\tfrac {1}{8}}\pi -{\tfrac {1}{8}}\operatorname {arccsc}({\tfrac {1}{4}}{\sqrt {10}}+{\tfrac {1}{4}}){\bigr ]}^{1/10}\cot {\bigl [}{\tfrac {1}{8}}\pi +{\tfrac {1}{8}}\operatorname {arccsc}({\tfrac {1}{4}}{\sqrt {10}}+{\tfrac {1}{4}}){\bigr ]}^{3/10}}$

${\displaystyle \theta _{n}{\bigl \{}{\tfrac {4}{5}}K{\bigl [}(2-{\sqrt {3}})({\sqrt {3}}-{\sqrt {2}}){\bigr ]};(2-{\sqrt {3}})({\sqrt {3}}-{\sqrt {2}}){\bigr \}}=}$

${\displaystyle =2^{-1/2}\cot {\bigl [}{\tfrac {1}{4}}\pi -{\tfrac {1}{4}}\operatorname {arccsc}({\tfrac {1}{4}}{\sqrt {10}}+{\tfrac {1}{4}}){\bigr ]}^{1/2}\cot {\bigl [}{\tfrac {1}{8}}\pi -{\tfrac {1}{8}}\operatorname {arccsc}({\tfrac {1}{4}}{\sqrt {10}}+{\tfrac {1}{4}}){\bigr ]}^{1/10}\tan {\bigl [}{\tfrac {1}{8}}\pi +{\tfrac {1}{8}}\operatorname {arccsc}({\tfrac {1}{4}}{\sqrt {10}}+{\tfrac {1}{4}}){\bigr ]}^{3/10}}$

Während die Jacobischen Amplitudenfunktionen vollständige Additionstheoreme in sich aufweisen, besitzen die Nevilleschen Thetafunktionen nur reflexive Theoreme. Aber diese Theoreme können für die Ermittlung von Identitäten der Nevilleschen Thetafunktionen über reduzierte Webernsche Modulfunktionen verwendet werden. So lauten die exakten Reflexionstheoreme^[10] für die Nevilleschen Thetafunktionen ${\displaystyle \theta _{d}}$ und ${\displaystyle \theta _{n}}$ in Abhängigkeit vom elliptischen Modul:

${\displaystyle \theta _{d}(a+b;k)\,\theta _{d}(a-b;k)=(1-k^{2})\,\theta _{n}(a;k)^{2}\theta _{n}(b;k)^{2}+k^{2}\theta _{c}(a;k)^{2}\theta _{c}(b;k)^{2}}$

${\displaystyle (1-k^{2})\,\theta _{n}(a+b;k)\,\theta _{n}(a-b;k)=\theta _{d}(a;k)^{2}\theta _{d}(b;k)^{2}-k^{2}\theta _{c}(a;k)^{2}\theta _{c}(b;k)^{2}}$

Aus den genannten reflexiven Theoremen und den Verdopplungstheoremen können die Verdreifachungstheoreme durch sukzessive Verkettungen erzeugt werden.

Dies sind einige Verdopplungstheoreme:

${\displaystyle \theta _{c}(2x;k)=\theta _{c}(x;k)^{4}\,\theta _{n}(x;k)^{2}-\,\theta _{d}(x;k)^{2}\,\theta _{s}(x;k)^{2}}$

${\displaystyle \theta _{d}(2x;k)=(1-k^{2})\,\theta _{n}(x;k)^{4}+k^{2}\theta _{c}(x;k)^{4}}$

${\displaystyle (1-k^{2})\,\theta _{n}(2x;k)=\theta _{d}(x;k)^{4}-k^{2}\theta _{c}(x;k)^{4}}$

${\displaystyle \theta _{s}(2x;k)=2\,\theta _{c}(x;k)\theta _{d}(x;k)\theta _{n}(x;k)\theta _{s}(x;k)}$

Die Thetawerte der doppelten Maßeinträge stehen zu den Thetawerten der einfachen Maßeinträge in einer glatt Quartischen Beziehung.

Auf der Grundlage der nun genannten Verdopplungstheoreme entstehen so die Verdreifachungstheoreme.

Durch den Einsatz von ${\displaystyle a=2x}$ und ${\displaystyle b=x}$ kommen diese Formeln direkt hervor:

${\displaystyle \theta _{d}(3x;k)\,\theta _{d}(x;k)=(1-k^{2})\,\theta _{n}(2x;k)^{2}\theta _{n}(x;k)^{2}+k^{2}\theta _{c}(2x;k)^{2}\theta _{c}(x;k)^{2}}$

${\displaystyle (1-k^{2})\,\theta _{n}(3x;k)\,\theta _{n}(x;k)=\theta _{d}(2x;k)^{2}\theta _{d}(x;k)^{2}-k^{2}\theta _{c}(2x;k)^{2}\theta _{c}(x;k)^{2}}$

Gegeben sind folgende Tangentielle Rechenoperatoren:

${\displaystyle a\oplus b=\tan {\bigl [}\arctan(a)+\arctan(b){\bigr ]}={\frac {a+b}{1-ab}}}$

${\displaystyle c\ominus d=\tan {\bigl [}\arctan(c)-\arctan(d){\bigr ]}={\frac {c-d}{1+cd}}}$

Als tangentielle Differenz kann direkt nach folgendem Schema der Sinus Amplitudinis vom Drittel des vollständigen elliptischen Integrals K ermittelt werden:

${\displaystyle \operatorname {sn} {\biggl \langle }{\frac {1}{3}}K{\biggl \{}\tan {\bigl [}{\frac {1}{2}}\arctan(t^{3}){\bigr ]}{\biggr \}};\tan {\bigl [}{\frac {1}{2}}\arctan(t^{3}){\bigr ]}{\biggr \rangle }={\bigl (}\,{\sqrt {2{\sqrt {t^{4}-t^{2}+1}}-t^{2}+2}}+{\sqrt {t^{2}+1}}\,{\bigr )}\ominus 1}$

Aus diesem Wert können die anderen Werte einfach aufgebaut werden:

${\displaystyle \operatorname {cn} [{\tfrac {2}{3}}K(k);k]=1-\operatorname {sn} [{\tfrac {1}{3}}K(k);k]}$

${\displaystyle \operatorname {dn} [{\tfrac {2}{3}}K(k);k]=\operatorname {cn} [{\tfrac {2}{3}}K(k);k]\div \operatorname {sn} [{\tfrac {1}{3}}K(k);k]}$

${\displaystyle \operatorname {dn} [{\tfrac {1}{3}}K(k);k]={\sqrt {1-k^{2}}}\,\operatorname {sn} [{\tfrac {1}{3}}K(k);k]\div \operatorname {cn} [{\tfrac {2}{3}}K(k);k]}$

Für die Drittelungen und Fünftelungen des vollständigen elliptischen Integrals K werden im nun Folgenden die Identitäten in Relation zu den Jacobischen Amplitudenfunktionen und zu den reduzierten Weberschen Modulfunktionen genannt:

Diese Formeln gelten für die Dreiteilung des vollständigen elliptischen Integrals erster Art K:

${\displaystyle \theta _{d}{\bigl [}{\tfrac {1}{3}}K(k);k{\bigr ]}={\tfrac {1}{2}}{\sqrt[{12}]{1-k^{2}}}{\sqrt[{3}]{4\operatorname {dn} [{\tfrac {1}{3}}K(k);k]\operatorname {nc} [{\tfrac {2}{3}}K(k);k]}}}$

${\displaystyle \theta _{d}{\bigl [}{\tfrac {2}{3}}K(k);k{\bigr ]}={\tfrac {1}{2}}{\sqrt[{3}]{4\operatorname {ns} [{\tfrac {1}{3}}K(k);k]\operatorname {dn} [{\tfrac {2}{3}}K(k);k]}}}$

Das sind die Theoreme für die Reduzierten Weberschen Modulfunktionen von der Stufe drei:

${\displaystyle {\color {ProcessBlue}w_{R3}(\varepsilon )^{12}-2{\sqrt {2}}\,w_{R3}(\varepsilon )^{9}-\tan {\bigl [}2\arctan(\varepsilon ){\bigr ]}^{2}{\bigl [}2{\sqrt {2}}\,w_{R3}(\varepsilon )^{3}+1{\bigr ]}=0}}$

${\displaystyle {\color {RoyalBlue}W_{R3}(\varepsilon )^{12}-2{\sqrt {2}}\,W_{R3}(\varepsilon )^{9}+\sin {\bigl [}2\arcsin(\varepsilon ){\bigr ]}^{2}{\bigl [}2{\sqrt {2}}\,W_{R3}(\varepsilon )^{3}+1{\bigr ]}=0}}$

Neben den genannten Theoremen kann auch eine Parametrisierungsformel für die Ermittlung der reduzierten Weberschen Modulfunktionen herangezogen werden:

${\displaystyle w_{R3}{\bigl \{}\tan {\bigl [}{\tfrac {1}{2}}\arctan(t^{3}){\bigr ]}{\bigr \}}=2^{-1/6}\left({\sqrt {t^{2}+1}}\,{\sqrt {2{\sqrt {t^{4}-t^{2}+1}}-t^{2}+2}}+{\sqrt {t^{4}-t^{2}+1}}+1\right)^{1/3}}$

Mit den reduzierten Weberschen Modulfunktionen gilt:

${\displaystyle \theta _{n}{\bigl [}{\tfrac {2}{3}}K(k);k{\bigr ]}={\tfrac {1}{2}}{\sqrt {2}}\,w_{R3}(k)}$

${\displaystyle \theta _{d}{\bigl [}{\tfrac {2}{3}}K(k);k{\bigr ]}={\tfrac {1}{2}}{\sqrt {2}}\,W_{R3}(k)}$

Mit den Ramanujanschen Funktionen ${\displaystyle {\text{g}}}$ und ${\displaystyle {\text{G}}}$ sowie mit der Elliptischen Lambda-Stern-Funktion gelten diese Beziehungen:

${\displaystyle \theta _{n}{\bigl \{}{\tfrac {2}{3}}K{\bigl [}\lambda ^{*}(m){\bigr ]};\lambda ^{*}(m){\bigr \}}={\tfrac {1}{2}}{\sqrt {2}}\,{\text{g}}(m)^{-3}{\text{g}}(9\,m)}$

${\displaystyle \theta _{d}{\bigl \{}{\tfrac {2}{3}}K{\bigl [}\lambda ^{*}(m){\bigr ]};\lambda ^{*}(m){\bigr \}}={\tfrac {1}{2}}{\sqrt {2}}\,{\text{G}}(m)^{-3}{\text{G}}(9\,m)}$

Die Reduzierten Weberschen Funktionen ${\displaystyle w_{R5}(k)}$ und ${\displaystyle W_{R5}(k)}$ dienen zur schnellen sowie effizienten Ermittlung der Nevilleschen Thetafunktionswerte von den Fünfteln des K-Integrals:

Die Definitionen und Identitäten dieser beiden Funktionen sind in nachfolgender Tabelle zusammengefasst:

Definitionen und Identitäten von w und W

Kleine reduzierte Webersche Funktion	Große reduzierte Webersche Funktion
Pochhammersche Definitionen
${\displaystyle {\color {ProcessBlue}w_{R5}(k)={\frac {2\,[q(k)^{5};q(k)^{10}]_{\infty }}{[q(k);q(k)^{2}]_{\infty }^{5}}}}}$	${\displaystyle {\color {RoyalBlue}W_{R5}(k)={\frac {2\,[q(k)^{10};q(k)^{20}]_{\infty }\,[q(k);q(k)^{2}]_{\infty }^{5}}{[q(k)^{5};q(k)^{10}]_{\infty }\,[q(k)^{2};q(k)^{4}]_{\infty }^{5}}}}}$
Ramanujansche Definitionen
${\displaystyle {\color {ProcessBlue}w_{R5}(\varepsilon )={\frac {{\text{g}}[25K'(\varepsilon )^{2}\div K(\varepsilon )^{2}]}{{\text{g}}[K'(\varepsilon )^{2}\div K(\varepsilon )^{2}]^{5}}}}}$	${\displaystyle {\color {RoyalBlue}W_{R5}(\varepsilon )={\frac {{\text{G}}[25K'(\varepsilon )^{2}\div K(\varepsilon )^{2}]}{{\text{G}}[K'(\varepsilon )^{2}\div K(\varepsilon )^{2}]^{5}}}}}$
Jacobische Thetaformeln
${\displaystyle {\color {ProcessBlue}w_{R5}(k)={\frac {5\,\vartheta _{01}[q(k)^{5}]^{2}}{2\,\vartheta _{01}[q(k)]^{2}}}-{\frac {1}{2}}}}$	${\displaystyle {\color {RoyalBlue}W_{R5}(k)={\frac {5\,\vartheta _{00}[q(k)^{5}]^{2}}{2\,\vartheta _{00}[q(k)]^{2}}}-{\frac {1}{2}}}}$
Bilanzen der Amplitudenfunktionen
${\displaystyle {\color {ProcessBlue}w_{R5}(k)=\operatorname {nc} {\bigl [}{\tfrac {4}{5}}K(k);k{\bigr ]}-\operatorname {nc} {\bigl [}{\tfrac {2}{5}}K(k);k{\bigr ]}}}$	${\displaystyle {\color {RoyalBlue}W_{R5}(k)=\operatorname {dn} {\bigl [}{\tfrac {2}{5}}K(k);k{\bigr ]}+\operatorname {dn} {\bigl [}{\tfrac {4}{5}}K(k);k{\bigr ]}}}$

Die Funktionen ${\displaystyle {\text{g}}}$ und ${\displaystyle {\text{G}}}$ stellen die Ramanujanschen Funktionen dar.

Mit Gleichungen sechsten Grades ermittelt man die Werte der genannten Reduzierten Weberschen Modulfunktionen in Abhängigkeit vom Modul k simultan oder sukzessiv:

${\displaystyle {\color {ProcessBlue}w_{R5}(k)^{6}-2\,w_{R5}(k)^{5}}=\tan {\bigl [}2\arctan(k){\bigr ]}^{2}{\color {ProcessBlue}{\bigl [}2\,w_{R5}(k)+1{\bigr ]}}}$

${\displaystyle {\color {RoyalBlue}2\,W_{R5}(k)^{5}-W_{R5}(k)^{6}}=\sin {\bigl [}2\arcsin(k){\bigr ]}^{2}{\color {RoyalBlue}{\bigl [}2\,W_{R5}(k)+1{\bigr ]}}}$

Dieselben Gleichungen können auch weiter vereinfacht über die Tangensdifferenz mit der Zahl Zwei dargestellt werden:

${\displaystyle w_{R5}(k)\ominus 2=\tan {\bigl [}2\arctan(k){\bigr ]}^{2}w_{R5}(k)^{-5}}$

${\displaystyle 2\ominus W_{R5}(k)=\sin {\bigl [}2\arcsin(k){\bigr ]}^{2}W_{R5}(k)^{-5}}$

Von der Funktion ${\displaystyle w_{R5}}$ auf die Funktion ${\displaystyle W_{R5}}$ kann so übergeleitet werden:

${\displaystyle W_{R5}(k)=w_{R5}(k)^{-2}{\biggl \{}{\frac {1-k^{2}}{1+k^{2}}}{\bigl [}w_{R5}(k)^{2}-w_{R5}(k)-1{\bigr ]}{\bigl [}w_{R5}(k)^{2}+1{\bigr ]}+w_{R5}(k)+1{\biggr \}}}$

Direkt daraus können im Anschluss die Nevilleschen Thetafunktionswerte so ermittelt werden:

${\displaystyle \theta _{n}{\bigl [}{\tfrac {2}{5}}K(k);k{\bigr ]}=2^{-1/2}\,w_{R5}(k)^{1/2}\tan {\bigl \{}{\tfrac {1}{2}}\operatorname {arccot} {\bigl [}w_{R5}(k){\bigr ]}{\bigr \}}^{1/10}\cot {\bigl \{}{\tfrac {1}{2}}\arctan {\bigl [}w_{R5}(k){\bigr ]}{\bigr \}}^{3/10}}$

${\displaystyle \theta _{n}{\bigl [}{\tfrac {4}{5}}K(k);k{\bigr ]}=2^{-1/2}\,w_{R5}(k)^{1/2}\cot {\bigl \{}{\tfrac {1}{2}}\operatorname {arccot} {\bigl [}w_{R5}(k){\bigr ]}{\bigr \}}^{1/10}\tan {\bigl \{}{\tfrac {1}{2}}\arctan {\bigl [}w_{R5}(k){\bigr ]}{\bigr \}}^{3/10}}$

Die andere von den beiden reduzierten Weberschen Modulfunktionen liefert diese Resultate auf einfache Weise:

${\displaystyle \theta _{d}{\bigl [}{\tfrac {2}{5}}K(k);k{\bigr ]}=2^{-1/2}\,W_{R5}(k)^{1/2}\tan {\bigl \{}{\tfrac {1}{2}}\operatorname {arccot} {\bigl [}W_{R5}(k){\bigr ]}{\bigr \}}^{1/10}\cot {\bigl \{}{\tfrac {1}{2}}\arctan {\bigl [}W_{R5}(k){\bigr ]}{\bigr \}}^{3/10}}$

${\displaystyle \theta _{d}{\bigl [}{\tfrac {4}{5}}K(k);k{\bigr ]}=2^{-1/2}\,W_{R5}(k)^{1/2}\cot {\bigl \{}{\tfrac {1}{2}}\operatorname {arccot} {\bigl [}W_{R5}(k){\bigr ]}{\bigr \}}^{1/10}\tan {\bigl \{}{\tfrac {1}{2}}\arctan {\bigl [}W_{R5}(k){\bigr ]}{\bigr \}}^{3/10}}$

Folgende weitere Beziehungen führen zu den Neville-Theta-Werten aus einem Fünftel und drei Fünfteln vom Integral K:

${\displaystyle \theta _{d}{\bigl [}{\tfrac {1}{5}}K(k);k{\bigr ]}={\tfrac {1}{2}}{\sqrt[{4}]{1-k^{2}}}\,\theta _{n}{\bigl [}{\tfrac {4}{5}}K(k);k{\bigr ]}}$

${\displaystyle \theta _{d}{\bigl [}{\tfrac {3}{5}}K(k);k{\bigr ]}={\tfrac {1}{2}}{\sqrt[{4}]{1-k^{2}}}\,\theta _{n}{\bigl [}{\tfrac {2}{5}}K(k);k{\bigr ]}}$

Die folgenden Tangensdifferenzen gereichen zur Ermittlung der Amplitudenfunktionswerte:

${\displaystyle \operatorname {cn} {\bigl [}{\tfrac {2}{5}}K(\varepsilon );\varepsilon {\bigr ]}={\sqrt {2\,W_{R5}(\varepsilon )+1}}{\bigl [}{\sqrt {W_{R5}(\varepsilon )^{2}+1}}+W_{R5}(\varepsilon ){\bigr ]}\ominus 1}$

${\displaystyle \operatorname {cn} {\bigl [}{\tfrac {4}{5}}K(\varepsilon );\varepsilon {\bigr ]}=1\ominus {\sqrt {2\,W_{R5}(\varepsilon )+1}}{\bigl [}{\sqrt {W_{R5}(\varepsilon )^{2}+1}}-W_{R5}(\varepsilon ){\bigr ]}}$

Eine weitere Fortpflanzung der Amplitudenfunktionswerte erfolgt dadurch:

${\displaystyle \operatorname {sn} {\bigl [}{\tfrac {2}{5}}K(\varepsilon );\varepsilon {\bigr ]}={\sqrt {1-\operatorname {cn} {\bigl [}{\tfrac {2}{5}}K(\varepsilon );\varepsilon {\bigr ]}^{2}}}}$

${\displaystyle \operatorname {sn} {\bigl [}{\tfrac {4}{5}}K(\varepsilon );\varepsilon {\bigr ]}={\sqrt {1-\operatorname {cn} {\bigl [}{\tfrac {4}{5}}K(\varepsilon );\varepsilon {\bigr ]}^{2}}}}$

${\displaystyle \operatorname {dn} {\bigl [}{\tfrac {2}{5}}K(\varepsilon );\varepsilon {\bigr ]}={\sqrt {1-k^{2}+k^{2}\operatorname {cn} {\bigl [}{\tfrac {2}{5}}K(\varepsilon );\varepsilon {\bigr ]}^{2}}}}$

${\displaystyle \operatorname {dn} {\bigl [}{\tfrac {4}{5}}K(\varepsilon );\varepsilon {\bigr ]}={\sqrt {1-k^{2}+k^{2}\operatorname {cn} {\bigl [}{\tfrac {4}{5}}K(\varepsilon );\varepsilon {\bigr ]}^{2}}}}$

Durch Zuhilfenahme der Jacobischen Amplitudenfunktionswerte lassen sich die Nevilleschen Werte ebenso ermitteln:

${\displaystyle \theta _{d}{\bigl [}{\tfrac {1}{5}}K(k);k{\bigr ]}={\tfrac {1}{2}}{\sqrt[{4}]{1-k^{2}}}{\sqrt[{5}]{8\,w_{R5}(k)\operatorname {sn} [{\tfrac {2}{5}}K(k);k]\operatorname {ns} [{\tfrac {4}{5}}K(k);k]\operatorname {nc} [{\tfrac {4}{5}}K(k);k]\operatorname {nd} [{\tfrac {4}{5}}K(k);k]}}}$

${\displaystyle \theta _{d}{\bigl [}{\tfrac {2}{5}}K(k);k{\bigr ]}={\tfrac {1}{2}}{\sqrt[{5}]{8\,w_{R5}(k)\operatorname {sn} [{\tfrac {4}{5}}K(k);k]\operatorname {ns} [{\tfrac {2}{5}}K(k);k]\operatorname {nc} [{\tfrac {2}{5}}K(k);k]\operatorname {dn} [{\tfrac {2}{5}}K(k);k]^{4}}}}$

${\displaystyle \theta _{d}{\bigl [}{\tfrac {3}{5}}K(k);k{\bigr ]}={\tfrac {1}{2}}{\sqrt[{4}]{1-k^{2}}}{\sqrt[{5}]{8\,w_{R5}(k)\operatorname {sn} [{\tfrac {4}{5}}K(k);k]\operatorname {ns} [{\tfrac {2}{5}}K(k);k]\operatorname {nc} [{\tfrac {2}{5}}K(k);k]\operatorname {nd} [{\tfrac {2}{5}}K(k);k]}}}$

${\displaystyle \theta _{d}{\bigl [}{\tfrac {4}{5}}K(k);k{\bigr ]}={\tfrac {1}{2}}{\sqrt[{5}]{8\,w_{R5}(k)\operatorname {sn} [{\tfrac {2}{5}}K(k);k]\operatorname {ns} [{\tfrac {4}{5}}K(k);k]\operatorname {nc} [{\tfrac {4}{5}}K(k);k]\operatorname {dn} [{\tfrac {4}{5}}K(k);k]^{4}}}}$

Für die Siebenteilung gelten diese Identitäten der Nevilleschen Thetaprodukte:

${\displaystyle \theta _{n}{\bigl [}{\tfrac {2}{7}}K(k);k{\bigr ]}\theta _{n}{\bigl [}{\tfrac {4}{7}}K(k);k{\bigr ]}\theta _{n}{\bigl [}{\tfrac {6}{7}}K(k);k{\bigr ]}=2^{-3/2}w_{R7}(k)}$

${\displaystyle \theta _{d}{\bigl [}{\tfrac {2}{7}}K(k);k{\bigr ]}\theta _{d}{\bigl [}{\tfrac {4}{7}}K(k);k{\bigr ]}\theta _{d}{\bigl [}{\tfrac {6}{7}}K(k);k{\bigr ]}=2^{-3/2}W_{R7}(k)}$

Die Produkte der Werte ${\displaystyle \theta _{n}}$ und auch die Produkte der Werte ${\displaystyle \theta _{d}}$ ergeben stets die Werte w beziehungsweise W der reduzierten Weberschen Modulfunktionen:

${\displaystyle w_{R7}(k)={\frac {{\text{g}}[49K'(k)^{2}\div K(k)^{2}]}{{\text{g}}[K'(k)^{2}\div K(k)^{2}]^{7}}}}$

${\displaystyle W_{R7}(k)={\frac {{\text{G}}[49K'(k)^{2}\div K(k)^{2}]}{{\text{G}}[K'(k)^{2}\div K(k)^{2}]^{7}}}}$

Die reduzierten Weberschen Funktionen der Stufe sieben werden durch Gleichungen achten Grades gelöst:

${\displaystyle {\color {ProcessBlue}w_{R7}(\varepsilon )^{8}-2{\sqrt {2}}\,w_{R7}(\varepsilon )^{7}-7\tan {\bigl [}2\arctan(\varepsilon ){\bigr ]}^{2}w_{R7}(\varepsilon )^{4}+\tan {\bigl [}2\arctan(\varepsilon ){\bigr ]}^{4}{\bigl [}-2{\sqrt {2}}\,w_{R7}(\varepsilon )+1{\bigr ]}=0}}$

${\displaystyle {\color {RoyalBlue}W_{R7}(\varepsilon )^{8}-2{\sqrt {2}}\,W_{R7}(\varepsilon )^{7}+7\sin {\bigl [}2\arcsin(\varepsilon ){\bigr ]}^{2}W_{R7}(\varepsilon )^{4}+\sin {\bigl [}2\arcsin(\varepsilon ){\bigr ]}^{4}{\bigl [}-2{\sqrt {2}}\,W_{R7}(\varepsilon )+1{\bigr ]}=0}}$

Für die Elfteilung gelten diese Identitäten der Nevilleschen Thetaprodukte:

${\displaystyle \theta _{n}{\bigl [}{\tfrac {2}{11}}K(k);k{\bigr ]}\theta _{n}{\bigl [}{\tfrac {4}{11}}K(k);k{\bigr ]}\theta _{n}{\bigl [}{\tfrac {6}{11}}K(k);k{\bigr ]}\theta _{n}{\bigl [}{\tfrac {8}{11}}K(k);k{\bigr ]}\theta _{n}{\bigl [}{\tfrac {10}{11}}K(k);k{\bigr ]}=2^{-5/2}w_{R11}(k)}$

${\displaystyle \theta _{d}{\bigl [}{\tfrac {2}{11}}K(k);k{\bigr ]}\theta _{d}{\bigl [}{\tfrac {4}{11}}K(k);k{\bigr ]}\theta _{d}{\bigl [}{\tfrac {6}{11}}K(k);k{\bigr ]}\theta _{d}{\bigl [}{\tfrac {8}{11}}K(k);k{\bigr ]}\theta _{d}{\bigl [}{\tfrac {10}{11}}K(k);k{\bigr ]}=2^{-5/2}W_{R11}(k)}$

Analog zum vorherigen Fall gilt auch für diesen Fall das folgende Muster:

${\displaystyle w_{R11}(k)={\frac {{\text{g}}[121K'(k)^{2}\div K(k)^{2}]}{{\text{g}}[K'(k)^{2}\div K(k)^{2}]^{11}}}}$

${\displaystyle W_{R11}(k)={\frac {{\text{G}}[121K'(k)^{2}\div K(k)^{2}]}{{\text{G}}[K'(k)^{2}\div K(k)^{2}]^{11}}}}$

Die reduzierten Weberschen Funktionen der Stufe elf werden durch Gleichungen zwölften Grades gelöst:

${\displaystyle {\color {ProcessBlue}w_{R11}(\varepsilon )^{12}-\tan {\bigl [}2\arctan(\varepsilon ){\bigr ]}^{10}=2{\sqrt {2}}\,w_{R11}(\varepsilon ){\bigl \{}w_{R11}(\varepsilon )^{2}+\tan {\bigl [}2\arctan(\varepsilon ){\bigr ]}^{2}{\bigr \}}\times }}$

${\displaystyle {\color {ProcessBlue}\times {\bigl \{}w_{R11}(\varepsilon )^{4}+3\tan {\bigl [}2\arctan(\varepsilon ){\bigr ]}^{2}w_{R11}(\varepsilon )^{2}+\tan {\bigl [}2\arctan(\varepsilon ){\bigr ]}^{4}{\bigr \}}\times }}$

${\displaystyle {\color {ProcessBlue}\times {\bigl \{}2\,w_{R11}(\varepsilon )^{4}+3\tan {\bigl [}2\arctan(\varepsilon ){\bigr ]}^{2}w_{R11}(\varepsilon )^{2}+2\tan {\bigl [}2\arctan(\varepsilon ){\bigr ]}^{4}{\bigr \}}}}$

${\displaystyle {\color {RoyalBlue}W_{R11}(\varepsilon )^{12}+\sin {\bigl [}2\arcsin(\varepsilon ){\bigr ]}^{10}=2{\sqrt {2}}\,W_{R11}(\varepsilon ){\bigl \{}W_{R11}(\varepsilon )^{2}-\sin {\bigl [}2\arcsin(\varepsilon ){\bigr ]}^{2}{\bigr \}}\times }}$

${\displaystyle {\color {RoyalBlue}\times {\bigl \{}W_{R11}(\varepsilon )^{4}-3\sin {\bigl [}2\arcsin(\varepsilon ){\bigr ]}^{2}W_{R11}(\varepsilon )^{2}+\sin {\bigl [}2\arcsin(\varepsilon ){\bigr ]}^{4}{\bigr \}}\times }}$

${\displaystyle {\color {RoyalBlue}\times {\bigl \{}2\,W_{R11}(\varepsilon )^{4}-3\sin {\bigl [}2\arcsin(\varepsilon ){\bigr ]}^{2}W_{R11}(\varepsilon )^{2}+2\sin {\bigl [}2\arcsin(\varepsilon ){\bigr ]}^{4}{\bigr \}}}}$

Genau dann, wenn der Webersche Funktionsindex in Form einer ungerade Zahl größer als Eins eine Primzahl ist, hat die korrespondierende Gleichung mit dem reduzierten Weberschen Funktionswert als Lösung der Gleichung einen Grad gleich dem Nachfolger des Funktionsindex.

Alle Jacobischen Amplitudenfunktionen können nach folgendem Schema direkt erzeugt werden:

${\displaystyle \operatorname {pq} (u;k)={\frac {\theta _{p}(u;k)}{\theta _{q}(u;k)}}}$

Hierbei stehen die Buchstaben ${\displaystyle p}$ und ${\displaystyle q}$ stellvertretend für die Buchstaben ${\displaystyle c}$, ${\displaystyle d}$, ${\displaystyle n}$ und ${\displaystyle s}$ und so dient diese Formel für die Erstellung der gesamten Gruppe aller Jacobischen Elliptischen Funktionen der Standard-Amplitudenform!

Beispielsweise gelten für den Sinus Amplitudinis und seine um das K-Integral horizontal verschobene Funktion folgende Quotienten:

${\displaystyle \operatorname {sn} (u;k)={\frac {\theta _{s}(u;k)}{\theta _{n}(u;k)}}}$

${\displaystyle \operatorname {cd} (u;k)={\frac {\theta _{c}(u;k)}{\theta _{d}(u;k)}}}$

Während die Nevilleschen Thetafunktionen nur Reflexionstheoreme in sich aufweisen, besitzen die sich als Quotienten der Nevilleschen Funktionen ergebenden Jacobischen Amplitudenfunktionen sogar vollständige Additionstheoreme:

${\displaystyle \operatorname {sn} (x+y;k)={\frac {\operatorname {sn} (x;k)\operatorname {cd} (y;k)+\operatorname {cd} (x;k)\operatorname {sn} (y;k)}{1+k^{2}\operatorname {sn} (x;k)\operatorname {cd} (x;k)\operatorname {sn} (y;k)\operatorname {cd} (y;k)}}}$

${\displaystyle \operatorname {cd} (x+y;k)={\frac {\operatorname {cd} (x;k)\operatorname {cd} (y;k)-\operatorname {sn} (x;k)\operatorname {sn} (y;k)}{1-k^{2}\operatorname {sn} (x;k)\operatorname {cd} (x;k)\operatorname {sn} (y;k)\operatorname {cd} (y;k)}}}$

Die Ableitungen der Nevilleschen Thetafunktionen lassen sich vereinfacht mit Hilfe der Jacobischen Zetafunktion ${\displaystyle \mathrm {zn} }$ darstellen.

Das Zeta Ampitudinis ist so definiert:

${\displaystyle {\text{zn}}(z;k)=E[{\text{am}}(z;k);k]-{\frac {E(k)z}{K(k)}}}$

${\displaystyle {\text{zn}}(z;k)=\sum _{n=1}^{\infty }{\frac {4\sin {\bigl [}2\,z\div {\bar {K}}(k){\bigr ]}q(k)^{2n-1}}{{\bar {K}}(k){\bigl \{}1-2\cos {\bigl [}2\,z\div {\bar {K}}(k){\bigr ]}q(k)^{2n-1}+q(k)^{4n-2}{\bigr \}}}}}$

So werden die ersten Ableitungen beziehungsweise Differentialquotienten ermittelt:

${\displaystyle {\frac {\partial }{\partial \,x}}\,\theta _{n}(x;k)=\theta _{n}(x;k)\,\mathrm {zn} (x;k)}$

${\displaystyle {\frac {\partial }{\partial \,x}}\,\theta _{d}(x;k)=\theta _{d}(x;k){\bigl [}\mathrm {zn} (x;k)-k^{2}\mathrm {sn} (x;k)\,\mathrm {cd} (x;k){\bigr ]}}$

${\displaystyle {\frac {\partial }{\partial \,x}}\,\theta _{c}(x;k)=\theta _{c}(x;k){\bigl [}\mathrm {zn} (x;k)-\mathrm {sn} (x;k)\,\mathrm {dc} (x;k){\bigr ]}}$

Die gerade eben genannte Formel kann auch als sogenannte Logarithmische Ableitung dargestellt werden:

${\displaystyle {\frac {\partial }{\partial \,x}}\ln {\bigl [}\theta _{n}(x;k){\bigr ]}=\mathrm {zn} (x;k)}$

Das war die zuvor erwähnte Formel für das Zeta Amplitudinis:

${\displaystyle \mathrm {zn} (x;k)=\sum _{n=1}^{\infty }{\frac {4\sin[2\,x\div {\bar {K}}(k)]q(k)^{2n-1}}{{\bar {K}}(k){\bigl \{}1-2\cos[2\,x\div {\bar {K}}(k)]q(k)^{2n-1}+q(k)^{4n-2}{\bigr \}}}}}$

Mit dem Einsetzungsverfahren kommt diese Formel hervor:

${\displaystyle {\frac {\partial }{\partial \,x}}\ln {\bigl [}\theta _{n}(x;k){\bigr ]}=\sum _{n=1}^{\infty }{\frac {4\sin[2\,x\div {\bar {K}}(k)]q(k)^{2n-1}}{{\bar {K}}(k){\bigl \{}1-2\cos[2\,x\div {\bar {K}}(k)]q(k)^{2n-1}+q(k)^{4n-2}{\bigr \}}}}}$

Auf den Logarithmus Naturalis von der Nevilleschen Theta-n-Funktion gelangt man somit durch Bildung der Ursprungsstammfunktion bezüglich x:

${\displaystyle \ln {\bigl [}\theta _{n}(x;k){\bigr ]}=\sum _{n=1}^{\infty }{\biggl \langle }\ln {\bigl \{}1-2\cos {\bigl [}2\,x\div {\bar {K}}(k){\bigr ]}q(k)^{2n-1}+q(k)^{4n-2}{\bigr \}}-2\ln {\bigl [}1-q(k)^{2n-1}{\bigr ]}{\biggr \rangle }}$

${\displaystyle \ln {\bigl [}\theta _{n}(x;k){\bigr ]}=\sum _{n=1}^{\infty }\,\ln {\biggl \{}{\frac {1-2\cos[2\,x\div {\bar {K}}(k)]q(k)^{2n-1}+q(k)^{4n-2}}{[1-q(k)^{2n-1}]^{2}}}{\biggr \}}}$

Der nun genannte Ausdruck wird nun der Exponentialfunktion als äußere Funktion anvertraut:

${\displaystyle \theta _{n}(x;k)=\exp {\biggl \langle }\sum _{n=1}^{\infty }\,\ln {\biggl \{}{\frac {1-2\cos[2\,x\div {\bar {K}}(k)]q(k)^{2n-1}+q(k)^{4n-2}}{[1-q(k)^{2n-1}]^{2}}}{\biggr \}}{\biggr \rangle }}$

Der Exponentialfunktionswert aus der Summe ist gleich dem Produkt der Exponentialfunktionswerte:

${\displaystyle \theta _{n}(x;k)=\prod _{n=1}^{\infty }{\frac {1-2\cos[2\,x\div {\bar {K}}(k)]q(k)^{2n-1}+q(k)^{4n-2}}{[1-q(k)^{2n-1}]^{2}}}}$

QUOD ERAT DEMONSTRANDUM

So werden dementsprechend die zweiten Ableitungen ermittelt:

${\displaystyle {\frac {\partial ^{2}}{\partial \,x^{2}}}\,\theta _{n}(x;k)=\theta _{n}(x;k){\bigl [}\mathrm {zn} (x;k)^{2}+\mathrm {dn} (x;k)^{2}-E(k)\div K(k){\bigr ]}}$

${\displaystyle {\frac {\partial ^{2}}{\partial \,x^{2}}}\,\theta _{d}(x;k)=\theta _{d}(x;k){\bigl \{}{\bigl [}\mathrm {zn} (x;k)-k^{2}\mathrm {sn} (x;k)\,\mathrm {cd} (x;k){\bigr ]}^{2}+(1-k^{2})\,\mathrm {nd} (x;k)^{2}-E(k)\div K(k){\bigr \}}}$

${\displaystyle {\frac {\partial ^{2}}{\partial \,x^{2}}}\,\theta _{c}(x;k)=\theta _{c}(x;k){\bigl \{}{\bigl [}\mathrm {zn} (x;k)-\mathrm {sn} (x;k)\,\mathrm {dc} (x;k){\bigr ]}^{2}-(1-k^{2})\,\mathrm {sc} (x;k)^{2}-E(k)\div K(k){\bigr \}}}$

Die bestimmten Integrale von Null bis zum K-Wert ergeben folgende Resultate:

${\displaystyle \int _{0}^{K(k)}\theta _{d}(x;k)\,\mathrm {d} x={\biggl [}{\frac {\pi }{2}}\,K(k){\biggr ]}^{1/2}={\frac {\pi }{2}}\,{\bar {K}}(k)^{1/2}}$

${\displaystyle \int _{0}^{K(k)}\theta _{n}(x;k)\,\mathrm {d} x={\biggl [}{\frac {\pi }{2k'}}\,K(k){\biggr ]}^{1/2}={\frac {\pi }{2}}(1-k^{2})^{-1/4}\,{\bar {K}}(k)^{1/2}}$

• ${\displaystyle \theta _{c}(z;k)=\theta _{c}(-z;k)}$
• ${\displaystyle \theta _{d}(z;k)=\theta _{d}(-z;k)}$
• ${\displaystyle \theta _{n}(z;k)=\theta _{n}(-z;k)}$
• ${\displaystyle \theta _{s}(z;K)=-\theta _{s}(-z;k)}$

Die nun folgenden 3D-Schemata stellen den reellen Anteil und den imaginären Anteil der Nevilleschen Thetafunktionen zueinander gegenüber:

NevilleThetaC[z,m], NevilleThetaD[z,m], NevilleThetaN[z,m], and NevilleThetaS[z,m] sind hierbei die eingebaute Funktionen von Wolfram Mathematica^[11] und der rechte Klammerabschnitt enthält das Quadrat der numerischen Exzentrizität ${\displaystyle m=k^{2}}$ beziehungsweise das Quadrat des Moduls bei den Wolfram-Eingabebefehlen.

Die allgemeine Summenreihe aus Potenzen als Summanden mit konstanter Basis bezüglich des Summenindex und Exponenten in quadratischer Relation zum Summenindex lässt sich generell auf folgende Weise berechnen:

${\displaystyle \sum _{n=-\infty }^{\infty }Q^{(n+R)^{2}}={\frac {\vartheta _{00}(Q)}{\vartheta _{00}(Q')}}\,\vartheta _{00}{\bigl (}\pi \,R\,;Q'{\bigr )}=\vartheta _{00}(Q)\,\theta _{d}{\bigl \{}2\,R\,K{\bigl [}\psi _{H}(Q)^{4}{\bigr ]};\psi _{H}(Q)^{4}{\bigr \}}}$

${\displaystyle Q'=\exp {\bigl [}\pi ^{2}\div \ln(Q){\bigr ]}}$

Dabei stellt das Kürzel ${\displaystyle \psi _{H}}$ die Hermitesche elliptische Psifunktion dar:

${\displaystyle \psi _{H}(w)=\vartheta _{01}(w)^{1/2}\vartheta _{00}(w)^{-1/2}}$

${\displaystyle \psi _{H}(w)=\vartheta _{01}(w)\,\vartheta _{01}(w^{2})^{-1}}$

Für den Nevilleschen Ausdruck werden im Folgenden zwei Beispiele angeführt:

${\displaystyle \sum _{n=-\infty }^{\infty }{\bigl (}{\frac {1}{2}}{\bigr )}^{(n+1/3)^{2}}=\vartheta _{00}{\bigl (}{\frac {1}{2}}{\bigr )}\theta _{d}{\bigl \{}{\frac {2}{3}}K{\bigl [}\psi _{H}{\bigl (}{\frac {1}{2}}{\bigr )}^{4}{\bigr ]};\psi _{H}{\bigl (}{\frac {1}{2}}{\bigr )}^{4}{\bigr \}}}$

${\displaystyle \sum _{n=-\infty }^{\infty }{\bigl (}{\frac {2}{3}}{\bigr )}^{(n+2/5)^{2}}=\vartheta _{00}{\bigl (}{\frac {2}{3}}{\bigr )}\theta _{d}{\bigl \{}{\frac {4}{5}}K{\bigl [}\psi _{H}{\bigl (}{\frac {2}{3}}{\bigr )}^{4}{\bigr ]};\psi _{H}{\bigl (}{\frac {2}{3}}{\bigr )}^{4}{\bigr \}}}$

• E. H. (Eric Harold) Neville: Jacobian Elliptic Functions. Oxford Clarendon Press, 1944 (englisch, archive.org). 
• Eric W. Weisstein: Neville Theta Functions. In: MathWorld (englisch).

1. ↑ Eric Harold Neville: Jacobian Elliptic Functions. S. 274, abgerufen am 18. August 2025 (englisch). 
2. ↑ Abramowitz/Stegun: Handbook of Mathematical Functions. S. 578, abgerufen am 18. August 2025 (englisch). 
3. ↑ Abramowitz/Stegun: Handbook of Mathematical Functions. S. 578, abgerufen am 15. August 2025 (englisch, Formeln 16.36.6 und 16.36.7, Bezeichnungen angepasst). 
4. ↑ Eric W. Weisstein: Jacobi Theta Functions. In: MathWorld (englisch).
5. ↑ http://wayback.cecm.sfu.ca/~pborwein/TEMP_PROTECTED/pi-agm.pdf
6. ↑ DLMF: 20.5 Infinite Products and Related Results. Abgerufen am 13. August 2022. 
7. ↑ Neville (1944)
8. ↑ The Mathematical Functions Site
9. ↑ The Mathematical Functions Site
10. ↑ DLMF: 20.7 Identities. Abgerufen am 13. August 2022. 
11. ↑ Neville theta function: Primary definition. Abgerufen im 1. Januar 1 (englisch).