Hookesches Gesetz

Das hookesche Gesetz (nach Robert Hooke, der es 1676 als Anagramm^[1] und 1678 aufgelöst publizierte^[2]) ist das Stoffgesetz oder Materialmodell für die lineare elastische Verformung von Festkörpern (linear-elastisches Verhalten).

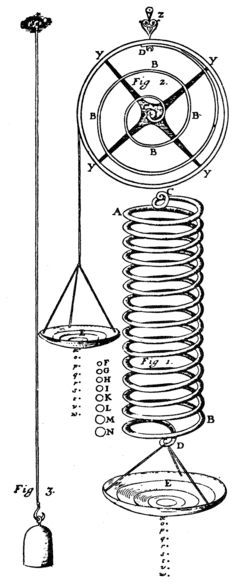
Im eindimensionalen Fall ist in diesem Modell wie bei der von Hooke untersuchten Feder im Bild die Verformung proportional zur einwirkenden Belastung. Jeder Werkstoff,^[3]:272 auch Beton oder Keramik, besitzt eine Elastizitätsgrenze, innerhalb derer er sich elastisch verhält: Unter einer einwirkenden Kraft verändert er seine Form und bei Wegfall dieser Kraft kehrt er in die Ursprungsform zurück, so wie die Feder. Gummi kann sich auch nicht-linear elastisch verhalten; bei hinreichend kleinen Verzerrungen (in erster Ordnung) verhält sich jedoch jedes isotrope Material − auch Gummi − gemäß dem hookeschen Gesetz linear elastisch.^[3]:365 Die Navier-Cauchy-Gleichungen sind die Bewegungs­gleichungen für linear-elastisch verformende Körper.

Nicht-lineares Verhalten wie plastische Verformung kündigt oft Materialversagen an, das es im Maschinenbau und Bauwesen zu vermeiden gilt. Das hookesche Gesetz findet deshalb breite Anwendung in der Festigkeitslehre und auch in der linear-elastischen Bruchmechanik. In rheologischen Modellen wird das Gesetz durch das Hooke-Element repräsentiert.

Im Jahr 1676 veröffentlichte Robert Hooke in einem Postskriptum seiner Arbeit „A description of helioscopes, and some other instruments“^[1] seine Erfindung über „Die wahre Theorie der Elastizitat oder Federkraft“ in Form des Anagramms „ceiiinosssttuv.“ Im 1678 erschienenen Werk „De Potentia Restitutiva, or of Spring Explaining the Power of Springing Bodies“^[2] verriet er den Sinn des Anagramms: Ut tensio sic vis, lateinisch Die Kraft [jeder Feder] verhält sich wie ihre Auslenkung. Hooke untersuchte dabei Spiralfedern, wie im einleitenden Bild, oder verbiegende Holzstücke. Er unterschied schon Zug-, Druck- und Biege­beanspruchung und sprach indirekt schon die Existenz der neutralen Faser aus. Er behandelte als erster die harmonische Schwingung von Massen, die durch Federn bewegt werden, und erkannte die dabei − infolge der Linearisierung − auftretende Isochronie.

Ohne Hooke zu erwähnen, haben Gottfried Wilhelm Leibniz 1684 und Edme Mariotte 1686 ebenfalls lineare Elastizität bei der Balkenbiegung verwendet, und erst ab Mitte des 19. Jahrhunderts wurde Hooke die Urheberschaft für die lineare Elastizitäts­beziehung zugesprochen.

Heute wird unter dem hookeschen Gesetz der lineare Zusammenhang zwischen mechanischer Spannung σ und Dehnung Δl/l wie beispielsweise im einachsigen Zugversuch gemäß^{[4]:356 ff.}

Δl/l = σ/E

verstanden. Die Spannung wurde erst 1755 von Leonhard Euler (in der Hydromechanik in Form des Drucks^[4]:253) und der Elastizitätsmodul E von Claude Louis Marie Henri Navier um das Jahr 1826 eingeführt,^[4]:392 also über 80 Jahre nach Hooke’s Arbeiten. Die kontinuums­mechanische Formulierung mittels Tensoren initiierte Augustin-Louis Cauchy im Jahr 1822.^[4]:395

Die molekulare Theorie von Poisson und Cauchy sagt voraus, dass lediglich ein Parameter genügt, um isotrope linear elastische Materialien zu beschreiben, genauer dass die ersten beiden Lamé-Konstanten identisch sind, was eine Poissonzahl ν=¼ erzwingt. G. Wertheim konnte jedoch 1848 experimentell zeigen, dass für einige isotrope Materialien ν≠¼ ist, sodass zwei Parameter gebraucht werden, um solche Materialien darzustellen.^[5]:96f

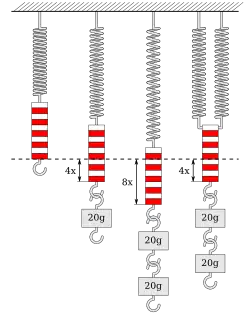
Hooke beobachtete, dass die Auslenkung Δl (~x im Bild) einer Feder linear von der wirkenden Kraft F abhängt. Bei den Schraubenfedern im Bild zeigt sich das lineare Verhalten bei Belastung mit einem Gewicht. Nach Verdoppelung des Gewichts tritt auch eine doppelte Längenänderung auf. Heute wird das als Formel folgendermaßen ausgedrückt:

${\displaystyle {\mathsf {F=D\cdot \Delta l}}}$ beziehungsweise ${\displaystyle {\mathsf {\Delta l={\frac {F}{D}}}}}$

Der Proportionalitätsfaktor D verkörpert die Federsteifigkeit.

Diese Eigenschaft ist maßgeblich zum Beispiel für die Verwendung von Metallfedern als Kraftmesser und in Waagen. Bei anderen Materialien – wie zum Beispiel Gummi – kann der Zusammenhang zwischen einwirkender Kraft und Ausdehnung nicht-linear sein.

Das hookesche Gesetz findet nicht nur in der Mechanik, sondern auch in anderen Bereichen der Physik Anwendung. In der Quantenmechanik etwa lässt sich für hinreichend kleine Δl über die Anwendung des hookeschen Gesetzes der quantenmechanische harmonische Oszillator beschreiben. Ein weiteres Beispiel ist die Molekularphysik. Hier kann, analog zur Federkonstanten, die Linearität zu Δl durch eine Kraftkonstante ausgedrückt werden. Diese Kraftkonstante beschreibt dann die Stärke einer chemischen Bindung.

Die in einer Feder durch Dehnung entstehende Formänderungsenergie wird folgendermaßen berechnet. Die Feder wird durch eine äußere Kraft F um x≷0 aus der Ruhelage (Gleichgewichtslage) bei x=0 ausgelenkt. Die Auslenkung ist proportional zur äußeren Kraft, F=D·x, und die innere Rückstellkraft F_r =−D·x ist dieser entgegen­gerichtet. Die Rückstell­kraft verrichtet entlang der Verschiebung 0→x die innere Arbeit^[6]:55f

${\displaystyle {\mathsf {W_{i}:=\int \limits _{0}^{x}F'_{r}\,\mathrm {d} x'=-\int \limits _{0}^{x}D\,x'\,\mathrm {d} x'=-\left[D\,{\frac {{x'}^{2}}{2}}\right]_{0}^{x}=-{\frac {D}{2}}\,x^{2}}}}$

Diese innere Arbeit wird nach Entlastung vollständig zurückgewonnen, womit sich die Rückstellkraft als konservative Kraft herausstellt. Die verrichtete Arbeit war in der Feder gespeichert, und eine Arbeit mit dieser besonderen Eigenschaft wird bis auf ein aus formalen Gründen noch zu berücksich­tigendes Minuszeichen als potenzielle Energie E_pot oder Potenzial V bezeichnet, hier als die Formänderungs­energie

${\displaystyle {\mathsf {W=-W_{i}={\frac {D}{2}}\,x^{2}}}}$

Dies ist das für viele Modellrechnungen wichtige harmonische Potenzial (proportional zu x²).

Auf einen schlanken, homogenen, geraden Stab der Länge l₀ und konstanter Querschnittsfläche A wirkt eine Kraft F entlang der Stabachse. Die Störung des Spannungs- und Verzerrungszustandes im Einspann- und Krafteinleitungsbereich kann nach dem Prinzip von St. Venant beim schlanken Stab vernachlässigt werden. Bezogen auf die Querschnittsfläche ergibt sich die mechanische Spannung^[6]:19

${\displaystyle {\mathsf {\sigma ={\frac {F}{A}}}}}$

in jedem Teilchen auf einer Querschnittsfläche senkrecht zur Stabachse. Der Stab wird durch die Kraft auf die Länge ${\displaystyle \ell }$ gestreckt oder gestaucht, was die Dehnung

${\displaystyle {\mathsf {\varepsilon :={\frac {\ell -l_{0}}{l_{0}}}=:{\frac {\Delta l}{l_{0}}}}}}$

definiert. Im homogenen Stab wird bei hinreichend langsamer Verformung jedes seiner Volumenelemente dieselbe Dehnung in Stabrichtung erfahren. Es zeigt sich, dass das Material des Stabes – wie jedes andere feste Material auch – im Spannungs-Dehnungs-Diagramm in der Nähe des Ursprungs eine lineare Kennlinie besitzt, deren Steigung der Elastizitätsmodul ist:

${\displaystyle {\mathsf {E:={\frac {\sigma }{\varepsilon }}\quad \rightarrow \quad \sigma =E\cdot \varepsilon }}}$

Letzteres wird in der Technischen Mechanik Hookesches Gesetz genannt (gelegentlich mit dem Zusatz „im eindimensionalen Fall“).^[7][8]

Einsetzen der ersten beiden Formeln in die letzte und Umstellen ergibt obiges #Hookesches Gesetz für Federsysteme

${\displaystyle {\mathsf {F=\underbrace {\mathsf {\frac {E\cdot A}{l_{0}}}} _{D}\cdot \Delta l=D\cdot \Delta l}}}$

ist aber beim schlanken Stab auf kleine Dehnungen (<3−8 %) beschränkt, siehe #Anwendungsbereiche und Limitierungen. Bei größeren Dehnungen würde sich hier die Änderung der Querschnittsfläche des Stabes bemerkbar machen, was ein geometrisch nicht-linearer Effekt ist. Das hookesche Gesetz für elastische Materialien ist auch bei mehrachsigen Belastungen sowie Superpositionen hiervon anwendbar und ist eine Verallgemeinerung des hookeschen Gesetzes für Federn.

Im allgemeinen Fall wird das hookesche Gesetz durch eine lineare Tensor­gleichung (4. Stufe) ausgedrückt, siehe #Elastizitätstensor:

σ = ℂ ε bzw. kartesisch σ_ij = C_ijkl ε_kl

mit dem Spannungstensor σ und dem Verzerrungstensor ε, die in einem kartesischen Koordinaten­system durch 3×3-Matrizen mit neun Koeffizienten σ_ij bzw. ε_kl dargestellt werden können. In der kartesischen Schreibweise wird die Einsteinsche Summenkonvention benutzt und über k und l von eins bis drei summiert. Der Elastizitätstensor ℂ repräsentiert die elastischen Eigenschaften der deformierbaren Materie und weist 81 Komponenten C_ijkl auf, weil die Indizes alle Werte von eins bis drei annehmen, und ist daher schwierig zu handhaben. Der Spannungs- und der Verzerrungstensor sind symmetrisch und besitzen nur sechs unabhängige Komponenten, sodass C_ijkl=C_ijlk und C_ijkl=C_jikl gesetzt werden kann und nur noch 36 Koeffizienten benötigt werden. Aus thermodynamischen Überlegungen ergibt sich, dass auch C_ijkl=C_klij, siehe Sätze über Hyperelastizität. Die Anzahl der unabhängigen Konstanten C_ijkl reduziert sich damit weiter auf maximal 21.

Die Voigtsche Notation überführt das hookesche Gesetz in eine einfacher zu handhabende Matrizengleichung, in der die elastischen Konstanten in einer symmetrischen 6×6-Matrix und die Verzerrungen und Spannungen in sechskomponentige Spaltenvektoren eingelagert werden:

${\displaystyle {\begin{bmatrix}\sigma _{1}\\\sigma _{2}\\\sigma _{3}\\\sigma _{4}\\\sigma _{5}\\\sigma _{6}\end{bmatrix}}={\begin{bmatrix}{\mathsf {C}}_{11}&{\mathsf {C}}_{12}&{\mathsf {C}}_{13}&{\mathsf {C}}_{14}&{\mathsf {C}}_{15}&{\mathsf {C}}_{16}\\&{\mathsf {C}}_{22}&{\mathsf {C}}_{23}&{\mathsf {C}}_{24}&{\mathsf {C}}_{25}&{\mathsf {C}}_{26}\\&&{\mathsf {C}}_{33}&{\mathsf {C}}_{34}&{\mathsf {C}}_{35}&{\mathsf {C}}_{36}\\&&&{\mathsf {C}}_{44}&{\mathsf {C}}_{45}&{\mathsf {C}}_{46}\\&{\text{sym.}}&&&{\mathsf {C}}_{55}&{\mathsf {C}}_{56}\\&&&&&{\mathsf {C}}_{66}\end{bmatrix}}{\begin{bmatrix}\varepsilon _{1}\\\varepsilon _{2}\\\varepsilon _{3}\\\varepsilon _{4}\\\varepsilon _{5}\\\varepsilon _{6}\end{bmatrix}}}$

Hier wurde anhand des Schemas 11 → 1, 22 → 2, 33 → 3, 23 → 4, 31 → 5, 12 → 6 die Anzahl der Indizes halbiert. Damit das Skalarprodukt der Spaltenvektoren für die Verzerrungen und Spannungen gleich dem der entsprechenden Tensoren ist, sind die Einträge ε_4,5,6 Gleitungen, d. h.

ε₄ = 2 ε₂₃, ε₅ = 2 ε₃₁, ε₆ = 2 ε₁₂

Aufgrund der Tatsache, dass anisotrope Körper in der Realität meist kristallin sind und nur eine beschränkte Anzahl Kristallgitter bekannt sind, können real existierende elastische Materialien in 13 Gruppen eingeteilt werden:^[3]

1. Isotropie mit zwei Konstanten wie hier dargestellt,
2. Trikline Anisotropie mit 21 Konstanten,
3. Monokline Anisotropie mit 13 Konstanten,
4. Orthotropie mit neun Konstanten,
5. Tetragonale Anisotropie in zwei Varianten mit sechs bzw. sieben Konstanten,
7. Kubische Anisotropie in zwei Varianten mit drei Konstanten,
9. Hexagonale Anisotropie in vier Varianten mit fünf bis sieben Konstanten und
13. Transversale Isotropie mit fünf Konstanten.

Die linear elastische Feder findet breite Anwendung in der Schwingungslehre und damit in der Modalanalyse, Starrkörpersimulation und verwandten Disziplinen. Wie in der Einleitung bereits mitgeteilt wird das hookesche Gesetz in der Festigkeitslehre benutzt, insbesondere in den Energiemethoden wie dem Satz von Castigliano oder dem Satz von Betti. Die Strukturmechanik wendet es in der Balken-, Scheiben-, Platten- und Schalentheorie an. Spannungsfunktionen wie die Airysche Spannungsfunktion basieren auf dem hookeschen Gesetz.

Das hookesche Gesetz gilt nur innerhalb der Elastizitätsgrenze, solange die Federn nicht überdehnt werden, das Material nicht plastisch fließt oder bricht. Die Elastizitätsgrenze von Stählen und die Bruchdehnung von Keramiken liegen unterhalb von 1 % Dehnung.^[9] Geschwindigkeits­abhängiges Materialverhalten wie Kriechen wird ebenfalls nicht abgebildet.

Die klassische Theorie für den linear-elastischen Festkörper, wie sie im technischen Bereich noch heute angewendet und hier dargestellt wird, gilt nur im geometrisch linearen Bereich mit Verzerrungen, die klein gegen eins sind (<3−8 %, darüber machen sich geometrisch nicht-lineare Effekte bemerkbar). Ein hiermit vermiedenes Problem zeigt sich beim Stab im Abschnitt #Eindimensionaler Fall. Denn die Dehnung ${\displaystyle \varepsilon :={\tfrac {\ell -l_{0}}{l_{0}}}}$ ist bei Kompression auf die Länge ${\displaystyle \ell =0}$ gleich ${\displaystyle \varepsilon ={\tfrac {0-l_{0}}{l_{0}}}=-1}$ und die Spannung σ=E·ε=−E ist endlich, was beim zusammen­gepressten Stab physikalisch unsinnig ist.

Auch die #Erweiterung auf große Deformationen liefert nur bei moderaten Deformationen physikalisch plausible Antworten, siehe die Beispielrechnung im Artikel Kontinuumsmechanik. Die eindeutige Lösbarkeit von Randwertaufgaben, in denen elastische Körper vorkommen, erfordert, dass deren Formänderungsenergie eine koerzitive polykonvexe Funktion ist.^[10] Dies hätte zur Folge, dass das Zusammenpressen eines Stabes auf Nulllänge unendlich große Spannungen verlangen würde, was das hookesche Gesetz nicht hergibt. Mögliche Abhilfen für dieses Problem sind bei Polykonvexe Funktion nachzuschlagen.

Im Spezialfall isotroper linear elastischer Medien werden nur zwei elastische Konstanten gebraucht, um die #Matrizengleichung aufzuschreiben. Mit den Lamé-Konstanten λ und μ, die beide vom Werkstoff bestimmt sind, lautet sie:

${\displaystyle {\begin{bmatrix}\sigma _{1}\\\sigma _{2}\\\sigma _{3}\\\sigma _{4}\\\sigma _{5}\\\sigma _{6}\end{bmatrix}}={\begin{bmatrix}\lambda +2\,\mu &\lambda &\lambda &0&0&0\\\lambda &\lambda +2\,\mu &\lambda &0&0&0\\\lambda &\lambda &\lambda +2\,\mu &0&0&0\\0&0&0&\mu &0&0\\0&0&0&0&\mu &0\\0&0&0&0&0&\mu \end{bmatrix}}{\begin{bmatrix}\varepsilon _{1}\\\varepsilon _{2}\\\varepsilon _{3}\\\varepsilon _{4}\\\varepsilon _{5}\\\varepsilon _{6}\end{bmatrix}}}$

In der Technischen Mechanik werden oft stattdessen der Elastizitätsmodul E (englisch Young’s modulus) und die Querkontraktions­zahl ν (englisch Poisson’s ratio) benutzt, die daher auch Ingenieurskonstanten genannt werden.^[5]:96 Mit

${\displaystyle \lambda ={\frac {E\,\nu }{(1+\nu )(1-2\,\nu )}},\quad \mu ={\frac {E}{2(1+\nu )}}}$

entsteht

${\displaystyle {\begin{bmatrix}\sigma _{1}\\\sigma _{2}\\\sigma _{3}\\\sigma _{4}\\\sigma _{5}\\\sigma _{6}\end{bmatrix}}={\frac {E}{(1+\nu )(1-2\nu )}}{\begin{bmatrix}1-\nu &\nu &\nu &0&0&0\\&1-\nu &\nu &0&0&0\\&&1-\nu &0&0&0\\&&&{\frac {1-2\nu }{2}}&0&0\\&{\text{sym.}}&&&{\frac {1-2\nu }{2}}&0\\&&&&&{\frac {1-2\nu }{2}}\end{bmatrix}}{\begin{bmatrix}\varepsilon _{1}\\\varepsilon _{2}\\\varepsilon _{3}\\\varepsilon _{4}\\\varepsilon _{5}\\\varepsilon _{6}\end{bmatrix}}}$

Die umgekehrte Relation lautet

${\displaystyle {\begin{bmatrix}\varepsilon _{1}\\\varepsilon _{2}\\\varepsilon _{3}\\\varepsilon _{4}\\\varepsilon _{5}\\\varepsilon _{6}\end{bmatrix}}={\frac {1}{E}}{\begin{bmatrix}1&-\nu &-\nu &0&0&0\\&1&-\nu &0&0&0\\&&1&0&0&0\\&&&2(1+\nu )&0&0\\&{\text{sym.}}&&&2(1+\nu )&0\\&&&&&2(1+\nu )\end{bmatrix}}{\begin{bmatrix}\sigma _{1}\\\sigma _{2}\\\sigma _{3}\\\sigma _{4}\\\sigma _{5}\\\sigma _{6}\end{bmatrix}}}$.

Materialversuche dienen der Identifikation der Materialparameter und werden so ausgelegt, dass die Materialparameter klar zu Tage treten. Bei drei speziellen Belastungen

1. Zugversuch,
2. Torsion und
3. allseitiger Druck

stellen sich quasi eindimensionale Verhältnisse ein, sodass die elastischen Konstanten leicht zu ermitteln sind.

Zugversuch

Bei Zug in 1-Richtung ist ${\displaystyle \sigma _{1}\neq 0,\sigma _{2,\dots ,6}=0}$ und daher^[5]:96

${\displaystyle \varepsilon _{1}={\frac {1}{E}}\sigma _{1},\;\varepsilon _{2}=\varepsilon _{3}=-{\frac {\nu }{E}}\sigma _{1}=-\nu \varepsilon _{1},\;\varepsilon _{4,5,6}=0}$

siehe auch #Eindimensionaler Fall.

Torsion

Im Kreiszylinder mit Achse in 3-Richtung tritt hier reine Scherung in der 12-Ebene auf, sodass nur die 6-Komponenten besetzt sind und nur eine aussagekräftige Gleichung übrig bleibt:

${\displaystyle \sigma _{6}={\frac {E}{2(1+\nu )}}\,\varepsilon _{6}=G\,\varepsilon _{6},\quad G:={\frac {E}{2(1+\nu )}}}$

Darin ist G der Schubmodul und ${\displaystyle \sigma _{6}=\sigma _{12},\,\varepsilon _{6}=2\varepsilon _{12}}$ zu beachten.

Allseitiger Druck

Hier sind die Normalspannungen gleich dem negativen Druck, ${\displaystyle \sigma _{1,2,3}=-p}$, Schubspannungen treten nicht auf, ${\displaystyle \sigma _{4,5,6}=0}$, und die Normaldehnungen sind alle gleich:

${\displaystyle \varepsilon _{1,2,3}={\frac {1}{E}}(1-\nu -\nu )\cdot (-p)\;\rightarrow \;-p={\frac {E}{1-2\nu }}\varepsilon _{1,2,3}}$

Die Volumendehnung ist ${\displaystyle \varepsilon _{v}=\varepsilon _{1}+\varepsilon _{2}+\varepsilon _{3}}$, sodass sich

${\displaystyle -p=K\,\varepsilon _{v},\quad K:={\frac {E}{3(1-2\nu )}}}$

ergibt, worin K der Kompressionsmodul ist.^[5]:97

Um physikalisch Sinn zu machen, muss das Material den Stabilitätskriterien genügen,

• dass es sich in Zugrichtung streckt, wenn man daran zieht, und nicht staucht,
• dass sich ein Zylinder bei Torsion im Sinn des angreifenden Drehmoments verwindet, und nicht dazu entgegengesetzt, und
• dass sich das Material unter Druck komprimiert und nicht expandiert.

Diese Kriterien entsprechen genauer der Forderung aus der Thermodynamik, dass die Formänderungsenergie bei Deformationen positiv ist. Die Formänderungsenergie berechnet sich in den quasi einachsigen #Materialversuchen, für die eine Spannungs-Dehnungs-Beziehung der Form σ=Cε charakteristisch ist, aus dem bestimmten Integral

${\displaystyle w(\varepsilon ):=\int _{0}^{\varepsilon }\sigma '\,{\rm {d}}\varepsilon '=\int _{0}^{\varepsilon }C\varepsilon '\,{\rm {d}}\varepsilon '=\left[C{\frac {{\varepsilon '}^{2}}{2}}\right]_{0}^{\varepsilon }={\frac {C}{2}}\varepsilon ^{2}}$

Damit dieser Wert für alle ε≠0 positiv ist, muss C positiv sein. Die Tabelle führt die Folgerungen hieraus im einzelnen auf.

Belastung	Ungleichung	Folgerung
Zug	${\displaystyle \varepsilon _{xx}\neq 0\;\rightarrow \;{\frac {E}{2}}\,\varepsilon _{xx}^{2}>0}$	${\displaystyle E>0}$
Torsion	${\displaystyle \varepsilon _{xy}\neq 0\;\rightarrow \;2G\,\varepsilon _{xy}^{2}>0}$	${\displaystyle G={\frac {E}{2(1+\nu )}}>0}$
Allseitiger Druck	${\displaystyle \varepsilon _{v}\neq 0\;\rightarrow \;{\frac {K}{2}}\varepsilon _{v}^{2}>0}$	${\displaystyle K={\frac {E}{3(1-2\nu )}}>0}$

Aus den letzten beiden Bedingungen resultieren Einschränkungen für die Poissonzahl:^[5]:98

${\displaystyle -1<\nu <{\frac {1}{2}}}$

Bei Inkompressibilität ist ν=½ und die Volumendehnung ist unabhängig vom Druck immer null. Der Druck ergibt sich dann nicht aus einer Materialgleichung (wie ${\displaystyle p=-K\,\varepsilon _{v}}$), sondern rein kinematisch aus der Nebenbedingung „Inkompressibilität“, siehe #Hookesches Gesetz für inkompressible Materialien.

Scheiben sind ebene Flächenträger, die per Definition nur in ihrer Ebene belastet werden. Stäbe und Balken sind schlanke Träger, bei denen zwei Abmessungen klein sind gegenüber der dritten axialen. Wenn keine Belastungen senkrecht zur Ebene bzw. Längsachse dieser Träger auftreten, herrscht in ihnen ein ebener Spannungszustand (ESZ), in dem alle Spannungskomponenten senkrecht zur betrachteten Ebene vernachlässigt werden können.

Flächenträger, die auch senkrecht zu ihrer Ebene belastet werden, bezeichnet man als Platten. Ist diese Platte so dick, dass sie durch die senkrecht auf sie wirkende Belastung nicht merklich zusammengedrückt wird, herrscht in ihrer Ebene ein ebener Verzerrungszustand (EVZ), in dem alle Verzerrungskomponenten senkrecht zur betrachteten Ebene vernachlässigt werden können.

Stäbe, Balken, Scheiben und Platten sind im Maschinenbau und Bauwesen weit verbreitete Konstruktionselemente. Daher lohnt es sich, die Elastizitätsbeziehung für den ESZ und EVZ aufzuschreiben.

Der ESZ entspricht in obiger Beziehung der Bedingung ${\displaystyle \sigma _{xz}=\sigma _{yz}=\sigma _{zz}=0}$. Dadurch vereinfacht sich die Elastizitätsbeziehung zu

${\displaystyle \left({\begin{array}{c}\varepsilon _{xx}\\\varepsilon _{yy}\\2\varepsilon _{xy}\end{array}}\right)={\frac {1}{E}}\left({\begin{array}{ccc}1&-\nu &0\\-\nu &1&0\\0&0&2(1+\nu )\end{array}}\right)\left({\begin{array}{c}\sigma _{xx}\\\sigma _{yy}\\\sigma _{xy}\end{array}}\right)}$

bzw.

${\displaystyle \left({\begin{array}{c}\sigma _{xx}\\\sigma _{yy}\\\sigma _{xy}\end{array}}\right)={\frac {E}{1-\nu ^{2}}}\left({\begin{array}{ccc}1&\nu &0\\\nu &1&0\\0&0&{\frac {1-\nu }{2}}\end{array}}\right)\left({\begin{array}{c}\varepsilon _{xx}\\\varepsilon _{yy}\\2\varepsilon _{xy}\end{array}}\right)}$

und ${\displaystyle \varepsilon _{zz}=-{\frac {\nu }{1-\nu }}(\varepsilon _{xx}+\varepsilon _{yy})=-{\frac {\nu }{E}}(\sigma _{xx}+\sigma _{yy})}$.

Im EVZ gilt ${\displaystyle \varepsilon _{xz}=\varepsilon _{yz}=\varepsilon _{zz}=0}$. Hieraus können dann folgende Zusammenhänge abgeleitet werden:

${\displaystyle \left({\begin{array}{c}\varepsilon _{xx}\\\varepsilon _{yy}\\\varepsilon _{xy}\end{array}}\right)={\frac {1}{2\mu }}\left({\begin{array}{ccc}1-\nu &-\nu &0\\-\nu &1-\nu &0\\0&0&1\end{array}}\right)\left({\begin{array}{c}\sigma _{xx}\\\sigma _{yy}\\\sigma _{xy}\end{array}}\right)}$.

bzw.

${\displaystyle \left({\begin{array}{c}\sigma _{xx}\\\sigma _{yy}\\\sigma _{xy}\end{array}}\right)={\frac {2\mu }{1-2\nu }}\left({\begin{array}{ccc}1-\nu &\nu &0\\\nu &1-\nu &0\\0&0&1-2\nu \end{array}}\right)\left({\begin{array}{c}\varepsilon _{xx}\\\varepsilon _{yy}\\\varepsilon _{xy}\end{array}}\right)}$

mit ${\displaystyle \sigma _{zz}=\nu (\sigma _{xx}+\sigma _{yy})=\lambda (\varepsilon _{xx}+\varepsilon _{yy})}$.

In Zylinderkoordinaten mit Abstand zur z-Achse ${\displaystyle r}$, Winkelkoordinate ${\displaystyle \theta }$, Höhenkoordinate ${\displaystyle z}$ und Lamé-Konstanten ${\displaystyle \mu ,\,\lambda }$ schreibt sich das Hookesche Gesetz:^[5]:102

${\displaystyle {\begin{aligned}\vartheta =&E_{rr}+E_{\theta \theta }+E_{zz}&=&{\frac {u_{r}}{r}}+{\frac {\partial u_{r}}{\partial r}}+{\frac {1}{r}}{\frac {\partial u_{\theta }}{\partial \theta }}+{\frac {\partial u_{z}}{\partial z}},\\\sigma _{rr}=&\lambda \vartheta +2\mu {\frac {\partial u_{r}}{\partial r}},&\sigma _{\theta \theta }=&\lambda \vartheta +2\mu {\frac {1}{r}}\left({\frac {\partial u_{\theta }}{\partial \theta }}+u_{r}\right),\\\sigma _{zz}=&\lambda \vartheta +2\mu {\frac {\partial u_{z}}{\partial z}},&\sigma _{r\theta }=&\mu \left[{\frac {1}{r}}\left({\frac {\partial u_{r}}{\partial \theta }}-u_{\theta }\right)+{\frac {\partial u_{\theta }}{\partial r}}\right],\\\sigma _{rz}=&\mu \left({\frac {\partial u_{r}}{\partial z}}+{\frac {\partial u_{z}}{\partial r}}\right),&\sigma _{z\theta }=&\mu \left({\frac {1}{r}}{\frac {\partial u_{z}}{\partial \theta }}+{\frac {\partial u_{\theta }}{\partial z}}\right)\end{aligned}}}$

In Kugelkoordinaten mit Abstand zum Ursprung ${\displaystyle \rho }$, Azimut ${\displaystyle \theta }$, Zenitwinkel ${\displaystyle \varphi }$ und Lamé-Konstanten ${\displaystyle \lambda ,\,\mu }$ schreibt sich das hookesche Gesetz mit den Winkelfunktionen Sinus sin und Kotangens cot:^[5]:102

${\displaystyle {\begin{aligned}\vartheta =&2{\frac {u_{\rho }}{\rho }}+{\frac {\partial u_{\rho }}{\partial \rho }}+{\frac {1}{\rho }}{\frac {\partial u_{\varphi }}{\partial \varphi }}+{\frac {1}{\rho \sin \varphi }}{\frac {\partial u_{\theta }}{\partial \theta }}+{\frac {u_{\varphi }}{\rho }}\cot \varphi ,\\\sigma _{\rho \rho }=&\lambda \vartheta +2\mu {\frac {\partial u_{\rho }}{\partial \rho }},\quad \sigma _{\varphi \varphi }=\lambda \vartheta +2\mu \left({\frac {1}{\rho }}{\frac {\partial u_{\varphi }}{\partial \varphi }}+{\frac {u_{\rho }}{\rho }}\right),\\\sigma _{\theta \theta }=&\lambda \vartheta +2\mu \left({\frac {1}{\rho \sin \varphi }}{\frac {\partial u_{\theta }}{\partial \theta }}+{\frac {u_{\rho }}{\rho }}+{\frac {u_{\varphi }}{\rho }}\cot \varphi \right)\\\sigma _{\rho \varphi }=&\mu \left[{\frac {1}{\rho }}\left({\frac {\partial u_{\rho }}{\partial \varphi }}-u_{\varphi }\right)+{\frac {\partial u_{\varphi }}{\partial \rho }}\right],\\\sigma _{\varphi \theta }=&\mu \left({\frac {1}{\rho \sin \varphi }}{\frac {\partial u_{\varphi }}{\partial \theta }}-{\frac {u_{\theta }}{\rho }}\cot \varphi +{\frac {1}{\rho }}{\frac {\partial u_{\theta }}{\partial \varphi }}\right),\\\sigma _{\theta \rho }=&\mu \left({\frac {\partial u_{\theta }}{\partial \rho }}+{\frac {1}{\rho \sin \varphi }}{\frac {\partial u_{\rho }}{\partial \theta }}-{\frac {u_{\theta }}{\rho }}\right)\end{aligned}}}$

Die Kontinuumsmechanik bevorzugt eine symbolische Schreibweise, die den Vorteil hat, kompakt und koordinaten­unabhängig zu sein. In der Materialtheorie werden Materialmodelle als Relation zwischen Spannungstensoren und Verzerrungstensoren formuliert, im linearen Bereich zwischen dem Cauchyschen Spannungstensor σ und dem linearisierten Verzerrungstensor ε.

In der linearen isotropen Elastizität kann der Spannungstensor nur von ε und seiner linearen Hauptinvariante Sp(ε) abhängen (Spur), weswegen nur zwei Material­parameter benötigt werden. Für das Modell der klassischen Theorie der linearen Elastizität existieren mehrere gleichbedeutende Formulierungen:^{[3]:185[11]:97f}

${\displaystyle {\begin{aligned}{\boldsymbol {\sigma }}=&2\mu \,{\boldsymbol {\varepsilon }}+\lambda \,{\rm {Sp}}({\boldsymbol {\varepsilon }})\,\mathbf {1} \\=&2G\,{\boldsymbol {\varepsilon }}^{\mathsf {D}}+K\,{\rm {Sp}}({\boldsymbol {\varepsilon }})\,\mathbf {1} \\=&{\frac {E}{1+\nu }}\left({\boldsymbol {\varepsilon }}+{\frac {\nu }{1-2\,\nu }}{\rm {Sp}}({\boldsymbol {\varepsilon }})\,\mathbf {1} \right)\end{aligned}}}$

Die umgekehrten Beziehungen lauten

${\displaystyle {\begin{aligned}{\boldsymbol {\varepsilon }}=&{\frac {1}{2\mu }}{\boldsymbol {\sigma }}-{\frac {\nu }{E}}{\rm {Sp}}({\boldsymbol {\sigma }})\,\mathbf {1} \\=&{\frac {1}{2G}}{\boldsymbol {\sigma }}^{\mathsf {D}}+{\frac {1}{9K}}{\rm {Sp}}({\boldsymbol {\sigma }})\,\mathbf {1} \\=&{\frac {1+\nu }{E}}\left({\boldsymbol {\sigma }}-{\frac {\nu }{1+\nu }}{\rm {Sp}}({\boldsymbol {\sigma }})\,\mathbf {1} \right)\end{aligned}}}$

Darin ist

Bezüglich der Standardbasis können obige Tensor­gleichungen als Matrizen­gleichungen dargestellt werden, beispiels­weise wird ${\displaystyle {\boldsymbol {\sigma }}=2\mu \,{\boldsymbol {\varepsilon }}+\lambda \,{\rm {Sp}}({\boldsymbol {\varepsilon }})\,\mathbf {1} }$ zu

${\displaystyle {\begin{pmatrix}\sigma _{11}&\sigma _{12}&\sigma _{13}\\\sigma _{12}&\sigma _{22}&\sigma _{23}\\\sigma _{13}&\sigma _{23}&\sigma _{33}\end{pmatrix}}=2\mu {\begin{pmatrix}\varepsilon _{11}&\varepsilon _{12}&\varepsilon _{13}\\\varepsilon _{12}&\varepsilon _{22}&\varepsilon _{23}\\\varepsilon _{13}&\varepsilon _{23}&\varepsilon _{33}\end{pmatrix}}+\lambda (\varepsilon _{11}+\varepsilon _{22}+\varepsilon _{33}){\begin{pmatrix}1&0&0\\0&1&0\\0&0&1\end{pmatrix}}}$.

Die Gleichung ist komponenten­weise zu verstehen, z. B. gilt ${\displaystyle \sigma _{11}=2\mu \varepsilon _{11}+\lambda (\varepsilon _{11}+\varepsilon _{22}+\varepsilon _{33}){\cdot }1}$. Diese Komponenten können allgemein mit der Einsteinschen Summen­konvention aufgeschrieben werden, derzufolge über doppelt vorkommende Indizes von eins bis drei zu summieren ist:

${\displaystyle \sigma _{ij}=2\mu \,\varepsilon _{ij}+\lambda \,(\varepsilon _{kk})\,\delta _{ij}}$

Der Einheitstensor wird hier durch das Kronecker-Delta δ repräsentiert. Diese drei Schreibweisen, symbolisch, als Matrizen oder mittels Komponenten sind als zueinander äquivalent anzusehen.

In inkompressiblen Materialien verschwindet die Volumendehnung ε_v überall und jederzeit. Die Volumendehnung ist gleich der ersten Hauptinvariante (Spur) des Verzerrungs­tensors, die bezüglich der Standardbasis

ε_v = Sp(ε) = ε₁₁ + ε₂₂ + ε₃₃

lautet, siehe den vorangegangenen Abschnitt #Hookesches Gesetz als Tensorgleichung, und die Dehnung ε_v ist hier null. Beim Zugversuch in 1-Richtung ist ε₂₂ = ε₃₃ = −ν·ε₁₁ und daher

ε_v = (1 − 2ν) ε₁₁ = 0

Bei Inkompressibilität ist ν = ½, E = 2(1 + ν) μ = 3μ, und der Kompressionsmodul ist nicht mehr definiert. Das Materialgesetz gilt nur noch für den gestalt­ändernden, volumen­erhaltenden, kurz deviatorischen Anteil:

σ^D = 2μ ε

Der komplementäre Kugelanteil des Spannungs­tensors ist der Drucktensor −p·1, der sich aus der Nebenbedingung Sp(ε) = 0. ergibt. Damit lautet die Spannungs-Dehnungs-Beziehung^[11]:101

σ = −p 1 + 2μ ε, Sp(ε) = 0

Im Zugversuch in 1-Richtung gibt es beispielsweise nur eine (vorgegebene) Normalspannung σ₁₁ in 1-Richtung und Schubspannungen treten nicht auf. Die Spur der Spannungs-Dehnungs-Beziehung liefert den Druck:

Sp(σ) = σ₁₁ = −p Sp(1) = −3p

Die 11-Komponente der Material­gleichung gibt die axiale Normaldehnung ε₁₁:

σ₁₁ = −p + 2μ ε₁₁ = ⅓ σ₁₁ + 2μ ε₁₁ → σ₁₁ = 3μ ε₁₁ = E ε₁₁

Die anderen Normal­dehnungen ergeben sich zu ε₂₂ = ε₃₃ = −½ ε₁₁.

Die Formänderungsenergie ist beim hookschen Material gegeben durch:^[3]:366

${\displaystyle w={\frac {1}{2}}\mathrm {Sp} ({\boldsymbol {\sigma }}{\boldsymbol {\varepsilon }})=\mu \,\mathrm {Sp} ({\boldsymbol {\varepsilon }}{\boldsymbol {\varepsilon }})+{\frac {\lambda }{2}}\mathrm {Sp} ({\boldsymbol {\varepsilon }})^{2}={\frac {1}{4\mu }}\mathrm {Sp} ({\boldsymbol {\sigma }}{\boldsymbol {\sigma }})-{\frac {\nu }{2E}}\mathrm {Sp} ({\boldsymbol {\sigma }})^{2}}$

Mit der Spur wird auch das Frobenius-Skalarprodukt „${\displaystyle :}$“ von Tensoren definiert:

${\displaystyle \mathbf {A} :\mathbf {B} :=\mathrm {Sp} (\mathbf {A} ^{\mathsf {T}}\cdot \mathbf {B} )}$

Damit schreibt sich die Formänderungsenergie

${\displaystyle w={\frac {1}{2}}{\boldsymbol {\sigma }}:{\boldsymbol {\varepsilon }}=\mu \,{\boldsymbol {\varepsilon }}:{\boldsymbol {\varepsilon }}+{\frac {\lambda }{2}}({\boldsymbol {\varepsilon }}:\mathbf {1} )^{2}={\frac {1}{4\mu }}{\boldsymbol {\sigma }}:{\boldsymbol {\sigma }}-{\frac {\nu }{2E}}({\boldsymbol {\sigma }}:\mathbf {1} )^{2}}$

Denn aus der Formänderungsenergie ergibt sich die Materialantwort aus der Ableitungsfunktion^[12]

${\displaystyle {\boldsymbol {\sigma }}={\frac {{\rm {d}}w({\boldsymbol {\varepsilon }})}{{\rm {d}}{\boldsymbol {\varepsilon }}}}}$   bzw.   ${\displaystyle {\boldsymbol {\varepsilon }}={\frac {{\rm {d}}w({\boldsymbol {\sigma }})}{{\rm {d}}{\boldsymbol {\sigma }}}}}$

Das hookesche Gesetz definiert demnach das lineare hyperelastische Material.

Der Elastizitätstensor ist die Ableitung^[12] der Spannungen nach den Verzerrungen und ist hier eine Konstante:

${\displaystyle \mathbb {C} ={\frac {{\rm {d}}{\boldsymbol {\sigma }}}{{\rm {d}}{\boldsymbol {\varepsilon }}}}=2\mu \,\mathbb {I} +\lambda \,\mathbf {1} \otimes \mathbf {1} }$

Darin ist ${\displaystyle \mathbb {I} }$ der Einheitstensor vierter Stufe und „⊗“ das dyadische Produkt.^[13] Aufgrund der Linearität ergibt sich das durch „Ausklammern“:

${\displaystyle {\begin{aligned}{\boldsymbol {\sigma }}&=2\mu \,{\boldsymbol {\varepsilon }}+\lambda \,{\rm {Sp}}({\boldsymbol {\varepsilon }})\,\mathbf {1} \\&=:2\mu \,\mathbb {I} :{\boldsymbol {\varepsilon }}+\lambda \,({\boldsymbol {\varepsilon }}:\mathbf {1} )\,\mathbf {1} \\&=:2\mu \,\mathbb {I} :{\boldsymbol {\varepsilon }}+\lambda \,(\mathbf {1} \otimes \mathbf {1} ):{\boldsymbol {\varepsilon }}\\&=(2\mu \,\mathbb {I} +\lambda \,\mathbf {1} \otimes \mathbf {1} ):{\boldsymbol {\varepsilon }}\\&=\mathbb {C} :{\boldsymbol {\varepsilon }}\end{aligned}}}$

Seine Inverse lautet

${\displaystyle \mathbb {S} :=\mathbb {C} ^{-1}={\frac {{\rm {d}}{\boldsymbol {\varepsilon }}}{{\rm {d}}{\boldsymbol {\sigma }}}}={\frac {1}{2\mu }}\,\mathbb {I} -{\frac {\nu }{E}}\,\mathbf {1} \otimes \mathbf {1} }$

Die Formänderungsenergie schreibt sich mit dem Elastizitätstensor:

w(ε) = ¹⁄₂ ε:ℂ:ε

oder

w(σ) = ¹⁄₂ σ:𝕊:σ

Der Elastizitätstensor hat zwei Eigenwerte:^[14]

1. Den Eigenwert 3K mit dem Einheitstensor als „Eigenvektor“:

${\displaystyle \mathbb {C} :\mathbf {1} =(2\mu \,\mathbb {I} +\lambda \,\mathbf {1} \otimes \mathbf {1} ):\mathbf {1} =(2\mu +\lambda \mathbf {1} :\mathbf {1} )\,\mathbf {1} =(2\mu +3\lambda )\,\mathbf {1} =3K\,\mathbf {1} }$

Der Drucktensor ist ein solcher Eigenvektor.

2. Den Eigenwert 2μ mit einem aus Deviatoren bestehenden Eigenraum, denn wegen ${\displaystyle {\rm {Sp}}(\mathbf {T} ^{D}):=\mathbf {1} :\mathbf {T} ^{D}:=0}$ ist

${\displaystyle \mathbb {C} :\mathbf {T} ^{D}=(2\mu \,\mathbb {I} +\lambda \,\mathbf {1} \otimes \mathbf {1} ):\mathbf {T} ^{D}=2\mu \,\mathbf {T} ^{D}+\lambda \,(\mathbf {1} :\mathbf {T} ^{D})\,\mathbf {1} =2\mu \,\mathbf {T} ^{D}}$

Der Verzerrungstensor ist bei volumentreuer Deformation (in erster Näherung) deviatorisch, was bei der reinen Scherung vorliegt.

Das Prinzip der materiellen Objektivität erfordert, dass ein Materialmodell der Elastizität in der lagrangeschen Betrachtungsweise formuliert wird, beispielsweise mit dem zweiten Piola-Kirchhoff’schen-Spannungstensor ${\displaystyle {\tilde {\mathbf {T} }}}$ und dem Green’schen Verzerrungstensor E:

${\displaystyle {\tilde {\mathbf {T} }}=2G\left({\mathbf {E} }+{\frac {\nu }{1-2\,\nu }}{\rm {Sp}}({\mathbf {E} })\mathbf {1} \right)}$

Jedes Modell der isotropen Hyperelastizität, das mit den beiden Tensoren ${\displaystyle {\tilde {\mathbf {T} }},{\mathbf {E} }}$ formuliert wird, geht bei physikalischer Linearisierung in dieses Gesetz über.^[3]:365 Bei geometrischer Linearisierung geht außerdem ${\displaystyle {\tilde {\mathbf {T} }}}$ in den Cauchyschen Spannungstensor σ und E in den linearisierten Verzerrungstensor ε über.

• Elastizitätstheorie
• Cauchy-Elastizität

Commons: Hookesches Gesetz – Sammlung von Bildern, Videos und Audiodateien

• Gesetz von Hooke bei LEIFIphysik (auf Schulniveau)

• Karl-Eugen Kurrer: Geschichte der Baustatik. Auf der Suche nach dem Gleichgewicht. Ernst und Sohn, Berlin 2016, ISBN 978-3-433-03134-6, S. 401 f. 
• Rolf D. Mahnken: Lehrbuch der Technischen Mechanik – Elastostatik. 1. Auflage. Springer Vieweg, Berlin 2015, ISBN 978-3-662-44797-0. 
• Sabina Muminovic: Die Kraft des Robert Hooke. Die wissenschaftshistorische Kontextualisierung des Hookeschen Gesetzes (= Peter Heering [Hrsg.]: Flensburg Studies on the History and Philosophy of Science and Science Education. Band 7). wbg Academic, Darmstadt 2022, ISBN 978-3-534-45026-8 (Open-Access-File [PDF; 28,7 MB]). 
• Ulrich Niewöhner-Desbordes: Enzyklopädie Medizingeschichte. Hrsg.: Werner E. Gerabek, Bernhard D. Haage, Gundolf Keil, Wolfgang Wegner. De Gruyter, Berlin, New York 2005, ISBN 3-11-015714-4, Hookesches Gesetz, S. 616. 
• Walter Schnell, Dietmar Gross, Werner Hauger: Technische Mechanik. Band 2: Elastostatik. Springer, Berlin 1998, ISBN 3-540-64147-5. 

1. ↑ ^{a b} Robert Hooke: A description of helioscopes and some other instruments made by Robert Hooke, Fellow of the Royal Society. Hrsg.: University of Michigan Library Digital Collections, Early English Books Online. 1676, S. 31 (umich.edu). 
2. ↑ ^{a b} Robert Hooke: De Potentia Restitutiva, or of Spring Explaining the Power of Springing Bodies. Hrsg.: University of Michigan Library Digital Collections, Early English Books Online. London 1678, S. 1 (umich.edu). 
3. ↑ ^{a b c d e f} P. Haupt: Continuum Mechanics and Theory of Materials. Springer, 2002, ISBN 978-3-642-07718-0, S. 379 ff., doi:10.1007/978-3-662-04775-0. 
4. ↑ ^{a b c d} István Szabó: Geschichte der mechanischen Prinzipien. Springer, 2013, ISBN 978-3-0348-5301-9 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 5. August 2025]). 
5. ↑ ^{a b c d e f g} T. M. Atanackovic, A. Guran: Theory of Elasticity for Scientists and Engineers. Springer Science+Business, 2000, ISBN 978-1-4612-7097-3, S. 102, doi:10.1007/978-1-4612-1330-7. 
6. ↑ ^{a b} H. Balke: Einführung in die Technische Mechanik. Festigkeitslehre. 3. Auflage. Springer-Vieweg, 2014, ISBN 978-3-642-40980-6, doi:10.1007/978-3-642-40981-3. 
7. ↑ D. Gross, W. Hauger, J. Schröder, W. A. Wall: Technische Mechanik. Elastostatik. Band 2. Springer-Verlag, Heidelberg 2014, ISBN 978-3-642-40965-3, S. 294, doi:10.1007/978-3-642-40966-0_6. 
8. ↑ Jürgen Dankert, Helga Dankert: Technische Mechanik. Statik, Festigkeitslehre, Kinematik/Kinetik. 5. Auflage. Vieweg+Teubner, 2009, ISBN 978-3-8351-0177-7, S. 535 (google.de). 
9. ↑ Eigenschaften Technischer Keramik. Verband der Keramischen Industrie e.V., abgerufen am 21. August 2025. 
10. ↑ J. M. Ball: Convexity conditions and existence theorems in non-linear elasticity. In: Archive for Rational Mechanics and Analysis. Band 63, 1977, S. 337–403. 
11. ↑ ^{a b} Ralf Greve: Kontinuumsmechanik. Ein Grundkurs für Ingenieure und Physiker. Springer, Berlin u. a. 2003, ISBN 978-3-642-62463-6, S. 97 ff., doi:10.1007/978-3-642-55485-8 (eingeschränkte Vorschau in der Google-Buchsuche). 
12. ↑ ^{a b} Die Fréchet-Ableitung einer Funktion f nach x ist der beschränkte lineare Operator ${\displaystyle {\mathcal {A}}}$ der – sofern er existiert – in allen Richtungen h dem Gâteaux-Differential entspricht, also

    ${\displaystyle {\mathsf {{\mathcal {A}}(h)=\left.{\frac {\mathrm {d} }{\mathrm {d} s}}f(x+s\,h)\right|_{s=0}=\lim _{s\rightarrow 0}{\frac {f(x+s\,h)-f(x)}{s}}}}}$

    für alle h gilt. Darin ist s∈ℝ, f, x und h skalar-, vektor- oder tensorwertig aber x und h gleichartig. Dann wird auch

    ${\displaystyle {\mathsf {{\mathcal {A}}={\frac {\mathrm {d} f}{\mathrm {d} x}}}}}$

    geschrieben.
13. ↑ Der Spannungs- und Verzerrungstensor sind Tensoren zweiter Stufe, für die die Addition untereinander, die Mulitplikation mit einem Skalar und das #Skalarprodukt „:“ definiert sind, siehe Tensorrechnung. Diese Tensoren sind damit Elemente eines euklidischen Vektorraums und können somit wie herkömmliche Vektoren (Tensoren erster Stufe) behandelt werden. Der Einheitstensor vierter Stufe 𝕀 ist definiert durch

    𝕀 :T = T  ∀ T

    Das dyadische Produkt „⊗“ wirkt hier wie bei den herkömmlichen Vektoren:

    (A⊗B):C = (B:C) A

    Insbesondere ist (1⊗1):A = (1:A) 1 = Sp(A) 1.
14. ↑ A. Bertram, J. Olschewski: Zur Formulierung anisotroper linearer anelastischer Stoffgleichungen mit Hilfe einer Projektionsmethode. In: Gesellschaft für Angewandte Mathematik und Mechanik (Hrsg.): Zeitschrift für Angewandte Mathematik und Mechanik. Band 73, Nr. 4–5, 1993, S. 401–403.