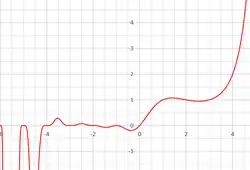
Barnessche
G
{\displaystyle G}
entlang der realen x-AchseDie Barnessche
G
{\displaystyle G}
, typischerweise mit
G
(
z
)
{\displaystyle G(z)}
Superfakultäten auf die komplexen Zahlen darstellt. Sie steht in Beziehung zur Gammafunktion , der
K
{\displaystyle K}
Konstanten von Glaisher-Kinkelin und ist nach dem Mathematiker Ernest William Barnes benannt.[ 1]
Formal ist die Barnessche
G
{\displaystyle G}
Weierstraß-Produkts definiert als
G
(
z
+
1
)
=
(
2
π
)
z
/
2
e
−
[
z
(
z
+
1
)
+
γ
z
2
]
/
2
∏
n
=
1
∞
[
(
1
+
z
n
)
n
e
−
z
+
z
2
/
(
2
n
)
]
{\displaystyle G(z+1)=(2\pi )^{z/2}e^{-[z(z+1)+\gamma z^{2}]/2}\prod _{n=1}^{\infty }\left[\left(1+{\frac {z}{n}}\right)^{n}e^{-z+z^{2}/(2n)}\right]}
wobei
γ
{\displaystyle \gamma }
Euler-Mascheroni-Konstante bezeichnet.
Differenzengleichung, Funktionalgleichung und spezielle Werte
Die Barnessche
G
{\displaystyle G}
Differenzengleichung
G
(
z
+
1
)
=
Γ
(
z
)
G
(
z
)
{\displaystyle G(z+1)=\Gamma (z)G(z)}
mit der Normierung
G
(
1
)
=
1.
{\displaystyle G(1)=1.}
G
{\displaystyle G}
ganzzahlige Argumente annimmt:
G
(
n
)
=
{
0
,
falls
n
=
0
,
−
1
,
−
2
,
…
∏
i
=
0
n
−
2
i
!
,
falls
n
=
1
,
2
,
…
{\displaystyle G(n)={\begin{cases}0,&{\text{falls }}n=0,-1,-2,\ldots \\\prod _{i=0}^{n-2}i!,&{\text{falls }}n=1,2,\ldots \end{cases}}}
so dass
G
(
n
)
=
(
Γ
(
n
)
)
n
−
1
K
(
n
)
{\displaystyle G(n)={\frac {(\Gamma (n))^{n-1}}{K(n)}}}
wobei
Γ
(
n
)
{\displaystyle \Gamma (n)}
K
(
n
)
{\displaystyle K(n)}
K-Funktion bezeichnen. Die Differenzengleichung definiert die
G
{\displaystyle G}
Konvexitätsbedingung
(
∀
x
≥
1
)
d
3
d
x
3
log
(
G
(
x
)
)
≥
0
{\displaystyle (\forall x\geq 1)\,{\frac {\mathrm {d} ^{3}}{\mathrm {d} x^{3}}}\log(G(x))\geq 0}
gestellt wird.[ 2]
Die Differenzengleichung der
G
{\displaystyle G}
Funktionalgleichung der Gamma-Funktion liefern die folgende Funktionalgleichung für die
G
{\displaystyle G}
Hermann Kinkelin bewiesen wurde:
G
(
1
−
z
)
=
G
(
1
+
z
)
1
(
2
π
)
z
exp
∫
0
z
π
t
cot
π
t
d
t
.
{\displaystyle G(1-z)=G(1+z){\frac {1}{(2\pi )^{z}}}\exp \int \limits _{0}^{z}\pi t\cot \pi t\,\mathrm {d} t.}
Wie die Gamma-Funktion erfüllt auch die
G
{\displaystyle G}
[ 3]
G
(
n
z
)
=
K
(
n
)
n
n
2
z
2
/
2
−
n
z
(
2
π
)
−
n
2
−
n
2
z
∏
i
=
0
n
−
1
∏
j
=
0
n
−
1
G
(
z
+
i
+
j
n
)
{\displaystyle G(nz)=K(n)n^{n^{2}z^{2}/2-nz}(2\pi )^{-{\frac {n^{2}-n}{2}}z}\prod _{i=0}^{n-1}\prod _{j=0}^{n-1}G\left(z+{\frac {i+j}{n}}\right)}
wobei
K
(
n
)
{\displaystyle K(n)}
K
(
n
)
=
e
−
(
n
2
−
1
)
ζ
′
(
−
1
)
⋅
n
5
12
⋅
(
2
π
)
(
n
−
1
)
/
2
=
(
A
e
−
1
12
)
n
2
−
1
⋅
n
5
12
⋅
(
2
π
)
(
n
−
1
)
/
2
.
{\displaystyle K(n)=e^{-(n^{2}-1)\zeta ^{\prime }(-1)}\cdot n^{\frac {5}{12}}\cdot (2\pi )^{(n-1)/2}\,=\,(Ae^{-{\frac {1}{12}}})^{n^{2}-1}\cdot n^{\frac {5}{12}}\cdot (2\pi )^{(n-1)/2}.}
gegeben ist. Hierbei ist
ζ
′
{\displaystyle \zeta ^{\prime }}
Riemannschen Zeta-Funktion und
A
{\displaystyle A}
Konstante von Glaisher-Kinkelin .
Asymptotische Entwicklung
Die Funktion
log
G
(
z
+
1
)
{\displaystyle \log \,G(z+1)}
log
G
(
z
+
1
)
=
1
12
−
log
A
+
z
2
log
2
π
+
(
z
2
2
−
1
12
)
log
z
−
3
z
2
4
+
∑
k
=
1
N
B
2
k
+
2
4
k
(
k
+
1
)
z
2
k
+
O
(
1
z
2
N
+
2
)
.
{\displaystyle \log G(z+1)={\frac {1}{12}}-\log A+{\frac {z}{2}}\log 2\pi +\left({\frac {z^{2}}{2}}-{\frac {1}{12}}\right)\log z-{\frac {3z^{2}}{4}}+\sum _{k=1}^{N}{\frac {B_{2k+2}}{4k\left(k+1\right)z^{2k}}}+O\left({\frac {1}{z^{2N+2}}}\right).}
Hierbei bezeichnet
B
k
{\displaystyle B_{k}}
Bernoulli-Zahlen und
A
{\displaystyle A}
Konstante von Glaisher-Kinkelin . (Man beachte, dass zur Zeit von Barnes[ 4]
B
2
k
{\displaystyle B_{2k}}
(
−
1
)
k
+
1
B
k
{\displaystyle (-1)^{k+1}B_{k}}
z
{\displaystyle z}
Weblink
Einzelnachweise
↑ Ernest W. Barnes: The theory of the
G
{\displaystyle G}
The Quarterly Journal of Pure and Applied Mathematics , Bd. 31 (1900), Seiten 264–314.
↑ Marie-France Vignéras : L'équation fonctionelle de la fonction zêta de Selberg du groupe modulaire
S
L
(
2
,
Z
)
{\displaystyle SL(2,\mathbb {Z} )}
. In: Astérisque , Bd. 61 (1979), Seiten 235–249, ISSN 0303-1179 ↑ Moshe Y. Vardi : Determinants of Laplacians and multiple gamma functions. In: SIAM Journal on Mathematical Analysis , Bd. 19 (1988), Seiten 493–507, ISSN 0036-1410 ↑ Edmund Taylor Whittaker , George N. Watson: A Course of Modern Analysis. 4. Aufl. Cambridge University Press, Cambridge 1990, ISBN 978-0-521-09189-3.