Zwillingsparadoxon

Das Zwillings- oder Uhrenparadoxon ist die paradox erscheinende Tatsache, dass Zwillinge verschiedenes Alter erreicht haben, wenn einer von ihnen eine Rundreise macht und der andere zu Hause bleibt: Beim Wiedersehen ist der daheimgebliebene Zwilling älter als der zurückgekehrte. Das Zwillingsparadoxon wurde als Gedankenexperiment erstmals 1905 von Albert Einstein aus seiner damals neuen Relativitätstheorie abgeleitet. Der Effekt ist rein physikalischer Natur. Entsprechend geht auch eine Uhr auf einer Rundreise nach, wenn man sie bei der Rückkehr mit einer am Ort verbliebenen Uhr vergleicht. Der Effekt ist unmerklich klein bei Reisen mit alltagsüblichen Geschwindigkeiten, konnte jedoch erstmals 1971 im Hafele-Keating-Experiment mithilfe von Atomuhren bei einer Weltreise per Linienflugzeug nachgewiesen werden.

Das Zwillingsparadoxon macht deutlich, dass die Zeit keine gegebene physikalische Größe ist, die im ganzen Universum den gleichen Wert hat, und dass es von den näheren Umständen abhängt, wie schnell sie jeweils fortschreitet. Beides widerspricht der Alltagserfahrung sowie der grundlegenden Annahme einer absoluten Zeit in der klassischen Physik seit Isaac Newton, wurde aber seither in zahllosen physikalischen Experimenten bestätigt.^[1][2][3]

Des Weiteren scheint nach oberflächlicher Anwendung des Relativitätsprinzips zunächst ausgeschlossen, dass überhaupt ein Unterschied im Alter der Zwillinge bzw. dem Stand der Uhren entstehen soll. Dem Relativitätsprinzip zufolge sind alle physikalischen Bezugssysteme darin gleichwertig, die Folgen eines Experiments vorherzusagen. Vom Bezugssystem des reisenden Zwillings aus gesehen ist es aber der andere, der sich wie auf einer Rundreise erst entfernt und dann zurückkehrt, so dass dieser nun der jüngere sein sollte. Diese entgegengesetzten Erwartungen an das erreichte Alter sind logisch unvereinbar, denn beim Wiedersehen kann — wenn überhaupt — nur einer der jüngere sein. Der Fehler beruht darauf, dass hier das Relativitätsprinzip falsch vereinfacht wurde. Bei sorgfältiger Anwendung der Regeln, mit deren Hilfe man die Beobachtungen des einen Zwillings in das Bezugssystem des anderen umzurechnen hat, ergibt sich für beide Zwillinge übereinstimmend, dass der daheimgebliebene beim Wiedersehen der ältere ist.

Diese Regeln sind in der Lorentztransformation zusammengefasst, die ihrerseits eine direkte Folge des Relativitätsprinzips in Verbindung mit dem Prinzip der Konstanz der Lichtgeschwindigkeit ist. Aus der Lorentztransformation ergibt sich u. a., dass räumliche Abstände für einen Beobachter in einem bewegten Bezugssystem umso stärker verkürzt sind, je schneller sich das Bezugssystem bewegt (Lorentz-Kontraktion). Daher ist für den reisenden Zwilling die zurückgelegte Strecke kürzer, als der daheimgebliebene sie in seinem Bezugssystem beobachtet. Da die Reisegeschwindigkeit in beiden Bezugssystemen aber denselben Wert hat, ist die Reise für den reisenden Zwilling auch schneller beendet als für den daheimgebliebenen. Folglich ist der reisende Zwilling bei seiner Rückkehr weniger gealtert.

Im Einzelnen lassen sich diese Zusammenhänge an einem einfachen Beispiel gut verfolgen: Betty fliegt mit 80 % der Lichtgeschwindigkeit zu einem Stern. Ihre Zwillingsschwester Anna bleibt auf der Erde, die hier vereinfacht als ruhendes Inertialsystem angesehen werden soll. Anna weiß, dass der Stern sich in einer gleichbleibenden Entfernung von acht Lichtjahren zur Erde befindet, so dass Betty für den Hinflug zehn Jahre braucht. Betty kehrt sogleich wieder zurück, so dass Anna sie nach weiteren 10 Jahren wieder auf der Erde begrüßen kann. Anna ist 20 Jahre älter geworden, so zeigt es auch ihre Kalenderuhr an. Betty meint aber, ihre Reise habe nur 12 Jahre gedauert, und belegt dies mit ihrer genau gleichartigen Uhr, die sie mitgenommen hatte.^[2]

Beide haben recht. Widersprüchlich oder paradox erscheint dies aber, wenn man – der Alltagserfahrung folgend – davon ausgeht, dass Zeit eine unbeeinflussbare physikalische Größe ist, die im ganzen Universum gleichmäßig fortschreitet. Diese Annahme ist jedoch unzutreffend, wie zuerst von Albert Einstein gezeigt worden ist. Nach der von ihm ausgearbeiteten Relativitätstheorie, die heute in zahllosen Beobachtungen bestätigt ist, gibt es keine universelle Zeit. Vielmehr muss für jedes Bezugssystem eine eigene Zeit angesetzt werden. Die Uhren von Anna und Betty gehen nur dann gleich schnell, wenn sie relativ zueinander in Ruhe sind. Solange aber Betty sich mit einer Geschwindigkeit ${\displaystyle v\neq 0}$ entfernt oder nähert, läuft ihre Uhr im Vergleich zur Zeit von Annas Ruhesystem um den Faktor

${\displaystyle \gamma ^{-1}={\sqrt {1-\left({\frac {v}{c}}\right)^{2}}}}$

langsamer (siehe relativistische Zeitdilatation, ${\displaystyle c}$ ist die Lichtgeschwindigkeit). Dieser Faktor ist der Kehrwert des in der Relativitätstheorie häufig anzuwendenden Lorentzfaktors ${\displaystyle \gamma }$. Für kleine Geschwindigkeiten (${\displaystyle v\ll c}$) ist der Faktor praktisch gleich 1, die resultierende Auswirkung also nicht spürbar, er kann bei Annäherung an die Lichtgeschwindigkeit aber sehr klein werden.

Für das Beispiel wurde eine bei Raketenreisen technisch unrealistisch große Geschwindigkeit gewählt, um die Folgen zu verdeutlichen. Bettys Zeit geht demnach um den Faktor

${\displaystyle \gamma ^{-1}={\sqrt {1-0{,}8^{2}}}={\sqrt {0{,}36}}=0{,}6}$

langsamer als die Zeit von Anna. Sowohl für den Hinflug als auch für den Rückflug braucht Betty in ihrer eigenen Zeit nicht 10 Jahre, sondern nur ${\displaystyle 0{,}6\cdot 10=6}$ Jahre. So ergibt sich, dass bei der Rückkehr die Uhr in Bettys Rakete nur 12 Jahre vorangeschritten ist, während ihre Abwesenheit in der Erdzeit ausgedrückt für Anna 20 Jahre dauerte. Sämtliche Vorgänge aller Arten, die zwischen Abflug und Rückkehr passieren, haben für Anna insgesamt 20 Jahre gedauert, für Betty nur 12. So ist zum Beispiel auch Anna 20 Jahre älter geworden, Betty nur 12. Sobald aber Anna und Betty wieder ein gemeinsames Ruhesystem haben und gleichzeitig ihre Uhren ablesen können, vergeht die Zeit für beide wieder gleich schnell.

Aus dem entstandenen Altersunterschied ergibt sich ein zweiter Aspekt des Paradoxons: Sollte nun nicht auch Anna jünger sein als Betty? Von Betty aus gesehen ist es doch die auf der Erde bleibende Schwester Anna, die sich von ihr erst entfernt und dann zu ihr zurückkommt. Dann sollte es aufgrund derselben Überlegungen wie oben doch umgekehrt Anna sein, die nun jünger ist als Betty. Aber dass jede von beiden die Jüngere sein soll, ist logisch unmöglich. Für die Auflösung dieses Paradoxons ist zu beachten, dass der Lorentzfaktor für die Berechnung benötigt wird, mit der man die Raum-Zeit-Koordinaten desselben Ereignisses von einem Bezugssystem ins andere übersetzt, während wirkliche Paradoxien nur entstehen, wenn gemachte Beobachtungen einander widersprechen.

Um das näher auszuführen, nehmen wir an, dass Anna und Betty mithilfe von Teleskopen gegenseitig ihre Uhren beobachten können. Wenn Betty im Jahr 2000 gestartet ist, kommt sie nach Annas Zeitskala 2010 am Stern an. Wenn sich auf dem Stern, der relativ zur Erde ja in Ruhe ist, eine dritte Uhr befände, würde sie die Zeit von Annas Bezugssystem anzeigen, also das Jahr 2010. Bettys Uhr zeigt am selben Ort dann aber das Jahr 2006. Der Unterschied zur auf dem Stern ruhenden Uhr ist die mit dem Lorentzfaktor berechnete relativistische Zeitdilatation. Sehen kann Anna die Ankunft von Betty am Stern wegen der Laufzeit des Lichts aber erst 8 Jahre später, für sie also im Jahr 2018. Eine schnellere Übertragung des Bildes zu Erde ist physikalisch unmöglich. Demnach beobachtet Anna den Hinflug ihrer Schwester 18 Jahre lang, dreimal länger als die 6 Jahre, die Anna dafür auf Bettys Uhr abliest. Der Unterschied zur reinen Zeitdilatation entsteht durch den Doppler-Effekt. Nach der Klassischen Physik erzeugt er, wenn der Abstand zunimmt, in den Beobachtungen eine Zeitdehnung um den Faktor ${\displaystyle (1-v/c)}$, und für die relativistische Berechnung muss noch die Zeitdilatation mit dem oben genannten Lorentzfaktor ${\displaystyle 1/{\sqrt {1-({\tfrac {v}{c}})^{2}}}}$ berücksichtigt werden. Das Produkt aus beiden Faktoren ist ${\displaystyle {\sqrt {\tfrac {c-v}{c+v}}}}$ und hat hier den Wert 1/3. Das heißt: Wenn Anna einen Vorgang in Bettys Rakete beobachtet, dann läuft er in ihrer Wahrnehmung dreimal langsamer ab, als Betty es in ihrem Ruhesystem beobachtet. Das gilt auch umgekehrt: Wenn Betty in ihrem Jahr 2006 am Stern ankommt, ist es bei Anna das Jahr 2010, aber das Bild von Annas Uhr, das Betty bei ihrer Landung am Stern empfängt, war schon 8 Jahre früher gesendet worden. Daher sieht Betty Annas Uhr, wie diese das Jahr 2002 anzeigt. Auch Betty beobachtet also, dass Annas Uhr dreimal langsamer geht als ihre eigene. Wenn Betty danach zurüçkfliegt, was nach ihrer Zeit 6 Jahre dauert, kehrt sich der Dopplerfaktor um (weil in der Formel das Vorzeichen von ${\displaystyle v}$ wechselt): Jetzt sieht Betty Annas Uhr und alle anderen Vorgänge bei Anna nicht dreimal langsamer laufen als ihre eigene, sondern dreimal schneller. Zum Beispiel sieht Betty während des Rückflugs die Erde nicht sechsmal um die Sonne kreisen, sondern 18 mal. Wenn Betty dann auf der Erde landet, weiß sie, dass dort das Jahr 2020 ist, dass also Anna 20 Jahre älter geworden ist, sie selbst aber nur 12. Es gibt keinen Widerspruch zwischen den Beobachtungen von Anna und Betty.

Albert Einstein wies im Jahre 1905 darauf hin, dass eine Uhr, die sich von einem beliebigen Punkt entfernt und dorthin zurückkehrt, gegenüber einer am Ausgangspunkt zurückgelassenen unbewegten Uhr nachgeht.^[4] 1911 dehnte er diese Überlegung auf lebende Organismen aus:

Noch im selben Jahr formulierte auch Paul Langevin das Paradoxon:

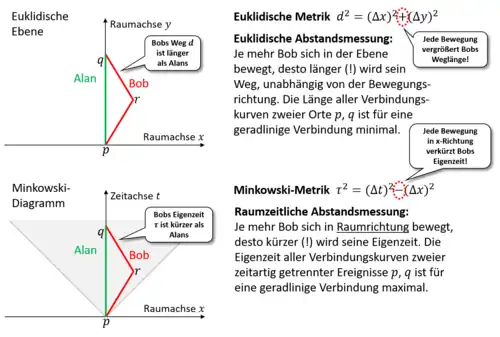
In Newtons Vorstellung gibt es einen absoluten Raum mit der uns vertrauten euklidischen Abstandsmessung und einer absoluten Zeit, Raum und Zeit sind nicht miteinander verwoben. Die absolute Zeit verstreicht in Newtons Vorstellung für jeden Beobachter gleich, unabhängig von seinem Ort und seinem Bewegungszustand. Einstein hat das Newtonsche Paradigma jedoch mit seiner Relativitätstheorie verworfen, jeder Beobachter hat seine eigene „persönliche“ Zeit, die sog. Eigenzeit, die dadurch zustande kommt, dass Raum und Zeit über die Minkowski-Metrik untrennbar miteinander zu einer Einheit verknüpft sind, der sog. Raumzeit.

Hierbei ist eine Metrik eine Vorschrift, die festlegt, wie Abstände im zugrundeliegenden Raum gemessen werden. Die euklidische Metrik ${\displaystyle d^{2}=(\Delta x)^{2}+(\Delta y)^{2}}$ etwa bestimmt, wie räumliche Abstände ${\displaystyle d}$ in der Ebene zu messen sind; diese pythagoreische Addition lernt man schon in der Schule. Die Minkowski-Metrik ${\displaystyle \tau ^{2}}$ in der 4-dimensionalen Raumzeit bestimmt, wie Raumzeitabstände ${\displaystyle \tau }$ zu messen sind. In der Minkowski-Metrik stellt die Naturkonstante ${\displaystyle c}$, die Lichtgeschwindigkeit, den Umrechnungsfaktor dar, der die Zeitachse formal in eine Raumachse konvertiert. Im einfachsten Fall von zwei Dimensionen (man bewegt sich räumlich nur in einer Dimension) ist die Minkowski-Metrik ${\displaystyle \tau ^{2}}$ gegeben durch eine der pythagoreischen Addition ähnliche Vorschrift (jedoch mit einem Minuszeichen):

${\displaystyle (c\tau )^{2}=(c\Delta t)^{2}-(\Delta x)^{2}}$ bzw. (wenn man ${\displaystyle c=1}$ setzt) durch ${\displaystyle \tau ^{2}=(\Delta t)^{2}-(\Delta x)^{2}}$.

Graphisch kann man die Raumzeit im 2-dimensionalen Fall durch ein Minkowski-Diagramm darstellen (vgl. Abb. 1, unteres Bild); dies ist letztlich ein gewöhnliches Weg-Zeit-Diagramm, in dem die Zeitachse mit dem Umrechnungsfaktor multipliziert und für raumzeitliche Abstandsmessungen die Minkowski-Metrik verwendet wird. Raumzeitpunkte im Minkowski-Diagramm nennt man Ereignisse und Kurven Weltlinien. Die „Länge“ ${\displaystyle \tau }$ einer zeitartigen Weltlinie heißt Eigenzeit und gibt die Zeitspanne an, die für einen Beobachter, dessen Bewegung in der Raumzeit durch diese Weltlinie beschrieben wird, gemäß einer von ihm mitgeführten Uhr zwischen Anfangs- und Endpunkt der Weltlinie gemessen wird (vgl. Abb. 2). Zeitartig bedeutet hierbei vereinfacht ausgedrückt, dass der Beobachter sich stets mit Unterlichtgeschwindigkeit bewegt. Die Winkelhalbierenden (und Geraden parallel dazu) sind Weltlinien von Photonen (Licht).

Hervorzuheben ist, dass nicht das Diagramm selbst die Besonderheit darstellt, sondern die Art der raumzeitlichen Abstandsmessung. Folgendes gilt:

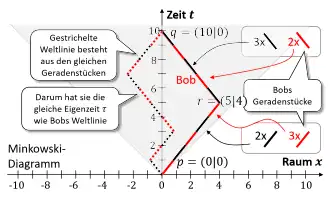
1. Eigenzeiten ${\displaystyle \tau }$ für zeitartige Weltlinien, die sich aus Geradenstücken zusammensetzen, werden mit obiger Formel für jedes Geradenstück einzeln berechnet und dann aufsummiert.

2. Zwei zeitartige Weltlinien mit gleichem Anfangs- und Endpunkt haben identische Eigenzeiten, wenn ihre Zusammensetzung aus Geradenstücken übereinstimmt (vgl. Abb. 2).

Analoge Eigenschaften gelten ebenso für die Länge von Kurven in der euklidischen Ebene. Der Vorzeichenwechsel zwischen zeitlichen und räumlichen Komponenten in der Minkowski-Metrik (siehe obige Formel) allerdings – dieser kleine Unterschied gegenüber der euklidischen Abstandsmessung (vgl. Abb. 1) – impliziert folgende aufgrund unser euklidischen Denkgewohnheiten kontraintuitive Eigenschaft der Minkowski-Geometrie (also der speziellen Relativitätstheorie):

3. Von zwei zeitartigen Weltlinien mit gleichem Anfangs- und Endpunkt im Minkowski-Diagramm, hat die optisch länger wirkende („euklidische Wahrnehmung“) einen kleineren Raumzeitabstand bzgl. der Minkowski-Metrik, d. h. eine kürzere Eigenzeit (vgl. Abb. 1).

Die Minkowski-Metrik ist Stand heute die angemessene geometrische Beschreibung für unser Universum, wenn man es als global flach annimmt (bei Beschränkung auf kurze Zeitspannen und räumlich kleine Umgebungen stellt die Minkowski-Metrik oft eine hinreichend gute Näherung dar; man sagt dazu: das Universum ist lokal flach und kann lokal näherungsweise durch die Minkowski-Geometrie beschrieben werden).

Der Vorzeichenwechsel in der Minkowski-Metrik ist somit Ursache dafür, dass die Weltlinie des gereisten Zwillings bzgl. der Minkowski-Metrik (d. h. seine Eigenzeit) kürzer ist als die des daheimgebliebenen und der gereiste Zwilling somit weniger altert als der daheimgebliebene.

Beispiel zur Berechnung von Eigenzeiten und Gangunterschied der Uhren

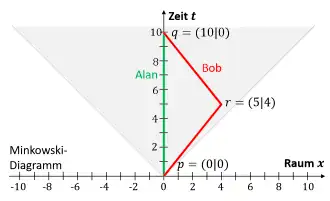
Im Folgenden werden die Eigenzeiten ${\displaystyle \tau }$ für die Weltlinien vom auf der Erde verbleibenden Alan und dem gereisten Bob beispielhaft gemäß Abb. 3 berechnet; hierbei reise Bob mit 80 % Lichtgeschwindigkeit an einen 4 Lichtjahre entfernten Ort und kehre dann augenblicklich mit gleicher Geschwindigkeit zurück. Die Raumzeitpunkte ${\displaystyle (t|x)}$ seien also ${\displaystyle p=(0|0),r=(5|4),q=(10|0)}$.

Alans Weltlinie setzt sich aus nur einem Geradenstück ${\displaystyle {\overline {pq}}}$ zusammen. Für die Ereignisse ${\displaystyle p=(0|0)}$ und ${\displaystyle q=(10|0)}$ beträgt die Zeitdifferenz ${\displaystyle \Delta t=10-0=10}$ und die räumliche Differenz ${\displaystyle \Delta x=0-0=0}$. Mit obiger Formel und c=1 erhält man

${\displaystyle \tau ({\overrightarrow {pq}})={\sqrt {(\Delta t)^{2}-(\Delta x)^{2}}}={\sqrt {10^{2}-0^{2}}}=10}$

Alans Eigenzeit ${\displaystyle \tau ({\text{Alan}})=10}$ stimmt mit der Koordinatenzeit (= was man an der Zeitachse abliest) im Minkowski-Diagramm von Abb. 3 überein. Das liegt daran, dass dieses Koordinatensystem mit Alans Inertialsystem übereinstimmt.

Gemäß Newtons absolutem Zeitbegriff dürfte man die für Bob während seiner Reise verstrichene Zeit ebenfalls an dieser Zeitachse ablesen; gemäß Einsteins Relativitätstheorie ist jedoch stattdessen Bobs Eigenzeit zu verwenden. Diese lässt sich für ein Geradenstück dennoch recht einfach mit an diesem Koordinatensystem ablesbaren Daten berechnen, nämlich indem man Zeit- und Ortsdifferenz ${\displaystyle \Delta t}$ bzw. ${\displaystyle \Delta x}$ aus Anfangs- und Endpunkt des Geradenstücks bildet und in die obige Formel für ${\displaystyle \tau }$ einsetzt.

Bobs Weltlinie setzt sich aus zwei Geradenstücken zusammen, welche durch die Raumzeitpunkte ${\displaystyle p,r}$ und ${\displaystyle q}$ festgelegt sind. Für das Geradenstück ${\displaystyle {\overline {rq}}}$ erhält man aus den Raumzeitpunkten ${\displaystyle (t|x)}$ durch Differenzbildung: ${\displaystyle {\overrightarrow {rq}}=q-r=(\Delta t|\Delta x)=(10-5|0-4)=(5|-4)}$. Bobs Eigenzeit für das Geradenstück ${\displaystyle {\overline {rq}}}$ lautet daher

${\displaystyle \tau ({\overrightarrow {rq}})={\sqrt {(\Delta t)^{2}-(\Delta x)^{2}}}={\sqrt {5^{2}-(-4)^{2}}}=3}$.

Bobs Eigenzeit für das Geradenstück ${\displaystyle {\overline {pr}}}$ ist identisch. Da sich die Eigenzeit einer aus Geradenstücken zusammengesetzten Weltlinie durch Aufsummieren ergibt, erhält man für Bobs Eigenzeit ${\displaystyle \tau ({\text{Bob}})=3+3=6}$. Somit gilt

${\displaystyle \tau ({\text{Alan}})=\tau ({\overrightarrow {pq}})=10>\underbrace {\tau ({\overrightarrow {pr}})} _{=3}+\underbrace {\tau ({\overrightarrow {rq}})} _{=3}=6=\tau ({\text{Bob}})}$

Mit einem Altersunterschied von 4 Jahren ist Bob langsamer gealtert als sein daheim gebliebener Zwilling Alan. Man sieht: Bei Alan wird nichts abgezogen, weil er sich in der Raumzeit nicht in x-Richtung, sondern nur in t-Richtung „bewegt“. Bob hat Bewegungsanteile in x-Richtung und macht „Umwege“, darum verringert sich seine Eigenzeit.

Die hier stehende Ungleichung ist ein konkretes Beispiel für die in Minkowski-Räumen geltende inverse Dreiecksungleichung. Diese ist zunächst ein rein mathematischer Lehrsatz. Im physikalischen Zusammenhang liefert sie den Grund für den Gangunterschied der Uhren. Eine Ganggleichheit kann nur eintreten, wenn die Ereignisse p, r und q auf einer Geraden liegen.

In Lehre und Literatur wird teils behauptet, dass die mehrfachen Beschleunigungen bzw. Bezugssystemwechsel Grund für das langsamere Altern des gereisten Zwillings seien. Das ist jedoch nicht richtig. Die Inkorrektheit dieser Behauptung kann man mithilfe des Gegenbeispiels aus Abb. 4 einsehen, in welchem das Gedankenexperiment aus Abb. 3 folgendermaßen abgewandelt wird:

Statt des geradlinigen Weges in der Raumzeit werden für Alan „Umwege“ in Form der gleichen Beschleunigungsphasen wie für Bob angenommen (nur zu anderen Zeitpunkten); alle übrigen Daten werden aus vorangehendem Beispiel übernommen. Die Beschleunigungsphasen für Alan seien gemäß Abb. 4 durch die Ereignisse ${\displaystyle a_{1}=(4|0),a_{2}=(5|0{,}8),a_{3}=(6|0)}$ gegeben. Das heißt: 4 Jahre nach Abflug von Bob bricht auch Alan auf und entfernt sich mit 80 % Lichtgeschwindigkeit um 0,8 Lichtjahre von der Erde, kehrt dann mit gleicher Geschwindigkeit zurück und wartet anschließend auf Bob, der dieselbe Reise wie vorher unternimmt. Damit berechnet man für Alans Weltlinie „mit Umwegen“

${\displaystyle \tau ({\overrightarrow {pa_{1}}})=\tau ({\overrightarrow {a_{3}q}})=4}$, ${\displaystyle \tau ({\overrightarrow {a_{1}a_{2}}})=\tau ({\overrightarrow {a_{2}a_{3}}})={\sqrt {1^{2}-0{,}8^{2}}}=0{,}6}$ ${\displaystyle \Rightarrow \tau ({\text{Alan mit Umwegen}})=4+0{,}6+0{,}6+4=9{,}2}$

Ein Vergleich zeigt ${\displaystyle \tau ({\text{Alan mit Umwegen}})=9{,}2>6=\tau ({\text{Bob}})}$, d. h. Bob ist mit einem Altersunterschied von 3,2 Jahren langsamer gealtert als Alan – und zwar trotz identischer Beschleunigungsphasen bzw. Bezugssystemwechsel. Dies widerlegt obige Behauptung.

Solange die „Umwege“ in Alans Weltlinie nicht zu groß werden, bleibt Bobs Eigenzeit kürzer als Alans. Die eigentliche Ursache für Bobs langsameres Altern ist also, dass er „größere Umwege“ in der Raumzeit als Alan nimmt, um vom Raumzeitpunkt p zum Raumzeitpunkt q zu gelangen. Beschleunigungen spielen zwar insofern auch eine sekundäre Rolle, als dass „Umwege“ natürlich nur möglich sind, wenn längs der Weltlinie Beschleunigungen stattfinden (bzw. insofern als dass ohne sie keine Rückkehr möglich wäre); aber sie sind nicht der eigentliche Grund, denn Alan und Bob haben in dem konstruierten Gedankenexperiment (Abb. 4) genau die gleichen Beschleunigungsphasen.

• Garagenparadoxon
• Bellsches Raumschiffparadoxon

• Roman Sexl, Herbert Kurt Schmidt: Raum – Zeit – Relativität. Relativistische Phänomene in Theorie und Beispiel, Kap 5.2–5.4. Vieweg, Braunschweig und Wiesbaden 2001, ISBN 3-528-37236-2.
• Sean M. Carroll: The Biggest Ideas in the Universe: Space, Time and Motion. Penguin Random House, San Francisco 2022, ISBN 978-0-593-18658-9, S. 145 ff. 
• Rainer Oloff: Geometrie der Raumzeit. 6. Auflage. Springer, 2018, ISBN 978-3-662-56736-4, S. 148 ff. 
• Sean M. Carroll: Spacetime and Geometry. Addison-Wesley, San Francisco 2004, ISBN 0-8053-8732-3, S. 9 ff. 

1. ↑ Wolfgang Demtröder: Experimentalphysik, Band 1: Mechanik und Wärme. 5. Auflage. Springer, Heidelberg 2008, ISBN 978-3-540-79294-9, S. 104. 
2. ↑ ^{a b} Das ganze Beispiel ist ausführlich dargestellt in: Paul Davies: About Time. Simon & Schuster, NY 1996, ISBN 978-0-684-81822-1, S. 316. 
3. ↑ French, A.P.: Die spezielle Relativitatstheorie, Vieweg + Sohn . Braunschweig, 1971, ISBN 978-3-528-03546-4
4. ↑ Albert Einstein: Zur Elektrodynamik bewegter Körper. In: Annalen der Physik. Band 322, Nr. 10, 1905, S. 891–921 (uni-augsburg.de [PDF]). 
5. ↑ Albert Einstein: Die Relativitäts-Theorie. In: Naturforschende Gesellschaft, Zürich, Vierteljahresschrift. Band 56, 1911, S. 1–14 (archive.org). 
6. ↑ Langevin, P. (1911, March). L'évolution de l'espace et du temps. In Atti del IV Congresso Internazionale di Filosofia (Vol. 1, pp. 193-214).