Das Zählmaß ist in der Mathematik ein spezielles Maß , das Mengen die Anzahl ihrer Elemente zuordnet. Formal lässt sich das Zählmaß auf einem Messraum
(
Ω
,
P
(
Ω
)
)
{\displaystyle (\Omega ,{\mathfrak {P}}(\Omega ))}
Ω
{\displaystyle \Omega }
P
(
Ω
)
{\displaystyle {\mathfrak {P}}(\Omega )}
Potenzmenge ist. Ist
Ω
{\displaystyle \Omega }
endliche Menge , so entsteht dabei ein endliches Maß . Es ist genau dann ein σ-endliches Maß, wenn
Ω
{\displaystyle \Omega }
abzählbar ist.
Definition
Das Zählmaß einer Menge
A
⊆
Ω
{\displaystyle A\subseteq \Omega }
μ
(
A
)
=
{
|
A
|
, falls
A
endlich ist,
+
∞
, falls
A
unendlich ist.
{\displaystyle \mu (A)={\begin{cases}\vert A\vert &{\text{, falls }}A{\text{ endlich ist,}}\\+\infty &{\text{, falls }}A{\text{ unendlich ist.}}\end{cases}}}
Beispiele
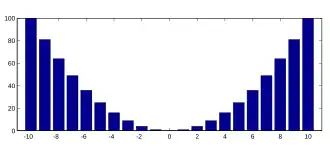
Integral der Funktion
x
↦
x
2
{\displaystyle x\mapsto x^{2}}
[
−
10
,
10
]
{\displaystyle [-10,10]}
Z
{\displaystyle \mathbb {Z} }
Über den natürlichen Zahlen , das heißt dem Messraum
(
N
,
P
(
N
)
)
{\displaystyle (\mathbb {N} ,{\mathfrak {P}}(\mathbb {N} ))}
μ
:
P
(
N
)
→
[
0
,
∞
]
,
A
↦
∑
k
∈
N
χ
A
(
k
)
.
{\displaystyle \mu \colon {\mathfrak {P}}(\mathbb {N} )\to [0,\infty ]{\text{, }}A\mapsto \sum _{k\in \mathbb {N} }\chi _{A}(k).}
Hierbei bezeichnet
χ
A
{\displaystyle \chi _{A}}
charakteristische Funktion der Menge
A
⊆
N
{\displaystyle A\subseteq \mathbb {N} }
Mit Hilfe des Zählmaßes auf
N
{\displaystyle \mathbb {N} }
Summe oder unendliche, absolut konvergente Reihe als Lebesgue-Integral darstellen. Insbesondere gilt für jede Abbildung
f
:
N
→
R
{\displaystyle f\colon \mathbb {N} \to \mathbb {R} }
∑
k
=
1
∞
f
(
k
)
{\displaystyle \sum _{k=1}^{\infty }f(k)}
konvergiert absolut
⟺
{\displaystyle \Longleftrightarrow }
f
{\displaystyle f}
integrierbar bzgl. des Zählmaßes auf
P
(
N
)
.
{\displaystyle {\mathfrak {P}}(\mathbb {N} ).}
In diesem Fall gilt
∫
N
f
d
μ
=
∑
k
=
1
∞
f
(
k
)
{\displaystyle \int _{\mathbb {N} }f\,\mathrm {d} \mu =\sum _{k=1}^{\infty }f(k)}
Literatur
Christian Hesse : Angewandte Wahrscheinlichkeitstheorie. Vieweg, Braunschweig u. a. 2003, ISBN 3-528-03183-2, S. 31.Jürgen Elstrodt : Maß- und Integrationstheorie. 4., korrigierte Auflage. Springer, Berlin u. a. 2005, ISBN 3-540-21390-2, S. 29.