Winkelhalbierendensatz (Dreieck)

Der Winkelhalbierendensatz ist eine Aussage der euklidischen Geometrie. Er besagt, dass eine Winkelhalbierende in einem Dreieck die dem Winkel gegenüberliegende Seite im Verhältnis der beiden am Winkel anliegenden Seiten teilt.
Satz und Verallgemeinerung
In einem Dreieck sei ein Punkt auf der Seite . Die Strecke teilt den Winkel in die Winkel und . Sind diese beiden Winkel gleich groß, das heißt ist die Winkelhalbierende des Winkels , dann gilt für die Streckenverhältnisse:[1]
- .
Diese Aussage lässt sich auch auf Strecken verallgemeinern, die den Winkel in einem beliebigen Verhältnis teilen. Es gilt dann die folgende Verhältnisgleichung:[2]
- .
Es gilt auch die Umkehrung des Winkelhalbierendensatzes. Das heißt, ist ein Punkt auf der Seite eines Dreiecks und gilt das Streckenverhältnis , dann ist die Winkelhalbierende des Winkels in .
Beweis

Ein einfacher Beweis der verallgemeinerten Aussage ergibt sich, indem das Flächenverhältnis der beiden durch entstandenen Teildreiecke auf zwei unterschiedliche Arten berechnet wird. Auf die erste Art ergeben sich die Dreiecksflächen nach der Formel mit Grundseite und zugehöriger Höhe , auf die zweite Art nach der Formel mit den beiden Seiten , und dem davon eingeschlossenen Winkel .
Damit erhält man nun
und
also gilt
Zu einem Beweis mit baryzentrischen Koordinaten: siehe hier.
Außenwinkelhalbierende
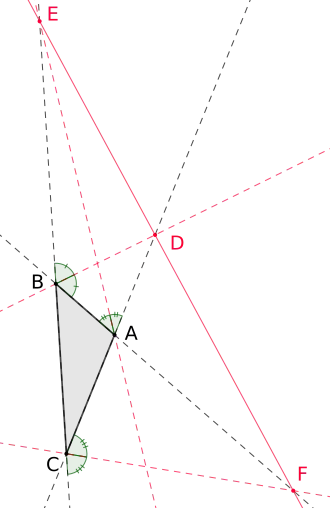
Die drei Schnittpunkte D, E, F liegen auf einer Geraden (rot) und es gelten die folgenden Streckenverhältnisse:
, ,
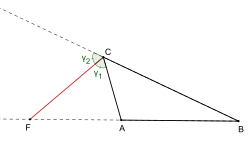
Eine ähnliche Aussage gilt für eine Außenwinkelhalbierende eines Dreiecks: Ist ein Dreieck und schneidet die Außenwinkelhalbierende in die Verlängerung der Seite in einem Punkt , so gilt für die Streckenverhältnisse
- .[3]
Es gilt auch die Umkehrung dieser Aussage. Das heißt ist ein Punkt auf der Verlängerung der Seite eines Dreiecks und gilt für die Streckenverhältnisse , dann ist die Außenwinkelhalbierende in .
Bei einem nicht gleichschenkligen Dreieck schneidet jede der drei Außenwinkelhalbierenden die Verlängerung der gegenüberliegenden Seite in einem Punkt. Sind die entsprechenden Schnittpunkte der Außenwinkelhalbierenden in , so gilt für die Streckenverhältnisse
- und .
Darüber hinaus liegen die Punkte , und auf einer gemeinsamen Geraden, sind also kollinear.[4]
Geschichte
Der Winkelhalbierendensatz findet sich in Euklids Elementen (Buch VI, Proposition 3).[5] Thomas L. Heath zufolge formulierte Robert Simson die analoge Aussage über die Außenwinkelhalbierende. Er führte weiter aus, dass Augustus de Morgan vorschlug, die beiden Aussagen in einem Satz miteinander zu verbinden.[6]
Literatur
- Siegfried Krauter, Christine Bescherer: Erlebnis Elementargeometrie: Ein Arbeitsbuch zum selbstständigen und aktiven Entdecken. Springer, 2012, ISBN 978-3-8274-3025-0, S. 161.
- Claudi Alsina, Roger B. Nelsen: Perlen der Mathematik: 20 geometrische Figuren als Ausgangspunkte für mathematische Erkundungsreisen. Springer, 2015, ISBN 978-3-662-45461-9, S. 66.
Weblinks
- proof of the angle bisector theorem (Video) bei der Khan Academy (englisch)
- angle bisector theorem auf cut-the-knot.org
- Animierter Beweis mit Drehung und dem ersten Strahlensatz (GeoGebra)
- Animierter Beweis mit Achsenspiegelung und dem zweiten Strahlensatz (GeoGebra)
Einzelnachweise
- ↑ Claudi Alsina, Roger B. Nelsen: Perlen der Mathematik: 20 geometrische Figuren als Ausgangspunkte für mathematische Erkundungsreisen. Springer, 2015, ISBN 978-3-662-45461-9, S. 66
- ↑ Titu Andreescu, Zuming Feng: 103 Trigonometry Problems: From the Training of the USA IMO Team. Springer, 2006, S. 19
- ↑ Alfred S. Posamentier: Advanced Euclidian Geometry: Excursions for Students and Teachers. Springer, 2002, ISBN 978-1-930190-85-6, S. 3–4
- ↑ Roger Arthur Johnson: Modern Geometry. An Elementary Treatise of the Geometry of the Triangle and the Circle. Houghton Mifflin Company, 1929, S. 148, Nr. 219 e. (archive.org).
- ↑ Isaac Todhunter: The Elements of Euclid, Buch VI, Proposition 3.
- ↑ Thomas L. Heath: The Thirteen Books of Euclid's Elements. 2. Auflage. Dover Publications, New York 1956.