Stabilitätsgebiet

In der Numerik gewöhnlicher Differentialgleichungen ist das Stabilitätsgebiet ${\displaystyle {\mathcal {S}}\subseteq \mathbb {C} }$ eines Verfahrens zur Lösung eines Anfangswertproblems anschaulich ein Indikator dafür, wie „pflegeleicht“ sich dieses Verfahren bei steifen Differentialgleichungen verhält.

Besonders interessant ist der Fall, wenn das Stabilitätsgebiet die komplette linke Halbebene enthält, dann heißt das Verfahren A-stabil.

Dafür betrachtet man das Verfahren beim Lösen der dahlquistschen Testgleichung

${\displaystyle y'=\lambda y,\quad \operatorname {Re} \lambda <0,}$

${\displaystyle y(t_{0})=y_{0}>0}$

für eine komplexe Zahl ${\displaystyle \lambda }$ bei fester Schrittweite ${\displaystyle h}$. Offenbar ist die analytische Lösung ${\displaystyle y(t)=y_{0}e^{\lambda t}}$.

Das Verfahren ergebe dafür die diskrete Approximation ${\displaystyle (y_{0},y_{1},\ldots )}$, also

${\displaystyle y_{n}\approx y(t_{n})}$ mit

${\displaystyle t_{n}=t_{0}+nh}$.

Ein hinreichendes Kriterium für die Stabilität ist, dass die durch das Verfahren ermittelte Näherung (genau wie die exakte Lösung) monoton fallend ist, sprich für alle ${\displaystyle n}$ die nächste Näherung maximal so groß ist wie die vorherige: ${\displaystyle |y_{n+1}|\leq |y_{n}|}$.

Ist dieses Kriterium für ein Paar ${\displaystyle (\lambda ,h)}$ erfüllt, liegt ${\displaystyle \lambda h}$ im Stabilitätsgebiet ${\displaystyle {\mathcal {S}}}$, ansonsten nicht.

Einfach berechnen lässt sich das Stabilitätsgebiet, wenn das Verfahren bezüglich der Testgleichung eine Stabilitätsfunktion ${\displaystyle R\colon \mathbb {C} \rightarrow \mathbb {C} }$ besitzt, d. h. ${\displaystyle y_{n}=\left(R(\lambda h)\right)^{n}y_{0}}$ beziehungsweise rekursiv ${\displaystyle y_{n+1}=R(\lambda h)y_{n}}$.

Da ${\displaystyle R(\lambda h)}$ per Definition nicht vom aktuellen Schritt abhängt, ist die Folge der Näherungen genau dann monoton fallend, wenn der Betrag des Faktors ${\displaystyle |R(\lambda h)|\leq 1}$ ist – und genau dann streng monoton fallend, wenn sogar ${\displaystyle |R(\lambda h)|<1}$.

Ob man das Gebiet nun strikt oder abgeschlossen definiert, unterscheidet sich, aber es ergibt sich z. B.

${\displaystyle {\mathcal {S}}:=\{z\in \mathbb {C} \mid |R(z)|<1\}}$

Alle Runge-Kutta-Verfahren haben eine Stabilitätsfunktion; bei expliziten Verfahren ist diese ein Polynom, bei impliziten wenigstens noch eine rationale Funktion, wobei die Grade jeweils durch die Schrittzahl ${\displaystyle m}$ des Verfahrens beschränkt sind.

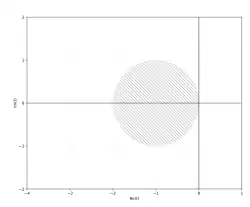
Für das explizite Euler-Verfahren gilt

${\displaystyle y_{n+1}=y_{n}+hf(t_{n},y_{n})=y_{n}+h\lambda y_{n}=(\lambda h+1)y_{n}}$,

die Stabilitätsfunktion ist daher ${\displaystyle R(z)=z+1}$. Damit liegt ${\displaystyle z}$ im Stabilitätsgebiet falls ${\displaystyle |z+1|<1}$, d. h. genau dann wenn ${\displaystyle z}$ im 1-Ball um ${\displaystyle -1\in \mathbb {C} }$ liegt. Es folgt

${\displaystyle {\mathcal {S}}=B_{1}(-1)}$.

Dieses Stabilitätsgebiet ist (wie auch jenes anderer expliziter Verfahren) beschränkt. Daher wird man, auch wenn dies die Genauigkeit gar nicht verlangen würde, zu einer Einschränkung der Schrittweite ${\displaystyle h}$ gezwungen. Dies hat zur Folge, dass implizite Verfahren beim Lösen steifer Differentialgleichungen bevorzugt werden.

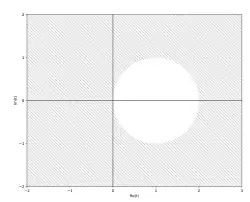
Ein Beispiel dafür ist das implizite Euler-Verfahren, das angewendet

${\displaystyle y_{n+1}=y_{n}+hf(t_{n+1},y_{n+1})=y_{n}+h\lambda y_{n+1}}$,

also nach Umstellen die Stabilitätsfunktion ${\displaystyle R(z)={\frac {1}{1-z}}}$ ergibt. Das resultiert dann im folgenden Stabilitätsgebiet und zeigt somit die A-Stabilität des Verfahrens:

${\displaystyle {\mathcal {S}}=\mathbb {C} \setminus B_{1}(1)}$

• E. Hairer, G. Wanner: Solving Ordinary Differential Equations II, Stiff problems, Springer Verlag