Soddy-Kreis

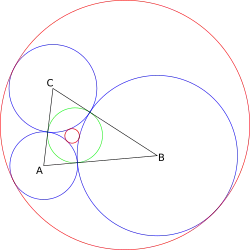
Die Soddy-Kreise sind die Lösungen für einen Spezialfall des apollonischen Problems, wobei die drei gegebenen Kreise, deren Mittelpunkte die Ecken eines Dreiecks sind, einander berühren. Sie sind benannt nach Frederick Soddy, der anhand dieser Kreise den Satz von Descartes wiederentdeckte und am 20. Juni 1936 in der Zeitschrift Nature in Form eines Gedichtes mit dem Titel The kiss precise veröffentlichte.

Gegeben seien ein Dreieck ${\displaystyle ABC}$ sowie die drei Kreise mit den Mittelpunkten ${\displaystyle A}$, ${\displaystyle B}$ bzw. ${\displaystyle C}$, die jeweils durch die Berührpunkte des Inkreises mit den anliegenden Dreiecksseiten gehen. (Diese drei Kreise berühren einander paarweise.) Die beiden Soddy-Kreise sind nun diejenigen Kreise, welche die genannten drei Kreise berühren. Im Allgemeinen unterscheidet man den inneren und den äußeren Soddy-Kreis.

• Nach dem Satz von Descartes gilt für die Krümmung ${\displaystyle k}$ der beiden Soddy-Kreise:

${\displaystyle k=k_{1}+k_{2}+k_{3}\pm 2{\sqrt {k_{1}k_{2}+k_{2}k_{3}+k_{3}k_{1}}}.}$

Hierbei bezeichnen ${\displaystyle k_{1},k_{2},k_{3}}$ die Krümmungen (= Kehrwerte der Radien) der Kreise um die Eckpunkte A, B und C.

• Der Mittelpunkt des äußeren Soddy-Kreises ist der isoperimetrische Punkt.
• Der Mittelpunkt des inneren Soddy-Kreises ist der Punkt des gleichen Umwegs.
• Für die Radien der Soddy-Kreise gilt

${\displaystyle r={\frac {A_{\triangle }}{4R+r\pm U}}.}$

Dabei bezeichnet ${\displaystyle A_{\triangle }}$ den Flächeninhalt von ${\displaystyle ABC}$, ${\displaystyle r}$ den Inkreisradius, ${\displaystyle R}$ den Umkreisradius und ${\displaystyle U}$ den Umfang. Das Pluszeichen gilt für den inneren Soddy-Kreis, das Minuszeichen für den äußeren.

• Der Radius des inneren Soddy-Kreises kann alternativ mit der Formel von W. K. B. Holz berechnet werden.
• Die Kreise um die Ecken des Dreiecks werden vom äußeren Soddy-Kreis für ${\displaystyle 4R+r<U}$ einschließend, für ${\displaystyle 4R+r>U}$ ausschließend berührt. Im Grenzfall (${\displaystyle 4R+r=U}$) ergibt sich ein unendlicher Radius, d. h. aus dem äußeren Soddy-Kreis wird eine gemeinsame Tangente.

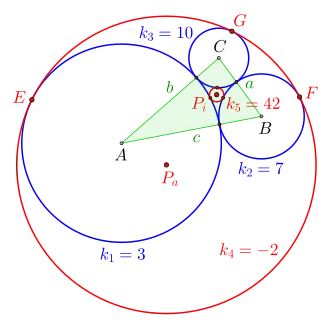
Im Folgenden wird als Beispiel eine Lösung beschrieben, in der die Krümmung der Kreise sowohl von ${\displaystyle k_{1},k_{2}}$ und ${\displaystyle k_{3}}$ als auch die der gesuchten Kreise ${\displaystyle k_{4}}$ und ${\displaystyle k_{5}}$ ganzzahlig ist.^[1] Die Konstruktion mit Zirkel und Lineal (erstellt in GeoGebra) gelingt auch für beliebige Werte von ${\displaystyle k_{1},k_{2}}$ und ${\displaystyle k_{3}}$, allerdings hat dann die Krümmung der Kreise ${\displaystyle k_{4}}$ und/oder ${\displaystyle k_{5}}$ meist einen irrationalen Wert.^[1]

Gegeben sei die Krümmung der Kreise ${\displaystyle k_{1}=3,k_{2}=7}$ und ${\displaystyle k_{3}=10}$. Wie in Eigenschaften beschrieben, ergeben sich die Kreisradien aus den Kehrwerten der entsprechenden Krümmung: ${\displaystyle r_{1}={\tfrac {1}{3}},r_{2}={\tfrac {1}{7}}}$ und ${\displaystyle r_{3}={\tfrac {1}{10}}}$.

Gesucht sind der Soddy-Kreis ${\displaystyle k_{4}}$, der die gegebenen Kreise einschließend berührt sowie der Soddy-Kreis ${\displaystyle k_{5}}$, der diese Kreise ausschließend berührt.

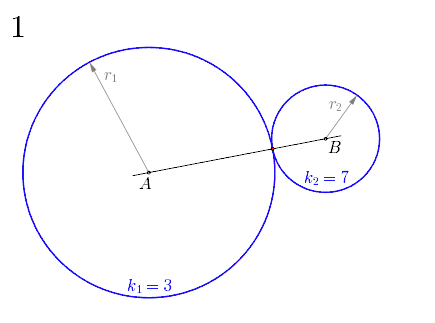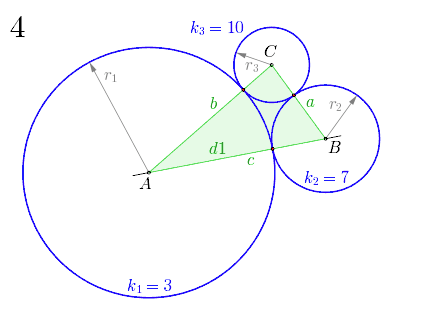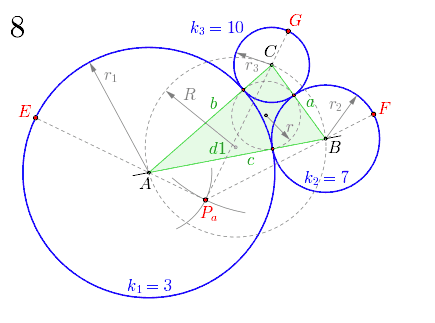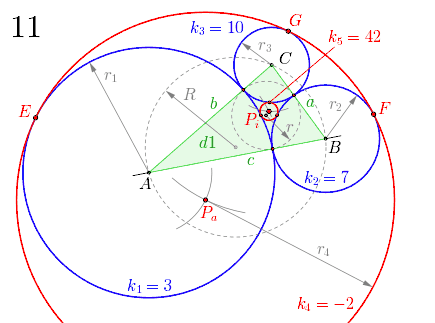
Nach dem Ziehen einer Geraden und dem Bestimmen des Punktes ${\displaystyle A}$ darauf, wird um diesen Punkt der Kreis ${\displaystyle k_{1}}$ mit dem Radius ${\displaystyle r_{1}={\tfrac {1}{3}}}$ gezogen. Anschließend wird der Punkt ${\displaystyle B}$ auf der Geraden so platziert, dass der nun folgende Kreis ${\displaystyle k_{2}}$ mit Radius ${\displaystyle r_{2}={\tfrac {1}{7}}}$ den Kreis ${\displaystyle k_{1}}$ berührt. Den Mittelpunkt ${\displaystyle C}$ für den Kreis ${\displaystyle k_{3}}$ mit Radius ${\displaystyle r_{3}={\tfrac {1}{10}}}$ erhält man als Schnittpunkt mithilfe eines Kreises mit Radius ${\displaystyle r_{6}={\tfrac {1}{3}}+{\tfrac {1}{10}}}$ sowie eines zweiten Kreises mit Radius ${\displaystyle r_{7}={\tfrac {1}{7}}+{\tfrac {1}{10}}}$. Nach dem Einzeichnen des Dreiecks ${\displaystyle \triangle {ABC}}$ (grün) mit den Seitenlängen ${\displaystyle a,b,c}$ und des Kreises ${\displaystyle k_{3}}$ wird der Mittelpunkt vom Inkreis des Dreiecks anhand der beiden Winkelhalbierenden ${\displaystyle wh_{1}}$ und ${\displaystyle wh_{2}}$ festgelegt. Jetzt kann der Inkreis mit Radius ${\displaystyle r}$ (gleich Abstand Mittelpunkt zu Berührpunkt) eingezeichnet werden. Für den Umkreises mit Radius ${\displaystyle R}$ des Dreiecks ${\displaystyle \triangle {ABC}}$ wird zuerst dessen Mittelpunkt mittels der beiden Seitenhalbierenden ${\displaystyle sh_{1}}$ und ${\displaystyle sh_{2}}$ ermittelt.

Es geht weiter mit dem Bestimmen des sogenannten isoperimetrischen Punktes ${\displaystyle P_{a}}$, das ist der Mittelpunkt des äußeren Soddy-Kreises ${\displaystyle k_{4}}$. Die hierfür benötigten Hilfskreise mit den Radien ${\displaystyle r_{8}}$ und ${\displaystyle r_{9}}$ erhält man mithilfe der in Eigenschaften beschriebenen Formel für ${\displaystyle r_{4}}$ nach Subtraktion des Radius ${\displaystyle r_{3}}$ bzw. des Radius ${\displaystyle r_{1}}$. Die Werte von ${\displaystyle A_{\triangle }(=d1),\;R,\;r,\;a,\;b,\;c}$ werden aus der GeoGebra-Konstruktion entnommen.

${\displaystyle r_{4}={\frac {A_{\triangle }}{4R+r-U}}=-0{,}5}$,

${\displaystyle r_{8}={\frac {A_{\triangle }}{4R+r-U}}-r_{3}=-0{,}4}$,

${\displaystyle r_{9}={\frac {A_{\triangle }}{4R+r-U}}-r_{1}=-0{,}1{\overline {6}}}$.

Wegen ${\displaystyle 4R+r<U}$ ergeben sich für ${\displaystyle r_{8},\;r_{9}}$ und ${\displaystyle r_{4}}$ Werte mit Minuszeichen. Für das Einzeichnen der Kreise werden die Minuszeichen bei den Radien weggelassen.

Je eine Gerade, gezogen ab ${\displaystyle P_{a}}$ durch die Ecken ${\displaystyle A,B,C}$ des Dreiecks bis zum betreffenden Kreis, erzeugt die Berührpunkte ${\displaystyle E,F}$ und ${\displaystyle G}$. Mit dem Radius ${\displaystyle |{\overline {P_{a}E}}|=r_{4}}$, wird der Soddy-Kreis mit der Krümmung ${\displaystyle k_{4}=-2}$ (entspricht ${\displaystyle {\tfrac {1}{r_{4}}}={\tfrac {1}{-0{,}5}}}$) eingezeichnet.

Nun zum zweiten Soddy-Kreis ${\displaystyle k_{4}}$ mit dessen Mittelpunkt ${\displaystyle P_{i}}$, dem sogenannten Punkt des gleichen Umwegs. Die hierfür benötigten Hilfskreise mit den Radien ${\displaystyle r_{10}}$ und ${\displaystyle r_{11}}$ erhält man mithilfe der in Eigenschaften beschriebenen Formel für ${\displaystyle r_{5}}$ nach Addition des Radius ${\displaystyle r_{3}}$ bzw. des Radius ${\displaystyle r_{1}}$. Die Werte von ${\displaystyle A_{\triangle }(=d1),\;R,\;r,\;a,\;b,\;c}$ werden aus der GeoGebra-Konstruktion entnommen.

${\displaystyle r_{5}={\frac {A_{\triangle }}{4R+r+U}}=0{,}0{\overline {238095}}={\frac {1}{42}}}$,

${\displaystyle r_{10}={\frac {A_{\triangle }}{4R+r+U}}+r_{3}=0{,}1{\overline {238095}}={\frac {13}{105}}}$,

${\displaystyle r_{11}={\frac {A_{\triangle }}{4R+r+U}}+r_{1}=0{,}3{\overline {571428}}={\frac {5}{14}}}$.

Um die Berührpunkte (ohne Bezeichnung) zu bestimmen, zieht man jeweils eine Gerade ab ${\displaystyle P_{i}}$ bis zu den Ecken ${\displaystyle A,B,C}$ des Dreiecks. Mit dem Radius ${\displaystyle r_{5}=0{,}0{\overline {238095}}={\tfrac {1}{42}}}$, gleich dem Abstand des Punktes ${\displaystyle P_{i}}$ bis zu einem Berührpunkt, wird der gesuchte Soddy-Kreis mit der Krümmung ${\displaystyle k_{5}=42}$ eingezeichnet.

• N. Dergiades: The Soddy Circles. In: Forum Geometricorum. Band 7, 2007, S. 191–197. (Online-Version)
• Eric W. Weisstein: Soddy Circles. In: MathWorld (englisch).
• Soddy Circles auf cut-the-knot
• Arthur Baragarm, Alex Kontorovich: Efficiently Constructing Tangent Circles – einfache Konstruktion der beiden Soddy-Kreise
• isoperimetric and equal detour points – interaktive Illustration auf Geogebratube
• La figure de Soddy

1. ↑ ^{a b} Richter-Gebert, Thorsten Orendt: Geometriekalküle ― 10.7 Exkurs: Apollonius und Zahlentheorie. Springer Dordrecht, Berlin Heidelberg 2009, ISBN 978-3-642-02529-7, S. 168 (springer.com).