Schnittgerade

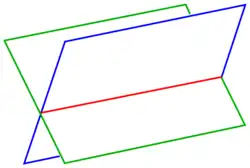
Eine Schnittgerade ist ein Begriff der Geometrie. Zwei Ebenen im dreidimensionalen euklidischen Raum, die nicht parallel zueinander sind, schneiden sich immer; die Schnittmenge ist dabei eine Gerade, die als Schnittgerade bezeichnet wird.

In der analytischen Geometrie werden Schnittgeraden – wie alle Raumgeraden – mithilfe von Gleichungen beschrieben, vorzugsweise durch Parametergleichungen. Ein typisches Problem besteht darin, eine Parametergleichung der Schnittgeraden zu bestimmen bzw. zu „berechnen“, wenn die Gleichungen der sich schneidenden Geraden gegeben sind.

Ist eine der sich schneidenden Ebenen eine Koordinatenebene, so nennt man die Schnittgerade Spurgerade.^[1] Besitzen mehrere Ebenen eine gemeinsame Schnittgerade, so spricht man von einem Ebenenbüschel.

Zwischen zwei Ebenen ${\displaystyle E_{1}}$ und ${\displaystyle E_{2}}$ im Raum können folgende Lagebeziehungen bestehen:^[2]

• ${\displaystyle E_{1}}$ und ${\displaystyle E_{2}}$ sind parallel zueinander, aber nicht gleich;
• ${\displaystyle E_{1}}$ und ${\displaystyle E_{2}}$ sind gleich;
• ${\displaystyle E_{1}}$ und ${\displaystyle E_{2}}$ sind nicht parallel zueinander und schneiden sich in einer Geraden.

Zunächst prüft man die beiden Geraden deshalb auf Nicht-Parallelität, um sicherzustellen, dass eine Schnittgerade tatsächlich existiert.

Es gibt viele Möglichkeiten, um die Parametergleichung der Schnittgeraden zu berechnen. Eine geeignete Wahl hängt unter anderem davon ab, in welcher Form (Normalenform, Parameterform) die sich schneidenden Ebenen jeweils beschrieben sind. Insgesamt lassen sich drei Fälle unterscheiden: Es können beide Ebenen als Normalenform oder als Parameterform vorliegen, oder eine Ebene liegt in Normalenform und die andere in Parameterform vor. Für jeden Fall gibt es Verfahren, die direkt an den Gleichungen der vorliegenden Ebenen ansetzen. Alternativ kann man zunächst eine oder beide Ebenengleichungen in eine andere Form umwandeln und dann eines der Verfahren für diesen Fall anwenden.

Gegeben seien eine Ebene in Normalenform,

${\displaystyle E_{1}\colon \ {\vec {n}}\cdot {\vec {x}}=d}$,

und eine Ebene in Parameterform,

${\displaystyle E_{2}\colon \ {\vec {x}}={\vec {p}}+r{\vec {u}}+s{\vec {v}}}$.

${\displaystyle E_{1}}$ und ${\displaystyle E_{2}}$ sind nicht parallel zueinander, wenn ${\displaystyle {\vec {n}}\cdot {\vec {u}}\neq 0}$ oder ${\displaystyle {\vec {n}}\cdot {\vec {v}}\neq 0}$, denn andernfalls wäre ${\displaystyle {\vec {n}}}$ auch ein Normalenvektor von ${\displaystyle E_{2}}$. Zur Bestimmung der Schnittgerade setzt man zunächst die Parametergleichung für ${\displaystyle E_{2}}$ in die Normalengleichung für ${\displaystyle E_{1}}$ ein und wendet das Distributivgesetz und Assoziativgesetz für Skalarprodukte an. Das liefert die Gleichung^[3]

${\displaystyle {\vec {n}}\cdot {\vec {p}}+r\,{\vec {n}}\cdot {\vec {u}}+s\,{\vec {n}}\cdot {\vec {v}}=d}$.

Sind die Ebenen nicht parallel, so lässt sich diese Gleichung nach ${\displaystyle r}$ oder nach ${\displaystyle s}$ auflösen. Mit der dadurch erhaltenen Gleichung lässt sich ein Parameter in der Gleichung für ${\displaystyle E_{2}}$ eliminieren, wodurch man zu einer Parametergleichung für die Schnittgerade gelangt.

Die beiden Ebenen seien gegeben durch

${\displaystyle E_{1}\colon \ {\begin{pmatrix}1\\2\\1\end{pmatrix}}\cdot {\vec {x}}=1}$

und

${\displaystyle E_{2}\colon \ {\vec {x}}={\begin{pmatrix}1\\1\\1\end{pmatrix}}+r{\begin{pmatrix}2\\1\\-3\end{pmatrix}}+s{\begin{pmatrix}-1\\1\\0\end{pmatrix}}}$.

Es ist ${\displaystyle (1,2,1)^{T}\cdot (2,1,-3)^{T}\neq 0}$ und ${\displaystyle (1,2,1)^{T}\cdot (-1,1,0)^{T}\neq 0}$, also sind ${\displaystyle E_{1}}$ und ${\displaystyle E_{2}}$ nicht parallel zueinander. Einsetzen der Parametergleichung in die Normalengleichung liefert

${\displaystyle {\begin{pmatrix}1\\2\\1\end{pmatrix}}\cdot \left[{\begin{pmatrix}1\\1\\1\end{pmatrix}}+r{\begin{pmatrix}2\\1\\-3\end{pmatrix}}+s{\begin{pmatrix}-1\\1\\0\end{pmatrix}}\right]=1}$.

Diese Gleichung liest sich nach Anwendung der Rechengesetze für das Skalarprodukt als

${\displaystyle {\begin{pmatrix}1\\2\\1\end{pmatrix}}\cdot {\begin{pmatrix}1\\1\\1\end{pmatrix}}+r{\begin{pmatrix}1\\2\\1\end{pmatrix}}\cdot {\begin{pmatrix}2\\1\\-3\end{pmatrix}}+s{\begin{pmatrix}1\\2\\1\end{pmatrix}}\cdot {\begin{pmatrix}-1\\1\\0\end{pmatrix}}=1}$.

Ausrechnen der Skalarprodukte und Umstellen liefert ${\displaystyle s=-3-r}$. Damit lässt sich ${\displaystyle s}$ in der Parametergleichung für ${\displaystyle E_{2}}$ eliminieren:

${\displaystyle {\vec {x}}={\begin{pmatrix}1\\1\\1\end{pmatrix}}+r{\begin{pmatrix}2\\1\\-3\end{pmatrix}}+(-3-r){\begin{pmatrix}-1\\1\\0\end{pmatrix}}}$.

Nach Anwendung der Rechenregeln für Vektoren erhält man hieraus schließlich eine Parameterdarstellung für die Schnittgerade:

${\displaystyle g\colon \ {\vec {x}}={\begin{pmatrix}-5\\-2\\10\end{pmatrix}}+r{\begin{pmatrix}-3\\0\\3\end{pmatrix}}}$.

Gegeben seien zwei Ebenen

${\displaystyle E_{1}\colon \ {\vec {x}}={\vec {p}}_{1}+r{\vec {u}}_{1}+s{\vec {v}}_{1}\quad }$und ${\displaystyle \quad E_{2}\colon \ {\vec {x}}={\vec {p}}_{2}+r{\vec {u}}_{2}+s{\vec {v}}_{2}}$.

Um die Parallelität der beiden Ebenen zu untersuchen, bestimmt man zunächst mit Hilfe des Kreuzproduktes für eine der Ebenen einen Normalenvektor. Sind die Skalarprodukte dieses Normalenvektors mit den Richtungsvektoren der anderen Ebene jeweils ungleich null, so sind die beiden Ebenen nicht parallel. Alternativ kann man auch für beide Ebenen einen Normalenvektor bestimmen. Zeigen die beiden Normalenvektoren in verschiedene Richtungen, sind also keine Vielfachen voneinander, so sind die beiden Ebenen nicht parallel zueinander.

Der direkte Weg zur Bestimmung der Schnittgeraden besteht darin, die beiden Parametergleichungen gleichzusetzen:^[4]

${\displaystyle {\vec {p}}_{1}+r_{1}{\vec {u}}_{1}+s_{1}{\vec {v}}_{1}={\vec {p}}_{2}+r_{2}{\vec {u}}_{2}+s_{2}{\vec {v}}_{2}}$.

Diese Vektorgleichung lässt sich in ein lineares 3×4 Gleichungssystem in den Unbekannten ${\displaystyle r_{1},r_{2},s_{1},s_{2}}$ übersetzen, welches sich auf eine Gleichung in zwei Variablen zurückführen lässt. Damit kann man beispielsweise den Parameter ${\displaystyle r_{2}}$ in Abhängigkeit von ${\displaystyle s_{2}}$ ausdrücken und in der Ebenengleichung für ${\displaystyle E_{2}}$ ersetzen. Dadurch gelangt man nach elementaren Vektorumformungen zu einer Parametergleichung der Schnittgeraden.

Die beiden Ebenen seien gegeben durch

${\displaystyle E_{1}\colon \ {\vec {x}}={\begin{pmatrix}1\\-1\\1\end{pmatrix}}+r_{1}{\begin{pmatrix}2\\1\\-1\end{pmatrix}}+s_{1}{\begin{pmatrix}-1\\1\\0\end{pmatrix}}\quad }$ und ${\displaystyle \quad E_{2}\colon \ {\vec {x}}={\begin{pmatrix}1\\1\\1\end{pmatrix}}+r_{2}{\begin{pmatrix}2\\2\\-1\end{pmatrix}}+s_{2}{\begin{pmatrix}1\\0\\1\end{pmatrix}}}$.

Durch Gleichsetzen und Umformen erhält man das Gleichungssystem

${\displaystyle {\begin{matrix}&-2r_{1}&-&2r_{2}&-&s_{1}&-&s_{2}&=&5\\&r_{1}&-&2r_{2}&+&s_{1}&&&=&5\\&-r_{1}&+&r_{2}&&&&-s_{2}&=&0\end{matrix}}}$

Es hat eine einparametrige Lösungsschar. Wählt man z. B. ${\displaystyle s_{2}=t}$ als freien Parameter, so ist ${\displaystyle r_{2}=-2-4t}$. Einsetzen in die Parametergleichung für ${\displaystyle E_{2}}$ ergibt

${\displaystyle {\vec {x}}={\begin{pmatrix}1\\1\\1\end{pmatrix}}+(-2-4t){\begin{pmatrix}2\\2\\-1\end{pmatrix}}+t{\begin{pmatrix}1\\0\\1\end{pmatrix}}}$.

Nach Anwendung der Rechenregeln für Vektoren erhält man hieraus für die Schnittgerade die Parameterdarstellung

${\displaystyle g\colon \ {\vec {x}}={\begin{pmatrix}-3\\-3\\3\end{pmatrix}}+t{\begin{pmatrix}-7\\-8\\5\end{pmatrix}}}$.

Gegeben seien zwei Ebenen

${\displaystyle E_{1}\colon \ {\vec {n}}_{1}\cdot {\vec {x}}=d_{1}\quad }$ und ${\displaystyle \quad E_{2}\colon \ {\vec {n}}_{2}\cdot {\vec {x}}=d_{2}}$.

${\displaystyle E_{1}}$ und ${\displaystyle E_{2}}$ sind nicht parallel zueinander, wenn die beiden Normalenvektoren ${\displaystyle {\vec {n}}_{1},{\vec {n}}_{2}}$ in verschiedene Richtungen zeigen, also keine Vielfachen voneinander sind.

Die beiden Normalengleichungen liefern ein lineares 2×3 Gleichungssystem mit den Koordinaten ${\displaystyle x,y,z}$ als Unbekannten. Um dieses unterbestimmte Gleichungssystem zu lösen, wird es zunächst auf Zeilenstufenform gebracht und eine der Unbekannten der untersten Zeile als Parameter gesetzt; die anderen beiden Koordinaten lassen sich dann in Abhängigkeit dieses Parameters ausdrücken. Wendet man auf den Lösungsvektor, dessen Komponenten nun alle in Abhängigkeit des Parameters ausgedrückt sind, elementare Rechengesetzt für Vektoren an, so gelangt man zu einer Parametergleichung der Schnittgeraden.

Die beiden Ebenen seien gegeben durch

${\displaystyle E_{1}\colon \ {\begin{pmatrix}1\\2\\1\end{pmatrix}}\cdot {\vec {x}}=1\quad }$und ${\displaystyle \quad E_{2}\colon \ {\begin{pmatrix}2\\-3\\2\end{pmatrix}}\cdot {\vec {x}}=2}$.

Die Normalenvektoren ${\displaystyle (1,2,1)^{T}}$ und ${\displaystyle (2,-3,2)^{T}}$ sind keine Vielfachen voneinander, also sind ${\displaystyle E_{1}}$ und ${\displaystyle E_{2}}$ nicht parallel zueinander und haben eine Schnittgerade. Deren Punkte ${\displaystyle {\vec {x}}=(x,y,z)^{T}}$ erfüllen das lineare Gleichungssystem

${\displaystyle {\begin{matrix}&x&+&2y&+&z&=&1\\&2x&-&3y&+&2z&=&2\end{matrix}}}$

2-mal die erste Gleichung minus 1-mal die zweite Gleichung ergibt das Gleichungssystem in Zeilenstufenform:

${\displaystyle {\begin{matrix}&x&+&2y&+&z&=&1\\&&&7y&&&=&0\end{matrix}}}$

Die Unbekannte ${\displaystyle z}$ kann frei gewählt werden: ${\displaystyle z=t}$. Nachdem ${\displaystyle y=0}$ ist, liefert ein Einsetzen in die erste Gleichung ${\displaystyle x=1-t}$. Also lassen sich alle Lösungsvektoren schreiben als ${\displaystyle {\vec {x}}=(1-t,0,t)^{T}}$, woraus man schließlich für die Schnittgerade die Parameterdarstellung erhält:

${\displaystyle {\vec {x}}={\begin{pmatrix}1\\0\\0\end{pmatrix}}+t{\begin{pmatrix}-1\\0\\1\end{pmatrix}}}$.

Da die Schnittgerade in beiden Ebenen liegt, stehen die beiden Normalenvektoren ${\displaystyle {\vec {n}}_{1}}$ und ${\displaystyle {\vec {n}}_{2}}$ senkrecht auf dem Richtungsvektor der Schnittgeraden. Als Richtungsvektor ${\displaystyle {\vec {u}}}$ der Schnittgeraden kann somit das Kreuzprodukt der Normalenvektoren genutzt werden: ${\displaystyle {\vec {u}}={\vec {n}}_{1}\times {\vec {n}}_{2}}$.^[5] Für den Stützvektor ${\displaystyle {\vec {p}}}$ betrachtet man den Schnittpunkt der Ebenen ${\displaystyle E_{1}}$, ${\displaystyle E_{2}}$ und

${\displaystyle E_{3}\colon \ {\vec {x}}=r{\vec {n}}_{1}+s{\vec {n}}_{2}}$.

Er liegt in allen drei Ebenen und somit auch auf der Schnittgeraden von ${\displaystyle E_{1}}$ und ${\displaystyle E_{2}}$. Somit lässt sich sein Ortsvektor ${\displaystyle {\vec {p}}}$ als Stützvektor verwenden. Da ${\displaystyle {\vec {p}}}$ insbesondere in ${\displaystyle E_{3}}$ liegt, lässt er sich schreiben als ${\displaystyle {\vec {p}}=r_{0}{\vec {n}}_{1}+s_{0}{\vec {n}}_{2}}$. Um die Parameter ${\displaystyle r_{0}}$ und ${\displaystyle s_{0}}$ zu finden, setzt man die Gleichung für ${\displaystyle E_{3}}$ in die Gleichungen für ${\displaystyle E_{1}}$ und ${\displaystyle E_{2}}$ ein und wendet das Distributivgesetz und Assoziativgesetz für Skalarprodukte an. Das führt auf das lineare 2×2 Gleichungssystem

${\displaystyle {\begin{matrix}&r\ {\vec {n}}_{1}\cdot {\vec {n}}_{1}&+&s\ {\vec {n}}_{1}\cdot {\vec {n}}_{2}&=&d_{1}\\&r\ {\vec {n}}_{1}\cdot {\vec {n}}_{2}&+&s\ {\vec {n}}_{2}\cdot {\vec {n}}_{2}&=&d_{2}\end{matrix}}}$

in den Unbekannten ${\displaystyle r}$ und ${\displaystyle s}$. Auflösen und Einsetzen der eindeutigen Lösung ${\displaystyle (r_{0},s_{0})}$ in die Gleichung für ${\displaystyle {\vec {p}}}$ liefert den Stützvektor. Schließlich werden noch der Richtungsvektor und der Stützvektor zur Parametergleichung verbunden.

Für die Ebenen aus dem letzten Beispiel erhält man den Richtungsvektor der Schnittgerade als

${\displaystyle {\vec {u}}={\begin{pmatrix}1\\2\\1\end{pmatrix}}\times {\begin{pmatrix}2\\-3\\2\end{pmatrix}}={\begin{pmatrix}7\\0\\-7\end{pmatrix}}}$.

Für den Stützvektor ${\displaystyle {\vec {p}}}$ erhält man mit ${\displaystyle {\vec {n}}_{1}\cdot {\vec {n}}_{1}=6,\ {\vec {n}}_{2}\cdot {\vec {n}}_{2}=17,\ {\vec {n}}_{1}\cdot {\vec {n}}_{2}=-2}$ das lineare Gleichungssystem

${\displaystyle {\begin{matrix}&6r&+&-2s&=&1\\&-2r&+&17s&=&2\end{matrix}}}$

Es hat die eindeutige Lösung ${\displaystyle r_{0}=3/14,\ s_{0}=2/14}$. Damit erhält man den Stützvektor

${\displaystyle {\vec {p}}={\frac {3}{14}}{\begin{pmatrix}1\\2\\1\end{pmatrix}}+{\frac {2}{14}}{\begin{pmatrix}2\\-3\\2\end{pmatrix}}={\begin{pmatrix}1/2\\0\\1/2\end{pmatrix}}}$.

Also ist

${\displaystyle g\colon \ {\vec {x}}={\begin{pmatrix}1/2\\0\\1/2\end{pmatrix}}+t{\begin{pmatrix}7\\0\\-7\end{pmatrix}}}$

eine (etwas andere) Parameterdarstellung der Schnittgerade beider Ebenen.

• Schnittkurve
• Schnittpunkt
• Schnittwinkel (Geometrie)
• Lagebeziehung

• Michael Jung: Ebene Trigonometrie & Analytische Geometrie. Springer Spektrum, Wiesbaden 2024, ISBN 978-3-658-03261-6, S. 594–611.
• Schülerduden Die Mathematik II (11.–13. Schuljahr). 3. Auflage. Dudenverlag, Mannheim / Wien / Zürich 1991, ISBN 3-411-04273-7, S. 89–90.
• Gerhard Merziger, Thomas Wirth: Repetitorium höhere Mathematik. 6. Auflage. Binomi-Verl, Barsinghausen 2010, ISBN 978-3-923923-34-2, S. 154–155.
• Lehr- und Übungsbuch Mathematik Band III. 15. Auflage. Verlag Harri Deutsch, Thun 1978, ISBN 978-3-87144-041-0, S. 188–189.
• Steffen Goebbels, Stefan Ritter: Mathematik verstehen und anwenden: Differenzial- und Integralrechnung, Lineare Algebra. 4. Auflage. Springer Spektrum, 2023, ISBN 978-3-662-68366-8, S. 533–534.

1. ↑ Schülerduden Die Mathematik II. 1991, S. 89. 
2. ↑ Goebbels, Ritter: Mathematik verstehen und anwenden: Differenzial- und Integralrechnung, Lineare Algebra. 2023, S. 533. 
3. ↑ Jung: Ebene Trigonometrie & Analytische Geometrie. 2024, S. 605. 
4. ↑ Schülerduden Die Mathematik II (11.–13. Schuljahr). 1991, S. 89. 
5. ↑ Jung: Ebene Trigonometrie & Analytische Geometrie. S. 603.