Schiffler-Punkt

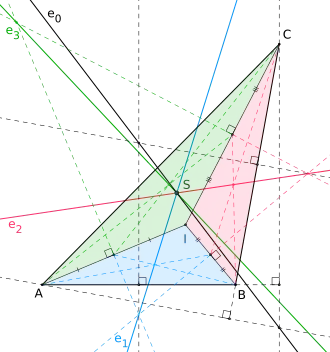
Der Schiffler-Punkt ist einer der besonderen Punkte eines Dreiecks und hat die Kimberling-Nummer X(21). Ist I der Mittelpunkt des Inkreises, so schneiden sich die eulerschen Geraden der Dreiecke ABC, BCI, CAI und ABI in einem Punkt. Dieser Schnittpunkt wurde 1985 von dem Spielwarenfabrikanten und Amateurgeometer Kurt Schiffler in der kanadischen Mathematikzeitschrift Crux Mathematicorum eingeführt und wird heute als Schiffler-Punkt bezeichnet und die Aussage, dass sich alle vier Eulergeraden in jenem Punkt schneiden, als Satz von Schiffler.^[1][2]

Die trilinearen Koordinaten des Schiffler-Punkts (${\displaystyle X_{21}}$) sind (gleichwertig)

${\displaystyle {\frac {b+c-a}{b+c}}\,:\,{\frac {c+a-b}{c+a}}\,:\,{\frac {a+b-c}{a+b}}}$ oder

${\displaystyle {\frac {1}{\cos \beta +\cos \gamma }}\,:\,{\frac {1}{\cos \gamma +\cos \alpha }}\,:\,{\frac {1}{\cos \alpha +\cos \beta }}}$.^[3]

Die baryzentrischen Koordinaten sind (gleichwertig)

${\displaystyle {\frac {a(s-a)}{b+c}}\,:\,{\frac {b(s-b)}{c+a}}\,:\,{\frac {c(s-c)}{a+b}}}$ oder

${\displaystyle {\frac {a}{\cos \beta +\cos \gamma }}\,:\,{\frac {b}{\cos \gamma +\cos \alpha }}\,:\,{\frac {c}{\cos \alpha +\cos \beta }}}$.^[3]

Dabei sind ${\displaystyle a,b,c}$ die Seitenlängen des Dreiecks und ${\displaystyle \alpha ,\beta ,\gamma }$ die Größen der Innenwinkel. ${\displaystyle s={\tfrac {a+b+c}{2}}}$ bezeichnet den halben Umfang.

• Eric W. Weisstein: Schiffler Point. In: MathWorld (englisch).

1. ↑ Joe Goggins: The Converse of Schiffler’s theorem. In: Crux Mathematicorum, with Mathematical Mayhem, Canadian Mathematical Society, 2007, Band 33, Nr. 6, S. 354, cms.math.ca (PDF)
2. ↑ Kurt Schiffler: Problem 1018. In: Crux Mathematicorum, Band 11, Nr. 2, Februar 1985, S. 51, cms.math.ca (PDF). G. R. Veldkamp, W. A. van der Spek: Solutions to Problem 1018. In: Crux Mathematicorum, Band 12, Nr. 6, Juni 1986, S. 151, cms.math.ca (PDF)
3. ↑ ^{a b} Clark Kimberling: Enyclopedia of Triangle Centers, X(21). Abgerufen am 28. Januar 2025 (englisch).