Satz des arktischen Kreises
Der Satz des arktischen Kreises (englisch arctic circle theorem) ist ein Resultat aus der Stochastik und der Kombinatorik, der sagt, dass bei einer zufälligen Parkettierung großer aztekischer Diamanten durch Dominosteine, das Muster außerhalb einer Kreisregion gefriert. Die Parkettierung wird dabei unter der Gleichverteilung gezogen, der Kreis wird arktischer Kreis genannt und ist ein Phasenübergang. Das darunterliegende Gesetz gehört zu den sogenannten universellen Gesetzen der Stochastik.
Der Satz wurde 1995 von William Jockusch, James Propp und Peter Shor bewiesen.[1] 2002 zeigt dann Kurt Johansson, dass die Fluktuation des Randes um den arktischen Kreis zum sogenannten Airy-Prozess konvergiert, welcher der Tracy-Widom-Verteilung des GUE aus der Theorie der zufälligen Matrizen folgt.[2] Die Verteilung beschreibt dort das Verhalten des größten Eigenwerts. Die Parkettierung des aztekischen Diamanten mit Dominosteinen kann als zufälliges Wachstumsmodell (englisch random growth model) aufgefasst werden und gehört zur KPZ-Universalitätsklasse.
Einführung
Zuerst müssen einige Begriffe wie Zelle, Dominostein, aztekischer Diamant und Dominostein-Parkettierung (auch Domino-Tiling oder Domino-Tessellation genannt) eingeführt werden. Für das Verständnis empfiehlt es sich die Grafiken zu betrachten.
Begriffe
Ein ganzzahliges Quadratgitter der Form mit nennt man Zelle, das sind also Quadrate in mit Ecken in . Beispielsweise hat die Zelle die Eckpunkte . Die Vereinigung zweier nebeneinanderliegenden Zellen nennt man Dominostein, entweder horizontal als -Dominostein oder vertikal als -Dominostein.
Ein aztekischer Diamant der Ordnung besteht aus der Vereinigung aller Zellen , welche komplett in der Region liegen. Dies sind exakt Zellen und man kann den aztekischen Diamant auch als folgende Menge schreiben[3]
Eine Dominostein-Parkettierung des aztekischen Diamant entsteht, wenn man den aztekischen Diamant mit nicht überlappenden Dominos vollständig überdeckt (englisch tiling), dabei können sowohl als auch -Steine verwendet werden.
-
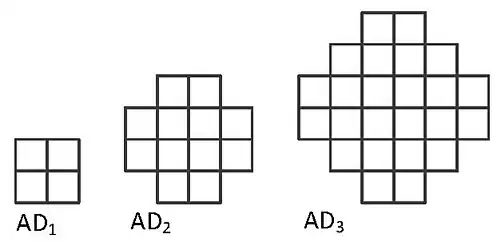 Aztekische Diamanten der Ordnung , und
Aztekische Diamanten der Ordnung , und -
 Ein aztekischer Diamant der Ordnung
Ein aztekischer Diamant der Ordnung -
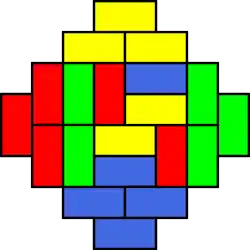 Eine Domino-Parkettierung
Eine Domino-Parkettierung -
 Die vier Typen von Dominosteinen mit ihren Höhenfunktionen (rot). (W) = West, (E) = Ost, (S) = Süd, (N) = Nord
Die vier Typen von Dominosteinen mit ihren Höhenfunktionen (rot). (W) = West, (E) = Ost, (S) = Süd, (N) = Nord
Nord-, West-, Süd- und Ost-Steine
Statt mit nur Typen von Dominosteinen zu arbeiten, werden wir eine weitere Struktur einführen, welche die Dominosteine in weitere Klassen unterteilt. Hierfür legt man ein Schachbrett über den aztekischen Diamanten, das heißt, die Zellen sind abwechselnd schwarz oder weiß. Dadurch erhält man verschiedene Typen von Dominosteine, je nachdem, ob sie horizontal oder vertikal liegen und wo sich die schwarze respektive weiße Zelle befindet. Diese Typen sind in der oben dargestellten Parkettierung mit Farben dargestellt.
Horizontale Dominosteine werden als Nord-Dominosteine (N) bezeichnet, wenn deren linkes Quadrat weiß ist, und als Süd-Dominosteine (S), wenn deren linkes Quadrat schwarz ist. Vertikale Dominosteine werden als West-Dominosteine (W) bezeichnet, wenn deren oberes Quadrat weiß ist, und als Ost-Dominosteine (E), wenn deren oberes Quadrat schwarz ist.[4] In der Grafik oben sind die Nordsteine gelb, die Südsteine blau, die Weststeine rot und die Oststeine grün.
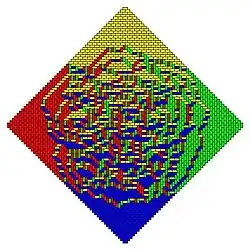
Der arktische Kreis und die Polarregion
Interessanterweise entstehen Regionen in den Ecken des aztekischen Diamanten, welche jeweils nur aus einem Typ Dominostein bestehen, und welche durch einen inneren Kreis abgegrenzt sind. Dieser Kreis wird arktischer Kreis genannt und je größer die Ordnung ist, desto besser sieht man die Kreisform. Der arktische Kreis unterteilt den aztekischen Diamanten in zwei Regionen, die innere Region heißt gemäßigte Region und diejenige außerhalb des Kreises nennt man Polarregion, da dort in einer Ecke nur ein Typ von Dominostein vorkommt und die Steine „gefroren“ scheinen. Entsprechend nennt man die Polarregion, welche durch die Nord-Dominosteine gebildet wird, die Nordpolarregion und auf analoge Weise bezeichnet man die anderen Polarregionen entsprechend der Steine, welche die Region bilden. Der innere Kreis von wird definiert als der innere Kreis in der Mitte von , welcher den Radius besitzt.
Kombinatorik und Wahrscheinlichkeitstheorie
Die Menge der möglichen Domino-Parkettierungen von sei mit notiert. Für die Anzahl gilt .[5] Für eine Parkettierung sei mit die Anzahl vertikaler Dominosteine notiert.
Eine zufällige Parkettierung ist eine Parkettierung, die unter einer Wahrscheinlichkeitsverteilung gezogen wurde. Die Gleichverteilung ist durch die Wahrscheinlichkeitsfunktion definiert und sei mit notiert. Wir können ein Wahrscheinlichkeitsmaß auch mit Hilfe der Dominosteine konstruieren und geben hierfür den Dominosteinen ein Gewicht. Den horizontalen Dominosteinen wird jeweils das Gewicht zugeteilt und den vertikalen Dominosteinen das Gewicht . Dann kann man ein Maß wie folgt konstruieren:
Wenn man den vertikalen Dominosteinen das Gewicht zuteilt, dann erhält man wieder die Gleichverteilung. Um den arktischen Kreis zu erhalten, benötigt man , ansonsten erhält man die arktische Ellipse.
Höhenfunktion und daraus resultierende Pfade
Zu jedem Dominostein wird nun eine Höhenfunktionen eingeführt, das heißt eine Linie wird auf die Steine gezeichnet. Für die horizontale Dominostein seien zwei Ecken in und . Dann zieht man für die West-Steine eine Linie von nach und für die Ost-Steine von nach . Für die vertikalen Dominostein seien zwei Ecken in und . Dann zieht man für die Süd-Steine eine Linie von nach und für den Nordstein zieht man keine Linie. Die Höhenfunktionen sind in der Grafik oben in rot ersichtlich. Beachte, dass die Konstruktion der Linien im Zusammenhang mit dem zugrundeliegenden Schachbrettmuster zu zusammenhängenden Linien zwischen den Rändern führt.
Dadurch entstehen Pfade von der westlichen Seite durch den aztekischen Diamanten auf die östliche Seite, welch sich nicht kreuzen, und eine Verbindung zur Theorie der stochastischen Prozess. Da die Nordsteine keine Linie haben, gibt es keinen Pfad durch die Nordpolarregion (gelb). Die Pfade gehen von nach für . Der nördlichste Pfad erhält man für , er geht von nach und kann als Pfad verstanden werden, das heißt bildet ein stochastischer Prozess, wobei die Ordnung des Diamanten und die Zeit ist. Der zugrundeliegende Prozess wird Nordpolarregion-Grenzprozess („NPR-Grenzprozess“) genannt. Die Nordpolarregion besteht aus all diesen Nord-Dominosteinen, welche über liegen.[6]
Der Satz des arktischen Kreises
Der Satz des arktischen Kreises lautet wie folgt:
- Sei der aztekische Diamant der Ordnung . Sei fix, dann existiert ein so dass für alle jede zufällige Parkettierung von mit Wahrscheinlichkeit eine gemäßigte Region hat, deren Rand gleichmäßig innerhalb eines Abstands von zum inneren Kreises mit Radius bleibt.[7]
Der Satz sagt also, dass wenn groß genug ist, nahezu alle zufällig gewählten Domino-Parkettierungen eine gemäßigte Region haben, deren Rand innerhalb des kleinen Abstands von zum inneren Kreis mit Radius bleiben. Der Rand der gemäßigten Region kann außerhalb des Kreises liegen, er ist aber in der Nähe des Kreises. Dieses Ereignis geschieht mit der Wahrscheinlichkeit und je größer ist, desto kleiner kann gewählt werden.
Resultat von Johansson
Das Resultat von Johansson lautet wie folgt:
- Sei der oben definierte NPR-Grenzprozess und sei der Airy2-Prozess, und weiter sei das Gewicht der vertikalen Dominosteine . Dann konvergiert
- in Verteilung wenn , im Sinne der endlichdimensionalen Verteilungen.[8]
Damit ist gemeint, dass für jede endliche Auswahl von Zeitpunkten der Prozess gegen konvergiert.
Einzelnachweise
- ↑ William Jockusch, James Propp und Peter Shor: Random domino tilings and the arctic circle theorem. 1995, arxiv:math/9801068v1.
- ↑ Kurt Johansson: The arctic circle boundary and the airy process. In: Institute of Mathematical Statistics (Hrsg.): The Annals of Probability. Band 33, Nr. 1, 2005, S. 1–30, doi:10.1214/009117904000000937.
- ↑ Dan Romik: Arctic circles, domino tilings and square Young tableaux. In: Ann. Probab. Band 40, Nr. 2, 2012, S. 611 - 647, doi:10.1214/10-AOP628.
- ↑ a b Kurt Johansson: The arctic circle boundary and the airy process. In: Institute of Mathematical Statistics (Hrsg.): The Annals of Probability. Band 33, Nr. 1, 2005, S. 1, doi:10.1214/009117904000000937.
- ↑ Elkies, G.; Kuperberg, M.; Larsen, J.; Propp, J.: Alternating sign matrices and domino tilings. In: Journal of Algebraic Combinatorics. Band 1, Nr. 2, 1992, S. 111–132 und 219–234.
- ↑ Kurt Johansson: The arctic circle boundary and the airy process. In: Institute of Mathematical Statistics (Hrsg.): The Annals of Probability. Band 33, Nr. 1, 2005, S. 2, doi:10.1214/009117904000000937.
- ↑ William Jockusch, James Propp und Peter Shor: Random domino tilings and the arctic circle theorem. 1995, S. 2.
- ↑ Kurt Johansson: The arctic circle boundary and the airy process. In: Institute of Mathematical Statistics (Hrsg.): The Annals of Probability. Band 33, Nr. 1, 2005, S. 3, doi:10.1214/009117904000000937.