STO-NG-Basissätze
STO-NG-Basissätze sind minimale Basissätze, die in der Computerchemie verwendet werden, um im Rahmen der Hartree-Fock-Theorie oder Dichtefunktionaltheorie die Molekülorbitale von chemischen Systemen zu bestimmen. Die Basisfunktionen sind dabei Slater-Orbitale („Slater-type orbitals“, STOs), die jeweils durch N primitive Gauß’sche-Orbitale („Gaussian-type Orbitals“, GTOs) angenähert werden.[1] STO-NG-Basissätze wurden zunächst von John Pople entwickelt. N nimmt typischerweise Werte von 2 – 6 an.[1] Ein minimaler Basissatz zeichnet sich dadurch aus, dass es aus nur so vielen Orbitalen besteht wie nötig sind, um jedes Atom im freien, neutralen Zustand beschreiben zu können. Das heißt, dass für das Wasserstoffatom nur ein einziges 1s-Orbital benötigt wird, während für ein Kohlenstoffatom jeweils ein 1s, 2s und drei 2p-Orbitale benötigt werden.
Allgemeine Definition
STO-NG Basissätze bestehen aus einem STO (mit geeignetem Parameter ) für jedes Orbital des freien, neutralen Atoms und für jedes Atom im betrachteten System (z. B. ein Molekül). Die STOs sind um den Kern des Atoms zentriert, dem sie zugeordnet sind. Folglich ist die Anzahl der Basisfunktionen, die einem Atom zugeordnet sind, abhängig des Elements. Die STO-NG Basissätze sind für alle Atome von Wasserstoff bis Xenon verfügbar.[2]
| Element | Anzahl an STOs | STOs |
|---|---|---|
| H, He | 1 | 1s |
| Li, Be | 2 | 1s, 2s |
| B, C, N, O, F, Ne | 5 | 1s, 2s, 2p |
| Na, Mg | 6 | 1s, 2s, 2p, 3s |
| Al, Si, P, S, Cl, Ar | 9 | 1s, 2s, 2p, 3s, 3p |
| K, Ca | 10 | 1s, 2s, 2p, 3s, 3p, 4s |
| Sc-Zn | 15 | 1s, 2s, 2p, 3s, 3p, 4s, 3d |
| Ga-Kr | 18 | 1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p |
| Rb, Sr | 19 | 1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s |
| Y-Cd | 24 | 1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d |
| In-Xe | 27 | 1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p |
Jedes STO (sowohl innere als auch Valenzorbitale) , mit die Hauptquantenzahl und die Drehimpuls-Quantenzahl, iwird durch eine Linearkombination aus primitiven GTOs mit Exponenten approximiert:[3]
Die Koeffizienten und Exponenten werden mit Hilfe der Methode der kleinsten Quadrate an alle STOs innerhalb der gleichen Schale gleichzeitig angepasst. Dies unterscheidet sich von dem üblicheren Verfahren, bei dem sie so gewählt werden, dass die Energie des Moleküls minimiert wird. Es sei außerdem angemerkt, dass alle innerhalb derselben Schale (z. B. 2s und 2p) die gleichen Exponenten aufweisen, d. h. die Exponenten hängen nicht von ab, was ein typisches Merkmal dieses Basissatzes ist und eine effizientere Berechnung ermöglicht.[4]
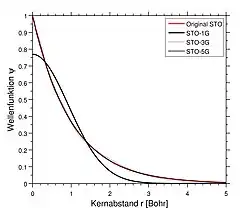
Die Approximation der STOs durch GTOs ist oft akzeptabel außer bei s Orbitalen in der Nähe des Kerns: Dort weisen STOs eine Spitze auf, während GTOs flach sind.[5][6] Die Werte der Parameter für s bis g Orbitale in den STO-1G bis STO-6G Basissätzen wurden ausführlich tabelliert[7] und die Atom-spezifischen Parameter für die STO-2G bis STO-6G Basissätze können auf Basis Set Exchange[8] vorgefunden werden.
STO-2G
Der STO-2G-Basissatz ist eine Linearkombination von zwei primitiven Gauß-Funktionen. Die ursprünglichen Koeffizienten und Exponenten für Atome der ersten und der zweiten Periode sind wie folgt gegeben (für ).[4]
| STO-2G | α1 | c1 | α2 | c2 |
| 1s | 0.151623 | 0.678914 | 0.851819 | 0.430129 |
| 2s | 0.0974545 | 0.963782 | 0.384244 | 0.0494718 |
| 2p | 0.0974545 | 0.61282 | 0.384244 | 0.511541 |
Für allgemeine Werte von kann das Skalierungsgesetz genutzt werden. Der STO-2G-Basissatz wird selten benutzt, da die Qualität der Ergebnisse oft schlecht ist.[2]
STO-3G
Der am weitesten verbreitete Basissatz dieser Gruppe ist STO-3G, der für große Systeme und für qualitative Ergebnisse verwendet wird. Die Koeffizienten und Exponenten für Atome der ersten und der zweiten Periode sind wie folgt gegeben (für ).[3]
| STO-3G | α1 | c1 | α2 | c2 | α3 | c3 |
| 1s | 2.22766 | 0.154329 | 0.405771 | 0.535328 | 0.109818 | 0.444635 |
| 2s | 0.994203 | -0.0999672 | 0.231031 | 0.399515 | 0.0751386 | 0.700115 |
| 2p | 0.994203 | 0.155916 | 0.231031 | 0.607684 | 0.0751386 | 0.391957 |
Höhere STO-NG-Basissätze
Höhere STO-NG-Basissätze werden aufgrund niedriger Flexibilität selten benutzt.[2]
Die genaue Energie des 1s-Elektrons des H-Atoms ist −0,5 Hartree, gegeben durch ein einzelnes Slater-Orbital mit dem Exponenten 1,0. Die folgende Tabelle zeigt die Zunahme der Genauigkeit, wenn die Anzahl primitiver Gaußfunktionen von 3 auf 6 im Basissatz ansteigt:[4]
| Basissatz | Energie [Hartree] |
| STO-3G | −0.49491 |
| STO-4G | −0.49848 |
| STO-5G | −0.49951 |
| STO-6G | −0.49983 |
Anwendungen
STO-NG-Basissätze werden meistens für große Systeme oder für Voruntersuchungen der Geometrie verwendet. Für Ab-initio-Berechnungen von guter Qualität sind die STO-NG-Basissätze allerdings ungeeignet, da ihre Flexibilität in radialer Richtung schlecht ist. Für ausreichend gute Berechnungen sind daher flexiblere Basissätze, wie z. B. Pople-Basen, notwendig.[1]
Einzelnachweise
- ↑ a b c Kunz, Roland W.: Molecular Modelling für Anwender: Anwendung von Kraftfeld- und MO-Methoden in der organischen Chemie. 1. Auflage. Teubner, Stuttgart 1991, ISBN 3-519-03511-1, S. 122.
- ↑ a b c Young, David C.: Computational chemistry : a practical guide for applying techniques to real world problems. Wiley, New York 2001, ISBN 0-471-33368-9, S. 86.
- ↑ a b Trygve Helgaker, Poul Jørgensen, Jeppe Olsen: Molecular Electronic‐Structure Theory. John Wiley & Sons, LTD, Chichester 2000, ISBN 978-0-471-96755-2.
- ↑ a b c W. J. Hehre, R. F. Stewart, J. A. Pople: Self‐Consistent Molecular‐Orbital Methods. I. Use of Gaussian Expansions of Slater‐Type Atomic Orbitals. Band 51. The Journal of Chemical Physics, 1969, S. 2657, doi:10.1063/1.1672392.
- ↑ Alan Hinchliffe: Chemical Modeling From Atoms to Liquids. John Wiley & Sons, Ltd., 1999, S. 294.
- ↑ Andrew R. Leach: Molecular Modelling. Longman, Harlow 1996, S. 68–73.
- ↑ Robert F. Stewart: Small Gaussian Expansions of Slater‐Type Orbitals. In: The Journal of Chemical Physics. 52. Jahrgang, Nr. 1, 1970, S. 431–438, doi:10.1063/1.1672702 (englisch).
- ↑ Benjamin P. Pritchard, Doaa Altarawy, Brett Didier, Tara D. Gibson, Theresa L. Windus: A New Basis Set Exchange: An Open, Up-to-date Resource for the Molecular Sciences Community. In: Journal of Chemical Information and Modeling. 59. Jahrgang, Nr. 11, 2019, S. 4814–4820, doi:10.1021/acs.jcim.9b00725 (englisch, basissetexchange.org).