Rankine-Körper

Der Rankine-Körper – benannt nach dem schottischen Physiker und Ingenieur William John Macquorn Rankine – ist ein in der Ebene liegender, im Bild nach rechts halbunendlich ausgedehnter Körper. Die Breite des Körpers ist beschränkt.^[1][2]

Die im Bild dargestellten Stromlinien und das Druckfeld gehören zu einer ebenen Potentialströmung eines viskositäts­freien inkompressiblen Fluids (Flüssigkeit oder Gas), das den Rankine-Körper umfließt. Der Volumenstrom ist zwischen zwei Stromlinien überall gleich, siehe Stromfunktion, sodass die Geschwindigkeit dort, wo die Linien nahe beieinander liegen höher und andernorts geringer ist.

Vor dem Körper nimmt die Geschwindigkeit ab weil der Druck ansteigt, was das Fluid nach oben und unten ausweichen lässt. Im Zentrum des Gebiets hohen Drucks vor dem Körper (rot im Bild) bildet sich ein Staupunkt, in dem die Strömung zur Ruhe kommt und der Druck um den Staudruck erhöht ist, siehe #Druckfeld und Staupunktströmung. Vor dem Körper durchläuft die Geschwindigkeit ein Minimum und der Druck ein Maximum. Der Körper verdrängt die Strömung nach oben und unten, was neben ihm wie in einer Venturi-Düse zu einer Geschwindigkeits­zunahme führt, die nach dem Bernoulli-Effekt von einer Druckabnahme begleitet wird (dunkler blaue Bereiche). Im weiteren Verlauf nähern sich Druck und Geschwindigkeit wieder den Werten im Fernfeld an, siehe #Druck und Geschwindigkeit auf der Staupunktsstromlinie.

Es ist statthaft, die ebene Potentialströmung senkrecht zur Bildebene zu extrudieren, wodurch die Strömung dreidimensional und der Rankine-Körper brettförmig wird.

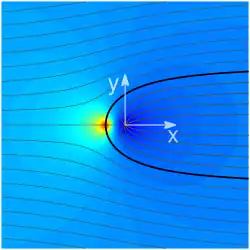
Da die Strömung in der Ebene stattfindet, können die Eigenschaften komplexer Funktionen ausgenutzt werden. Die xy-Ebene wird als Gaußsche Zahlenebene interpretiert und ein komplexes Geschwindigkeitspotential definiert, dessen Imaginärteil die Stromfunktion ist, deren Höhenlinien Stromlinien sind. Die Strömung ist dann automatisch volumenerhaltend und wirbelfrei.

Der Imaginärteil des Geschwindigkeits­potentials ist die Stromfunktion, deren Höhenlinien Stromlinien sind, die in einer stationären Strömung wie hier mit den Bahnlinien übereinstimmen. Es tritt an keiner Stelle der Stromlinie Fluid über sie hinweg: Stromlinien können hier als undurch­dringliche Wände aufgefasst werden.^[3] Dies gilt insbesondere für die Staupunkts­stromlinie, die vor dem Körper auf der x-Achse verläuft und im Staupunkt in die Kontur des Körpers verzweigt, fett schwarz in Abb. 2.

Potentialströmungen können superponiert werden^[4][3] und diese hier entsteht aus der Überlagerung einer Parallel­strömung in der Ebene und einer Quell­strömung im vorderen Teil des Körpers, siehe Abb. 2. Einerseits verdrängt die Quell­strömung die Parallel­strömung nach oben und unten und andererseits begrenzt die Parallel­strömung die Ausbreitung der Quell­strömung in Richtung Luv.

Bei einer Senke (mit negativer Stärke Q) prallen die obere und untere Umströmung des Körpers im Staupunkt aufeinander und stoppen sich dort gegenseitig. Wenn Q und die Strömungs­geschwindigkeit gleiches Vorzeichen besitzen, ergeben sich Stromlinien wie in den Bildern gezeigt, und bei umgekehrten Vorzeichen erscheint das Strömungsbild an der y-Achse gespiegelt. Hier wird eine positive Strömungs­geschwindigkeit in x-Richtung und zunächst eine Quelle mit Q>0 angenommen.

Das Geschwindigkeitspotential einer Parallelströmung mit Geschwindigkeit u_∞∈ℝ in x-Richtung ist Π_∥(z)=u_∞z, und dasjenige einer Quelle mit Quellstärke Q im Ursprung lautet mit dem natürlichen Logarithmus ln: ${\displaystyle {\mathsf {\Pi _{*}(z)={\tfrac {Q}{2\pi }}\ln(z)}}}$. Deren Superposition ist die Summe^[4][3]

${\displaystyle {\mathsf {\Pi (z)=\Pi _{\parallel }(z)+\Pi _{*}(z)=u_{\infty }\,z+{\frac {Q}{2\pi }}\ln(z)}}}$

Eine komplexe Zahl schreibt sich mit der imaginären Einheit j in der Polardarstellung als z=r·e^jφ. Bei gegebenem z ist das Argument φ nur bis auf Vielfache von 2π bestimmt. Einsetzen der Polardarstellung liefert mit einer ganzen Zahl n:

${\displaystyle {\mathsf {\Pi (r,\varphi )=u_{\infty }\,r\,e^{j\,(\varphi +2\,n\,\pi )}+{\frac {Q}{2\pi }}{\big (}\ln(r)+j(\varphi +2\,n\,\pi ){\big )}}}}$

Die Stromfunktion ist der Imaginärteil hiervon:

${\displaystyle {\mathsf {\psi (r,\varphi )=u_{\infty }\,r\,\sin(\varphi +2\,n\,\pi )+{\frac {Q}{2\pi }}(\varphi +2\,n\,\pi )=u_{\infty }\,r\,\sin(\varphi )+{\frac {Q}{2\pi }}(\varphi +2\,n\,\pi )}}}$

Die komplexe Geschwindigkeit w ist die Ableitungsfunktion des Potentials Π(z):

${\displaystyle {\mathsf {w=u-j\,v={\frac {d}{dz}}\Pi (z)=u_{\infty }+{\frac {Q}{2\pi \,z}}=u_{\infty }+{\frac {Q\,{\bar {z}}}{2\pi \,r^{2}}}=u_{\infty }+{\frac {Q\,x}{2\pi \,r^{2}}}-j\,{\frac {Q\,y}{2\pi \,r^{2}}}}}}$

mit der Geschwindigkeit u in x-Richtung und v in y-Richtung, z=x+j·y, wobei der Überstrich die komplexe Konjugation bedeutet, sowie ${\displaystyle {\mathsf {r=|z|={\sqrt {x^{2}+y^{2}}}}}}$. In der Polar­darstellung ergibt sich:

${\displaystyle {\mathsf {w=u_{\infty }+{\frac {Q\,r\,\cos(\varphi )}{2\pi \,r^{2}}}-j\,{\frac {Q\,r\,\sin(\varphi )}{2\pi \,r^{2}}}=u_{\infty }+{\frac {Q\,\cos(\varphi )}{2\pi \,r}}-j\,{\frac {Q\,\sin(\varphi )}{2\pi \,r}}}}}$

Bei Annäherung an das Zentrum der Quelle mit r→0 wächst die Geschwindigkeit über alle Grenzen, was unphysikalisch ist: In der Nähe der Quelle verlieren die Gleichungen der Potential­strömung ihre Gültigkeit. Im Staupunkt auf der x-Achse bei

${\displaystyle {\mathsf {x_{s}=-{\frac {Q}{2\pi \,u_{\infty }}}={\frac {Q}{2\pi \,u_{\infty }}}\,e^{j\pi }}}}$

verschwindet die Geschwindigkeit.

In Potentialströmungen gilt die Bernoulli-Gleichung global, also zwischen zwei beliebigen Punkten in der Strömung. Mit dem Druck p und der Dichte ρ des Fluids (Flüssigkeit oder Gas) lautet die Druckgleichung bei vernach­lässigbarem Schwerefeld:

${\displaystyle {\mathsf {C=p+{\frac {\rho }{2}}|w|^{2}=p+{\frac {\rho }{2}}\left(u^{2}+v^{2}\right)={\text{const.}}}}}$

In einem (unendlich) weit vom Rankine-Körper entfernten Punkt herrscht der Umgebungs- oder Betriebsdruck p₀ und die Strömungs­geschwindigkeit ist u_∞, was die Konstante C festlegt:

${\displaystyle {\mathsf {C=p_{0}+{\frac {\rho }{2}}\,u_{\infty }^{2}}}}$

Im Staupunkt herrscht Stillstand mit w=0:

${\displaystyle {\mathsf {C=p_{s}+{\frac {\rho }{2}}|0|^{2}=p_{s}}}}$

In einem beliebigen Ort ist mit den Geschwindigkeiten aus dem vorhergehenden Abschnitt

${\displaystyle {\mathsf {p+{\frac {\rho }{2}}|w|^{2}=p_{s}\;\rightarrow \;p=p_{0}-{\frac {\rho }{2}}\,{\frac {Q\,(Q+4\,\pi \,u_{\infty }\,x)}{(2\,\pi \,r)^{2}}}}}}$

Im Fernfeld bei r→±∞ herrscht der Umgebungsdruck p₀, und auch diese Gleichung verliert in der Nähe der Quelle ihre Gültigkeit.

Im Staupunkt ist r=|x_s|, φ=π und die Stromfunktion hat den Wert ${\displaystyle {\mathsf {\psi ={\tfrac {Q}{2}}(2n+1),\;n\in \{-1,0\}}}}$, woraus sich die Staupunkts­stromlinie, die gleichzeitig die Kontur des Rankine-Körpers ist, berechnet:

${\displaystyle {\mathsf {\psi ={\frac {Q}{2}}(2n+1)=u_{\infty }\,r\,\sin(\varphi )+{\frac {Q}{2\pi }}(\varphi +2\,n\,\pi )\quad \rightarrow \quad r={\frac {Q(\pi -\varphi )}{2\pi \,u_{\infty }\,\sin(\varphi )}}}}}$

Letztere Identität definiert die Staupunkts­stromlinie, deren Abstand von der x-Achse

${\displaystyle {\mathsf {y=r\,\sin(\varphi )={\frac {Q(\pi -\varphi )}{2\pi \,u_{\infty }}}}}}$

ist. Bei φ→0 und r→∞ strebt die Breite b des Rankine-Körpers zum Maximum

${\displaystyle {\mathsf {y_{\infty }={\frac {Q}{2\,u_{\infty }}}\;\rightarrow \;b:=2\,y_{\infty }={\frac {Q}{u_{\infty }}}}}}$

Diese Breite ergibt sich einfacher aus einer Bilanz, denn der aus der Quelle austretende Volumenstrom Q fließt rechts mit der Geschwindigkeit u_∞ über den Querschnitt b ab, also Q=b·u_∞.^[3]

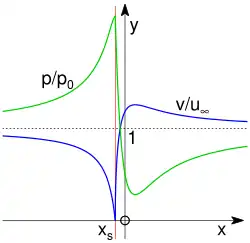
Bei Q>0, was hier angenommen wird, folgt die Staupunkts­stromlinie vor dem Staupunkt der x-Achse und verzweigt im Staupunkt in die Kontur des Rankine-Körpers.

Vor dem Staupunkt ist y=0, r=−x, φ=π und ${\displaystyle {\mathsf {x<-{\tfrac {Q}{2\pi \,u_{\infty }}}}}}$:

${\displaystyle {\begin{aligned}{\mathsf {v}}:=&|w|={\mathsf {u=u_{\infty }+{\frac {Q}{2\pi \,x}}\geq 0}}\\{\mathsf {p}}=&{\mathsf {p_{0}-{\frac {\rho }{2}}\,{\frac {Q\,(Q+4\,\pi \,u_{\infty }\,x)}{(2\,\pi \,x)^{2}}}}}\end{aligned}}}$

Der Druck steigt an und bremst die Strömung bis zum Stillstand im Staupunkt ab. Hinter dem Staupunkt ist

${\displaystyle {\begin{aligned}{\mathsf {v}}=&{\mathsf {u_{\infty }{\sqrt {1+{\frac {{\big (}\sin(\varphi )+2(\pi -\varphi )\cos(\varphi ){\big )}\sin(\varphi )}{(\pi -\varphi )^{2}}}}}}}\\{\mathsf {p}}=&{\mathsf {p_{0}-{\frac {{\big (}\sin(\varphi )+2(\pi -\varphi )\cos(\varphi ){\big )}\sin(\varphi )}{(\pi -\varphi )^{2}}}\,{\frac {\rho }{2}}\,u_{\infty }^{2}}}\end{aligned}}}$

Die Verläufe sind in Abb. 3 dargestellt. Deutlich ist der Stillstand und das Druckmaximum im Staupunkt bei x=x_s abzulesen. Hinter dem Staupunkt tritt ein Geschwindigkeits­maximum auf, in dem der Druck im Minimum ist. Im weiteren Verlauf – in x-Richtung – nähern sich die Geschwindigkeit und der Druck dem Wert im Fernfeld an.

Wenn im Ursprung statt einer Quelle mit Q>0 eine Senke mit Q<0 vorliegt, zeigt sich ein umgekehrter Verlauf in x-Richtung: Die Geschwindigkeit steigt an, um dann zum Staupunkt hin schnell auf null abzufallen, wo die obere und untere Umströmung des Körpers aufeinandertreffen. Der Druck durchläuft entsprechend ein Minimum und steigt zum Staupunkt am Ende des Körpers rasant an. Bei viskosen Fluiden kann dies zu einer Grenzschichtablösung führen.^[3]

Commons: Potentialströmung – Sammlung von Bildern, Videos und Audiodateien

1. ↑ Christian Hauser: Rechenübung Strömungsmechanik 2. (PDF) 322.050. Institut für Strömungsmechanik und Wärmeübertragung an der TU-Wien, 22. November 2013, S. 1, abgerufen am 23. Mai 2025. 
2. ↑ G. L. Korolev, V. V. Sychev: Boundary Layer over the Rankine Half-Body. In: Fluid Dynamics. Band 56, 29. November 2021, ISSN 0015-4628, S. 824–827, doi:10.1134/S0015462821060082. 
3. ↑ ^{a b c d e} J. Zierep, K. Bühler: Grundzüge der Strömungslehre. Grundlagen, Statik und Dynamik der Fluide. 9. Auflage. Springer Vieweg, Wiesbaden 2013, ISBN 978-3-658-01605-0, Beispiele für elementare und zusammengesetzte Potentialströmungen, S. 95–99, doi:10.1007/978-3-658-01606-7. 
4. ↑ ^{a b} A. Huber: Technische Mechanik 4. Hydromechanik. Springer Vieweg, Berlin, Heidelberg 2025, ISBN 978-3-662-69230-1, Zweidimensionale Potentialströmungen, S. 363 f., doi:10.1007/978-3-662-69231-8_6.