Regel der Mittelzahlen

Die Regel der Mittelzahlen (französisch regle des nombres moyens) ist ein mathematischer Lehrsatz der elementaren Algebra und Zahlentheorie. Er formuliert zwei Ungleichungen, mit denen die so genannte Mediante zweier Brüche zu diesen in Beziehung gesetzt wird.^[1][2][3] Der Satz wird dem französischen Mathematiker Nicolas Chuquet zugerechnet, der ihn im Jahre 1484 veröffentlichte.

Sind ${\displaystyle a,b,x,y}$ reelle Zahlen mit ${\displaystyle b,y>0}$^{[A 1]} und ${\displaystyle {\frac {a}{b}}<{\frac {x}{y}}}$, so gelten die Ungleichungen

${\displaystyle {\frac {a}{b}}<{\frac {a+x}{b+y}}<{\frac {x}{y}}}$.

Eine entsprechende Aussage gilt auch, wenn anstelle des Kleinerzeichens das Kleiner-gleich-Zeichen vorliegt.

Man nennt den mittleren Bruch der Ungleichungskette die Mediante^[3] der beiden Ausgangsbrüche ${\displaystyle {\frac {a}{b}}}$ und ${\displaystyle {\frac {x}{y}}}$. Die Regel der Mittelzahlen besagt also, dass die Mediante zweier (verschiedener) Brüche immer zwischen diesen beiden Brüchen liegt. Dies erklärt, warum man die Mediante als Mittelwert ansieht. Aus historischen Gründen wird dieser Mittelwert auch Chuquet-Mittel genannt.^[4]

Für ${\displaystyle a=-2,b=3,x=-1,y=2}$ erhält man

${\displaystyle {\frac {-2}{3}}<{\frac {(-2)+(-1)}{3+2}}<{\frac {-1}{2}}}$.

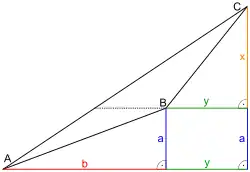
Die Regel der Mittelzahlen bzw. das Chuquet-Mittel lässt sich geometrisch interpretieren, indem man die Brüche als Steigungen von Strecken interpretiert: Die Steigung ${\displaystyle {\frac {a+x}{b+y}}}$ der Strecke ${\displaystyle AC}$ liegt stets zwischen der Steigung ${\displaystyle {\frac {a}{b}}}$ der Strecke ${\displaystyle AB}$ und der Steigung ${\displaystyle {\frac {x}{y}}}$ der Strecke ${\displaystyle BC}$ (Figur 1).^[5][6]

1. ↑ In Eves’ Introduction to the History of Mathematics wird die Positivität der vier Zahlen vorausgesetzt, während im Lexikon bedeutender Mathematiker hierzu keine Voraussetzungen genannt sind. Jedenfalls muss der Fall ${\displaystyle b+y=0}$ ausgeschlossen werden.

• Micolas Chuquet: Triparty en la science des nombres. 1484
• Howard Eves: An Introduction to the History of Mathematics (= The Saunders Series). 5. Auflage. Saunders College Publishing, Philadelphia u. a. 1983, ISBN 0-03-062064-3, S. 214 (MR0684360)
• Siegfried Gottwald, Hans-Joachim Ilgauds, Karl-Heinz Schlote (Hrsg.): Lexikon bedeutender Mathematiker. Verlag Harri Deutsch, Thun 1990, ISBN 3-8171-1164-9, S. 103–104 (MR1089881).

1. ↑ Siegfried Gottwald et al. (Hrsg.): Lexikon bedeutender Mathematiker. 1990, S. 104
2. ↑ Howard Eves: An Introduction to the History of Mathematics. 1983, S. 214
3. ↑ ^{a b} Guido Walz (Hrsg.): Lexikon der Mathematik: Band 3: Inp bis Mon. 2. Auflage. Springer Spektrum, Berlin / Heidelberg 2017, ISBN 978-3-662-53501-1, S. 397. 
4. ↑ Horst Hischer: Grundlegende Begriffe der Mathematik: Entstehung und Entwicklung. 2. Auflage. Springer, Berlin / Heidelberg 2021, ISBN 978-3-662-62232-2, S. 285. 
5. ↑ Roger B. Nelsen: Beweise ohne Worte, Deutschsprachige Ausgabe herausgegeben von Nicola Oswald, Springer Spektrum, Springer-Verlag Berlin Heidelberg 2016, ISBN 978-3-662-50330-0, Seite 143
6. ↑ Richard A. Gibbs: Proof without Words: The Mediant Property. In: Mathematics Magazine. Band 63, Nr. 3, 1990, S. 172, doi:10.1080/0025570X.1990.11977511.