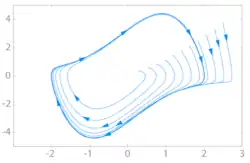
In der Theorie dynamischer Systeme bezeichnet man als Limesmengen (oder Grenzwertmenge ) diejenigen Punkte des Zustandsraums , denen sich Orbits (für positive oder negative Zeit) unendlich oft annähern.
ω
{\displaystyle \omega }
Van-der-Pol-Oszillators
Definition
Sei
(
T
,
X
,
Φ
)
{\displaystyle (T,X,\Phi )}
T
=
Z
{\displaystyle T=\mathbb {Z} }
T
=
R
{\displaystyle T=\mathbb {R} }
x
∈
X
{\displaystyle x\in X}
Die
ω
{\displaystyle \omega }
x
{\displaystyle x}
ω
(
x
,
Φ
)
:=
{
y
∈
X
:
∃
t
n
→
∞
,
Φ
(
t
n
,
x
)
→
y
}
{\displaystyle \omega (x,\Phi ):=\left\{y\in X:\exists t_{n}\rightarrow \infty ,\Phi (t_{n},x)\rightarrow y\right\}}
Die
α
{\displaystyle \alpha }
x
{\displaystyle x}
α
(
x
,
Φ
)
:=
{
y
∈
X
:
∃
t
n
→
−
∞
,
Φ
(
t
n
,
x
)
→
y
}
{\displaystyle \alpha (x,\Phi ):=\left\{y\in X:\exists t_{n}\rightarrow -\infty ,\Phi (t_{n},x)\rightarrow y\right\}}
Alternativ lassen sich Limesmengen auch wie folgt charakterisieren:
ω
(
x
,
Φ
)
=
⋂
n
∈
T
{
Φ
(
t
,
x
)
:
t
>
n
}
¯
{\displaystyle \omega (x,\Phi )=\bigcap _{n\in T}{\overline {\left\{\Phi (t,x):t>n\right\}}}}
α
(
x
,
Φ
)
=
⋂
n
∈
T
{
Φ
(
t
,
x
)
:
t
<
n
}
¯
{\displaystyle \alpha (x,\Phi )=\bigcap _{n\in T}{\overline {\left\{\Phi (t,x):t<n\right\}}}}
Die Limesmengen sind abgeschlossen und invariant unter
Φ
{\displaystyle \Phi }
X
{\displaystyle X}
Typen
Literatur
Gerald Teschl : Ordinary Differential Equations and Dynamical Systems (= Graduate Studies in Mathematics . Band 140 ). American Mathematical Society, Providence 2012, ISBN 978-0-8218-8328-0 (mat.univie.ac.at ).