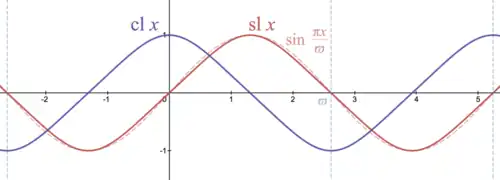
Lemniskatischer Sinus (rot) und lemniskatischer Kosinus (blau) für ein reelles Argument, im Vergleich mit der trigonometrischen Sinusfunktion
y
=
sin
(
π
x
/
ϖ
)
{\displaystyle y=\sin(\pi x/\varpi )}
Die Länge s des Lemniskatenbogens vom Ursprung korreliert mit dem Abstand r des Kurvenpunktes zum Ursprung.Quadrant enthält einen Viertelbogen (der Länge
ϖ
2
{\displaystyle {\tfrac {\varpi }{2}}}
Brennpunkte liegen hier bei
(
±
1
2
∣
0
)
{\displaystyle \left(\pm {\tfrac {1}{\sqrt {2}}}\mid 0\right)}
Der lemniskatische Sinus (lateinisch Sinus lemniscatus ) und der lemniskatische Kosinus (lateinisch Cosinus lemniscatus ), abgekürzt mit
sinlemn
{\displaystyle \operatorname {sinlemn} }
coslemn
{\displaystyle \operatorname {coslemn} }
sl
{\displaystyle \operatorname {sl} }
cl
{\displaystyle \operatorname {cl} }
Carl Friedrich Gauß eingeführte mathematische Funktionen . Sie haben für die Lemniskate von Bernoulli die entsprechende Bedeutung wie die Sinus- und die Kosinusfunktion für den Kreis.
Die Funktionen
sl
{\displaystyle \operatorname {sl} }
cl
{\displaystyle \operatorname {cl} }
meromorphen Funktionen in
C
{\displaystyle \mathbb {C} }
komplexen Zahlen ) fortsetzen. Sie erfüllen die Periodizitätseigenschaften
sl
(
z
+
2
ϖ
)
=
sl
(
z
)
,
sl
(
z
+
2
i
ϖ
)
=
sl
(
z
)
,
cl
(
z
+
2
ϖ
)
=
cl
(
z
)
,
cl
(
z
+
2
i
ϖ
)
=
cl
(
z
)
,
{\displaystyle {\begin{aligned}\operatorname {sl} (z+2\varpi )=\operatorname {sl} (z),\qquad &\operatorname {sl} (z+2\mathrm {i} \varpi )=\operatorname {sl} (z),\\\operatorname {cl} (z+2\varpi )=\operatorname {cl} (z),\qquad &\operatorname {cl} (z+2\mathrm {i} \varpi )=\operatorname {cl} (z),\end{aligned}}}
wobei
ϖ
=
2,622
05
…
{\displaystyle \varpi =2{,}62205\ldots }
lemniskatische Konstante ist, und gehören daher (als historisch erste Beispiele) zu den elliptischen Funktionen .
Der lemniskatische Kosinus kann direkt vom lemniskatischen Sinus abgeleitet werden. Verschiebt man nämlich den Graphen der Funktion
sl
{\displaystyle \operatorname {sl} }
ϖ
2
{\displaystyle {\tfrac {\varpi }{2}}}
cl
{\displaystyle \operatorname {cl} }
Geschichte
Der 19-jährige Gauß beschäftigte sich 1796 (in erst nach seinem Tod veröffentlichten Notizen) mit der Frage, wie man aus einer gegebenen Bogenlänge
s
{\displaystyle s}
r
∈
(
−
1
,
1
)
{\displaystyle r\in (-1,1)}
r
=
0
{\displaystyle r=0}
Umkehrfunktion
r
=
r
(
s
)
{\displaystyle r=r(s)}
elliptischen Integrals
s
(
r
)
=
∫
0
r
d
ρ
1
−
ρ
4
.
{\displaystyle s(r)=\int _{0}^{r}{\frac {\mathrm {d} \,\rho }{\sqrt {1-\rho ^{4}}}}.}
Beweis:
Für den ersten und dritten Quadranten kann die Lemniskate von Bernoulli auf folgende Weise parametrisiert werden:
x und y als Koordinaten eines Punktes auf der Kurve im Abstand r vom Ursprung (Pythagoras) erfüllen die Lemniskatengleichung. Aus diesen zwei Gleichungen ergeben sich
x
(
r
)
=
r
1
+
r
2
/
2
{\displaystyle x(r)=r{\sqrt {1+r^{2}}}/{\sqrt {2}}}
y
(
r
)
=
r
1
−
r
2
/
2
{\displaystyle y(r)=r{\sqrt {1-r^{2}}}/{\sqrt {2}}}
Für die Berechnung der vom Ursprung ausgehenden Kurvenlänge s wird der Pythagoras der ersten Ableitungen von x und y gebildet und dieser integriert:
s
(
r
)
=
∫
0
r
[
d
d
r
x
(
r
)
(
r
=
ρ
)
]
2
+
[
d
d
r
y
(
r
)
(
r
=
ρ
)
]
2
d
ρ
=
{\displaystyle s(r)=\int _{0}^{r}{\sqrt {\left[{\frac {\mathrm {d} }{\mathrm {d} r}}x(r)(r=\rho )\right]^{2}+\left[{\frac {\mathrm {d} }{\mathrm {d} r}}y(r)(r=\rho )\right]^{2}}}\mathrm {d} \rho =}
=
∫
0
r
[
d
d
ρ
ρ
1
+
ρ
2
/
2
]
2
+
[
d
d
ρ
ρ
1
−
ρ
2
/
2
]
2
d
ρ
=
{\displaystyle =\int _{0}^{r}{\sqrt {\left[{\frac {\mathrm {d} }{\mathrm {d} \rho }}\rho {\sqrt {1+\rho ^{2}}}/{\sqrt {2}}\right]^{2}+\left[{\frac {\mathrm {d} }{\mathrm {d} \rho }}\rho {\sqrt {1-\rho ^{2}}}/{\sqrt {2}}\right]^{2}}}\mathrm {d} \rho =}
=
∫
0
r
(
1
+
2
ρ
2
)
2
2
(
1
+
ρ
2
)
+
(
1
−
2
ρ
2
)
2
2
(
1
−
ρ
2
)
d
ρ
=
∫
0
r
1
1
−
ρ
4
d
ρ
{\displaystyle =\int _{0}^{r}{\sqrt {{\frac {(1+2\rho ^{2})^{2}}{2(1+\rho ^{2})}}+{\frac {(1-2\rho ^{2})^{2}}{2(1-\rho ^{2})}}}}\mathrm {d} \rho =\int _{0}^{r}{\frac {1}{\sqrt {1-\rho ^{4}}}}\mathrm {d} \rho }
Gauß nannte diese Umkehrfunktion Sinus lemniscatus und bezeichnete sie mit
sl
{\displaystyle \operatorname {sl} }
r
=
sl
s
{\displaystyle r=\operatorname {sl} \,s}
Entsprechend definierte er den Cosinus lemniscatus
cl
s
=
sl
(
ϖ
2
−
s
)
{\displaystyle \operatorname {cl} \,s=\operatorname {sl} \,({\tfrac {\varpi }{2}}-s)}
ϖ
{\displaystyle \varpi }
ϖ
=
2
∫
0
1
d
ρ
1
−
ρ
4
≈
2,622
05
75542
92119
81046
48395
89891
…
{\displaystyle \varpi =2\int _{0}^{1}{\frac {\mathrm {d} \,\rho }{\sqrt {1-\rho ^{4}}}}\approx 2{,}62205\ 75542\ 92119\ 81046\,48395\ 89891\ldots }
A062539 in OEIS )Gauß ließ sich bei diesen Bezeichnungen von der Analogie zu den Kreisfunktionen leiten, denn der Sinus ist die Umkehrfunktion des Integrals
s
(
r
)
=
∫
0
r
d
ρ
1
−
ρ
2
,
und
2
∫
0
1
d
ρ
1
−
ρ
2
=
π
.
{\displaystyle s(r)=\int _{0}^{r}{\frac {\mathrm {d} \,\rho }{\sqrt {1-\rho ^{2}}}},\qquad {\mbox{und}}\qquad 2\int _{0}^{1}{\frac {\mathrm {d} \,\rho }{\sqrt {1-\rho ^{2}}}}=\pi .}
also
r
=
sin
s
{\displaystyle r=\sin s}
cos
s
=
sin
(
π
2
−
s
)
{\displaystyle \cos s=\sin({\tfrac {\pi }{2}}-s)}
sl
{\displaystyle \operatorname {sl} }
cl
{\displaystyle \operatorname {cl} }
Komplexe fortzusetzen. Er bewies dann die Periodizitätsrelationen
sl
(
s
+
2
ϖ
)
=
sl
s
,
sl
(
s
+
2
i
ϖ
)
=
sl
s
.
{\displaystyle \operatorname {sl} \,(s+2\varpi )=\operatorname {sl} \,s,\qquad \operatorname {sl} \,(s+2\mathrm {i} \varpi )=\operatorname {sl} \,s.}
Im Gegensatz zum Sinus hat also der lemniskatische Sinus
sl
{\displaystyle \operatorname {sl} }
zwei Perioden
2
ϖ
{\displaystyle 2\varpi }
2
i
ϖ
{\displaystyle 2\mathrm {i} \varpi }
cl
{\displaystyle \operatorname {cl} }
elliptisch . Carl Gustav Jacobi führte um 1830 die jacobischen elliptischen Funktionen ein und verallgemeinerte damit die beiden lemniskatischen Funktionen. Diese lassen sich auf folgende Weise durch die Jacobi-Funktionen mit dem Modul λ*(1) = 1/sqrt(2) ausdrücken:
sl
(
s
)
=
sd
(
2
s
;
1
/
2
)
/
2
{\displaystyle \operatorname {sl} \,(s)=\operatorname {sd} ({\sqrt {2}}s;1/{\sqrt {2}})/{\sqrt {2}}}
cl
(
s
)
=
cn
(
2
s
;
1
/
2
)
{\displaystyle \operatorname {cl} \,(s)=\operatorname {cn} ({\sqrt {2}}s;1/{\sqrt {2}})}
Somit sind der lemniskatische Sinus und der lemniskatische Cosinus auch über die Thetafunktionen auf folgende Weise[ 1]
sl
(
s
)
=
ϑ
10
(
π
/
2
−
π
s
/
ϖ
;
e
−
π
)
ϑ
01
(
π
/
2
−
π
s
/
ϖ
;
e
−
π
)
{\displaystyle \operatorname {sl} \,(s)={\frac {\vartheta _{10}(\pi /2-\pi s/\varpi ;\operatorname {e} ^{-\pi })}{\vartheta _{01}(\pi /2-\pi s/\varpi ;\operatorname {e} ^{-\pi })}}}
cl
(
s
)
=
ϑ
10
(
π
s
/
ϖ
;
e
−
π
)
ϑ
01
(
π
s
/
ϖ
;
e
−
π
)
{\displaystyle \operatorname {cl} \,(s)={\frac {\vartheta _{10}(\pi s/\varpi ;\operatorname {e} ^{-\pi })}{\vartheta _{01}(\pi s/\varpi ;\operatorname {e} ^{-\pi })}}}
Definitionen
Die lemniskatischen Funktionen
sl
{\displaystyle \operatorname {sl} }
cl
{\displaystyle \operatorname {cl} }
Anfangswertproblems
d
d
z
sl
z
=
(
1
+
sl
2
z
)
cl
z
,
d
d
z
cl
z
=
−
(
1
+
cl
2
z
)
sl
z
,
sl
0
=
0
,
cl
0
=
1.
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} z}}\operatorname {sl} z={\bigl (}1+\operatorname {sl} ^{2}z{\bigr )}\operatorname {cl} z,\ {\frac {\mathrm {d} }{\mathrm {d} z}}\operatorname {cl} z=-{\bigl (}1+\operatorname {cl} ^{2}z{\bigr )}\operatorname {sl} z,\ \operatorname {sl} 0=0,\ \operatorname {cl} 0=1.}
Äquivalent dazu ist die Definition als Umkehrfunktion zu einem elliptischen Integral :
z
=
∫
0
sl
z
d
t
1
−
t
4
=
∫
cl
z
1
d
t
1
−
t
4
.
{\displaystyle z=\int _{0}^{\operatorname {sl} z}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}}=\int _{\operatorname {cl} z}^{1}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}}.}
Eine weitere Möglichkeit ist die Definition als Schwarz-Christoffel-Transformation von der Einheitskreisscheibe der komplexen Zahlenebene auf das Quadrat mit den Ecken
1
2
ϖ
,
1
2
ϖ
i
,
−
1
2
ϖ
,
−
1
2
ϖ
i
{\displaystyle {\tfrac {1}{2}}\varpi ,{\tfrac {1}{2}}\varpi \mathrm {i} ,-{\tfrac {1}{2}}\varpi ,-{\tfrac {1}{2}}\varpi \mathrm {i} }
[ 2] analytische Fortsetzung bzw. wiederholte Spiegelungen auf die gesamte Zahlenebene fortgesetzt werden.
Zum Vergleich die entsprechenden Definitionsmöglichkeiten für die Sinus- und die Kosinusfunktion:
d
d
z
sin
z
=
cos
z
,
d
d
z
cos
z
=
−
sin
z
,
sin
0
=
0
,
cos
0
=
1
,
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} z}}\sin z=\cos z,\ {\frac {\mathrm {d} }{\mathrm {d} z}}\cos z=-\sin z,\ \sin 0=0,\ \cos 0=1,}
z
=
∫
0
sin
z
d
t
1
−
t
2
=
∫
cos
z
1
d
t
1
−
t
2
.
{\displaystyle z=\int _{0}^{\sin z}{\frac {\mathrm {d} t}{\sqrt {1-t^{2}}}}=\int _{\cos z}^{1}{\frac {\mathrm {d} t}{\sqrt {1-t^{2}}}}.}
Schwarz-Christoffel-Transformation der oberen Halbebene auf den Streifen mit Realteil zwischen
−
1
2
π
{\displaystyle -{\tfrac {1}{2}}\pi }
1
2
π
{\displaystyle {\tfrac {1}{2}}\pi }
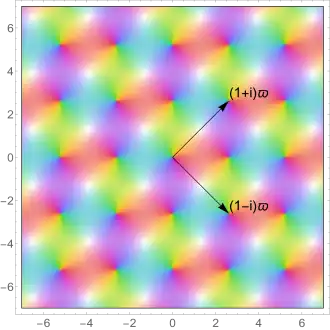
Nullstellen, Pole und Symmetrieeigenschaften
sl
{\displaystyle \operatorname {sl} }
[ 3]
(
1
+
i
)
ϖ
{\displaystyle (1+\mathrm {i} )\varpi }
(
1
−
i
)
ϖ
{\displaystyle (1-\mathrm {i} )\varpi }
Die lemniskatische Funktion
cl
{\displaystyle \operatorname {cl} }
gerade Funktion , dagegen ist
sl
{\displaystyle \operatorname {sl} }
cl
(
−
z
)
=
cl
z
sl
(
−
z
)
=
−
sl
z
{\displaystyle {\begin{aligned}\operatorname {cl} (-z)&=\operatorname {cl} z\\\operatorname {sl} (-z)&=-\operatorname {sl} z\end{aligned}}}
Bei einer Translation um
1
2
ϖ
{\displaystyle {\tfrac {1}{2}}\varpi }
cl
{\displaystyle \operatorname {cl} }
sl
{\displaystyle \operatorname {sl} }
1
2
i
ϖ
{\displaystyle {\tfrac {1}{2}}\mathrm {i} \varpi }
Rotation um
90
∘
{\displaystyle 90^{\circ }}
Kehrwert .
cl
(
z
±
1
2
ϖ
)
=
∓
sl
z
,
cl
(
z
±
1
2
i
ϖ
)
=
∓
i
sl
z
sl
(
z
±
1
2
ϖ
)
=
±
cl
z
,
sl
(
z
±
1
2
i
ϖ
)
=
±
i
cl
z
{\displaystyle {\begin{aligned}{\operatorname {cl} }\left(z\pm {\tfrac {1}{2}}\varpi \right)&=\mp \operatorname {sl} z,&{\operatorname {cl} }\left(z\pm {\tfrac {1}{2}}\mathrm {i} \varpi \right)&={\frac {\mp \mathrm {i} }{\operatorname {sl} z}}\\{\operatorname {sl} }\left(z\pm {\tfrac {1}{2}}\varpi \right)&=\pm \operatorname {cl} z,&{\operatorname {sl} }\left(z\pm {\tfrac {1}{2}}\mathrm {i} \varpi \right)&={\frac {\pm \mathrm {i} }{\operatorname {cl} z}}\end{aligned}}}
Durch zweifache Anwendung einer solchen Translation, also durch eine Translation um
±
ϖ
{\displaystyle \pm \varpi }
±
i
ϖ
{\displaystyle \pm \mathrm {i} \varpi }
Involutionen .
cl
(
z
+
ϖ
)
=
cl
(
z
+
i
ϖ
)
=
−
cl
z
sl
(
z
+
ϖ
)
=
sl
(
z
+
i
ϖ
)
=
−
sl
z
{\displaystyle {\begin{aligned}\operatorname {cl} (z+\varpi )&=\operatorname {cl} (z+\mathrm {i} \varpi )=-\operatorname {cl} z\\\operatorname {sl} (z+\varpi )&=\operatorname {sl} (z+\mathrm {i} \varpi )=-\operatorname {sl} z\end{aligned}}}
Insgesamt sind die beiden Funktionen invariant unter einer Translation um das Produkt einer geraden gaußschen Zahl mit
ϖ
{\displaystyle \varpi }
(
a
+
b
i
)
ϖ
{\displaystyle (a+b\mathrm {i} )\varpi }
a
+
b
=
2
k
{\displaystyle a+b=2k}
a
{\displaystyle a}
b
{\displaystyle b}
k
{\displaystyle k}
cl
(
z
+
(
1
+
i
)
ϖ
)
=
cl
(
z
+
(
1
−
i
)
ϖ
)
=
cl
z
sl
(
z
+
(
1
+
i
)
ϖ
)
=
sl
(
z
+
(
1
−
i
)
ϖ
)
=
sl
z
{\displaystyle {\begin{aligned}{\operatorname {cl} }\left(z+(1+\mathrm {i} )\varpi \right)&={\operatorname {cl} }\left(z+(1-\mathrm {i} )\varpi \right)=\operatorname {cl} z\\{\operatorname {sl} }\left(z+(1+\mathrm {i} )\varpi \right)&={\operatorname {sl} }\left(z+(1-\mathrm {i} )\varpi \right)=\operatorname {sl} z\end{aligned}}}
Dies macht die beiden Funktionen zu elliptischen Funktionen (doppelt periodisch und meromorph in der komplexen Zahlenebene ) mit einem diagonal quadratischen Periodengitter, dessen Perioden
(
1
+
i
)
ϖ
{\displaystyle (1+\mathrm {i} )\varpi }
(
1
−
i
)
ϖ
{\displaystyle (1-\mathrm {i} )\varpi }
Für Spiegelungen und Vierteldrehungen der Argumente einer lemniskatischen Funktion gibt es einfache Rechenausdrücke:
cl
z
¯
=
cl
z
¯
sl
z
¯
=
sl
z
¯
cl
(
i
z
)
=
1
cl
z
sl
(
i
z
)
=
i
sl
z
{\displaystyle {\begin{aligned}\operatorname {cl} {\bar {z}}&={\overline {\operatorname {cl} z}}\\\operatorname {sl} {\bar {z}}&={\overline {\operatorname {sl} z}}\\\operatorname {cl} \left(\mathrm {i} z\right)&={\frac {1}{\operatorname {cl} z}}\\\operatorname {sl} \left(\mathrm {i} z\right)&=\mathrm {i} \operatorname {sl} z\end{aligned}}}
Die Funktion
sl
{\displaystyle \operatorname {sl} }
Nullstellen bei den Produkten von gaußschen Zahlen mit
ϖ
{\displaystyle \varpi }
a
ϖ
+
b
ϖ
i
{\displaystyle a\varpi +b\varpi \mathrm {i} }
a
{\displaystyle a}
b
{\displaystyle b}
Pole bei komplexen Zahlen der Form
(
a
+
1
2
)
ϖ
+
(
b
+
1
2
)
ϖ
i
{\displaystyle \left(a+{\tfrac {1}{2}}\right)\varpi +\left(b+{\tfrac {1}{2}}\right)\varpi \mathrm {i} }
Residuen sind
(
−
1
)
a
−
b
+
1
i
{\displaystyle (-1)^{a-b+1}\mathrm {i} }
cl
{\displaystyle \operatorname {cl} }
sl
{\displaystyle \operatorname {sl} }
cl
z
=
sl
(
1
2
ϖ
−
z
)
{\displaystyle \operatorname {cl} z={\operatorname {sl} }\left({\tfrac {1}{2}}\varpi -z\right)}
cl
{\displaystyle \operatorname {cl} }
(
a
+
1
2
)
ϖ
+
b
ϖ
i
{\displaystyle \left(a+{\tfrac {1}{2}}\right)\varpi +b\varpi \mathrm {i} }
a
ϖ
+
(
b
+
1
2
)
ϖ
i
,
{\displaystyle a\varpi +\left(b+{\tfrac {1}{2}}\right)\varpi \mathrm {i} ,}
(
−
1
)
a
−
b
i
.
{\displaystyle (-1)^{a-b}\mathrm {i} .}
Die Aussage
sl
z
=
sl
w
{\displaystyle \operatorname {sl} z=\operatorname {sl} w}
z
=
(
−
1
)
m
+
n
w
+
(
m
+
n
i
)
ϖ
{\displaystyle z=(-1)^{m+n}w+(m+n\mathrm {i} )\varpi }
m
,
n
∈
Z
{\displaystyle m,n\in \mathbb {Z} }
Algebraische Beziehungen
Folgende algebraische Beziehung gilt für die lemniskatischen Funktionen:
[
1
+
sl
(
x
)
2
]
⋅
[
1
+
cl
(
x
)
2
]
=
2
{\displaystyle [1+\operatorname {sl} (x)^{2}]\cdot [1+\operatorname {cl} (x)^{2}]=2}
Die Additionstheoreme für die lemniskatischen Funktionen lauten wie folgt:
sl
(
a
+
b
)
=
sl
(
a
)
⋅
cl
(
b
)
+
cl
(
a
)
⋅
sl
(
b
)
1
−
sl
(
a
)
⋅
cl
(
a
)
⋅
sl
(
b
)
⋅
cl
(
b
)
{\displaystyle \operatorname {sl} (a+b)={\frac {\operatorname {sl} (a)\cdot \operatorname {cl} (b)+\operatorname {cl} (a)\cdot \operatorname {sl} (b)}{1-\operatorname {sl} (a)\cdot \operatorname {cl} (a)\cdot \operatorname {sl} (b)\cdot \operatorname {cl} (b)}}}
cl
(
a
+
b
)
=
cl
(
a
)
⋅
cl
(
b
)
−
sl
(
a
)
⋅
sl
(
b
)
1
+
sl
(
a
)
⋅
cl
(
a
)
⋅
sl
(
b
)
⋅
cl
(
b
)
{\displaystyle \operatorname {cl} (a+b)={\frac {\operatorname {cl} (a)\cdot \operatorname {cl} (b)-\operatorname {sl} (a)\cdot \operatorname {sl} (b)}{1+\operatorname {sl} (a)\cdot \operatorname {cl} (a)\cdot \operatorname {sl} (b)\cdot \operatorname {cl} (b)}}}
Alternative Darstellungen für die Additionstheoreme:
sl
(
a
+
b
)
=
sl
(
a
)
⋅
sl
′
(
b
)
+
sl
′
(
a
)
⋅
sl
(
b
)
1
+
sl
(
a
)
2
⋅
sl
(
b
)
2
{\displaystyle \operatorname {sl} (a+b)={\frac {\operatorname {sl} (a)\cdot \operatorname {sl} '(b)+\operatorname {sl} '(a)\cdot \operatorname {sl} (b)}{1+\operatorname {sl} (a)^{2}\cdot \operatorname {sl} (b)^{2}}}}
cl
(
a
+
b
)
=
sl
′
(
a
)
⋅
sl
′
(
b
)
−
2
⋅
sl
(
a
)
⋅
sl
(
b
)
1
+
sl
(
a
)
2
+
sl
(
b
)
2
−
sl
(
a
)
2
⋅
sl
(
b
)
2
{\displaystyle \operatorname {cl} (a+b)={\frac {\operatorname {sl} '(a)\cdot \operatorname {sl} '(b)-2\cdot \operatorname {sl} (a)\cdot \operatorname {sl} (b)}{1+\operatorname {sl} (a)^{2}+\operatorname {sl} (b)^{2}-\operatorname {sl} (a)^{2}\cdot \operatorname {sl} (b)^{2}}}}
Dabei ist die Ableitungsfunktion
sl
′
{\displaystyle \operatorname {sl} '}
sl
′
(
x
)
=
cl
(
x
)
⋅
(
1
+
(
sl
(
x
)
)
2
)
{\displaystyle \operatorname {sl} '(x)=\operatorname {cl} (x)\cdot \left(1+(\operatorname {sl} (x))^{2}\right)}
Darstellung über den Arkustangens:
arctan
[
sl
(
a
+
b
)
]
=
arctan
[
sl
(
a
)
⋅
cl
(
b
)
]
+
arctan
[
cl
(
a
)
⋅
sl
(
b
)
]
{\displaystyle \arctan[\operatorname {sl} (a+b)]=\arctan[\operatorname {sl} (a)\cdot \operatorname {cl} (b)]+\arctan[\operatorname {cl} (a)\cdot \operatorname {sl} (b)]}
arctan
[
cl
(
a
+
b
)
]
=
arctan
[
cl
(
a
)
⋅
cl
(
b
)
]
−
arctan
[
sl
(
a
)
⋅
sl
(
b
)
]
{\displaystyle \arctan[\operatorname {cl} (a+b)]=\arctan[\operatorname {cl} (a)\cdot \operatorname {cl} (b)]-\arctan[\operatorname {sl} (a)\cdot \operatorname {sl} (b)]}
Für die Verdopplung gelten diese Formeln:
sl
(
2
x
)
=
2
sl
(
x
)
cl
(
x
)
1
+
sl
(
x
)
2
1
+
sl
(
x
)
4
{\displaystyle \operatorname {sl} (2x)=2\,\operatorname {sl} (x)\operatorname {cl} (x){\frac {1+\operatorname {sl} (x)^{2}}{1+\operatorname {sl} (x)^{4}}}}
cl
(
2
x
)
=
−
1
+
2
cl
(
x
)
2
+
cl
(
x
)
4
1
+
2
cl
(
x
)
2
−
cl
(
x
)
4
{\displaystyle \operatorname {cl} (2x)={\frac {-1+2\,\operatorname {cl} (x)^{2}+\operatorname {cl} (x)^{4}}{1+2\,\operatorname {cl} (x)^{2}-\operatorname {cl} (x)^{4}}}}
Dementsprechend gelten folgende Formeln für die Halbierung:
sl
(
x
2
)
2
=
1
−
cl
(
x
)
1
+
sl
(
x
)
2
1
+
sl
(
x
)
2
+
1
{\displaystyle \operatorname {sl} \left({\frac {x}{2}}\right)^{2}={\frac {1-\operatorname {cl} (x){\sqrt {1+\operatorname {sl} (x)^{2}}}}{{\sqrt {1+\operatorname {sl} (x)^{2}}}+1}}}
cl
(
x
2
)
2
=
1
+
cl
(
x
)
1
+
sl
(
x
)
2
1
+
sl
(
x
)
2
+
1
{\displaystyle \operatorname {cl} \left({\frac {x}{2}}\right)^{2}={\frac {1+\operatorname {cl} (x){\sqrt {1+\operatorname {sl} (x)^{2}}}}{{\sqrt {1+\operatorname {sl} (x)^{2}}}+1}}}
Für die Verdreifachung gilt Folgendes:
sl
(
3
x
)
=
3
sl
(
x
)
−
6
sl
(
x
)
5
−
sl
(
x
)
9
1
+
6
sl
(
x
)
4
−
3
sl
(
x
)
8
{\displaystyle \operatorname {sl} (3x)={\frac {3\,\operatorname {sl} (x)-6\,\operatorname {sl} (x)^{5}-\operatorname {sl} (x)^{9}}{1+6\,\operatorname {sl} (x)^{4}-3\,\operatorname {sl} (x)^{8}}}}
Diese alternativen Darstellungen ermöglichen eine Umkehrung durch Lösen kubischer Gleichungen:
sl
(
3
x
)
=
27
4
(
3
+
1
)
y
−
2
y
3
2
+
27
4
(
3
+
1
)
y
2
[
y
=
3
4
(
3
−
1
)
sl
(
x
)
+
2
sl
(
x
)
3
2
−
3
4
(
3
−
1
)
sl
(
x
)
2
]
{\displaystyle \operatorname {sl} (3x)={\frac {{\sqrt[{4}]{27}}({\sqrt {3}}+1)y-{\sqrt {2}}y^{3}}{{\sqrt {2}}+{\sqrt[{4}]{27}}({\sqrt {3}}+1)y^{2}}}\left[y={\frac {{\sqrt[{4}]{3}}({\sqrt {3}}-1)\operatorname {sl} (x)+{\sqrt {2}}\operatorname {sl} (x)^{3}}{{\sqrt {2}}-{\sqrt[{4}]{3}}({\sqrt {3}}-1)\operatorname {sl} (x)^{2}}}\right]}
sl
(
3
x
)
=
27
4
(
3
+
1
)
z
+
2
z
3
2
−
27
4
(
3
+
1
)
z
2
[
z
=
3
4
(
3
−
1
)
sl
(
x
)
−
2
sl
(
x
)
3
2
+
3
4
(
3
−
1
)
sl
(
x
)
2
]
{\displaystyle \operatorname {sl} (3x)={\frac {{\sqrt[{4}]{27}}({\sqrt {3}}+1)z+{\sqrt {2}}z^{3}}{{\sqrt {2}}-{\sqrt[{4}]{27}}({\sqrt {3}}+1)z^{2}}}\left[z={\frac {{\sqrt[{4}]{3}}({\sqrt {3}}-1)\operatorname {sl} (x)-{\sqrt {2}}\operatorname {sl} (x)^{3}}{{\sqrt {2}}+{\sqrt[{4}]{3}}({\sqrt {3}}-1)\operatorname {sl} (x)^{2}}}\right]}
Der Cosinus Lemniscatus ergibt sich als negatives Analogon zum Sinus Lemniscatus:
cl
(
3
x
)
=
−
3
cl
(
x
)
+
6
cl
(
x
)
5
+
cl
(
x
)
9
1
+
6
cl
(
x
)
4
−
3
cl
(
x
)
8
{\displaystyle \operatorname {cl} (3x)={\frac {-3\,\operatorname {cl} (x)+6\,\operatorname {cl} (x)^{5}+\operatorname {cl} (x)^{9}}{1+6\,\operatorname {cl} (x)^{4}-3\,\operatorname {cl} (x)^{8}}}}
Ableitungen
Die lemniskatischen Funktionen haben folgende Ableitungen:
d
d
x
sl
(
x
)
=
cl
(
x
)
⋅
[
1
+
sl
(
x
)
2
]
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\operatorname {sl} (x)=\operatorname {cl} (x)\cdot [1+\operatorname {sl} (x)^{2}]}
d
d
x
cl
(
x
)
=
−
sl
(
x
)
⋅
[
1
+
cl
(
x
)
2
]
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\operatorname {cl} (x)=-\operatorname {sl} (x)\cdot [1+\operatorname {cl} (x)^{2}]}
Daraus folgt die Tatsache, dass die zweite Ableitung das negative doppelte vom Kubus ist.
d
d
x
d
d
x
sl
(
x
)
=
−
2
⋅
sl
(
x
)
3
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}{\frac {\mathrm {d} }{\mathrm {d} x}}\operatorname {sl} (x)=-2\cdot \operatorname {sl} (x)^{3}}
d
d
x
d
d
x
cl
(
x
)
=
−
2
⋅
cl
(
x
)
3
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}{\frac {\mathrm {d} }{\mathrm {d} x}}\operatorname {cl} (x)=-2\cdot \operatorname {cl} (x)^{3}}
Über die Formeln der Ableitungen lassen sich ebenso die Stammfunktionen von Sinus Lemniscatus und Cosinus lemniscatus ermitteln.
cl
(
x
)
=
d
d
x
arctan
[
sl
(
x
)
]
{\displaystyle \operatorname {cl} (x)={\frac {\mathrm {d} }{\mathrm {d} x}}\arctan[\operatorname {sl} (x)]}
sl
(
x
)
=
−
d
d
x
arctan
[
cl
(
x
)
]
{\displaystyle \operatorname {sl} (x)=-{\frac {\mathrm {d} }{\mathrm {d} x}}\arctan[\operatorname {cl} (x)]}
Spezielle Werte
Einzelne Funktionswerte für die lemniskatischen Funktionen:
sl
(
0
)
=
0
=
cl
(
ϖ
2
)
{\displaystyle \operatorname {sl} \left(0\right)=0=\operatorname {cl} \left({\frac {\varpi }{2}}\right)}
sl
(
ϖ
2
)
=
1
=
cl
(
0
)
{\displaystyle \operatorname {sl} \left({\frac {\varpi }{2}}\right)=1=\operatorname {cl} \left(0\right)}
sl
(
ϖ
4
)
=
2
−
1
=
cl
(
ϖ
4
)
{\displaystyle \operatorname {sl} \left({\frac {\varpi }{4}}\right)={\sqrt {{\sqrt {2}}-1}}=\operatorname {cl} \left({\frac {\varpi }{4}}\right)}
sl
(
ϖ
6
)
=
1
2
⋅
(
3
+
1
−
12
4
)
=
cl
(
ϖ
3
)
{\displaystyle \operatorname {sl} \left({\frac {\varpi }{6}}\right)={\frac {1}{2}}\cdot \left({\sqrt {3}}+1-{\sqrt[{4}]{12}}\right)=\operatorname {cl} \left({\frac {\varpi }{3}}\right)}
sl
(
ϖ
3
)
=
3
8
2
4
⋅
3
−
1
=
cl
(
ϖ
6
)
{\displaystyle \operatorname {sl} \left({\frac {\varpi }{3}}\right)={\frac {\sqrt[{8}]{3}}{\sqrt[{4}]{2}}}\cdot {\sqrt {{\sqrt {3}}-1}}=\operatorname {cl} \left({\frac {\varpi }{6}}\right)}
sl
(
ϖ
8
)
=
(
2
4
−
1
)
⋅
(
2
+
1
−
2
+
2
)
=
cl
(
3
⋅
ϖ
8
)
{\displaystyle \operatorname {sl} \left({\frac {\varpi }{8}}\right)={\sqrt {\left({\sqrt[{4}]{2}}-1\right)\cdot \left({\sqrt {2}}+1-{\sqrt {2+{\sqrt {2}}}}\right)}}=\operatorname {cl} \left({\frac {3\cdot \varpi }{8}}\right)}
sl
(
3
⋅
ϖ
8
)
=
(
2
4
−
1
)
⋅
(
2
+
1
+
2
+
2
)
=
cl
(
ϖ
8
)
{\displaystyle \operatorname {sl} \left({\frac {3\cdot \varpi }{8}}\right)={\sqrt {\left({\sqrt[{4}]{2}}-1\right)\cdot \left({\sqrt {2}}+1+{\sqrt {2+{\sqrt {2}}}}\right)}}=\operatorname {cl} \left({\frac {\varpi }{8}}\right)}
sl
(
ϖ
5
)
=
1
2
⋅
2
4
⋅
(
5
−
1
)
⋅
20
4
−
5
−
1
=
cl
(
3
⋅
ϖ
10
)
{\displaystyle \operatorname {sl} \left({\frac {\varpi }{5}}\right)={\frac {1}{2\cdot {\sqrt[{4}]{2}}}}\cdot ({\sqrt {5}}-1)\cdot {\sqrt {{\sqrt[{4}]{20}}-{\sqrt {{\sqrt {5}}-1}}}}=\operatorname {cl} \left({\frac {3\cdot \varpi }{10}}\right)}
sl
(
2
⋅
ϖ
5
)
=
1
2
⋅
2
4
⋅
(
5
−
1
)
⋅
20
4
+
5
−
1
=
cl
(
ϖ
10
)
{\displaystyle \operatorname {sl} \left({\frac {2\cdot \varpi }{5}}\right)={\frac {1}{2\cdot {\sqrt[{4}]{2}}}}\cdot ({\sqrt {5}}-1)\cdot {\sqrt {{\sqrt[{4}]{20}}+{\sqrt {{\sqrt {5}}-1}}}}=\operatorname {cl} \left({\frac {\varpi }{10}}\right)}
sl
(
ϖ
10
)
=
1
2
⋅
(
5
4
−
1
)
⋅
(
5
+
2
−
1
)
=
cl
(
2
⋅
ϖ
5
)
{\displaystyle \operatorname {sl} \left({\frac {\varpi }{10}}\right)={\frac {1}{2}}\cdot \left({\sqrt[{4}]{5}}-1\right)\cdot \left({\sqrt {{\sqrt {5}}+2}}-1\right)=\operatorname {cl} \left({\frac {2\cdot \varpi }{5}}\right)}
sl
(
3
⋅
ϖ
10
)
=
1
2
⋅
(
5
4
−
1
)
⋅
(
5
+
2
+
1
)
=
cl
(
ϖ
5
)
{\displaystyle \operatorname {sl} \left({\frac {3\cdot \varpi }{10}}\right)={\frac {1}{2}}\cdot \left({\sqrt[{4}]{5}}-1\right)\cdot \left({\sqrt {{\sqrt {5}}+2}}+1\right)=\operatorname {cl} \left({\frac {\varpi }{5}}\right)}
Weitere lemniskatische Funktionswerte in trigonometrischer Darstellung:
sl
(
1
12
ϖ
)
=
1
2
8
4
[
sin
(
5
24
π
)
−
3
4
sin
(
1
24
π
)
]
(
2
3
+
3
4
−
1
)
=
cl
(
5
12
ϖ
)
{\displaystyle \operatorname {sl} {\bigl (}{\tfrac {1}{12}}\varpi {\bigr )}={\tfrac {1}{2}}{\sqrt[{4}]{8}}\left[\sin \left({\tfrac {5}{24}}\pi \right)-{\sqrt[{4}]{3}}\sin \left({\tfrac {1}{24}}\pi \right)\right]\left({\sqrt[{4}]{2{\sqrt {3}}+3}}-1\right)=\operatorname {cl} {\bigl (}{\tfrac {5}{12}}\varpi {\bigr )}}
sl
(
5
12
ϖ
)
=
1
2
8
4
[
sin
(
5
24
π
)
−
3
4
sin
(
1
24
π
)
]
(
2
3
+
3
4
+
1
)
=
cl
(
1
12
ϖ
)
{\displaystyle \operatorname {sl} {\bigl (}{\tfrac {5}{12}}\varpi {\bigr )}={\tfrac {1}{2}}{\sqrt[{4}]{8}}\left[\sin \left({\tfrac {5}{24}}\pi \right)-{\sqrt[{4}]{3}}\sin \left({\tfrac {1}{24}}\pi \right)\right]\left({\sqrt[{4}]{2{\sqrt {3}}+3}}+1\right)=\operatorname {cl} {\bigl (}{\tfrac {1}{12}}\varpi {\bigr )}}
sl
(
1
14
ϖ
)
=
tanh
{
1
2
arcoth
[
1
2
2
cos
(
3
14
π
)
cot
(
1
28
π
)
+
cos
(
1
7
π
)
]
}
=
cl
(
3
7
ϖ
)
{\displaystyle \operatorname {sl} {\bigl (}{\tfrac {1}{14}}\varpi {\bigr )}=\tanh {\bigl \{}{\tfrac {1}{2}}\operatorname {arcoth} {\bigl [}{\tfrac {1}{2}}{\sqrt {2\cos({\tfrac {3}{14}}\pi )\cot({\tfrac {1}{28}}\pi )}}+\cos({\tfrac {1}{7}}\pi ){\bigr ]}{\bigr \}}=\operatorname {cl} {\bigl (}{\tfrac {3}{7}}\varpi {\bigr )}}
sl
(
3
14
ϖ
)
=
tanh
{
1
2
arcoth
[
1
2
2
cos
(
1
14
π
)
tan
(
5
28
π
)
+
sin
(
3
14
π
)
]
}
=
cl
(
2
7
ϖ
)
{\displaystyle \operatorname {sl} {\bigl (}{\tfrac {3}{14}}\varpi {\bigr )}=\tanh {\bigl \{}{\tfrac {1}{2}}\operatorname {arcoth} {\bigl [}{\tfrac {1}{2}}{\sqrt {2\cos({\tfrac {1}{14}}\pi )\tan({\tfrac {5}{28}}\pi )}}+\sin({\tfrac {3}{14}}\pi ){\bigr ]}{\bigr \}}=\operatorname {cl} {\bigl (}{\tfrac {2}{7}}\varpi {\bigr )}}
sl
(
5
14
ϖ
)
=
tanh
{
1
2
arcoth
[
1
2
2
sin
(
1
7
π
)
cot
(
3
28
π
)
+
sin
(
1
14
π
)
]
}
=
cl
(
1
7
ϖ
)
{\displaystyle \operatorname {sl} {\bigl (}{\tfrac {5}{14}}\varpi {\bigr )}=\tanh {\bigl \{}{\tfrac {1}{2}}\operatorname {arcoth} {\bigl [}{\tfrac {1}{2}}{\sqrt {2\sin({\tfrac {1}{7}}\pi )\cot({\tfrac {3}{28}}\pi )}}+\sin({\tfrac {1}{14}}\pi ){\bigr ]}{\bigr \}}=\operatorname {cl} {\bigl (}{\tfrac {1}{7}}\varpi {\bigr )}}
Reihenentwicklungen
Produktreihen nach Whittaker und Watson
Folgende Produktreihen für die lemniskatischen Funktionen konvergieren schnell:
sl
(
x
)
=
2
exp
(
−
1
4
π
)
sin
(
π
x
/
ϖ
)
∏
k
=
1
∞
1
−
2
cos
(
2
π
x
/
ϖ
)
exp
(
−
2
k
π
)
+
exp
(
−
4
k
π
)
1
+
2
cos
(
2
π
x
/
ϖ
)
exp
[
−
(
2
k
−
1
)
π
]
+
exp
[
−
(
4
k
−
2
)
π
]
{\displaystyle \operatorname {sl} (x)=2\exp \left(-{\tfrac {1}{4}}\pi \right)\sin(\pi x/\varpi )\prod _{k=1}^{\infty }{\frac {1-2\cos(2\pi x/\varpi )\exp(-2k\pi )+\exp(-4k\pi )}{1+2\cos(2\pi x/\varpi )\exp[-(2k-1)\pi ]+\exp[-(4k-2)\pi ]}}}
cl
(
x
)
=
2
exp
(
−
1
4
π
)
cos
(
π
x
/
ϖ
)
∏
k
=
1
∞
1
+
2
cos
(
2
π
x
/
ϖ
)
exp
(
−
2
k
π
)
+
exp
(
−
4
k
π
)
1
−
2
cos
(
2
π
x
/
ϖ
)
exp
[
−
(
2
k
−
1
)
π
]
+
exp
[
−
(
4
k
−
2
)
π
]
{\displaystyle \operatorname {cl} (x)=2\exp \left(-{\tfrac {1}{4}}\pi \right)\cos(\pi x/\varpi )\prod _{k=1}^{\infty }{\frac {1+2\cos(2\pi x/\varpi )\exp(-2k\pi )+\exp(-4k\pi )}{1-2\cos(2\pi x/\varpi )\exp[-(2k-1)\pi ]+\exp[-(4k-2)\pi ]}}}
Auf den Forschungsresultaten Edmund Taylor Whittaker und George Neville Watson [ 4] [ 5] [ 6]
Trigonometrisch Hyperbolische Summenreihen
Diese Summen stellen schnell konvergierende Reihen zur numerischen Berechnung des lemniskatischen Sinus und Cosinus dar:[ 7]
sl
(
x
)
=
4
π
ϖ
sin
(
π
x
ϖ
)
∑
k
=
0
∞
(
−
1
)
k
sinh
[
(
k
+
1
/
2
)
π
]
cosh
[
(
2
k
+
1
)
π
]
+
cos
(
2
π
x
/
ϖ
)
,
{\displaystyle \operatorname {sl} (x)={\frac {4\pi }{\varpi }}\sin \left({\frac {\pi x}{\varpi }}\right)\sum _{k=0}^{\infty }{\frac {(-1)^{k}\sinh[(k+1/2)\pi ]}{\cosh[(2k+1)\pi ]+\cos \left(2\pi x/\varpi \right)}},}
cl
(
x
)
=
4
π
ϖ
cos
(
π
x
ϖ
)
∑
k
=
0
∞
(
−
1
)
k
sinh
[
(
k
+
1
/
2
)
π
]
cosh
[
(
2
k
+
1
)
π
]
−
cos
(
2
π
x
/
ϖ
)
,
{\displaystyle \operatorname {cl} (x)={\frac {4\pi }{\varpi }}\cos \left({\frac {\pi x}{\varpi }}\right)\sum _{k=0}^{\infty }{\frac {(-1)^{k}\sinh[(k+1/2)\pi ]}{\cosh[(2k+1)\pi ]-\cos(2\pi x/\varpi )}},}
Hierbei verläuft die Präzision der Annäherung mit endlichem oberen Index
m
{\displaystyle m}
10
−
3
m
/
2
{\displaystyle 10^{-3m/2}}
Beide Reihen zeigen deutlich den Zusammenhang mit den Kreisfunktionen , indem die nach der lemniskatischen Form ausgestreckten Kreisfunktionen als Summanden in den genannten Differenzen gezeigt werden.
Basierend auf der Summendefinition der Jacobischen Zetafunktion können diese nicht alternierenden Summen aufgestellt werden:
tan
{
1
2
arctan
[
sl
(
x
)
]
}
=
4
π
ϖ
sin
(
π
x
/
ϖ
)
∑
k
=
1
∞
cosh
[
(
2
k
−
1
)
π
]
cosh
[
(
2
k
−
1
)
π
]
2
−
cos
(
π
x
/
ϖ
)
2
{\displaystyle \tan \left\{{\frac {1}{2}}\arctan {\bigl [}\operatorname {sl} (x){\bigr ]}\right\}={\frac {4\pi }{\varpi }}\sin(\pi x/\varpi )\sum _{k=1}^{\infty }{\frac {\cosh[(2k-1)\pi ]}{\cosh[(2k-1)\pi ]^{2}-\cos(\pi x/\varpi )^{2}}}}
tan
{
1
2
arctan
[
cl
(
x
)
]
}
=
4
π
ϖ
cos
(
π
x
/
ϖ
)
∑
k
=
1
∞
cosh
[
(
2
k
−
1
)
π
]
cosh
[
(
2
k
−
1
)
π
]
2
−
sin
(
π
x
/
ϖ
)
2
{\displaystyle \tan \left\{{\frac {1}{2}}\arctan {\bigl [}\operatorname {cl} (x){\bigr ]}\right\}={\frac {4\pi }{\varpi }}\cos(\pi x/\varpi )\sum _{k=1}^{\infty }{\frac {\cosh[(2k-1)\pi ]}{\cosh[(2k-1)\pi ]^{2}-\sin(\pi x/\varpi )^{2}}}}
Zusatzinformation:
Die Tangenshalbierungen von Sinus lemniscatus und Cosinus lemniscatus führen zu den Jacobi-Funktionen mit dem Modul λ*(4):
tan
{
1
2
arctan
[
sl
(
x
)
]
}
=
(
2
−
1
)
sn
[
1
2
(
2
+
1
)
x
;
(
2
−
1
)
2
]
{\displaystyle \tan \left\{{\frac {1}{2}}\arctan {\bigl [}\operatorname {sl} (x){\bigr ]}\right\}=({\sqrt {2}}-1)\operatorname {sn} \left[{\tfrac {1}{2}}({\sqrt {2}}+1)x;({\sqrt {2}}-1)^{2}\right]}
tan
{
1
2
arctan
[
cl
(
x
)
]
}
=
(
2
−
1
)
cd
[
1
2
(
2
+
1
)
x
;
(
2
−
1
)
2
]
{\displaystyle \tan \left\{{\frac {1}{2}}\arctan {\bigl [}\operatorname {cl} (x){\bigr ]}\right\}=({\sqrt {2}}-1)\operatorname {cd} \left[{\tfrac {1}{2}}({\sqrt {2}}+1)x;({\sqrt {2}}-1)^{2}\right]}
Rein Hyperbolische Summenreihen
Weitere Reihendarstellungen über alternierende Summen des Secans hyperbolicus lauten so:
ϖ
π
cl
(
ϖ
x
)
=
∑
k
=
−
∞
∞
(
−
1
)
k
sech
[
π
(
k
+
x
)
]
{\displaystyle {\frac {\varpi }{\pi }}\operatorname {cl} (\varpi x)=\sum _{k=-\infty }^{\infty }(-1)^{k}\operatorname {sech} [\pi (k+x)]}
ϖ
π
sl
(
ϖ
x
)
=
∑
k
=
−
∞
∞
(
−
1
)
k
sech
[
π
(
k
−
1
2
+
x
)
]
{\displaystyle {\frac {\varpi }{\pi }}\operatorname {sl} (\varpi x)=\sum _{k=-\infty }^{\infty }(-1)^{k}\operatorname {sech} [\pi (k-{\frac {1}{2}}+x)]}
Definition mit der Ramanujanschen Thetafunktion
Die Ramanujansche Thetafunktion hat diese Definition:
ϑ
R
(
v
;
w
)
=
∑
n
=
−
∞
∞
v
n
(
n
+
1
)
/
2
w
n
(
n
−
1
)
/
2
=
∑
n
=
−
∞
∞
v
△
(
n
)
w
△
(
n
−
1
)
{\displaystyle \vartheta _{R}(v;w)=\sum _{n=-\infty }^{\infty }v^{n(n+1)/2}\,w^{n(n-1)/2}=\sum _{n=-\infty }^{\infty }v^{\bigtriangleup (n)}\,w^{\bigtriangleup (n-1)}}
Der korrespondierende Ausdruck aus einer Summe mit dem Index Eins lautet demnach so:
ϑ
R
(
v
;
w
)
=
1
+
v
+
w
+
∑
n
=
1
∞
(
v
w
)
△
(
n
)
(
v
n
+
1
+
w
n
+
1
)
{\displaystyle \vartheta _{R}(v;w)=1+v+w+\sum _{n=1}^{\infty }(vw)^{\bigtriangleup (n)}(v^{n+1}+w^{n+1})}
So können darauf basierend folgende Identitäten hervorgebracht werden:
1
+
tan
{
1
8
π
−
1
2
arctan
[
s
l
(
x
)
]
}
=
2
exp
(
−
x
G
)
ϑ
R
[
exp
(
x
÷
G
−
1
2
π
)
;
exp
(
−
x
÷
G
−
3
2
π
)
]
2
ϑ
R
[
exp
(
x
÷
G
−
3
2
π
)
;
exp
(
−
x
÷
G
−
1
2
π
)
]
2
{\displaystyle 1+\tan {\biggl \{}{\frac {1}{8}}\pi -{\frac {1}{2}}\arctan {\bigl [}\mathrm {sl} (x){\bigr ]}{\biggr \}}={\sqrt {2}}\exp {\bigl (}-{\frac {x}{G}}{\bigr )}\,{\frac {\vartheta _{R}{\bigl [}\exp(x\div G-{\tfrac {1}{2}}\pi );\exp(-x\div G-{\tfrac {3}{2}}\pi ){\bigr ]}^{2}}{\vartheta _{R}{\bigl [}\exp(x\div G-{\tfrac {3}{2}}\pi );\exp(-x\div G-{\tfrac {1}{2}}\pi ){\bigr ]}^{2}}}}
1
+
tan
{
1
8
π
−
1
2
arctan
[
c
l
(
x
)
]
}
=
2
exp
(
x
G
−
π
2
)
ϑ
R
[
exp
(
−
x
÷
G
)
;
exp
(
x
÷
G
−
2
π
)
]
2
ϑ
R
[
exp
(
−
x
÷
G
−
π
)
;
exp
(
x
÷
G
−
π
)
]
2
{\displaystyle 1+\tan {\biggl \{}{\frac {1}{8}}\pi -{\frac {1}{2}}\arctan {\bigl [}\mathrm {cl} (x){\bigr ]}{\biggr \}}={\sqrt {2}}\exp {\bigl (}{\frac {x}{G}}-{\frac {\pi }{2}}{\bigr )}\,{\frac {\vartheta _{R}{\bigl [}\exp(-x\div G);\exp(x\div G-2\pi ){\bigr ]}^{2}}{\vartheta _{R}{\bigl [}\exp(-x\div G-\pi );\exp(x\div G-\pi ){\bigr ]}^{2}}}}
Noch viel schneller als die Reihen der vorherigen Abschnitte konvergieren somit folgende zwei Reihen für die lemniskatischen Funktionen, welche sich direkt aus den Formeln mit der Ramanujanschen Thetafunktion herleiten lassen:
1
+
tan
{
1
8
π
−
1
2
arctan
[
sl
(
x
)
]
}
=
2
{
∑
k
=
−
∞
∞
exp
[
−
π
(
k
+
1
4
+
x
2
ϖ
)
2
]
}
2
{
∑
k
=
−
∞
∞
exp
[
−
π
(
k
−
1
4
+
x
2
ϖ
)
2
]
}
−
2
{\displaystyle 1+\tan \left\{{\frac {1}{8}}\pi -{\frac {1}{2}}\arctan {\bigl [}\operatorname {sl} (x){\bigr ]}\right\}={\sqrt {2}}\,\left\{\sum _{k=-\infty }^{\infty }\exp \left[-\pi \left(k+{\frac {1}{4}}+{\frac {x}{2\varpi }}\right)^{2}\right]\right\}^{2}\left\{\sum _{k=-\infty }^{\infty }\exp \left[-\pi \left(k-{\frac {1}{4}}+{\frac {x}{2\varpi }}\right)^{2}\right]\right\}^{-2}}
1
+
tan
{
1
8
π
−
1
2
arctan
[
cl
(
x
)
]
}
=
2
{
∑
k
=
−
∞
∞
exp
[
−
π
(
k
+
1
2
+
x
2
ϖ
)
2
]
}
2
{
∑
k
=
−
∞
∞
exp
[
−
π
(
k
+
x
2
ϖ
)
2
]
}
−
2
{\displaystyle 1+\tan \left\{{\frac {1}{8}}\pi -{\frac {1}{2}}\arctan {\bigl [}\operatorname {cl} (x){\bigr ]}\right\}={\sqrt {2}}\,\left\{\sum _{k=-\infty }^{\infty }\exp \left[-\pi \left(k+{\frac {1}{2}}+{\frac {x}{2\varpi }}\right)^{2}\right]\right\}^{2}\left\{\sum _{k=-\infty }^{\infty }\exp \left[-\pi \left(k+{\frac {x}{2\varpi }}\right)^{2}\right]\right\}^{-2}}
Elliptische Lambdafunktion
Diejenigen elliptischen Module, welche die Lambda-Stern-Funktionswerte von den Doppelten der ungeraden natürlichen Zahlen[ 8]
Weitere Werte:
λ
∗
(
14
)
=
sl
{
1
2
arcsl
[
(
8
2
+
11
)
−
1
/
2
]
}
2
{\displaystyle \lambda ^{*}(14)=\operatorname {sl} \left\{{\tfrac {1}{2}}\operatorname {arcsl} \left[(8{\sqrt {2}}+11)^{-1/2}\right]\right\}^{2}}
λ
∗
(
26
)
=
sl
{
1
2
arcsl
[
1
33
(
2
132
78
+
837
3
−
2
132
78
−
837
3
−
9
)
]
}
2
{\displaystyle \lambda ^{*}(26)=\operatorname {sl} \left\{{\tfrac {1}{2}}\operatorname {arcsl} \left[{\tfrac {1}{33}}\left(2{\sqrt[{3}]{132{\sqrt {78}}+837}}-2{\sqrt[{3}]{132{\sqrt {78}}-837}}-9\right)\right]\right\}^{2}}
λ
∗
(
38
)
=
sl
{
1
2
arcsl
[
1
627
19
(
2
3300
114
+
27323
3
−
2
3300
114
−
27323
3
−
35
)
]
}
2
{\displaystyle \lambda ^{*}(38)=\operatorname {sl} \left\{{\tfrac {1}{2}}\operatorname {arcsl} \left[{\tfrac {1}{627}}{\sqrt {19}}\left(2{\sqrt[{3}]{3300{\sqrt {114}}+27323}}-2{\sqrt[{3}]{3300{\sqrt {114}}-27323}}-35\right)\right]\right\}^{2}}
λ
∗
(
46
)
=
sl
{
1
2
arcsl
[
1
3
(
104
2
+
147
)
−
1
/
2
]
}
2
{\displaystyle \lambda ^{*}(46)=\operatorname {sl} \left\{{\tfrac {1}{2}}\operatorname {arcsl} \left[{\tfrac {1}{3}}(104{\sqrt {2}}+147)^{-1/2}\right]\right\}^{2}}
λ
∗
(
66
)
=
sl
{
1
2
arcsl
[
(
75
2
+
13
2
33
+
1
2
1842
33
+
10578
)
−
1
]
}
2
{\displaystyle \lambda ^{*}(66)=\operatorname {sl} \left\{{\tfrac {1}{2}}\operatorname {arcsl} \left[\left({\tfrac {75}{2}}+{\tfrac {13}{2}}{\sqrt {33}}+{\tfrac {1}{2}}{\sqrt {1842{\sqrt {33}}+10578}}\right)^{-1}\right]\right\}^{2}}
Zusammenhang mit anderen Funktionen
Die lemniskatischen Funktionen sind eng verwandt mit der weierstraßschen ℘-Funktion
℘
(
z
;
1
,
0
)
{\displaystyle \wp (z;1,0)}
g
2
=
1
{\displaystyle g_{2}=1}
g
3
=
0
{\displaystyle g_{3}=0}
ω
1
=
2
ϖ
{\displaystyle \omega _{1}={\sqrt {2}}\varpi }
ω
2
=
i
ω
1
=
i
2
ϖ
{\displaystyle \omega _{2}=\mathrm {i} \omega _{1}=\mathrm {i} {\sqrt {2}}\varpi }
e
1
=
1
2
{\displaystyle e_{1}={\tfrac {1}{2}}}
e
2
=
0
{\displaystyle e_{2}=0}
e
3
=
−
1
2
.
{\displaystyle e_{3}=-{\tfrac {1}{2}}.}
Der verwandte Fall einer weierstraßschen ℘-Funktion mit
g
2
=
a
{\displaystyle g_{2}=a}
g
3
=
0
{\displaystyle g_{3}=0}
a
>
0
{\displaystyle a>0}
a
<
0
{\displaystyle a<0}
Quadrat oder eine Raute . Bei der weierstraßschen ℘-Funktion
℘
(
z
;
−
1
,
0
)
{\displaystyle \wp (z;-1,0)}
Das Quadrat des lemniskatischen Sinus kann ausgedrückt werden durch
sl
2
z
=
1
℘
(
z
;
4
,
0
)
=
i
2
℘
(
(
1
−
i
)
z
;
−
1
,
0
)
=
−
2
℘
(
2
z
+
(
i
−
1
)
ϖ
2
;
1
,
0
)
.
{\displaystyle \operatorname {sl} ^{2}z={\frac {1}{\wp (z;4,0)}}={\frac {i}{2\wp ((1-i)z;-1,0)}}={-2\wp }{\left({\sqrt {2}}z+(i-1){\frac {\varpi }{\sqrt {2}}};1,0\right)}.}
wobei das zweite und dritte Argument von
℘
{\displaystyle \wp }
g
2
{\displaystyle g_{2}}
g
3
{\displaystyle g_{3}}
rationale Funktion bezüglich der weierstraßschen ℘-Funktion und deren Ableitung:[ 9]
sl
z
=
−
2
℘
(
z
;
−
1
,
0
)
℘
′
(
z
;
−
1
,
0
)
.
{\displaystyle \operatorname {sl} z=-2{\frac {\wp (z;-1,0)}{\wp '(z;-1,0)}}.}
Die lemniskatischen Funktionen lassen sich auch durch jacobische elliptische Funktionen ausdrücken. Die jacobischen elliptischen Funktionen
sn
{\displaystyle \operatorname {sn} }
cd
{\displaystyle \operatorname {cd} }
sn
{\displaystyle \operatorname {sn} }
cd
{\displaystyle \operatorname {cd} }
i
{\displaystyle \mathrm {i} }
sd
{\displaystyle \operatorname {sd} }
cn
{\displaystyle \operatorname {cn} }
1
/
2
{\displaystyle 1/{\sqrt {2}}}
45
∘
{\displaystyle 45^{\circ }}
[ 10] [ 11]
sl
z
=
sn
(
z
;
i
)
=
sc
(
z
;
2
)
=
1
2
sd
(
2
z
;
1
2
)
,
{\displaystyle \operatorname {sl} z=\operatorname {sn} (z;\mathrm {i} )=\operatorname {sc} (z;{\sqrt {2}})={{\tfrac {1}{\sqrt {2}}}\operatorname {sd} }\left({\sqrt {2}}z;{\tfrac {1}{\sqrt {2}}}\right),}
cl
z
=
cd
(
z
;
i
)
=
dn
(
z
;
2
)
=
cn
(
2
z
;
1
2
)
,
{\displaystyle \operatorname {cl} z=\operatorname {cd} (z;\mathrm {i} )=\operatorname {dn} (z;{\sqrt {2}})={\operatorname {cn} }\left({\sqrt {2}}z;{\tfrac {1}{\sqrt {2}}}\right),}
wobei das zweite Argument jeweils den elliptischen Modul
k
{\displaystyle k}
Siehe auch
Literatur
Weblinks
Einzelnachweise
↑ Derivative of the Jacobi theta function: Introduction to the Jacobi theta functions. Abgerufen am 1. August 2021 . ↑ H. A. Schwarz: Über einige Abbildungsaufgaben. Abgerufen am 2. August 2025 . ↑ Die Nullstellen sind schwarz gezeichnet, die Polstellen weiß. Wenn das Argument von
sl
z
{\displaystyle \operatorname {sl} z}
−
π
{\displaystyle -\pi }
π
{\displaystyle \pi }
(
Arg
≈
−
π
/
2
)
{\displaystyle (\operatorname {Arg} \approx -\pi /2)}
(
Arg
≈
0
)
{\displaystyle (\operatorname {Arg} \approx 0)}
(
Arg
≈
π
/
2
)
{\displaystyle (\operatorname {Arg} \approx \pi /2)}
(
Arg
≈
π
)
{\displaystyle (\operatorname {Arg} \approx \pi )}
↑ Eric W. Weisstein : Jacobi Theta Functions .MathWorld ↑ http://wayback.cecm.sfu.ca/~pborwein/TEMP_PROTECTED/pi-agm.pdf ↑ DLMF: 20.5 Infinite Products and Related Results. Abgerufen am 13. August 2022 . ↑ https://www.mdpi.com/2073-8994/12/6/1040 ↑ Eric W. Weisstein : Elliptic Lambda Function .MathWorld ↑ Pierre Eymard, Jean-Pierre Lafon: The Number Pi . American Mathematical Society, 2004, ISBN 0-8218-3246-8, S. 234 (englisch).
↑ J. V. Armitage, W. F. Eberlein: Elliptic Functions . Cambridge University Press, 2006, ISBN 0-521-78563-4, S. 49 (englisch).
↑ Die Identität
cl
z
=
cn
(
2
z
;
1
2
)
{\displaystyle \operatorname {cl} z={\operatorname {cn} }\left({\sqrt {2}}z;{\tfrac {1}{\sqrt {2}}}\right)}
The Applications of Elliptic Functions . MacMillan (englisch, archive.org [abgerufen am 10. August 2025]).