Komplanarität
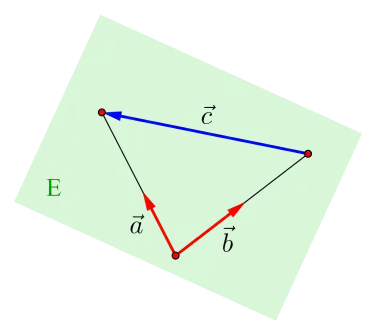
Komplanarität (auch Koplanarität oder Coplanarität, von lat. co- und planar „in der selben Ebene liegend“) ist ein Begriff aus der Analytischen Geometrie, einem Teilgebiet der Mathematik. Drei verschiedene Punkte, die nicht auf einer gemeinsamen Geraden liegen, erzeugen eindeutig eine Ebene, in der sie liegen.[1] Mehr als drei Punkte sind komplanar, wenn sie in einer gemeinsamen Ebene liegen.[2] Entsprechend sind drei Vektoren komplanar, wenn sie in derselben Ebene liegen.[3] Dies ist genau dann der Fall, wenn sich einer der Vektoren als Linearkombination der anderen beiden darstellen lässt, d. h. wenn die drei Vektoren linear abhängig sind.
Komplanaritätsuntersuchung
In der linearen Algebra bedeutet Komplanarität bei Vektoren eines Vektorraums, dass der von diesen Vektoren aufgespannte Untervektorraum die Dimension 2 hat. Zur Prüfung der Komplanarität von Vektoren kann eine Komplanaritätsuntersuchung durchgeführt werden. Hierfür gibt es mehrere Möglichkeiten:
Bei drei komplanaren Vektoren muss sich einer von ihnen als Linearkombination der beiden anderen darstellen lassen. Gelingt es zum Beispiel zu zeigen, dass für reelle Zahlen und gilt, so sind die Vektoren komplanar. Die Prüfung läuft dann auf das Lösen eines linearen Gleichungssystems mit drei Gleichungen und zwei Unbekannten hinaus.
Bei drei komplanaren Vektoren muss die Gleichung eine Lösung haben, bei der nicht alle null sind. Die Prüfung läuft dann auf das Lösen eines linearen Gleichungssystems mit drei Gleichungen und drei Unbekannten hinaus.[4]
Entstammen die Vektoren einem dreidimensionalen Vektorraum, so lässt sich diese Prüfung mit dem Spatprodukt durchführen: Die Vektoren sind genau dann komplanar, wenn ihr Spatprodukt ist. Auch gilt dann .
Beispiel
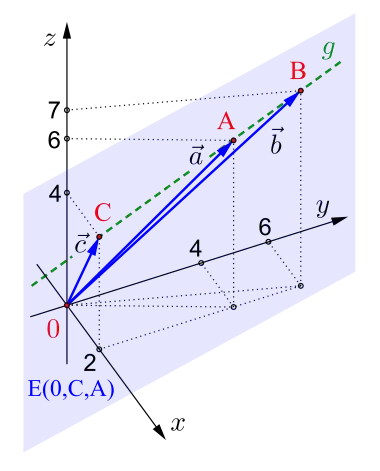
Die drei Vektoren und liegen auf der Ebene und sind somit komplanar.
Drei Vektoren und sollen auf Komplanarität untersucht werden.
Ansatz:
mit .
Aus dem Ansatz folgt das lineare Gleichungssystem:
Aus Gleichung folgt . Einsetzen in Gleichung und Umstellen liefert . Gleichung ist für und wegen erfüllt. Somit ist eine Linearkombination von und ,
- ,
und , und sind komplanar.
Kollineare Vektoren sind immer auch komplanar, es gibt unendlich viele Ebenen, in denen sie liegen können. Ersetzt man zum Beispiel den obigen Vektor durch , dann sind die Vektoren und kollinear. Eine Komplanaritätsuntersuchung der drei Vektoren und nach obigem Vorbild ergibt dann und als Lösungen des neuen Gleichungssystems, woraus die Kollinearität der beiden Vektoren und folgt. Versucht man dagegen den Vektor als Linearkombination der beiden anderen darzustellen, so sieht man auch ohne Rechnung, dass dies unmöglich ist, da diese beiden Vektoren keine Basis des durch und erzeugten zweidimensionalen Vektorraums sind.
Verwendung
Komplanaritätsuntersuchungen werden häufig bei der Ermittlung der Lagebeziehungen zwischen Geraden oder Geraden und Ebenen durchgeführt.
In der Chemie ist z. B. bei Kongeneren von polychlorierten Biphenylen (PCB) die Coplanarität ein wichtiges Kriterium für deren Toxizität: Coplanare bzw. dioxinähnliche PCB sind deutlich toxischer.[5]
Einzelnachweise
- ↑ Tilo Arens und andere: Mathematik. 5. Auflage. Springer, 2022, ISBN 978-3-662-64388-4, S. 566.
- ↑ Chr. Dürr und andere: Analytische Geometrie Leistungskurs. Volk und Wissen Verlag, Berlin 1998, ISBN 978-3-06-001173-5, S. 78.
- ↑ Chr. Dürr und andere: Analytische Geometrie Leistungskurs. Volk und Wissen Verlag, Berlin 1998, ISBN 978-3-06-001173-5, S. 55.
- ↑ H. Krämer, R. Höwelmann, I. Klemisch: Analytische Geometrie und Lineare Algebra. Verlag Moritz Diesterweg, Frankfurt am Main 1989, ISBN 3-425-05301-9, S. 75 – 82.
- ↑ Chlorierte Biphenyle [MAK Value Documentation in German language, 2013]. In: The MAK-Collection for Occupational Health and Safety. Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim 2013, ISBN 978-3-527-60041-0, S. 1–139, doi:10.1002/3527600418.mb0cbphpcbd0055.