Inverse Normalverteilung

Die inverse Normalverteilung (auch inverse Gauß-Verteilung oder Wald-Verteilung genannt) ist eine kontinuierliche Wahrscheinlichkeitsverteilung. Sie wird in verallgemeinerten linearen Modellen verwendet. Bei der Untersuchung der Brownschen Molekularbewegung mit Drift ${\displaystyle v>0}$ und Streuungskoeffizient ${\displaystyle \lambda >0}$ ist die zufällige Zeit des ersten Erreichens des Niveaus ${\displaystyle a>0}$ invers normalverteilt mit den Parametern ${\displaystyle \left({\frac {a}{v}},{\frac {a^{2}}{\lambda ^{2}}}\right)}$. Die inverse Normalverteilung gehört zur Exponentialfamilie.

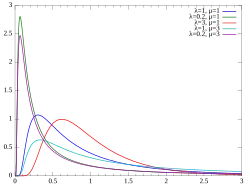
Eine stetige Zufallsvariable ${\displaystyle X}$ genügt der inversen Normalverteilung mit den Parametern ${\displaystyle \lambda >0}$ (Ereignisrate) und ${\displaystyle \mu >0}$ (Erwartungswert), wenn sie die Wahrscheinlichkeitsdichte ${\displaystyle f(x)={\begin{cases}\left({\frac {\lambda }{2\pi x^{3}}}\right)^{\frac {1}{2}}e^{-{\frac {\lambda (x-\mu )^{2}}{2\mu ^{2}x}}}&x>0\\0&x\leq 0\end{cases}}}$ besitzt.

Die Verteilungsfunktion ist gegeben als

${\displaystyle F(x)=IG(x;{\frac {\mu }{\sqrt {\lambda }}};{\sqrt {\lambda }}):=1-\Phi ({\frac {\sqrt {\lambda }}{\sqrt {x}}}-{\frac {\mu }{\sqrt {\lambda }}}{\sqrt {x}})+e^{2\mu }\Phi (-{\frac {\sqrt {\lambda }}{\sqrt {x}}}-{\frac {\mu }{\sqrt {\lambda }}}{\sqrt {x}}).}$

Die inverse Normalverteilung besitzt den Erwartungswert

${\displaystyle \operatorname {E} (X)=\mu }$.

Die Varianz ergibt sich analog zu

${\displaystyle \operatorname {Var} (X)={\frac {\mu ^{3}}{\lambda }}}$.

Daraus erhält man für die Standardabweichung

${\displaystyle \sigma ={\sqrt {\frac {\mu ^{3}}{\lambda }}}}$

Aus Erwartungswert und Varianz erhält man unmittelbar den Variationskoeffizienten

${\displaystyle \operatorname {VarK} (X)={\sqrt {\frac {\mu }{\lambda }}}}$.

Die Schiefe ergibt sich zu

${\displaystyle \operatorname {v} (X)=3{\sqrt {\frac {\mu }{\lambda }}}}$.

Die Wölbung ergibt sich zu

${\displaystyle \beta _{2}={\frac {15\mu }{\lambda }}+3}$.

Die Exzess-Kurtosis ist

${\displaystyle \gamma _{2}=\beta _{2}-3={\frac {15\mu }{\lambda }}}$.

Die charakteristische Funktion hat die Form

${\displaystyle \phi _{X}(s)=e^{{\frac {\lambda }{\mu }}\left(1-{\sqrt {1-{\frac {2\mu ^{2}is}{\lambda }}}}\right)}}$.

Die momenterzeugende Funktion der inversen Normalverteilung ist

${\displaystyle m_{X}(s)=e^{{\frac {\lambda }{\mu }}\left(1-{\sqrt {1-{\frac {2\mu ^{2}s}{\lambda }}}}\right)}}$.

Sind ${\displaystyle X_{1},\dots ,X_{n}}$ Zufallsvariable mit inverser Normalverteilung mit den Parametern ${\displaystyle \lambda }$ und ${\displaystyle \mu }$, dann ist die Größe ${\displaystyle {\frac {1}{n}}\sum \limits _{i=1}^{n}X_{i}}$ wieder eine Zufallsvariable mit einer inversen Normalverteilung, aber mit den Parametern ${\displaystyle n\lambda }$ und ${\displaystyle \mu }$.

Die Laplacetransformation der inversen Normalverteilung ist

${\displaystyle \mathbb {E} [e^{-\lambda T}]=\int _{0}^{\infty }e^{-\lambda t}{\text{IG}}({\text{d}}t;\zeta ;u)=\exp\{-u({\sqrt {2\lambda +\zeta ^{2}}}-\zeta )\}.}$

In der Versicherungsmathematik kann zur Berechnung der Ruinwahrscheinlichkeit die zeitliche Verteilung der Schäden mithilfe des Satzes von Donsker durch eine Brownsche Bewegung approximiert werden. Die dadurch approximierten Ruinwahrscheinlichkeiten basieren auf speziellen Parametrisierungen der inversen Normalverteilung.

• Hansjörg Asmussen, Søren Albrecher. Ruin Probabilities (Second Edition). World Scientific Publishing Co. Pte. Ltd., 2010, ISBN 978-981-320-361-7, Kapitel 5, S. 136–145.
• William Feller. Wiley Series in Probability and Mathematical Statistics, Volume II (Second Edition). New York, NY: Dover Publications, 1971, ISBN 978-0-471-25709-7, Kapitel VIII, S. 436–437, 463.

• Eric W. Weisstein: Inverse Gaussian Distribution. In: MathWorld (englisch).