Fock-Zustand
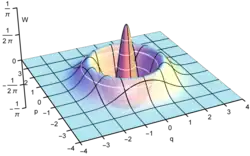
Fock-Zustände (benannt nach dem Physiker Wladimir Alexandrowitsch Fock) sind in der quantenmechanischen Vielteilchentheorie und Quantenfeldtheorie Zustände bestimmter Teilchenzahl im Fock-Raum, die dort als Basis dienen können.
Allgemein wird bei Teilchen unterschieden zwischen
Sie unterscheiden sich wesentlich durch die Vertauschungsrelationen der sie darstellenden Operatoren, ihre Quantenstatistik:
- Fermionen (wie das Elektron) können nach der Fermi-Dirac-Statistik einen Zustand mit gleichen Quantenzahlen (wozu auch ihre Spinausrichtung zählt) im Fock-Raum entweder gar nicht oder nur einmal besetzen.
- Bei Bosonen (wie Photonen oder Phononen) gibt es nach der Bose-Einstein-Statistik keine Beschränkung für die Anzahl der Teilchen in einem bestimmten Zustand.
Zustände im Fock-Raum werden mit Hilfe von Erzeugungs- und Vernichtungsoperatoren aufgebaut. Man spricht auch von Besetzungszahl-Darstellung oder Zweiter Quantisierung.
Im Fock-Raum lassen sich auch Zustände konstruieren, in denen die Teilchenzahl nur im Mittel vorgegeben ist und um den Mittelwert schwanken kann, zum Beispiel kohärente Zustände in der Laserphysik.
Weblinks
- Kohärente Zustände ( vom 26. September 2015 im Internet Archive)
- Crashkurs Photonenstatistik ( vom 10. Oktober 2019 im Internet Archive)
- Röhrl:Stabilität und Instabilität des relativistischen Elektronen-Positronen-Felds in Hartree-Fock-Näherung ( vom 25. September 2015 im Internet Archive)
- Vorlesung Hartree-Fock ( vom 20. Oktober 2022 im Internet Archive)