Flächengeschwindigkeit

Die Flächengeschwindigkeit ist in der Kinematik die Fläche, die der Fahrstrahl zu einem sich bewegenden Punkt pro Zeiteinheit überstreicht.^[1]:26

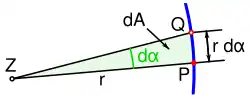
In der Skizze bewegt sich ein Punkt auf der Bahnkurve (blau) um den ruhenden Punkt Z in einer (infinitesimal) kurzen Zeitspanne dt von P nach Q. Der Fahrstrahl r überstreicht in dieser Zeitspanne die Fläche dA, die in erster Näherung den Inhalt^[1]:26

${\displaystyle \mathrm {d} A={\frac {r\cdot (r\,\mathrm {d} \alpha )}{2}}={\frac {r^{2}}{2}}\,\mathrm {d} \alpha }$

besitzt.

Die Bildung des Differenzialquotienten mit der Zeit t liefert die Flächengeschwindigkeit ${\displaystyle {\dot {A}}}$:

${\displaystyle {\dot {A}}:={\frac {\mathrm {d} A}{\mathrm {d} t}}={\frac {r^{2}}{2}}\,{\frac {\mathrm {d} \alpha }{\mathrm {d} t}}=:{\frac {r^{2}}{2}}\,{\dot {\alpha }}}$

${\displaystyle {\dot {\alpha }}}$ ist die Winkelgeschwindigkeit.

Die SI-Einheit ist Quadratmeter pro Sekunde (m²/s) und die Dimension ist Längenquadrat pro Zeit (L² T ⁻¹).

Johannes Keppler benutzte die Flächengeschwindigkeit in seinem Zweiten Keplerschen Gesetz. Seine Formulierung lautete, dass der Fahrstrahl in gleich großen Zeiteinheiten gleich große Flächen überstreicht.

Der Drallsatz für einen Massenpunkt kann mit der Zeitableitung seiner Flächengeschwindigkeit formuliert werden, siehe #Zusammenhang mit dem Drehimpuls und Drallsatz#Flächensatz.

In Polarkoordinaten (ρ,φ) mit Abstandskoordinate ρ vom Ursprung und Polarwinkel φ wird der Fahrstrahl mittels

${\displaystyle {\vec {r}}=\rho \,{\hat {e}}_{\rho }}$

ausgedrückt. Die Zeitableitungen der Basisvektoren ${\displaystyle {\hat {e}}_{\rho ,\varphi }}$ lauten ${\displaystyle {\dot {\hat {e}}}_{\rho }={\dot {\varphi }}{\hat {e}}_{\varphi }}$ bzw. ${\displaystyle {\dot {\hat {e}}}_{\varphi }=-{\dot {\varphi }}{\hat {e}}_{\rho }}$, siehe Ortsvektor, Geschwindigkeit und Beschleunigung in Zylinderkoordinaten. Damit berechnen sich die Geschwindigkeit und die Beschleunigung zu:^[1]:24

${\displaystyle {\begin{aligned}{\vec {v}}:=&{\dot {\vec {r}}}={\dot {\rho }}\,{\hat {e}}_{\rho }+\rho {\dot {\hat {e}}}_{\rho }={\dot {\rho }}\,{\hat {e}}_{\rho }+\rho {\dot {\varphi }}{\hat {e}}_{\varphi }\\{\vec {a}}:=&{\dot {\vec {v}}}={\ddot {\rho }}{\hat {e}}_{\rho }+{\dot {\rho }}{\dot {\hat {e}}}_{\rho }+{\dot {\rho }}{\dot {\varphi }}{\hat {e}}_{\varphi }+\rho {\ddot {\varphi }}{\hat {e}}_{\varphi }+\rho {\dot {\varphi }}{\dot {\hat {e}}}_{\varphi }=:a_{\rho }{\hat {e}}_{\rho }+a_{\varphi }{\hat {e}}_{\varphi }\\&a_{\rho }:={\ddot {\rho }}-\rho {\dot {\varphi }}^{2}\,,\quad a_{\varphi }:=\rho {\ddot {\varphi }}+2{\dot {\rho }}{\dot {\varphi }}={\frac {1}{\rho }}{\frac {\mathrm {d} }{\mathrm {d} t}}(\rho ^{2}{\dot {\varphi }})\end{aligned}}}$

Die Flächengeschwindigkeit bezüglich des Ursprungs ergibt sich wie in der Einleitung zu ${\displaystyle {\dot {A}}={\tfrac {\rho ^{2}}{2}}{\dot {\varphi }}}$. Wenn die zirkulare Beschleunigungskomponente gemäß a_φ=0 verschwindet, wie beispielsweise beim Massenpunkt im Zentralkraftfeld, dann ist die Flächengeschwindigkeit somit konstant.

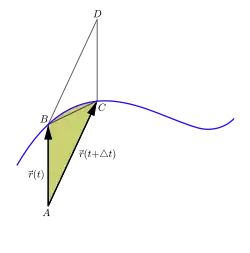
Im Allgemeinen ist die Bahnkurve eines Partikels eine Kurve im Raum, und die Fläche, die der Fahrstrahl mit der Zeit überstreicht, nicht mehr eben. Das Oberflächenelement in einem Punkt einer Fläche ist ein Vektor, der senkrecht auf der Tangentialebene in dem Punkt ist und dessen Betrag der Größe des Flächenstücks entspricht. Dieser Vektor entsteht aus dem Kreuzprodukt × zweier Tangenten im Punkt, die hier angegeben werden können:^[1]:61

1. der Fahrstrahl ${\displaystyle {\vec {r}}={\overrightarrow {AB}}}$ des Punktes B und
2. die Geschwindigkeit dieses Punktes ${\displaystyle {\vec {v}}:={\dot {\vec {r}}}:={\frac {\mathrm {d} {\vec {r}}}{\mathrm {d} t}}:=\lim _{\Delta t\to 0}{\frac {{\vec {r}}(t+\Delta t)-{\vec {r}}(t)}{\Delta t}}}$

Die vektorielle Flächengeschwindigkeit lautet damit:

${\displaystyle {\dot {\vec {A}}}:=\lim _{\Delta t\to 0}{\frac {{\vec {r}}(t)\times {\vec {r}}(t+\Delta t)}{2\Delta t}}={\frac {1}{2}}{\vec {r}}(t)\times \lim _{\Delta t\to 0}{\frac {{\vec {r}}(t+\Delta t)-{\vec {r}}(t)}{\Delta t}}={\frac {1}{2}}({\vec {r}}\times {\vec {v}})}$

Sie entspricht bei (infinitesimal) kleinem Zeitintervall 𝚫t der olivgrünen Fläche im Bild, siehe Geometrische Definition des Kreuzprodukts × (die Fläche ${\displaystyle {\vec {A}}}$ ist hier nicht zu verwechseln mit dem Punkt A.) Nach der Rechte-Hand-Regel ragt dieser Vektor im Bild in die Bildebene hinein (und nicht aus ihr heraus). Demnach trägt weder die zum Fahrstrahl parallele Komponente der Geschwindigkeit noch die Krümmung der Bahnkurve zur Flächengeschwindigkeit etwas bei, was in der Einleitung mit Gleichheit in erster Ordnung angedeutet wurde.

Der Drallsatz angewendet auf einen seiner Bahnkurve folgenden Massenpunkt kann mit seiner Flächengeschwindigkeit ausgedrückt werden:

Das resultierende Moment ist gleich dem Doppelten des Produktes aus der Masse und der Ableitung der Flächengeschwindigkeit.^[2]

Bezüglich des ruhenden Punktes A im Bild (nicht zu verwechseln mit der Fläche ${\displaystyle {\vec {A}}}$) hat ein Massenpunkt B mit Masse m und Geschwindigkeit ${\displaystyle {\dot {\vec {r}}}={\vec {v}}}$ den Impuls ${\displaystyle {\vec {p}}=m{\vec {v}}}$ und den Drehimpuls

${\displaystyle {\vec {L}}_{A}={\vec {r}}\times {\vec {p}}=m\,{\vec {r}}\times {\vec {v}}=2m{\frac {1}{2}}({\vec {r}}\times {\vec {v}})=2m{\dot {\vec {A}}}}$.

Der Drehimpuls des Massenpunkts ist demnach gleich dem Doppelten des Produktes aus der Masse und der Flächengeschwindigkeit. Mit dem Drallsatz ${\displaystyle {\vec {M}}_{A}={\dot {\vec {L}}}_{A}}$ wird daraus

${\displaystyle {\vec {M}}_{A}={\dot {\vec {L}}}_{A}=2m{\ddot {\vec {A}}}}$

was obiger Aussage entspricht. Bei einem ausgedehnten Körper gilt dies nur, wenn

• er keinen Eigendrehimpuls besitzt, sich somit nicht um eine Achse dreht, die durch sein Gravizentrum führt und durch das Moment auch nicht dazu angeregt wird, oder allgemeiner
• sein Eigendrehimpuls keinen nennenswerten Beitrag leistet, wie es bei den Planetenbewegungen im Sonnensystem der Fall ist.^[3][4]

1. ↑ ^{a b c d} D. Gross, W. Hauger, J. Schröder, W. A. Wall: Technische Mechanik 3. Kinetik. Springer Vieweg Verlag, Heidelberg 2015, ISBN 978-3-642-53953-4, S. 26,61, doi:10.1007/978-3-642-53954-1. 
2. ↑ Karl-Heinrich Grote, Jörg Feldhusen (Hrsg.): Dubbel. Taschenbuch für den Maschinenbau. Springer Vieweg Verlag, Berlin, Heidelberg 2014, ISBN 978-3-642-38891-0, S. B26, doi:10.1007/978-3-642-38891-0 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 13. Januar 2018]). 
3. ↑ Gottfried Falk: Theoretische Physik auf der Grundlage einer allgemeinen Dynamik. Elementare Punktmechanik. 1. Band. Springer-Verlag, Berlin, Heidelberg 1966, DNB 456597212, S. 1 f., doi:10.1007/978-3-642-94958-6. 
4. ↑ Georg Hamel: Elementare Mechanik. Ein Lehrbuch. B. G. Teubner, Leipzig und Berlin 1912, S. 66 f. (archive.org [abgerufen am 26. Februar 2020]).