Fakultät (Mathematik)
| 0! | 1 |
| 1! | 1 |
| 2! | 2 |
| 3! | 6 |
| 4! | 24 |
| 5! | 120 |
| 6! | 720 |
| 7! | 5.040 |
| 8! | 40.320 |
| 9! | 362.880 |
| 10! | 3.628.800 |
| 11! | 39.916.800 |
| 12! | 479.001.600 |
| 13! | 6.227.020.800 |
| 14! | 87.178.291.200 |
| 15! | 1.307.674.368.000 |
| 16! | 20.922.789.888.000 |
| 17! | 355.687.428.096.000 |
| 18! | 6.402.373.705.728.000 |
| 19! | 121.645.100.408.832.000 |
| 20! | 2.432.902.008.176.640.000 |
| 50! | 3,041… · 10 64 |
| 100! | 9,332… · 10157 |
Die Fakultät (manchmal, besonders in Österreich, auch Faktorielle genannt) ist in der Mathematik diejenige Funktion, die jeder natürlichen Zahl das Produkt aller positiven natürlichen Zahlen zuordnet, die diese Zahl nicht übertreffen. Sie wird durch ein dem Funktionsargument nachgestelltes Ausrufezeichen („!“) abgekürzt. Ihre Notation mit dem Ausrufezeichen wurde erstmals 1808 von dem elsässischen Mathematiker Christian Kramp (1760–1826) verwendet, der um 1798 auch die Bezeichnung faculté (französisch „Fähigkeit“) dafür einführte.[1]
Definition
Für jede natürliche Zahl ist die Fakultät von n definiert als das Produkt der natürlichen Zahlen von 1 bis :[2]
Da das leere Produkt stets gleich 1 ist, gilt
- .
Die Fakultät lässt sich auch rekursiv definieren:[3]
Die Werte der Fakultäten bilden die Folge A000142 in OEIS.
Beispiele
Die ersten fünf Fakultätswerte lauten
Anwendungen
Permutationen
In der abzählenden Kombinatorik spielen Fakultäten eine wichtige Rolle, weil die Anzahl der Möglichkeiten ist, unterscheidbare Gegenstände in einer Reihe anzuordnen. Falls eine -elementige Menge ist, so ist auch die Anzahl der bijektiven Abbildungen , also die Anzahl der Permutationen von . Dies gilt insbesondere auch für den Fall , da es genau eine Möglichkeit gibt, die leere Menge auf sich selbst abzubilden.
Beispielsweise gibt es bei einem Autorennen mit sechs Fahrern verschiedene Möglichkeiten für die Reihenfolge beim Zieleinlauf, wenn alle Fahrer das Ziel erreichen. Für den ersten Platz kommen alle sechs Fahrer in Frage. Ist der erste Fahrer angekommen, können nur noch fünf Fahrer um den zweiten Platz konkurrieren. Für die Belegung des zweiten Platzes ist es maßgeblich, welcher der sechs Fahrer nicht berücksichtigt werden muss (da er bereits auf Rang 1 platziert ist). Daher muss für jede Belegungsmöglichkeit von Platz 1 gesondert gezählt werden, wie viele Belegungsmöglichkeiten für Platz 2 bestehen. Für die Belegung der Plätze 1 und 2 ergeben sich bei sechs Fahrern daher Möglichkeiten. Ist auch der zweite Platz vergeben, kommen für den dritten Platz nur noch vier Fahrer in Frage, woraus sich für die ersten drei Plätze und sechs Fahrer Belegungsmöglichkeiten ergeben usw. Letztlich gibt es also
verschiedene Ranglisten für den Zieleinlauf.
Binomialkoeffizienten
Ein Begriff, der in der abzählenden Kombinatorik eine ähnlich zentrale Stellung wie die Fakultät einnimmt, ist der Binomialkoeffizient
- .
Er gibt die Anzahl der Möglichkeiten an, aus einer -elementigen Menge eine -elementige Teilmenge auszuwählen.
Zum Beispiel gibt es beim Zahlenlotto 6 aus 49 insgesamt 13.983.816 mögliche Ziehungen:
- .
Das bedeutet, dass die Wahrscheinlichkeit, bei dem Lottospiel 6 aus 49 zu gewinnen, nur 1/13.983.816 und somit weniger als ein Zehnmillionstel beträgt.
Höhere Ableitungen von Potenzfunktionen
Das Bilden von höheren Ableitungen einer Potenzfunktion mit führt auf Fakultäten: Wiederholtes Anwenden der Potenzregel liefert
Durch Erweitern mit erhält man für die -te Ableitung von die Formel
- ,
die den Spezialfall enthält.
Taylorsche Reihen und Eulersche Zahl
Eine prominente Gleichung, in welcher die Fakultäten vorkommen, ist die Formel für die Taylorreihe einer glatten Funktion mit Entwicklungspunkt :
Die Exponentialfunktion hat die einfachste aller Taylorreihen mit Fakultäten in Abhängigkeit vom Index im Nenner des Summanden:
Insbesondere ist die Eulersche Zahl die Summe der Kehrwerte der Fakultäten
und ihr Kehrwert die alternierende Summe desselben Musters:
Numerische Berechnung und Näherung
Rekursive und iterative Berechnung
Der numerische Wert für kann gut rekursiv oder iterativ berechnet werden, falls nicht zu groß ist.
Die größte Fakultät, die von den meisten handelsüblichen Taschenrechnern berechnet werden kann, ist da außerhalb des üblicherweise verfügbaren Zahlenbereiches liegt. Die größte als Gleitkommazahl im Format double precision des IEEE-754-Standards darstellbare Fakultät ist .
Programm in Python
Mit Bibliotheken für sehr große Ganzzahlen (keine Limitierung auf 32, 64 oder z. B. 512 Bit) benötigt zum Beispiel ein Chip des Typs AMD Ryzen 3900X @4GHz für die Berechnung von 10.000! mit 64-bit-Code 2,22 ms und mit 32-bit-Code 9,26 ms.[4]
Die Dezimaldarstellung der Zahl beginnt mit 284625968, hat insgesamt 35660 Stellen, wobei die letzten 2499 Stellen nur aus der Ziffer 0 bestehen.
# Syntax: Python 3.7
n = int(input('Fakultät von n = '))
f = 1
for i in range(1, n + 1):
f *= i
print(f'{n}! = {f}')
Unter Nutzung von Endrekursion sieht das Programm so aus:
def fak(n: int) -> int:
return 1 if n <= 1 else n * fak(n - 1)
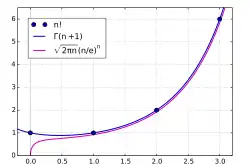
Näherung mit der Stirling-Formel
Für große liefert die Stirling-Formel eine gute Näherung für :
Dabei bedeutet , dass der Quotient aus linker und rechter Seite für gegen konvergiert.
Berechnung großer Fakultäten in C++, Excel
Viele Programmiersprachen haben die Funktion
Die Namen sind
lgamma→ C/C++/Python/Rgammaln→ MATLAB/Octave/SciPy/Excelloggamma→ JuliaLogGamma→ MathematicaGamma.logGamma→ Java
Damit kann die Fakultät sehr großer Zahlen (dann mit fallender Genauigkeit der Mantisse) berechnen.
- Beispiel
Ganzzahlanteil (ergibt den Exponenten) und Rest (ergibt den Logarithmus der Mantisse) voneinander trennen:
Fakultät-ähnliche Funktionen
Es gibt eine Reihe weiterer Folgen und Funktionen, die in ihrer Definition oder ihren Eigenschaften ähnlich aussehen wie die Fakultät:
Gammafunktion

Die Gammafunktion verallgemeinert die Fakultät und ist eine stetige Fortsetzung ihres Definitionsbereichs von den natürlichen hin zu den komplexen Zahlen:[5]
- für und
- Für kann die Gammafunktion folgendermaßen erweitert werden:[6]
Steigende und fallende Faktorielle
Eine kombinatorische Verallgemeinerung stellen die steigenden und fallenden Faktoriellen und dar, denn .
Primorial (Primfakultät)
| n | n! | n# | !n | n!! |
|---|---|---|---|---|
| 1 | 1 | 1 | 0 | 1 |
| 2 | 2 | 2 | 1 | 2 |
| 3 | 6 | 6 | 2 | 3 |
| 4 | 24 | 6 | 9 | 8 |
| 5 | 120 | 30 | 44 | 15 |
| 6 | 720 | 30 | 265 | 48 |
| 7 | 5040 | 210 | 1854 | 105 |
| 8 | 40320 | 210 | 14833 | 384 |
Die Primfakultät einer Zahl ist das Produkt der Primzahlen kleiner oder gleich der Zahl:
Subfakultät
Die vor allem in der Kombinatorik auftretende Subfakultät
bezeichnet die Anzahl aller fixpunktfreien Permutationen von Elementen.
Doppelfakultät
Definition
Die seltener verwendete Doppelfakultät oder doppelte Fakultät ist für gerade das Produkt aller geraden Zahlen kleiner gleich . Für ungerade ist es das Produkt aller ungeraden Zahlen kleiner gleich :[7]
Oft werden anstelle der Doppelfakultät Ausdrücke mit der gewöhnlichen Fakultät verwendet. Es gilt:
Werden nicht-ganzzahlige Funktionswerte zugelassen, dann gibt es genau eine Erweiterung auf negative ungerade Zahlen, sodass für alle ungeraden ganzen Zahlen gilt. Man erhält die Formel für ungerade .
Die Werte der Doppelfakultäten bilden die Folge A006882 in OEIS.
Beispiele
Anwendungsbeispiele
- Die Anzahl der -stelligen Kombinationen aus elementfremden Paaren gebildet aus Elementen wird gegeben durch die Rekursion mit Rekursionsanfang (2 Elemente!). Auflösung der Rekursion ergibt . Sollen z. B. Mannschaften durch Verlosung paarweise aufeinandertreffen, dann ist die Wahrscheinlichkeit, dass dabei zwei bestimmte gegeneinander spielen, gegeben durch .
- Die Anzahl der Elemente der Hyperoktaedergruppe ist .
- Die Anzahl der fixpunktfreien involutorischen Permutationen von Elementen ist .
- Das -te Moment der Standardnormalverteilung ist .
- Für natürliche gilt .
Multifakultät
Analog zur doppelten Fakultät wird eine dreifache (), vierfache (), …, -fache Fakultät () rekursiv definiert:[8]
Weitere verwandte Funktionen
Primzahlexponenten
Falls nicht die vollständige Zahl gesucht ist, sondern nur der Exponent einer ihrer Primfaktoren, lässt sich dieser direkt und effizient ermitteln.
Hier steht für den Exponenten von in der Primfaktorzerlegung von .[9]
Im obigen Beispiel wäre für die Anzahl der Nullen am Ende von 10.000! der Exponent der 5 zu bestimmen, der Exponent der 2 ist auf jeden Fall größer.
Literatur
- Jacques Dutka: The Early History of the Factorial Function. Archive for History of Exact Sciences 43(3), 1991, S. 225–249.
- Leonhard Euler: Remarques sur un beau rapport entre les séries des puissances tant directes que réciproques. (1749), in Histoire de l’Académie Royale des Sciences et Belles-Lettres 17 (1761), 1768, S. 96/97 (französisch).
- Leonhard Euler: Evolutio formulae integralis integratione a valore x=0 ad x=1 extensa. 4. Juli 1771, in Novi commentarii academiae scientiarum imperialis Petropolitanae 16, 1772, S. 121 (lateinisch).
- Adrien-Marie Legendre: Recherches sur diverses sortes d’intégrales définies. (13. November 1809), in Mémoires de la classe des sciences mathématiques et physiques de l’Institut de France 10, 1809, S. 485 (französisch).
- Hermann Kinkelin: Ueber eine mit der Gammafunction verwandte Transcendente und deren Anwendung auf die Integralrechnung. (Juli 1856), in: Journal für die reine und angewandte Mathematik 57, 1860, S. 122–138 (beim GDZ: digizeitschriften.de).
- J. W. L. Glaisher: On the Product 1¹.2².3³...nⁿ. In: The Messenger of Mathematics 7, 1878, S. 43–47 (englisch); Textarchiv – Internet Archive.
Weblinks
- Peter Luschny: The Homepage of Factorial Algorithms. Effiziente Algorithmen und weitere Informationen (englisch).
- Eric W. Weisstein: Factorial. In: MathWorld (englisch).
Einzelnachweise
- ↑ Factorial. In: MacTutor History of Mathematics archive. Universität St. Andrews, abgerufen am 6. August 2024 (englisch).
- ↑ Ilja Nikolajewitsch Bronstein, Konstantin Adolfowitsch Semendjajew: Taschenbuch der Mathematik. 5. Auflage. Verlag Harri Deutsch, 2001, ISBN 3-8171-2005-2, S. 13.
- ↑ Tilo Arens, Frank Hettlich, Christian Karpfinger, Ulrich Kockelkorn, Klaus Lichtenegger, Hellmuth Stachel: Mathematik. 5. Auflage. Springer, Berlin 2023, ISBN 978-3-662-64388-4, S. 77.
- ↑ Microsoft Visual Studio 2022, Quick-&-Dirty-Programm, C++, klassische Langzahl-Multiplikation unter Nutzung von umul128/emulu und addcarry_u64/u32, ohne weitere Optimierungen. Abschätzungen ergeben eine Laufzeit von 70...80 ms für einen Pentium 4/2.8 und 20...25 ms für einen AMD Athlon XP 2800+.
- ↑ Leonhard Euler: De progressionibus transcendentibus, seu quarum termini generales algebraice dari nequeunt. (28. November 1729), Commentarii academiae scientiarum imperialis Petropolitanae 5, 1738, S. 36–57 (lateinisch).
- ↑ E. Freitag, R. Busam: Funktionentheorie. Springer-Verlag, ISBN 3-540-31764-3, S. 225.
- ↑ Eric W. Weisstein: Double Factorial. In: MathWorld (englisch).
- ↑ Eric W. Weisstein: Multifactorial. In: MathWorld (englisch).
- ↑ Donald Knuth: The Art of Computer Programming. 3. Auflage. Volume 1: Fundamental Algorithms. Addison-Wesley, 1997, ISBN 0-201-89683-4, S. 47–48 (englisch).