Discorsi e dimostrazioni matematiche

Discorsi e dimostrazioni matematiche intorno a due nuove scienze attenenti alla meccanica e i movimenti locali (deutsch Unterredungen und mathematische Demonstrationen über zwei neue Wissenszweige, die Mechanik und die Fallgesetze betreffend, kurz Discorsi) ist das letzte Werk von Galileo Galilei, das er 1638 als wissenschaftliches Testament über seine Erkenntnisse zur Physik veröffentlichte, insbesondere zur Mechanik (Statik) und zu den Fallgesetzen (Dynamik) als „neue Wissenschaften“. Es ist teilweise auf Italienisch und teilweise auf Latein verfasst.

Nach seinem Dialogo sopra i due massimi sistemi del mondo (Dialogo) hatte 1633 die römische Inquisition die Veröffentlichung aller existierenden und zukünftigen Werke Galileis verboten (siehe Reaktion der Inquisition). Nach dem Scheitern seiner anfänglichen Versuche, die Discorsi in Frankreich, Deutschland und Polen zu veröffentlichen, wurde es von Louis Elsevier im niederländischen Leiden gedruckt und herausgegeben, wo der Erlass der Inquisition keine Wirkung entfaltete. Fra Fulgenzio Micanzio, der offizielle Theologe der Republik Venedig, hatte Galilei zunächst angeboten, ihn zu unterstützen, wies aber darauf hin, dass ihn die Veröffentlichung der Discorsi in Venedig in unnötige Schwierigkeiten bringen könnte. Galilei erlitt keinen Schaden durch die Inquisition, als das Buch im Januar 1639 die römischen Buchhandlungen erreichte und alle verfügbaren Exemplare (etwa fünfzig) schnell verkauft wurden.^[1]

Galilei widmete Discorsi dem Gesandten des Königs von Frankreich beim Heiligen Stuhl, François de Noailles (1584–1644), der Papst Urban VIII. nach dem Inquisitionsverfahren von 1633 mehrfach bat, seine Strafe (Hausarrest) zu mildern. Er fühlte sich „verwirrt und niedergeschlagen wegen der Misserfolge meiner anderen Arbeiten“ und hatte beschlossen, seine „Studien handschriftlich an einem Ort niederzulegen, der vielen Fachkennern zugänglich wäre“. Dabei fiel seine Wahl auf de Noailles.

Er verfasste die Discorsi in einem ähnlichen Stil wie Dialogo, in dem drei Männer (Simplicio, Sagredo und Salviati) über verschiedene Fragen diskutieren, die Galilei als „Akademiker“^{[A 1]} zu beantworten versucht. Es gibt jedoch eine bemerkenswerte Veränderung bei den Männern; vor allem Simplicio argumentiert nicht mehr ganz so einfältig und stur aristotelisch, wie sein Name vermuten lässt. Seine Argumente entsprechen Galileis frühen Überzeugungen, während Sagredo seine mittlere Schaffensperiode repräsentiert und Salviati als sein engster Vertrauter Galileis neueste Theorien vertritt.

Das Buch ist in vier Tage unterteilt, die jeweils verschiedene Bereiche der Physik behandeln.^[2]

Am ersten Tag behandelt Galilei Themen, die in der Physik und in der Mechanik der aristotelischen Schule diskutiert wurden. Er bietet auch eine Einführung in die beiden neuen Wissenschaften. Die Ähnlichkeit zwischen den diskutierten Themen, den gestellten Fragen sowie der Stil und die Quellen geben Galilei die Struktur für seinen ersten Tag. Am ersten Tag werden die Sprecher des Unterredung vorgestellt: Salviati, Sagredo und Simplicio, die gleichen wie im Dialogo. Am zweiten Tag behandelt er die Frage der Festigkeit von Materialien.

Der dritte und vierte Tag befassen sich mit der Wissenschaft der Bewegung. Am dritten Tag geht es um gleichförmige und natürlich beschleunigte Bewegungen, wobei die Frage der Endgeschwindigkeit bereits am ersten Tag behandelt wurde. Der vierte Tag befasst sich mit der Wurfparabel, einer zusammengesetzten Bewegung. Die gleichförmige Bewegung wird als Bewegung definiert, die über beliebige gleiche Zeitintervalle die jeweils gleiche Strecke zurücklegt. Die Quantifizierung beliebig führt die Gleichförmigkeit ein und drückt sie expliziter aus als frühere Definitionen.^[2]

Galilei hatte einen weiteren Tag über den Stoß begonnen, konnte ihn aber nicht zu seiner eigenen Zufriedenheit abzuschließen. Auf diesen Abschnitt wurde in den ersten vier Tagen der Diskussion häufig Bezug genommen. Er erschien schließlich in der Ausgabe von Galileis Werken von 1718^[3] und wird oft als „Sechster Tag“ zitiert entsprechend der Nummerierung in der Ausgabe von 1898.^[4] Während dieses zusätzlichen Tages wurde Simplicio durch Aproino, einen ehemaligen Schüler Galileis in Padua, ersetzt.

Sagredo versteht nicht, warum bei manchen Maschinen im Kleinen gelingt, was im Großen nicht bestehen kann, warum sich die mechanischen Eigenschaften von geometrischen Formen abhängig von ihrer Größe ändern. Salviati sagt, diese allgemeine Meinung sei falsch. Die Dimension spiele eine Rolle: Ein Pferd, das aus einer Höhe von 3 oder 4 Ellen (2,15 m) fällt, bricht sich die Knochen, während eine Katze, die aus mehr als der doppelten Höhe fällt, dies ohne Verletzung übersteht, ebenso wie eine Grille, die von einem Turm fällt. Man sehe dies auch an den Proportionen der Äste einer alten Eiche gegenüber dem jungen Baum. Das erste Beispiel für Festigkeit ist ein verdrilltes Hanfseil, das aus kurzen Fasern besteht, die sich unter Zugkraft komprimieren und sich wie ein Seil um eine Winde zu etwas viel Stärkerem verbinden.^[5]

Es schließt die Frage an, welche Kräfte den inneren Zusammenhalt der „Fasern“ eines Stoffes verursachen. Vakuum verhindert, dass sich zwei plattpolierte Platten voneinander trennen, obwohl sie sich leicht gegeneinander verschieben lassen. Dies gibt Anlass zu einem Experiment, mit dem geprüft werden soll, ob sich Wasser dehnen lässt oder ob ein Vakuum entsteht. Sagredo hatte beobachtet, dass eine Saugpumpe Wasser nicht mehr als 18 Ellen (9,7 m) hochheben kann. Salviati stellt fest, dass das Gewicht dieser Wassersäule den Widerstand gegen das Vakuum darstellt.^{[A 2]} Auch ein Seil oder ein Eisenstab würde durch das eigene Gewicht bei Überschreiten einer spezifischen Länge reißen. Mit einem Analogieschluss aus einem Versuch mit einem bis zum Bruch belasteten Kupferstab berechnet er die Reißlänge des Kupferdrahts auf 4.800 Ellen (2.600 m).^{[A 3]} Es stellt sich die Frage, ob winzige Hohlräume im Inneren des Metalls existieren oder ob es eine andere Erklärung für die charakteristische Reißfestigkeit (bzw. Kohäsion) gibt. Gold, das durch Hitze verflüssigt wird, erreicht nach der Abkühlung wieder die vorherige Festigkeit – es bleibt unklar, wie der Effekt zustande kommt.^[6]

Die nächste Diskussion führt am Beispiel von abrollenden (abgewälzten) Polygonen mit unterschiedlicher Größe um einen gemeinsamen Mittelpunkt zur Betrachtung der Menge der Teilstrecken mit Berührungen und leeren Zwischenräumen. Im Grenzfall des Kreises, einem Polygon mit unendlich vielen Ecken, führt dies zu einem „Gedankenlabyrinth“ über Unendlichkeiten, das Unteilbare und das Kontinuum. Nach Galilei/Salviati entstehen Schwierigkeiten, weil „wir mit unserem endlichen Intellekt das Unendliche diskutieren, indem wir ihm Eigenschaften zusprechen, die wir an dem Endlichen, Begrenzten kennen. Das geht aber nicht an, denn die Attribute des Großseins, der Kleinheit und Gleichheit kommen dem Unendlichen nicht zu. […] Die Attribute ‚groß‘, ‚klein‘, ‚gleich‘ gelten weder zwischen unendlichen [Mengen] noch zwischen Unendlichem und Endlichem.“ Er zeigt dies mit der These, dass die Anzahl der Quadratzahlen gleich der Anzahl der Quadratwurzeln ist und man dabei auf einen Widerspruch stößt. Bei solchen Reihen würde man erwarten, dass eine einzige unendliche Zahl die „Einheit“ bildet. Salviati demonstriert dann, dass eine gerade Linie der Grenzfall eines unendlich großen Kreises ist, eine „Metamorphose beim Übergang vom Endlichen zum Unendlichen“.^[7]

Die Runde diskutiert Eigenschaften des Unteilbaren bei allerfeinsten Pulvern in unendlich kleine Atome (infiniti suoi atomi) sowie dem Unterschied von Feststoffen (Gold, Silber, Blei) zu Flüssigkeiten (Wasser oder Säuren, geschmolzene Metalle). Die mit einem Hohlspiegel aus Sonnenlicht erzeugte Hitze führt zu einer Diskussion, wie die konzentrierte Kraft der Sonne Metalle schmelzen kann. Salviati folgert, dass Licht eine Bewegung bzw. Geschwindigkeit haben muss und beschreibt einen (erfolglosen) Versuch, dessen Geschwindigkeit zu messen.^{[A 4]} Im weiteren Verlauf geht es um Verdichtung und Verdünnung von Materie sowie der Existenz des Vakuums.^[8]

Aristoteles/Simplicio glaubt, dass Körper mit einer Geschwindigkeit fallen, die proportional zum Gewicht ist, und bestreitet, dass Bewegung in einem Vakuum möglich sei. Salviati bezweifelt, dass Aristoteles dies jemals überprüft hat, und führt seine Ansichten mit vielen Beispielen ad absurdum, darunter die unterschiedliche Sinkgeschwindigkeit von Gold oder Blei in Wasser oder Quecksilber aufgrund unterschiedlicher Dichte und Auftriebskraft. Er leitet die Möglichkeit ab, wie bestimmte Stoffe im Wasser abhängig von Wassertemperatur (Prinzip des Galileo-Thermometer)^{[A 5]} oder Salzgehalt auftauchen oder untergehen.^{[A 6]} Beim Fallen durch die Luft sind der Luftwiderstand und die Form des Körpers zu berücksichtigen. Ein Stück Blattgold (die dichteste aller Substanzen) schwebt langsam durch die Luft, eine mit Luft gefüllte Blase fällt viel langsamer als Blei. Ebenholz fällt es nur wenig langsamer als Blei, das zehnmal so viel wiegt. Salviati glaubt, dass in einem Medium ohne Widerstand (im Vakuum) alle Körper – eine Wollflocke oder ein Stück Blei – mit der gleichen Geschwindigkeit fallen würden. Salviati beschreibt Galileis Verfahren zur Messung des Gewichts der Luft,^{[A 7]} das einen Faktor 1:400^{[A 8]} im Vergleich zu Wasser ergab.^[9]

Die Messung der Fallgeschwindigkeit ist wegen der kleinen Zeitintervalle schwierig. Er nimmt an, dass beim freien Fall nach einer Beschleunigung eine konstante Geschwindigkeit erreicht wird, in dem sich Luftwiderstand und Anziehungskraft der Erde die Waage halten. Galilei nutzte Pendel gleicher Länge mit Blei- oder Korkgewichten. Die Schwingungsdauer, die proportional zur Quadratwurzel der Länge ist, bleibt gleich, auch wenn er den Korken weiter auslenkt, um auszugleichen, dass er wegen des geringeren Gewichts früher zum Stillstand kommt.^{[A 9]} Dies führt zu einer Diskussion über die Schwingung der Saiten einer Zither oder eines Klaviers (cimbalo), die zueinander in Resonanz geraten. Sie finden heraus, dass nicht nur die Länge der Saite für die Tonhöhe wichtig ist, sondern auch die Spannung und die Stärke der Saite (z- B. einer Metall- oder einer Darmsaite). Mittels der Anregung von Wasserwellen kann man herausfinden, dass die Oktave die Schwingungsanzahl verdoppelt. Neben Konsonanzen (Quarte, Quinte) gibt es Dissonanzen (Sekunde, in der nur jede neunte Schwingung zusammentrifft).^[10]

Ausgehend vom Hebelgesetz des Archimedes beweist Salviati, dass eine Waage nicht nur mit gleichen Armen, sondern auch mit ungleichen Armen mit Gewichten verwendet werden kann, die umgekehrt proportional zu den Abständen vom Drehpunkt sind. Anschließend zeigt er, dass das Moment eines Gewichts, das an einem einseitig gelagerten Balken hängt, proportional zum Quadrat der Länge ist. Er demonstriert, dass die Bruchfestigkeit von Trägern verschiedener Breiten und Dicken, die an einem oder beiden Enden abgestützt sind, mit dem Kubus der Dicke zunimmt. Wenn man Länge und Dicke in gleichem Verhältnis vermehrt, bleiben Festigkeit und Widerstandskraft gegen das Zerbrechen und Verbiegen aufgrund des höheren Eigengewichts nicht unverändert.^[11]

Salviati zeigt, dass dies auch für Schiffe, Paläste und die Natur gilt. Tierknochen für größere Tiere müssen überproportional größer sein. Ein kleiner Hund könne zwei oder drei Hunde auf seinem Rücken tragen, während ein Pferd kaum ein anderes Pferd zu tragen vermöge. Er beweist, dass ein Stab, der über das Knie gelegt wird, am ehesten in der Mitte bricht, und zeigt, wie weit ein größeres Gewicht entlang eines Balkens platziert werden kann, ohne dass er bricht. Er weist nach, dass die optimale (d. h. leichteste) Form für einen Balken, der an einem Ende verankert ist und am anderen Ende eine Last trägt, parabelförmig ist. Er zeigt auch, dass Hohlzylinder stärker sind als massive Zylinder mit demselben Gewicht, so wie es die Natur bei den Knochen der Vögel und bei Strohhalmen geschaffen hat. Er beruft sich auf den Mathematiker Luca Valerio (1553–1618) als „größten Geometer und Archimedes unserer Zeit“.^[12]

Ab dem dritten Tag verfasste Galilei die Discorsi teilweise formal wie ein Lehrbuch und beschrieb die Axiome, Lehrsätze und Hilfssätze in Latein, während die Unterhaltung weiterhin auf Italienisch geführt wird. Dazu stellte Galilei 20 Aufgaben (problemi) zur Anwendung der Erkenntnisse.

Salviati definiert zunächst die gleichförmige Bewegung und zeigt die Beziehung zwischen Geschwindigkeit, Zeit und zurückgelegtem Weg. Anschließend definiert er die gleichmäßig beschleunigte Bewegung, bei der die Geschwindigkeit pro Zeiteinheit um denselben Betrag zunimmt. Fallende Körper beginnen sehr langsam, und er zeigt, dass ihre Geschwindigkeit^{[A 10]} proportional zur Zeit zunimmt und die zurückgelegte Strecke proportional zum Quadrat der Zeit ist. Salviati beschreibt ein Experiment, bei dem eine glatt polierte Messingkugel durch eine mit glattem Pergament beklebte Rinne in einem 12 Ellen langen (etwa 6,5 m) langen Holzbrett als schiefen Ebene gerollt wurde.^{[A 11]} Dieser Vorgang wurde für verschiedene Neigungen und Streckenabstände vielfach wiederholt, wobei die Zeiten durch genaues Wiegen der Wassermenge gemessen wurden, die aus einem dünnen Kanal in einem Strahl vom Boden eines großen Eimers austrat. Auf diese Weise konnte Salviati/Galilei die gleichmäßig beschleunigte Bewegung nachweisen. Er beschreibt die Messung der Kraft, die eine Kugel auf der schiefen Ebene antreibt (siehe Torricelli-Prinzip). Er führt die Begriffe Gleichgewicht (von Kräften), Moment (Geschwindigkeit), Impuls (l'impeto), Energie (l’energia) bzw. Tendenz zum Fall (il momento del descendere) ein. Wenn längs einer geneigten Ebene, sowie längs der Senkrechten gleicher Höhe ein und derselbe Körper sich aus der Ruhelage bewegt, so verhalten sich die beiden Fallzeiten zueinander wie die Länge der geneigten Ebene zur Länge der Senkrechten (Theorem III).^[13]

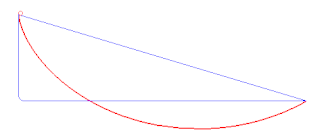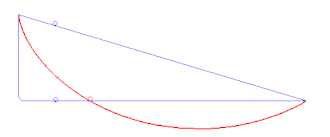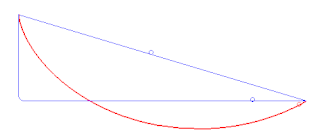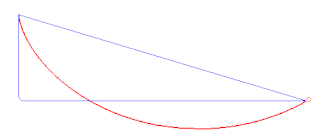
Als Nächstes betrachtet Salviati den Fall entlang der Sehnen vom höchsten Punkt eines Kreises und zeigt, dass die Zeit die gleiche ist wie die für den vertikalen Fall vom Scheitelpunkt zum tiefsten Punkt des Kreises (Theorem VI). Dann führt er verschiedene zusammengesetzte Bewegungen auf verschiedenen schiefen Ebenen auf. Er sucht den schnellsten Weg (Brachistochrone)^{[A 12]} zwischen den Endpunkten einer schiefen Ebene und glaubt irrtümlich, dass der Kreisbogen die schnellste Bahn ist (Theorem XXII).^[14]

Die Bewegung von Geschossen besteht aus einer Zusammensetzung von gleichmäßiger horizontaler Bewegung und einer natürlich beschleunigten vertikalen Bewegung, die eine Flugbahn entsprechend einer Halbparabel ergeben (Theoreme I bis III). Zwei Bewegungen, die im rechten Winkel zueinander stehen, können mit Hilfe der Summe der Quadrate addiert werden. Er zeigt detailliert, wie die Parabeln unter verschiedenen Bedingungen zu konstruieren sind.^[15]

Der Luftwiderstand zeigt sich auf zweierlei Weise: Er wirkt stärker auf Körper mit geringerer Dichte und bietet schnelleren Körpern größeren Widerstand. Eine Bleikugel wird etwas schneller fallen als eine Eichenkugel, aber der Unterschied ist vernachlässigbar. Die Geschwindigkeit nimmt jedoch nicht unbegrenzt zu, sondern erreicht ein Maximum. Bei kleinen Geschwindigkeiten ist die Wirkung des Luftwiderstands gering, sie ist größer, wenn man eine aus eine mit „übernatürlicher Geschwindigkeit“ abgefeuerte Flinten- oder Kanonenkugel betrachtet. Dies kann dazu führen, dass das Geschoss nach dem Verlassen des Laufs langsamer wird.^[16]

Die Wirksamkeit (Galilei spricht von Kraft und Energie) eines Geschosses ist nicht allein von seiner eigenen Geschwindigkeit abhängig, sondern ebenso von der Geschwindigkeit des Ziels, z. B. bei einem Fliehenden. Die Wirkung ist geringer, wenn sich das Ziel frei bewegen und ausweichen kann, weniger hart ist oder schräg getroffen wird. Die Impulsgröße am Ende der Parabel ist in Richtung der Tangente am größten. Die Wurfweite einer Kanonenkugel ist am größten, wenn sie in der Neigung von einem halben rechten Winkel (also 45°) abgefeuert wird. Galilei gibt Tabellen für die Höhe und die Entfernung (Amplitude) in Abhängigkeit vom Abschusswinkel (Anstieg) an. Die horizontale Geschwindigkeit entspricht dabei derjenigen, die dem freien Fall aus einer bestimmten Höhe (Galilei nennt sie „Sublimität“ (sublimita)) entspricht.^[17]

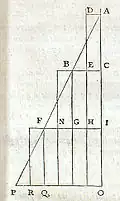
Ein gespanntes Seil oder eine Kette ist niemals horizontal gerade, sondern nähert sich einer Parabel an.^{[A 13]} Salviati erläutert dies an einem Seil, das mit schweren Gewichten c und d an beiden Enden gespannt ist (siehe Zeichnung). Falls es kein eigenes Gewicht hätte, wäre es horizontal geradlinig gespannt. Beim Anhängen eines noch so kleinen Gewichts h in der Mitte (c) wird das Seil nachgeben bis zum Punkt f. So wie das verschiebliche Laufgewicht am langen Arm einer Schnellwaage beim Ausbalancieren einen größeren Weg (im Verhältnis der beiden Hebel) als das Wägegut zurücklegt, so muss das Absinken des Gewichts h durch ein entsprechendes Anhaben der Gewichte c und d kompensiert werden.^{[A 14]} Diese Verhältnisse werden durch die Skizze im darunterliegenden Kreis verdeutlicht.^[18]

In der Ausgabe von Galileis Werken von 1718 wurden dem Werk frühere Betrachtungen Galileis über den Schwerpunkt von Körpern hinzugefügt. Dies betrifft den Schwerpunkt von Körpern an einem Waagebalken, einem parabolischen Konoid mit eingeschriebenen und umschriebenen Zylindern sowie einem abgestumpften Zylinder oder Kegel.^[19]

Der fünfte Tag der Discorsi findet „nach einer Pause von einigen“ Jahren statt. Es werden Zweifel diskutiert über die Definition der gleichförmigen Bewegung als „Methode des gleichen Vielfachen“, ausgehend von Erörterungen der Proportionalität in Euklids Elementen (Buch 5) und in Archimedes' Über Spiralen. Die Galilei-Definition des Verhältnisses eignet sich besser zur Beschreibung der Messung einer physikalischen Größe als eine feste Maßeinheit, in Galileis Worten: „Indem man also die Quantitäten oder die Werte der einfachen Verhältnisse multipliziert, erhält man die Quantität oder den Wert des Verhältnisses, welches man aus jenen zusammengesetzt nennt.“^[20]

Simplicio, der „sich in einigen Beweisen zu diversen Bewegungsproblemen und in der Lehre vom Schwerpunkt nicht hat zurecht finden können“, wird durch Paolo Aproino, einen ehemaligen Schüler Galileis in Padua, ersetzt. Am Beispiel des Hammers wird erörtert, wie die „Geschwindigkeit eines geringfügigen Körpers die Kraft eines bedeutenden Widerstandes überwindet und eine geringe Bewegung erzeugt“. Dazu ersann Galilei eine Messvorrichtung, indem er Wasser durch ein Loch aus einem oberen in einen unteren Eimer fließen ließ. Vor Versuchsbeginn waren die beiden Eimer in Balance mit einem Gegengewicht. Als der Stopfen aus dem Loch gezogen wurde, wurde die Seite der beiden Eimer zunächst leichter und näherte sich dann wieder genau dem ursprünglichen Gleichgewicht. Sagredo erklärt dieses Ergebnis damit, dass die Stoßwirkung des Wassers genau der Menge (d. h. Gewicht) des Wasserstrahls zwischen den beiden Eimern entspricht, da dieser weder auf den oberen noch auf den unteren Eimer eine Schwerkraft ausübt.^[21]

Beim Rammen mit einem Bären fällt ein schwerer Hammerkopf auf einen Pfahl. Mit jedem Stoß rammt er den Pfahl um eine gewisse Strecke weiter in den Boden, oft abnehmend mit der Tiefe des Eindringens. Ein einfach aufgelegtes (sehr großes) Gewicht entfaltet jedoch nicht die gleiche Wirkung. Jeder Stoß einer aus der Höhe herabfallenden Masse leistet Arbeit (lavora). Diese Energie (energia) ergibt sich aus dem Gewicht (peso) des Hammers und des Pfahls sowie durch ihre (relativen) Geschwindigkeiten.^{[A 15]} In einem Gedankenexperiment hängen sie einen auf dem Boden stehenden Körper über eine Umlenkrolle an ein Seil. An diesem lassen sie ein ebenso schweres Gewicht aus einer Höhe von zwei Ellen fallen. Salviati folgert, dass sich im Gleichgewichtszustand der beschleunigte Körper und abgebremste Gewicht mit gleichförmiger Geschwindigkeit bewegen.^{[A 16]} Beim Fall eines kleineren Gewicht beruft sich Galilei auf den Impuls und demonstriert das Kräftegleichgewicht an einer schiefen Ebene.^[22]

Salviati betrachtet das Schlagen eines Hammers aus Blei auf einen Amboss (Verformung), das verhinderte Eintreiben eines Nagels in sehr hartes Holz, das Springen eines Balls oder eines Schlagstocks auf einer straff gespannten Membran (elastischer Stoß) sowie das Auspressen von Öl (Druck). Ein Einfluss (d. h. Bewegung) auf den geschlagenen (gestoßenen) Körper sei notwendig, um eine Wirkung zu erzielen. Diese Übertragung brauche Zeit. Er beendet den Tag mit einem Beispiel: „Ein biegsamer aber langer Bogen einer Armbrust trägt viel weiter als ein harter von geringer Zugweite, weil jener längere Zeit hindurch das Geschoss begleitet und demselben allmählich die Kraft mitteilt, während dieser alsbald dasselbe entsendet.“^[23]

Viele zeitgenössische Wissenschaftler, wie z. B. Pierre Gassendi, bestritten die Methodik, mit der Galilei sein Fallgesetz konzipierte. Zwei der Hauptargumente sind, dass seine Erkenntnistheorie dem Beispiel des platonischen Denkens oder des Hypothetico-Deduktivismus folgte. Sie wurde nun als ex suppositione betrachtet, d. h. das Wissen um das Wie und Warum von Wirkungen vergangener Ereignisse, um die Voraussetzungen für die Erzeugung ähnlicher Wirkungen in der Zukunft zu bestimmen. Die galileische Methodik entsprach der aristotelischen und archimedischen Erkenntnistheorie. Als Antwort auf einen Brief von Kardinal Bellarmin im Jahr 1615 unterschied Galilei seine Argumente und die von Kopernikus als natürliche Annahmen im Gegensatz zu den „fiktiven“, die „nur um der astronomischen Berechnungen willen eingeführt werden“, wie die Hypothese von Ptolemäus über Exzentrik und Äquanten.^[24]

Galileis frühe Schriften gelten als seine ersten Versuche, Vorlesungsnotizen für seinen Kurs „Hypothese der Himmelsbewegungen“ zu verfassen, während er an der Universität Padua lehrte. Diese Notizen spiegelten die Meinungen seiner Zeitgenossen am Collegio wider und enthielten einen „aristotelischen Kontext mit dezidiert thomistischen Obertönen“.^[25] Es wird angenommen, dass diese früheren Arbeiten ihn ermutigten, Demonstrationen anzuwenden, um seine Entdeckungen zur Bewegung zu beweisen.

Seine Experimentiermethoden wurden durch die Aufzeichnungen und Nachbildungen von Wissenschaftlern wie James MacLachlan, Stillman Drake, R.H. Taylor und anderen belegt. Somit bildete er sich seine Ideen nicht nur ein, wie der Historiker Alexandre Koyré behauptete, sondern suchte sie mathematisch zu beweisen.

Die beiden im Titel genannten Wissenschaften sind Mechanik (Festigkeit von Materialien) und Fallgesetze (Bewegung von Objekten), also die Vorläufer der modernen Materialwissenschaft und Kinetik.^[26] Im Titel des Buches sind „Mechanik“ und „Bewegung“ getrennt, da zu Galileis Zeiten „Mechanik“ nur Statik und Festigkeit von Materialien bedeutete.^[27] Sie beschreiben Galileis Auseinandersetzung mit der aristotelischen Physik.

Discorsi beginnt mit einer Demonstration der Gründe dafür, dass eine große Struktur, die genau so proportioniert ist wie eine kleinere, notwendigerweise schwächer sein muss, bekannt als das Quadrat-Würfel-Gesetz. Im Verlauf der Diskussion wird dieses Prinzip auf die erforderliche Dicke der Knochen eines großen Tieres angewandt, möglicherweise das erste quantitative Ergebnis zur Biologie, das J. B. S. Haldanes Werk „On Being the Right Size, and Other Essays“ vorwegnimmt.^[28] Mit seinen Überlegungen wurde Galilei einer der Begründer der Kontinuumsmechanik.

Galilei ermittelte als erster Wissenschaftler die konstante Beschleunigung eines fallenden Körpers, indem er eine glattpolierte Kugel auf einer schiefen Ebene rollen ließ und die Zeit mit einer genauen Wasseruhr maß.

Während Aristoteles lehrte, dass schwere Körper schneller als leichte fallen, bewies Galilei, dass die Ursache nicht die größere Krafteinwirkung auf schwere Körper ist, sondern Gegenkräfte durch Luftwiderstand oder Reibung. Um diese Kräfte zu kompensieren, führte er Experimente mit einer schwach geneigten Rampe aus. Er polierte diese Rampe so, dass die Reibung möglichst minimal war, und ließ glattpolierte Kugeln mit unterschiedlichen Gewichten herunterrollen. Auf diese Weise bewies er empirisch, dass Materie unabhängig von der Masse durch den Einfluss der Schwerkraft senkrecht mit einem konstanten Faktor beschleunigt wurde.^[29]

Das in Folio 116V gefundene, aber nicht berichtete Experiment prüfte die konstante Beschleunigung fallender Körper aufgrund der Schwerkraft.^[30] Dabei wurde ein Ball aus festgelegten Höhen auf eine Ablenkplatte fallen gelassen, um seine Bewegung von der Vertikalen in die Horizontale umzuleiten. Die Daten des Experiments auf der schiefen Ebene wurden zur Berechnung der erwarteten Horizontalbewegung verwendet. Allerdings wurden in den Ergebnissen Unstimmigkeiten festgestellt: Die beobachteten horizontalen Entfernungen stimmten nicht mit den berechneten Entfernungen überein, die bei konstanter Beschleunigung zu erwarten waren. Galilei führte diese Unstimmigkeiten auf den Luftwiderstand und auf die Reibung zurück. Sie zwangen Galilei zu der Feststellung, das Postulat gelte nur unter „idealen Bedingungen“, d. h. in Abwesenheit von Reibung und/oder Luftwiderstand.

Die aristotelische Physik argumentierte, dass sich die Erde nicht bewegen dürfe, da der Mensch die Auswirkungen dieser Bewegung nicht wahrnehmen könne.^[31] Eine beliebte Begründung hierfür ist das Experiment mit einem Bogenschützen, der einen Pfeil senkrecht in die Luft schießt. Würde sich die Erde bewegen, so argumentierte Aristoteles, müsste der Pfeil an einer anderen Stelle als dem Abschusspunkt landen. Galilei widerlegte dieses Argument in seinem Dialog über die beiden hauptsächlichsten Weltsysteme. Er nannte das Beispiel eines Schiffes auf See. Das Schiff ist offensichtlich in Bewegung, aber die Seeleute können diese Bewegung nicht wahrnehmen. Würde ein Seemann ein schweres Objekt vom Mast fallen lassen, würde dieses Objekt (aufgrund der Vorwärtsbewegung des Schiffs) auf die Basis des Mastes fallen und nicht dahinter. Dies war das Ergebnis der gleichzeitigen horizontalen und vertikalen Bewegung von Schiff, Seeleuten und Objekt.

In einem seiner Gedankenexperimente mit fallenden Körpern beschrieb Galilei die Relativität von Bewegungen. Er erklärte, dass unter den richtigen Umständen „eine Bewegung eine andere überlagern kann, ohne dass sich dies auf die andere auswirkt [...]“. In Discorsi begründete Galilei dieses Argument, das zur Grundlage von Newtons erstem Gesetz, dem Trägheitsgesetz, wurde. Die eine ist die beschleunigte vertikale Bewegung aufgrund der Schwerkraft, die andere ist die gleichförmige horizontale Bewegung aufgrund des fahrenden Schiffes, die aufgrund des Trägheitsprinzips weiterhin die Flugbahn des Objekts beeinflusst. Die Kombination dieser beiden Bewegungen ergibt eine parabelförmige Kurve. Der Beobachter kann diese Parabel nicht erkennen, da Ball und Beobachter die horizontale Bewegung auf dem Schiff gemeinsam ausführen und somit nur die senkrechte, vertikale Bewegung wahrnehmbar ist. Erstaunlicherweise hatte niemand diese Theorie mit den einfachen Experimenten getestet, die nötig gewesen wären, um ein schlüssiges Ergebnis zu erhalten, bis Pierre Gassendi die Ergebnisse dieser Experimente in seinen Briefen mit dem Titel De Motu Impresso a Motore Translato (1642) veröffentlichte.^[31]

Das Buch enthält am ersten Tag eine Diskussion über die Unendlichkeit. Galilei betrachtet das Beispiel der Zahlen und ihrer Quadrate. Er beginnt mit der Feststellung:

Es lässt sich nicht leugnen, dass es genauso viele Quadratzahlen wie Zahlen gibt, da jede Zahl eine Quadratwurzel einer Quadratzahl ist:

1 ↔ 1, 2 ↔ 4, 3 ↔ 9, 4 ↔ 16 usw.

Doch er stellt einen offensichtlichen Widerspruch fest:

Wir haben jedoch eingangs gesagt, dass es viel mehr Zahlen als Quadratzahlen gibt, da der Großteil davon keine Quadratzahlen sind. Und nicht nur das: Die proportionale Anzahl der Quadratzahlen nimmt mit zunehmenden Zahlen ab.^{[A 17]}

Er löst den Widerspruch, indem er die Möglichkeit des Vergleichs unendlicher Zahlen (und des Vergleichs unendlicher und endlicher Zahlen) verneint:

Wir können nur schlussfolgern, dass die Gesamtheit aller Zahlen unendlich ist, dass die Zahl der Quadrate unendlich ist und dass die Zahl ihrer Wurzeln unendlich ist. Weder ist die Zahl der Quadrate kleiner als die Gesamtheit aller Zahlen, noch ist letztere größer als erstere; und schließlich sind die Attribute „gleich“, „größer“ und „kleiner“ nicht auf unendliche, sondern nur auf endliche Mengen anwendbar.

Diese Schlussfolgerung, dass die Größenzuordnung unendlicher Mengen aufgrund der widersprüchlichen Ergebnisse dieser beiden scheinbar natürlichen Vorgehensweisen als unmöglich gilt, stellt eine Lösung des Problems dar, die zwar mit den Methoden der modernen Mathematik vereinbar, aber weniger leistungsfähig ist. Die Lösung des Problems lässt sich verallgemeinern, indem man Galileis erste Definition betrachtet, was es bedeutet, wenn Mengen gleich groß sind, nämlich die Möglichkeit, sie eins zu eins abzubilden. Dies führt zu einer Methode, die Größen unendlicher Mengen zu vergleichen, die frei von Widersprüchen ist.

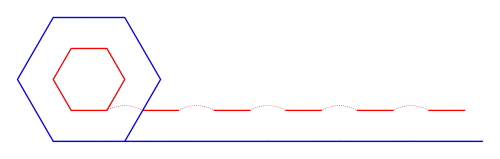
Diese Fragen zur Unendlichkeit ergeben sich aus Problemen mit rollenden Kreisen (siehe Rad des Aristoteles). Rollen zwei konzentrische Kreise mit unterschiedlichen Radien entlang von parallelen Geraden, so ist es klar, dass der kleinere gleiten muss, wenn der größere nicht gleitet. Galilei versucht, die Angelegenheit zu klären, indem er zunächst Sechsecke betrachtet und diese dann auf rollende 100.000-Ecke bzw. n-Ecke erweitert. Dabei zeigt er, dass auf der inneren Form eine endliche Anzahl endlicher Gleitbewegungen auftritt. Daraus schließt er: „Die Linie, die der größere Kreis beschreibt, besteht aus unendlich vielen Punkten, die sie vollständig ausfüllen; während die Linie, die der kleinere Kreis beschreibt, aus unendlich vielen Punkten besteht, die leere Räume hinterlassen und die Linie nur teilweise ausfüllen.“ Diese Erklärung würde heute nicht mehr als zufriedenstellend gelten.^{[A 18]}

Galileis Prinzipien wurden von seinem Assistenten und Nachfolger Evangelista Torricelli in der Abhandlung Opere geometriche von 1644 weiterentwickelt.^[32][33]

Der Theologe und Naturwissenschaftler Pierre Gassendi verteidigte 1645 Galileis Ansichten in seinem Buch De Motu Impresso a Motore Translato (Über die Bewegung, die von einem sich bewegenden Beweger ausgeht). Howard Jones schreibt in Gassendis Verteidigung für Galilei: Die Politik der Diskretion, Gassendi habe Verständnis für Galileis Argumente gezeigt und ihre Auswirkungen auf die physikalischen Einwände gegen die Erdbewegung klar erkannt.

Isaac Newton wies 1687 in Philosophiae Naturalis Principia Mathematica darauf hin, dass die ersten beiden von ihm entdeckten Gesetze aus Galileis Experimenten und Theorien über die Bewegung fallender Körper (senkrecht und auf einer schiefen Ebene) und über die Bewegung in zwei Dimensionen (Flugbahn eines Geschosses) abgeleitet sind.^[34][35]

In Frankreich beschrieb Pierre de Varignon, der bedeutendste Mathematiker unter König Ludwig XIV., 1725 in seinem Traité du mouvement et de la mesure des eaux jaillissantes (Abhandlung von der Bewegung und Messung des sprudelnden Wassers) detailliert den Theoremen und Beweisen aus Galileis Discorsi.^[36] In Frankreich erfolgten weitere Anerkennungen durch die Physiker und Mathematiker Joseph-Louis Lagrange in Mécanique Analytique (1788)^[37] und Pierre-Simon Laplace in Exposition du système du monde (1796)^[38] sowie durch den Ingenieur Claude-Louis Navier in Résumé des leçons données à l’École des ponts et chaussées sur l’application de la mécanique à l’établissement des constructions et des machines (Zusammenfassung der Lektionen an der École des ponts et chaussées über die Anwendung der Mechanik bei der Erstellung von Bauwerken und Maschinen).^[39]

In Deutschland wies der Physiker Leonhard Euler, Direktor der Akademien der Wissenschaften in Berlin und St. Petersburg, 1736 im Vorwort zu seinem Hauptwerk Mechanica sive motus scientia analytice exposita (Mechanik oder die Wissenschaft der Bewegung analytisch dargelegt) auf die großen Verdienste Galileis hin.^[40]

Der Mathematiker Guglielmo Libri (1803–1869) schrieb mit Blick auf die Verurteilung durch die Inquisition:

Die Galilei-Transformation ist die einfachste Koordinatentransformation, mit der physikalische Aussagen von einem Bezugssystem in ein anderes umgerechnet werden können.

Die Galilei-Zahl ist eine nach Galilei benannte dimensionslose Kennzahl aus dem Bereich der Strömungslehre.^[41]

Die Physiker Albert Einstein und Stephen Hawking legten unterschiedliche Maßstäbe an Galileis Wirken an:

Ein Teil von Discorsi war reine Mathematik, wie der Mathematiker Alfréd Rényi (1921–1970) hervorhob, der es das bedeutendste Buch über Mathematik seit über 2000 Jahren nannte: Die griechische Mathematik befasste sich nicht mit Bewegung, und so wurden in ihr nie mathematische Bewegungsgesetze formuliert, obwohl Archimedes die Differenzierung und Integration entwickelte. Discorsi ebneten den Weg für die mathematische Behandlung der Physik, indem sie Bewegung erstmals mathematisch behandelten. Der griechische Mathematiker Zenon hatte seine Paradoxien entwickelt, um zu beweisen, dass Bewegung nicht mathematisch behandelt werden kann und dass jeder Versuch, dies zu tun, zu Paradoxien führen würde, wie er u. a. am Beispiel von Achilles und die Schildkröte ausführte.^{[A 19]} Aristoteles bekräftigte diese Überzeugung, indem er behauptete, die Mathematik könne sich nur mit abstrakten und unveränderlichen Objekten befassen. Galilei verwendete genau die Methoden der Griechen, um zu zeigen, dass Bewegung sehr wohl mathematisch behandelt werden kann. Seine Idee war, die Paradoxie des Unendlichen von Zenons Paradoxien zu trennen. Er tat dies in mehreren Schritten. Zunächst zeigte er, dass die unendliche Folge S der Quadrate 1, 4, 9, 16, … genauso viele Elemente enthält wie die Folge N aller positiven ganzen Zahlen (unendlich). Dies wird heute als Galileis Paradoxon bezeichnet. Dann zeigte er mithilfe der griechischen Geometrie, dass ein kurzes Linienintervall genauso viele Punkte enthält wie ein längeres Intervall. Irgendwann formulierte er das allgemeine Prinzip, dass eine kleinere unendliche Menge genauso viele Punkte haben kann wie eine größere unendliche Menge, die sie enthält. Damit war klar, dass Zenons Bewegungsparadoxien ausschließlich aus diesem paradoxen Verhalten unendlicher Mengen resultierten. Rényi sagte, nachdem er dieses 2000 Jahre alte Hindernis aus dem Weg geräumt hatte, fuhr Galilei fort, seine mathematischen Bewegungsgesetze einzuführen und damit Newton vorwegzunehmen.^[42]

Das Fallgesetz wurde 1638 von Galilei veröffentlicht. Im 20. Jahrhundert stellten jedoch einige Experten die Richtigkeit von Galileis Experimenten infrage. Insbesondere der französische Wissenschaftshistoriker Alexandre Koyré begründet seine Zweifel damit, dass die in Discorsi beschriebenen Experimente zur Bestimmung des Fallgesetzes genaue Zeitmessungen erforderten, die mit der Technologie des Jahres 1600 nicht realisierbar erschienen. Laut Koyré wurde das Gesetz deduktiv entwickelt, und es seien lediglich illustrative Gedankenexperimente. Spätere Forschungen bestätigten die Experimente jedoch. Die Experimente an fallenden Körpern (genauer gesagt rollenden Kugeln) wurden mit den von Galilei beschriebenen Methoden reproduziert,^[43] und die Präzision der Ergebnisse stimmte mit Galileis Bericht überein. Spätere Untersuchungen von Galileis unveröffentlichten Arbeitspapieren aus dem Jahr 1604 zeigten deutlich die Realität der Experimente und die konkreten Ergebnisse, die zum Fallgesetz führten.^[44]

Der Physiker Max von Laue nannte Discorsi das „erste Lehrbuch der neuzeitlichen Physik“.^[45]

• Il Saggiatore (Galilei, 1623)
• Galileo (Raumsonde), 1989 gestartet zur Erforschung des Planeten Jupiter
• Galileo (Satellitennavigation), europäisches Navigationssatellitensystem
• Galileo Wissenswelt, Interaktive Museen auf den Inseln Fehmarn und Rügen
• Museo Galileo, Museum für Wissenschaftsgeschichte in Florenz

• Galileo Galilei: Discorsi e dimostrazioni matematiche intorno a due nuove scienze attinenti la meccanica e i movimenti locali. Elsevier, Leiden 3. Juni 1638 (italienisch, Latein, archive.org [PDF; 28,5 MB; abgerufen am 14. Juni 2025] erste vier Tage und Anhang). 
• Galileo Galilei, Discorsi e dimostrazioni matematiche intorno a due nuove scienze attinenti la meccanica e i movimenti locali (pag.664, of Claudio Pierini) publication Cierre, Simeoni Arti Grafiche, Verona, 2011, ISBN 978-88-95351-04-9.
• Galileo Galilei: Unterredungen und mathematische Demonstrationen über zwei neue Wissenszweige, die Mechanik und die Fallgesetze betreffend (Dritter und Vierter Tag). Wilhelm Engelmann, Leipzig 1891 (148 S., archive.org [PDF; 4,8 MB; abgerufen am 5. Juni 2025] Latein, italienisch: Discorsi e dimostrazioni matematiche intorno a due nuove scienze. Leiden 1638. Übersetzt von Arthur von Oettingen). 
• Galileo Galilei: Unterredungen und mathematische Demonstrationen über zwei neue Wissenszweige, die Mechanik und die Fallgesetze betreffend. Europa-Lehrmittel, 2007, ISBN 978-3-8085-5722-8 (404 S., Latein, italienisch: Discorsi e dimostrazioni matematiche intorno a due nuove scienze. Leiden 1638. Übersetzt von Arthur von Oettingen, Erstausgabe: Wilhelm Engelmann, Leipzig 1891, herausgegeben in drei Bänden Ostwalds Klassiker der exakten Wissenschaften). 

• Band 1 (Erster und zweiter Tag), Nr. 11, Engelmann, Leipzig 1890 (147 Seiten). Online: archive.org.
• Band 2 (Dritter und vierter Tag), Nr. 24, Engelmann, Leipzig 1891¹ (148 Seiten). Online: archive.org
• Band 3 (Fünfter und sechster Tag. Anhang zum dritten und vierten Tag), Nr. 25, Leipzig 1891² (70 Seiten). Online: archive.org.

Auszüge der Discorsi in der deutschen Übersetzung von Arthur von Oettingen sind enthalten in Anna Mudry, Galileo Galilei, Band 1.

In der Reihenfolge ihrer Veröffentlichung:

• William Wallace, A. Galileo and Reasoning Ex Suppositione: The Methodology of the Two New Sciences. PSA: Proceedings of the Biennial Meeting of the Philosophy of Science Association, Vol. 1974, (1974), pp. 79–104
• Stillman Drake: Galileo At Work. University of Chicago Press, Chicago 1978, ISBN 978-0-226-16226-3 (englisch, archive.org). 
• Anna Mudry: Galileo Galilei. Schriften, Briefe, Dokumente. Ruetten & Loening, Berlin 1987, ISBN 3-352-00122-7 (2 Bände). 
• Howard Jones, Gassendi's Defense of Galileo: The Politics of Discretion, Medieval Renaissance Texts and Studies 58, 1988 (englisch).
• Stillman Drake: Galilei (= Meisterdenker). Herder, Freiburg 1999, ISBN 3-926642-38-6. 
• Stafano Salvia: 'Galileo's Machine': Late Notes on Free Fall, Projectile Motion, and the Force of Percussion (ca. 1638–1639). In: Physics in Perspective. 16. Jahrgang, Nr. 4, 2014, S. 440–460, doi:10.1007/s00016-014-0149-1, bibcode:2014PhP....16..440S (englisch). 
• Alessandro De Angelis: Discorsi e Dimostrazioni Matematiche di Galileo Galilei per il Lettore Moderno. Codice, Torino 2021, ISBN 978-88-7578-930-5 (italienisch, codiceedizioni.it). 
• Alessandro De Angelis: Galilei's Two New Sciences for Modern Readers. Springer Nature, Heidelberg 2021, ISBN 978-3-03071952-4 (englisch, springer.com).  Mit einem Vorwort von Ugo Amaldi and Telmo Pievani.

Wikisource: Dialogues Concerning Two New Sciences – Quellen und Volltexte (englisch)

• Alessandro De Angelis: Galilei's „Discorsi e Dimostrazine Matematiche“. Universität Padua, 2021, abgerufen am 15. Juni 2025 (englisch, Vorlesung mit Powerpoint-Präsentation). 
• Anna Sosnowski: Cantor. 2023, abgerufen am 13. Juni 2025 (zur Geschichte der Unendlichkeit und der Mengenlehre). 

1. ↑ Maurice A. Finocchiaro: The Trial of Galileo: Essential Documents. Hackett Publishing Company, 2014, ISBN 978-1-62466-132-7, S. 30 (englisch). 
2. ↑ ^{a b} Arkady Plotnitsky, David Reed: Discourse, Mathematics, Demonstration, and Science in Galilei's Discourses Concerning Two New Sciences. In: Configurations. 9. Jahrgang, Nr. 1, 1. Januar 2001, S. 37–64, doi:10.1353/con.2001.0007 (englisch). 
3. ↑ Opere di Galileo Galilei. Tartini e Franchi, Florenz, 1718 (italienisch, Latein). 
4. ↑ Antonio Favaro (Hrsg.): Le Opere di Galileo Galilei, vol. VIII. Edizione Nazionale, Florenz, 1898 (italienisch, Latein). 
5. ↑ Galilei, Band 1, S. 1–11
6. ↑ Galilei, Band 1, S. 11–20
7. ↑ Galilei, Band 1, S. 20–37
8. ↑ Galilei, Band 1, S. 37–56
9. ↑ Galilei, Band 1, S. 56–74
10. ↑ Galilei, Band 1, S. 74–93
11. ↑ Galilei, Band 1, S. 93–108
12. ↑ Galilei, Band 1, S. 108–125
13. ↑ Galilei, Band 2, S. 3–34
14. ↑ Galilei, Band 2, S. 34–80
15. ↑ Galilei, Band 2, S. 80–100
16. ↑ Galilei, Band 2, S. 86–91
17. ↑ Galilei, Band 2, S. 100–118
18. ↑ Galilei, Band 2, S. 118–122
19. ↑ Galilei, Band 3, S. 3–21
20. ↑ Galilei, Band 3, S. 22–36
21. ↑ Galilei, Band 3, S. 37–40
22. ↑ Galilei, Band 3, S. 40–55
23. ↑ Galilei, Band 3, S. 55–58
24. ↑ Jones Wallace: Psa 1974 (= Boston Studies in the Philosophy of Science. Band 1974). University of Chicago Press, Springer, Philosophy of Science Association, 1976, ISBN 978-90-277-0648-5, Galileo and Reasoning ex Suppositione: The Methodology of the two New Sciences, S. 79–104, doi:10.1007/978-94-010-1449-6_4, JSTOR:495799 (englisch). 
25. ↑ Jones Wallace: Psa 1974 (= Boston Studies in the Philosophy of Science. Band 1974). University of Chicago Press, Springer, Philosophy of Science Association, 1976, ISBN 978-90-277-0648-5, Galileo and Reasoning ex Suppositione: The Methodology of the two New Sciences, S. 79–104, doi:10.1007/978-94-010-1449-6_4, JSTOR:495799 (englisch). 
26. ↑ Tucker McElroy, A to Z of Mathematicians, Facts on File (Infobase Publishing), p. 109.
27. ↑ Simon Gindikin, Tales of Physicists and Mathematicians, Springer Science & Business Media, S. 43.
28. ↑ J. B. S. Haldane: On Being the Right Size. In: John Maynard Smith (Hrsg.): Harper's Magazine. März 1926, S. 424–427 (englisch, archive.org [PDF; 424 kB; abgerufen am 14. Juni 2025]). 
29. ↑ William Wallace: Galileo and Reasoning Ex Suppositione: The Methodology of the Two New Sciences, S. 92.
30. ↑ William Wallace: Galileo and Reasoning Ex Suppositione: The Methodology of the Two New Sciences, S. 96.
31. ↑ ^{a b} Howard Jones: Gassendi's Defence of Galileo: The Politics of Discretion. S. 221–234.
32. ↑ Evangelista Torricelli: Opere geometriche. Florenz 1644 (italienisch). 
33. ↑ Kapitel „Über die Bewegung natürlich fallender Körper“: Einleitung, Sätze 3, 4, 5, 7, 10, 12, 14 / Kapitel „Bewegung von Geschossen“: Einleitung, Sätze 3, 9, 20 / Kapitel „Über Tische“ / Kapitel „Über das Quadrat“
34. ↑ Isaac Newton: Philosophiae Naturalis Principia Mathematica. London 1689 (Latein). 
35. ↑ italienische Übersetzung UTET Turin 1965, herausgegeben von Alberto Pala – Bücher 1 und 2: „Motion of Bodies“, Seiten 129, 178, 386, 557
36. ↑ nach italienische Übersetzung: Bologna, Dalla Volpe 1736 (Abschnitt 1 – „Über gleichmäßige Bewegungen“, Seiten 15, 18–21 / Abschnitt 2 – „Über die Bewegung schwerer Körper“, Seiten 39, 41, 42, 45)
37. ↑ 3. Auflage, Paris 1853 mit Anmerkungen von J. Bertrand (1. Teil „Statik“: Abschnitt 1 „über die verschiedenen Prinzipien der Statik“, Seiten 8–9 / Abschnitt 6 „über die Prinzipien der Hydrostatik“, Seiten 170 / 2. Teil „Dynamik“: Abschnitt 1 „über die verschiedenen Prinzipien der Dynamik“, Seiten 207–209)
38. ↑ italienische Übersetzung UTET Turin 1965, herausgegeben von Orietta Cambursano – Buch 3: „Die Gesetze der Bewegung“, Seiten 474, 486, 598–600, 610–612, 615, 619, 621
39. ↑ 3. Auflage, Paris 1864 (Einleitung: „Historisches Kompendium der Forschung über den Widerstand und die Elastizität fester Körper“ – Teil 2 und 3: „Galileo“ / Teil 1 – Absatz 150: „Anmerkungen zur Theorie der Bruchfestigkeit, die von Galileo, Mariotte und Leibniz vorgeschlagen wurde“, Seiten 169–171)
40. ↑ Vorwort und historische Anmerkungen
41. ↑ Josef Kunes: Dimensionless Physical Quantities in Science and Engineering. Elsevier, 2012, ISBN 978-0-12-391458-3, S. 123 (eingeschränkte Vorschau in der Google-Buchsuche). 
42. ↑ Alfred Renyi, Dialogs on Mathematics, Holden-Day, San Francisco, 1967.
43. ↑ Thomas B. Settle: An Experiment in the History of Science. In: Science. 133. Jahrgang, Nr. 3445, 1961, S. 19–23, doi:10.1126/science.133.3445.19, PMID 17759858, bibcode:1961Sci...133...19S (englisch). 
44. ↑ Stillman Drake: Galileo's Discovery of the Law of Free Fall. In: Scientific American. 228. Jahrgang, Nr. 5, 1973, v. 228, #5, pp. 84–92, doi:10.1038/scientificamerican0573-84, bibcode:1973SciAm.228e..84D (englisch). 
45. ↑ 1956 in seiner Rede „Von Kopernikus zu Einstein“ in Lindau

1. ↑ Dies bezieht sich auf seine MItgliedschaft der Accademia dei Lincei.
2. ↑ Dies entspricht der physikalischen Realität. Jedoch wird sie heute durch den atmosphärischen Umgebungsdruck auf die Wassersäule erklärt, nicht durch die Kraft des Vakuums.
3. ↑ Für Kupfer werden heute je nach Behandlung ca. 1.700 m bis 4.000 m (nach Kaltumformung) angegeben (Zugfestigkeit Rm = 150 MPa, Dichte ρ = 8.960 kg/m³)
4. ↑ Die erste präzise Messung der Lichtgeschwindigkeit auf der Erde gelang erst 1849 durch Hippolyte Fizeau mit Hilfe der Zahnradmethode, die eine Idee Galileis aufgreift. Galilei wollte mit einem Lichtsignal über große Entfernung (Fernrohr!) die Antwortverzögerung eines Beobachters messen, konnte damit aber nur dessen Reaktionszeit bestimmen.
5. ↑ Thermometer, das aus einem Glaszylinder besteht und mit Flüssigkeit und Auftriebskörpern gefüllt ist.
6. ↑ Salviati beschreibt, wie er ein Wachsstück so mit Sand anreichert, dass es genauso schwer wie Wasser wird. Sagredo verweist auf Fische, die mit Hilfe ihrer Schwimmblase den Auftrieb kontrollieren.
7. ↑ Er füllte komprimierte Luft in eine Blase und maß das zusätzliche Gewicht. Die zusätzliche Luftmenge bestimmte Galilei mit der Messung des verdrängten Wassers beim Anstechen der Blase. (S. 71–74)
8. ↑ Tatsächlich beträgt die Luftdichte unter Normalatmosphäre (bei 25 °C) etwa 1/850 der Wasserdichte.
9. ↑ Galilei ignoriert, dass diese Konstanz nur für kleine Auslenkungen zutrifft.
10. ↑ Mit der stetig zunehmenden Geschwindigkeit der beschleunigten Bewegung hatte Galilei Darstellungsprobleme, da er sie gedanklich nicht auf infinitesimal kleine Zeitabschnitte zurückführen konnte. Er spricht von „Geschwindigkeitsgraden“, also einer Anzahl von Wegstrecken pro endlicher Zeiteinheit. Dazu gehört auch die aus moderner Sicht zweifelhafte Gleichsetzung von „Moment “oder „Stoß“, die in etwa dem Impuls (m × v) entspricht.
11. ↑ Galilei ließ die Rotationsträgheit bzw. -energie der Kugeln unberücksichtigt, was den Beweis nicht schmälert.
12. ↑ Die Brachistochrone hat die Form einer Zykloide, nicht eines Kreisbogens (erstmals berechnet von Johann I Bernoulli im Jahr 1696). Es gilt als Geburtsstunde der Variationsrechnung.
13. ↑ Dies ist nur annähernd korrekt für flaches Durchhängen. Den allgemeinen Fall beschreibt die Kettenlinie mit dem Cosinus hyperbolicus (cosh). Sie wurde erstmals 1691 durch Leibniz, Huygens and Johann Bernoulli berechnet.
14. ↑ Dies entspricht der schon von Galilei beschriebenen Energieerhaltung im Gleichgewicht der Waage. In der modernen Mechanik würde man das Kräfteparallelogramm anwenden und zum gleichen Ergebnis kommen.
15. ↑ Galileis Argumente lenken in die richtige Richtung, sind aber aufgrund noch unklarer Vorstellung über Massenträgheit und Energie (Gewicht × Fallhöhe) in der Schlussfolgerung nicht korrekt.
16. ↑ Der Fall ist hinsichtlich der dann erreichten gemeinsamen Endgeschwindigkeit nicht schlüssig dargestellt. Mit moderner Physik wäre sie über die Energieerhaltung (Umwandlung von potentieller in kinetische Energie) einfach ableitbar.
17. ↑ In der modernen Mathematik gibt es eine Bijektion zwischen der Menge der positiven ganzen Zahlen N und der Menge der Quadrate S, und S ist eine echte Teilmenge von N mit der Dichte Null.
18. ↑ Siehe z. B. Stick-Slip-Effekt als selbsterregte Reibschwingung, die u. a. auch zum Quietschen von Bremsen führt.
19. ↑ Er betrachtete dies als eine unvermeidliche Beschränkung der Mathematik.