De motu antiquiora

De motu antiquiora^[1] (deutsch Die älteren Schriften über die Bewegung), oder einfach De motu, ist Galileo Galileis frühes schriftliches Werk über die Bewegung (nicht zu verwechseln mit Newtons De motu corporum in gyrum, das ebenfalls die abgekürzte Bezeichnung De motu trägt). Es wurde größtenteils zwischen 1589 und 1592 geschrieben,^[2] aber erst 1890 vollständig veröffentlicht.^[3] De motu enthält Galileis Vorstellung über die Bewegung während seiner Zeit in Pisa vor seinem Umzug nach Padua (1592).

Aufgrund von Unsicherheiten in seinem Verständnis und seinen mathematischen Berechnungen ließ Galilei das Manuskript zu Lebzeiten unvollendet und unveröffentlicht. Es ist unklar, ob dieses Buch ursprünglich als Buch in Dialogform oder in einer konventionelleren Schreibweise konzipiert war. Galilei arbeitete viele Jahre daran und fertigte von jedem Abschnitt mehrere Kopien an. In seinem Werk ändert sich der Schreibstil von einem Dialog zwischen Lehrer und Schüler, die seine Ansichten diskutieren, zu einem Essay. Später integrierte Galilei ausgewählte Argumente und Beispiele aus De motu in seine nachfolgenden Werke Le Mecaniche, Discorso intorno alle cose che stanno in su l'acqua (Abhandlung über schwebende Körper) und Discorsi e dimostrazioni matematiche intorno a due nuove scienze (Unterredungen und mathematische Demonstrationen über zwei neue Wissenszweige).

In De motu weist Galilei Aristoteles’ Ansichten zur Physik der Bewegung durchgängig zurück, oft in spöttischem Ton. Er verwendet dazu Reductio-ad-absurdum-Argumente, die Aristoteles’ Annahmen zur Bewegung logisch zu absurden Schlussfolgerungen im Widerspruch zu Beobachtung oder dessen ursprünglichen Annahmen führen und somit beweisen, dass die Annahmen falsch sein müssen. Trotz seiner häufigen scharfen Kritik an Aristoteles’ Physik hält Galilei in De motu jedoch weiterhin an den klassischen Elementen als grundlegender Ursache der Bewegung fest, in der sich alle Materie zu ihrem jeweiligen natürlichen Platz im Universum bewegt.

Er schlägt außerdem eine alternative Bewegungstheorie vor. Diese geht davon aus, dass sich Bewegung nicht durch strömende Luft fortpflanzt (wie die Peripatetiker lehrten), sondern

• dass das wahre Gewicht eines Körpers nur im Vakuum gemessen werden kann,
• dass das Gewicht des Körpers in einem Medium (d. h. das scheinbare Gewicht) durch seinen Auftrieb verändert wird,
• dass das aus diesem Auftrieb resultierende Gewicht die natürliche Bewegung des Körpers verursacht,
• dass die Wurfbewegung (im Unterschied zur natürlichen Bewegung) das Ergebnis einer aufgezwungenen Kraft ist, die das Gewicht des Wurfkörpers verändert, und
• dass die aufgezwungene Kraft mit der Zeit nachlässt, ähnlich wie ein heißer Gegenstand wieder in seinen natürlichen Kältezustand zurückkehrt.

De motu enthält den ersten Hinweis auf Galileis Interesse am Pendel. Er stellt fest, dass schwerere Objekte länger schwingen als leichtere.^[4] Allerdings deutet er dieses Phänomen fälschlicherweise als Beweis dafür, dass die in einem bewegten Körper vorhandene Kraft bei leichteren Körpern schneller abnimmt als bei schwereren, und (noch) nicht, dass der Luftwiderstand bei leichteren Körpern eine größere Wirkung hat.

Es ist fraglich, wie originell Galileis Ideen in De motu sind. Einige der Ideen stammen aus der Antike, andere aus dem Mittelalter und von Galileis unmittelbaren Vorgängern in Italien.^[5] Die im Essay behandelten Themen waren größtenteils schon seit langem in akademischen Kreisen diskutiert worden. Obwohl Galileis Lösungen für einzelne Probleme im Allgemeinen keine originellen Entdeckungen darstellen, vermittelt das Werk als Ganzes dennoch einen deutlichen Eindruck von Originalität. Dies liegt an der zugrunde liegenden Einheitlichkeit der Konzeption, der geschickten Verknüpfung der Ideen, dem ständigen Rückgriff auf die Mathematik sowie der Klarheit der Argumentation und des Stils.^[6]

De motu war ursprünglich zur Veröffentlichung vorgesehen, wurde jedoch von Galilei schließlich in unvollständiger Form aufgegeben. Was heute noch übrig ist, umfasst einen ersten Essayentwurf über Bewegung, mehrere überarbeitete Teile des Essays, einen Dialog, eine Reihe von Themen und Thesen sowie eine Reihe fragmentarischer Gedanken und Notizen.^[7]

Teile des Manuskripts wurden erstmals 1854 in Band 11 von Eugenio Albèris Ausgabe der Werke Galileis veröffentlicht, die restlichen Teile 1883 von Antonio Favaro. Das Manuskript wurde später unter dem Titel De motu in Band I der Opere di Galileo Galilei veröffentlicht, die 1890 von Favaro herausgegeben wurden und bestimmte Manuskripte enthielt, die Galilei in lateinischer Sprache selbst verfasst hatte. Die erste englische Übersetzung des Essayteils von De motu in der Übersetzung von Israel E. Drabkin wurde 1960 unter dem Titel On Motion and On Mechanics veröffentlicht, zusammen mit Stillman Drakes Übersetzung von Galileis Le Mecaniche.^[3] Eine spätere englische Übersetzung von Raymond Fredette (um 2010) ist nur als Digitalausgabe verfügbar und enthält auch den Dialog.^[8]

Zahlreiche Historiker haben über die genauen Einflüsse und die Entwicklung der frühen Dynamik Galileis während seiner Zeit an der Universität Pisa diskutiert und darüber, ob seine frühen Konzepte der eingeprägten Kräfte direkt auf die mittelalterliche Impetustheorie des 14. Jahrhunderts zurückgehen.

Pierre Duhem schlug vor, dass Galileis Dynamik eine Fortsetzung der von Johannes Buridan und Nicole Oresme gelehrten Tradition sei, in deren Rahmen Galilei die Impetustheorie während seiner gesamten Karriere weiter perfektionierte und dabei möglicherweise von Giovanni Battista Benedetti beeinflusst wurde, dessen Dynamik allgemein als Anhänger der Impetusphysik beschrieben wird.^[9]

Alexandre Koyré bemerkte ebenfalls Benedettis potenziellen Einfluss auf Galilei, argumentierte jedoch im Gegensatz zu Duhem, dass Galileis Pisaner Dynamik ein Versuch war, eine kohärente mathematische Formulierung des mittelalterlichen Impetus nach dem Vorbild der Statik des Archimedes zu erreichen. Doch anstatt diese zu perfektionieren, wie Duhem vermutet, scheiterte Galilei letztlich, was ihn dazu veranlasste, die mittelalterliche Tradition aufzugeben und in seiner Tätigkeit an der Universität Padua neu zu beginnen.^[10]

Der Mediävist Ernest Moody wies darauf hin, dass Galileis Argumente, mit denen er Aristoteles’ Erklärung der Wurfbewegung zurückwies, genau dieselben waren wie die von Buridan und Albrecht von Sachsen und daher nicht originär waren. Moody argumentierte jedoch gegen Duhem und Koyré, dass Galileis frühe Dynamik nicht dem Impetus von Buridan nachempfunden war, sondern vielmehr auf der Dynamik von Ibn Baddscha (Avempace) aus dem 11. Jahrhundert basierte, die wiederum auf den Ideen von Johannes Philoponos von Alexandria aus dem 6. Jahrhundert beruhte. Moody vermutet, dass Galilei möglicherweise durch Benedetti von Baddschas Theorien erfahren hat, aber auch, dass er durch seinen Zeitgenossen Girolamo Borro von Baddscha erfahren hat, der über Averroes’ Kritik an Baddschas Argumenten gegen die aristotelische Physik schrieb. Darüber hinaus wurde Galilei auch von seinem älteren Kollegen in Pisa, Francesco Buonamici, beeinflusst, der das Problem der Wurfbewegung ebenfalls in seinem eigenen Werk De motu diskutierte und erwähnte, dass Philoponos der Begründer der Theorie der eingeprägten Kräfte sei. Moody vermutet, dass Buonamici mit der mittelalterlichen Tradition der Impetusphysik vertraut war, allerdings nur aus zweiter oder dritter Hand, insbesondere im Hinblick auf den Beitrag des 14. Jahrhunderts zur Mechanik. Dies veranlasste Koyré zur Annahme, dass Buonamicis Ansichten eine Annäherung an Buridans Impetustheorie darstellten und mit der Theorie der eingeprägten Kräfte von Philoponos, Petrus Johannis Olivi und Franz von Marchia übereinstimmten. Moody nennt auch die Arbeiten von Benedictus Pererius, Julius Caesar Scaliger und Jacopo Zabarella als mögliche Einflüsse.^[11][12]

Raymond Fredette wie auch Enrico Giusti bezweifelten Benedettis Einfluss, den Galilei vermutlich nicht einmal gelesen hatte. Wahrscheinlicher sei ein Einfluss von Jacopo Mazzoni, der während der Entstehung von De motu antiquiora an der Universität Pisa Philosophie lehrte und Galileis Mentor war. In seiner Lehre widersprach Mazzoni einigen Aussagen Benedettis.^[13]

Stillman Drake wies darauf hin, dass De motu allem überlegen war, was seine Kollegen bis dahin veröffentlicht hatten. Vermutlich hielt er es vom Druck zurück, weil „seine Schlüsse über die Geschwindigkeit auf schiefen Ebenen nicht exakt den tatsächlichen Ergebnissen der Experimente entsprachen“.^[14]

Moody behauptet, dass es nicht nur einen Entwicklungsunterschied, sondern auch einen Bedeutungsunterschied zwischen der Galileischen Kraft (virtus impressa) und dem Buridanischen Impetus gibt: Buridans Impetus war eine „dauerhafte Realität“ (res permanens), die für immer unvermindert bestehen bliebe, wenn sie nicht durch Luft und Schwerkraft behindert würde, ähnlich wie die moderne Behandlung des Impulses. Galileis Kräfte hingegen waren in erster Linie selbsterschöpfend und wurden zusätzlich durch den Luftwiderstand behindert.^[12] Dies bedeutete, dass die Erklärungen für die natürliche Beschleunigung radikal voneinander verschieden waren, da bei einem Objekt, das unbegrenzt in ein Vakuum fällt, der Buridanische Impetus und die Geschwindigkeit des Objekts für immer bis ins Unendliche zunehmen würden, während die Galileische Kraft schließlich asymptotisch auf Null abfallen würde, wenn sich das Objekt im Vakuum einer Endgeschwindigkeit nähert.

Eine weitere Unterscheidung wird hinsichtlich der Rotationsbewegung getroffen, insbesondere bei der Erklärung der Rotation der Himmelssphären. Frühere Philosophen wie Avicenna, al-Ghazālī, Moses Maimonides und die meisten christlichen Scholastiker dachten, dass die Rotation der Himmelssphären eine konstante Kraft erforderte, um ihre Rotation aufrechtzuerhalten. Sie identifizierten Aristoteles’ „Intelligenzen“, die diese Sphären antrieben, mit den Engeln der Offenbarung, wodurch sie jeder Sphäre einen Engel zuordneten.^[15] Buridan schlug vor, dass es für den Antrieb nicht notwendig sei, Engel oder „Intelligenzen“ als Beweger des Himmels anzunehmen. Wenn wir unterstellen, dass Gott bei der Erschaffung der Welt die Himmelskörper mit ihrer gegenwärtigen Rotationsgeschwindigkeit in Bewegung setzte, wäre kein weiteres Eingreifen eines „Bewegers“ erforderlich, weil ihr ursprünglicher Antrieb ohne Widerstand oder entgegengesetzte Kräfte für immer unvermindert bestehen bliebe. Galilei hingegen beantwortet diese Frage nur teilweise, indem er behauptet, die Rotation der Himmelssphären sei weder das Ergebnis einer erzwungenen Bewegung, da sich die Sphären nicht vom Zentrum des Universums entfernen, noch handele es sich um eine natürliche Bewegung, da sich Sphären scheinbar nicht einem natürlichen Ort nähern. Dies wirft die Frage auf, ob die Rotation der Sphären fortwährend fortschreitet oder ob sie ohne Krafteinwirkung irgendwann zum Stillstand kommen. Galilei lässt diese Frage unbeantwortet.

Der Dialog über Bewegung besteht aus einer Unterhaltung zwischen Alessandro (dem Lehrer) und Domenico (dem Schüler), der zunächst die Lehre des Aristoteles vertritt. Drabkin vertrat die Meinung, dass der Dialog über Bewegung vor dem Essay über Bewegung entstanden ist und dass ihn Galilei nicht vollendet hat.^[16] Die englische Übersetzung Dialogue on Motion between Alessandro and Domenico von Raymond Fredette, basierend auf Antonio Favoros Gesamtausgabe,^[17] liegt nur als digitaler Text vor.^[18]

Auf einer Wanderung in der Umgebung von Pisa stellt Domenico sechs Fragen,^[19] die aber nur teilweise diskutiert werden:

1. Ist am Wendepunkt der Bewegung eine Ruhepause erforderlich?
2. Wie fallen zwei Körper gleicher Größe aber unterschiedlicher Schwere (z. B. aus Holz und Eisen) durch die Luft, wenn sie gleichzeitig von einem bestimmten sehr hohen Ort herabgelassen werden?
3. Warum ist die natürliche Bewegung am Ende schneller ist als in der Mitte oder am Anfang, die erzwungene Bewegung jedoch am Anfang schneller als in der Mitte und dort schneller als am Ende?
4. Warum fällt derselbe Körper in der Luft schneller, als er im Wasser sinkt, und warum fallen bestimmte Körper in der Luft, tauchen aber im Wasser nicht unter?
5. Warum fliegen Kanonenkugeln und Bleikugeln weiter in einer geraden Linie, wenn sie im rechten Winkel zum Horizont abgefeuert werden, als wenn sie sie in einer Linie parallel zum Horizont abgefeuert werden, obwohl die erste Bewegung der natürlichen Bewegung mehr entgegensteht?
6. Warum schleudern dieselben Geschütze schwerere Kugeln schneller und weiter als leichtere, wie beispielsweise Eisenkugeln im Vergleich zu Holzkugeln, obwohl die leichteren der Antriebskraft weniger widerstehen?

Alessandro beschreibt zunächst die grundsätzliche Natur der Bewegung, die einen Beweger, Bewegliches und ein Medium erfordere. Am Beispiel einer rotierenden Marmorkugel widerlegt er Aristoteles, der die Aufrechterhaltung der Bewegung auf die Luft (als Medium) zurückführte, die sich vor dem Beweglichen spalte und am Ende wieder zusammenfüge und damit antreibe. Alessandro verweist darauf, dass die Flugbahn einer schräg abgeschossenen Kanonenkugel sei aus einer natürlichen und einer erzwungenen Bewegung zusammengesetzt. Das Medium unterstütze nicht, sondern wirke der Bewegung entgegen. Die bewegende Kraft einer erzwungenen Bewegung „bleibt uns verborgen“.^[20]

Dann weist Alessandro Aristoteles Behauptung in Über den Himmel „mit Verachtung“ zurück, dass die Erde das schwerste aller Dinge sei und das Feuer das leichteste. Aristoteles erkläre nicht, warum Quecksilber und Blei schwerer als Erde sind.^[21] Schwere und Leichtigkeit seien nur als relative Größen zueinander sinnvoll. Alessandro führt weitere Gedanken aus wie in Kapitel 8 (Auftrieb) und Kapitel 12 des Essays sowie seinen späteren Abhandlungen über schwimmende und sinkende Körper. Domenico hält dagegen, dass daher das Leichte schwerer als Luft sein müsse. Alessandro entgegnet: „O lächerliche Schimären! O ungeschickte Denkweisen der Menschen, die nicht nur der Wahrheit nicht nahe kommen, sondern ihr selbst entgegenstehen! Aber, Himmel! wie, frage ich dich, sollen wir den Schimären dieser Leute Glauben schenken, mit denen sie vorgeben, die verborgensten Geheimnisse der Natur zu erklären, wenn sie bei Dingen, die sozusagen völlig den Sinnen zugänglich sind, vorschnell das Gegenteil der Wahrheit behaupten?“^[22] Es folgt eine Aufzählung von praktischen Beispielen: Ein Kürbis falle in der Luft und schwimme auf dem Wasser, ein Fisch schwimme im Wasser und sei genauso schwer wie Wasser, ein Stein gehe unter, weil er schwerer ist als das Gewicht des verdrängten Wassers.^[23]

Alessandro antwortet auf die erste Frage wie in Kapitel 20 des Essays, dass am Wendepunkt kein Ruhezustand eintritt, und widerlegt Aristoteles ausführlich.^[24] Dann folgt ein Monolog zum Vakuum ähnlich zu Kapitel 10 des Essays.^[25] Analog zu Kapitel 7 diskutiert Alessandro dann die Schnelligkeit und Langsamkeit von Bewegungen, auch das Beispiel des aufgeblasenen Luftsacks im Wasser und in der Luft, und beklagt sich über das Diskussionsverhalten einer „großen Zahl neuerer Philosophen, die behaupten, Dinge zu wissen, die sie eher durch die Autorität anderer als durch Beweise wissen“. In die Enge getrieben, würden sie hinzufügen: „Eine solche Meinung ist schon früher mehr als ausreichend und vollständig widerlegt worden.“ Entsprechend Kapitel 8 argumentiert er, dass ein 100 Pfund schwerer Block aus Blei genauso schnell im Wasser sinke wie ein 10 Pfund schwerer Block. Dies gelte auch für den Fall in der Luft und im Vakuum.^[26]

Zur dritten Frage argumentiert Alessandro ähnlich wie in Kapitel 19, auch für den freien Fall mit zunehmender Geschwindigkeit. Die Beobachtung werde jedoch erschwert durch die verzerrte Sicht (vgl. Kapitel 22). Als weiteres Beispiel nennt er einen Taucher, der aus großer Höhe ins Wasser springt und bis zum Grund abgebremst wird.^[27] Sodann spricht er über das Abkühlen eines heißen Eisen, die nachlassende Geschwindigkeit eines Geschosses und der verschwindende Klang einer Glocke.^[28]

Galilei gliederte seinen Aufsatz in unnummerierte Kapitel; später fügte Drabkin nummerierte Kapitel hinzu, um Querverweise zu erleichtern.^[29] Der Leser sei darauf hingewiesen, dass Galileis Argumente zwar durchweg stichhaltig erscheinen, einige seiner Argumente jedoch aufgrund fehlerhafter Prämissen oder mathematischer Berechnungen Fehler enthalten.

Galilei beginnt mit der Definition von Schwere und Leichtigkeit, was dem modernen Konzept der relativen Dichte ähnlich ist. Zwei Substanzen gelten als gleich schwer, wenn sie sowohl bezüglich Volumen als auch Gewicht gleich groß sind. Eine Substanz wird als „schwerer“ bezeichnet als eine zweite, wenn sie bei gleichem Volumen mehr wiegt als die zweite.

In dieser gleichen Anordnung wird die zweite Substanz als „leichter“ als die erste bezeichnet. Galilei definiert „Leichtigkeit“ (levius) jedoch im Sinne von „weniger schwer“ (in gravitate minor) und damit anders als in einem relativen Sinn. Mit anderen Worten: Alle Dinge haben ein gewisses Maß an inhärenter Schwere und nicht eine inhärente Leichtigkeit. In späteren Überarbeitungen von De motu betont Galilei diesen Unterschied, indem er das Wort „leicht“ im gesamten Werk streicht und durch „weniger schwer“ ersetzt. So beginnt ein überarbeitetes zweites Kapitel mit: „Dass sich schwerere Körper naturgemäß näher am Zentrum befinden und weniger schwere weiter davon entfernt, und warum.“ Mit dieser Unterscheidung kann Galilei betonen, dass die Aufwärtsbewegung tatsächlich eine erzwungene Bewegung durch ein schwereres Medium und nicht durch die inhärente Leichtigkeit des Objekts ist.

Galilei geht von einer quasi-aristotelischen Ordnung des Universums aus, die auf der Vier-Elemente-Lehre beruht, in denen sich die Dinge entsprechend ihrem richtigen Platz bewegen: Die Erde befindet sich im Zentrum, Wasser befindet sich über der Erde, Luft über dem Wasser und Feuer über der Luft. Basierend auf dieser Ordnung scheint Galilei ein ptolemäisches System anzunehmen, das die Erde in den Mittelpunkt des Universums stellt, trotz seiner späteren Anerkennung von Nikolaus Kopernikus’ De revolutionibus orbium coelestium in Kapitel 20.

Galilei weist darauf hin, dass Aristoteles keinen anderen Grund für die Anordnung der vier Elemente nannte, als dass dies der göttlichen Vorsehung entspreche. Galilei hält diese Ansicht jedoch für unbefriedigend und glaubt, dass Aristoteles mit seiner Kritik an den antiken monistischen und atomistischen Theorien möglicherweise falsch lag. Er argumentiert, dass diese eine logische Erklärung für die Anordnung der Elemente liefern würde, falls die Monisten und Atomisten Recht hätten: Schwerere Körper würden mehr Teilchen dieser Materie auf engerem Raum einschließen und auch engere Stellen einnehmen, wie etwa jene in der Nähe des Zentrums des Universums (Gallei behauptet, dass Räume enger werden, wenn wir uns dem Zentrum einer Kugel nähern, ohne seine Bedeutung weiter zu erläutern). Beispielsweise nehmen Erdelemente wenig Raum ein, während Luftelemente viel Raum einnehmen. Galileo kommt zu dem Schluss, dass die Anordnung des Universums nicht zufällig gewählt ist, sondern mit Umsicht und Gerechtigkeit ausgeführt wurde.

Körper, die aus den klassischen Elementen bestehen, ruhen an ihrem vorgesehenen Platz. Werden sie jedoch über einen leichteren Körper geschoben, bewegen sie sich unter diesen, sofern der leichtere nicht gezwungen wird, unter dem schwereren zu bleiben. Für leichtere Körper gilt das Umgekehrte. Bei einer „natürlichen“ Bewegung (im Gegensatz zu einer „erzwungenen“ Aufwärtsbewegung) müssen sowohl die Schwere/Leichtigkeit des Körpers als auch die Schwere/Leichtigkeit des Mediums verglichen werden. Wäre Wasser nicht leichter als Stein, würde ein Stein im Wasser nicht versinken. Galilei betont erneut, dass Schwere/Leichtigkeit (d. h. Dichte) streng wie zuvor definiert zu betrachten sind, da nicht das Gewicht der gesamten Wassermasse berücksichtigt wird, sondern das Gewicht eines Teils des Wassers, dessen Volumen dem des Körpers entspricht, der das Wasser verdrängt. Bewegung resultiert dann aus der relativen Schwere zweier Körper, was Galilei in den folgenden Kapiteln zu beweisen versucht.

Der Beweis wird erbracht.

Nach diesem Beweis kommt Galilei zu dem Schluss, dass es offensichtlich ist, dass Körper, die schwerer als Wasser sind, zwangsläufig unter Wasser bleiben. Da Körper, die sich nach unten bewegen, zudem schwerer als das Medium sein müssen, kann man sagen, dass sich schwere Körper aufgrund ihres Gewichts nach unten bewegen.

Da natürliche Bewegung durch die Schwere/Leichtigkeit des Mediums und des Körpers entsteht und die jeweilige Schwere/Leichtigkeit durch entsprechende Gewichte gleichen Volumens verglichen werden kann, folgert Galilei, dass dasselbe auch für Gewichte auf einer Balkenwaage gilt, und dass, wenn man den Hebel als Analogie für Bewegung betrachtet, leicht verständlich wird, warum Festkörper, die leichter als Wasser sind (z. B. Holz), nicht vollständig in Wasser eingetaucht werden – der Schwerere kann nicht vom Schweren angehoben werden. Unter dieser Annahme kann die Ursache der Bewegung von Körpern, die sich natürlich (auf die gleiche Weise wie Gewichte an einer Balkenwaage) nach oben oder unten bewegen, allein auf das Gewicht zurückgeführt werden.

Durch diese Hebelanalogie bewegt sich ein bewegliches Objekt durch die „Druckwirkung“ des Mediums. Wenn Holz gewaltsam untergetaucht wird, schiebt das Wasser es wieder heraus, wenn es sich in Richtung seines eigentlichen Platzes bewegt. Auf die gleiche Weise wird ein Stein im freien Fall von seiner Position gestoßen und nach unten gedrückt, weil er schwerer ist als das Medium. Natürliche Bewegung kann daher als „erzwungen“ betrachtet werden.

Unterschiede in der Bewegungsgeschwindigkeit entstehen auf zwei Arten: Entweder bewegt sich derselbe Körper in unterschiedlichen Medien oder verschiedene Körper bewegen sich durch dasselbe Medium. Darüber hinaus lässt sich der freie Fall, in dem sich verschiedene Körper in unterschiedlichen Medien bewegen, auf diese beiden Arten vereinfachen. In beiden Fällen hängt die Bewegungsgeschwindigkeit von derselben Ursache ab: dem größeren oder geringeren Gewicht des Mediums und der bewegten Körper. In dieser Argumentation konzentriert sich Galilei auf die primäre Ursache der Bewegung und nicht auf „zufällige“ (z. B. die Form des Körpers) oder externe Ursachen.

Aristoteles behauptete, dass sich derselbe Körper in einem dünneren Medium schneller bewegt als in einem dichteren Medium, und dass daher die Ursache für die Langsamkeit der Bewegung die Dichte des Mediums und die Ursache für die Geschwindigkeit die Dünne des Mediums sei. Galilei weist jedoch darauf hin, dass Aristoteles diese Behauptung nur auf der Grundlage von Erfahrung aufstellte, z. B. die Beobachtung, dass sich ein bewegter Körper in Luft schneller bewegt als im Wasser. Diese Erklärung der Ursache für diese Wirkung sei unzureichend, da es viele bewegte Körper gibt, die sich in dichteren Medien von Natur aus schneller bewegen als in dünneren. So sinkt ein aufgeblasener Luftsack in der Luft langsam, steigt im Wasser jedoch schnell auf. Darüber hinaus stellt Galilei fest, dass sich bei einer Abwärtsbewegung eine schwerere Substanz schneller bewegt als eine leichtere und sich bei einer Aufwärtsbewegung die leichtere Substanz schneller bewegt.

Bewegt sich ein Körper in unterschiedlichen Medien, bewegt sich ein schwererer Körper in diesem Medium schneller als in einem leichteren Medium. Ein leichterer Körper bewegt sich in diesem Medium schneller als in einem leichteren Medium. Wenn wir also herausfinden, in welchem Medium ein bestimmter Körper schwerer ist, haben wir auch das Medium gefunden, in dem er schneller fällt. Und wenn wir herausfinden, wie viel schwerer derselbe Körper in einem Medium im Vergleich zu einem anderen ist, wissen wir, wie viel schneller er sich bewegt.

Galilei führt aus, dass sich zwei Körper in zweierlei Hinsicht unterscheiden können: 1) Sie bestehen aus demselben Material, haben aber unterschiedliche Größe (also Volumen), und 2) sie bestehen aus unterschiedlichem Material, aber a) unterscheiden sie sich in Größe und Gewicht, b) unterscheiden sich im Gewicht, aber nicht in der Größe, oder c) unterscheiden sich in Größe, aber nicht im Gewicht. Anschließend widerlegt er Aristoteles’ Behauptungen für jede Kombination.

Aristoteles behauptet, dass sich bei sich natürlich bewegenden Körpern aus demselben Material der größere schneller bewegt, so dass sich ein großes Stück Gold schneller bewegt als ein kleines Stück, und dass das Verhältnis ihrer Geschwindigkeiten dem Verhältnis ihrer Größen entspricht. Galilei behauptet, dies sei lächerlich, da dies bedeuten würde, dass bei zwei Bleikugeln, von denen eine hundertmal größer ist als die andere, die leichtere Kugel hundertmal länger beim Fall aus großer Höhe brauchen würde als die schwerere Kugel.

Stattdessen argumentiert Galilei, dass Objekte aus dem gleichen Material trotz unterschiedlicher Größe mit der gleichen Geschwindigkeit fallen, und dass jeder, der davon überrascht ist, auch überrascht sein wird, dass ein großes Stück Holz nicht weniger schnell schwimmt als ein kleines Stück Holz. In einem anderen Beispiel schlägt Galilei vor, ein Stück Wachs mit Sand zu vermischen, sodass es etwas schwerer als Wasser wird und langsam zu sinken beginnt. Beim Vergleich eines Stücks gemischten Wachses, das ein Hundertstel des zuerst betrachteten Wachses ausmacht, argumentiert Galilei, würde niemand glauben, dass das kleinere Stück Wachs hundertmal länger zum Sinken braucht. Dasselbe lässt sich über die Analogie mit den Gewichten auf einer Balkenwaage sagen: Wenn zwei große und gleich große Gewichte ausbalanciert sind und auf einer Seite ein winziges Gewicht hinzugefügt wird, wird die schwerere Seite sinken, aber sie wird nicht schneller sinken, als wenn die beiden Gewichte stattdessen kleine Gewichte wären. Ähnlich verhält es sich mit Wasser und Holz: Ein Gewicht auf der Waage stellt das Gewicht des Holzes dar und das andere Gewicht das Gewicht einer Wassermenge, die dem Volumen des Holzes entspricht. Wenn das Gewicht der Wassermenge dem Gewicht des Holzes entspricht, sinkt das Holz nicht. Macht man das Holz jedoch etwas schwerer, sodass es sinkt, sinkt es nicht schneller als ein kleines Stück desselben Holzes, das zunächst so viel wiegt wie eine ebenso kleine Wassermenge und dann etwas schwerer gemacht wird.

In einem anderen Argument nimmt Galileo an: Wenn es zwei Körper gibt und sich ein Körper von Natur aus schneller bewegt als der andere, dann wird sich eine Kombination aus beiden Körpern langsamer bewegen als der Körper, der sich allein schneller bewegt, und auch wird sich die Kombination schneller bewegen als der Körper, der sich allein langsamer bewegt. Beispiel: Eine Wachskugel und eine luftgefüllte Balse sind beide in Wasser getaucht und bewegen sich beide im Wasser nach oben, aber die luftgefüllte Blase bewegt sich schneller als das Wachs. Sind die beiden miteinander verbunden, steigt die Kombination langsamer als die Blase allein, aber schneller als das Wachs allein. Dasselbe lässt sich über nach unten fallende Körper sagen: Ist einer aus Holz und der andere aus einer Blase, fällt das Holz schneller als die Blase, sind sie jedoch verbunden, fallen sie zusammen mit einer mittleren Geschwindigkeit. Mit dieser Annahme kehrt Galilei dann zu Aristoteles’ Behauptung zurück, dass schwerere Körper aus demselben Material schneller fallen: Wenn zwei Körper aus demselben Material, aber unterschiedlicher Größe (und daher unterschiedlichen Gewichts) mit unterschiedlicher Geschwindigkeit fallen, dann würde dies dazu führen, dass die miteinander verbundenen Körper eine mittlere Geschwindigkeit haben, wenn sie miteinander verbunden werden. Allerdings wird das Gesamtgewicht der beiden Körper größer sein als das jedes einzelnen Körpers. Daher müsste laut Aristoteles das kombinierte Gewicht sogar noch schneller fallen als das jedes einzelnen Körpers, was zu einem Widerspruch führt. Der einzige Weg, diesen Widerspruch zu beheben, besteht darin, Aristoteles’ Behauptung zurückzuweisen und anzunehmen, dass die beiden Körper aus demselben Material, aber unterschiedlicher Größe (und Gewicht) mit der gleichen Geschwindigkeit fallen. Dasselbe Argument taucht erneut in Galileis Unterredungen und mathematische Demonstrationen über zwei neue Wissenszweige auf.

Galilei betrachtet dann die Geschwindigkeitsverhältnisse von Körpern aus unterschiedlichem Material, die sich im selben Medium bewegen. Diese Körper unterscheiden sich in dreierlei Hinsicht voneinander: entweder in der Größe, aber nicht im Gewicht, oder im Gewicht, aber nicht in der Größe, oder sowohl in Gewicht als auch Größe. Es muss jedoch nur der Fall der Körper betrachtet werden, die sich im Gewicht, aber nicht in der Größe unterscheiden, da sich die anderen Unterschiede auf diesen reduzieren lassen. Bei Körpern unterschiedlicher Größe, aber nicht im Gewicht, können wir vom größeren einen Teil nehmen, der gleich groß ist wie der kleinere; die Körper unterscheiden sich dann im Gewicht, aber nicht in der Größe. Und der größere Körper wird zum kleineren dasselbe Verhältnis beibehalten wie der vom größeren genommene Teil, da bewiesen wurde, dass sich Körper aus demselben Material trotz unterschiedlicher Größe mit der gleichen Geschwindigkeit bewegen. Bei Körpern unterschiedlicher Größe und Gewicht, wenn wir vom größeren einen Teil nehmen, der gleich groß ist wie der kleinere, haben wir ebenfalls zwei Körper unterschiedlichen Gewichts, aber nicht unterschiedlicher Größe. Und der Teil wird in seiner Bewegung mit dem kleineren dasselbe Verhältnis beibehalten, wie das Ganze mit dem größeren – und im Fall von Körpern aus demselben Material bewegen sich Teil und Ganzes mit der gleichen Geschwindigkeit.

Aristoteles behauptete, dass bei der Bewegung desselben Körpers in unterschiedlichen Medien das Verhältnis der Geschwindigkeiten gleich dem Verhältnis der Dichte der Medien sei. Galilei beweist, dass diese Annahme absurd und falsch ist. Wenn die Geschwindigkeiten im gleichen Verhältnis zur Dichte der Medien stehen, dann steht umgekehrt auch die Dichte der Medien im gleichen Verhältnis zu den Geschwindigkeiten. Da Holz in Luft, aber nicht in Wasser fällt und die Geschwindigkeit in Luft in keinem Verhältnis zur Geschwindigkeit im Wasser steht, steht die Dichte der Luft in keinem Verhältnis zur Dichte des Wassers – was absurd ist.

Galilei untersucht dann das Verhältnis der Geschwindigkeiten desselben Körpers, der sich während einer Aufwärtsbewegung in unterschiedlichen Medien bewegt. Wenn Feststoffe, die leichter als Wasser sind, vollständig in Wasser eingetaucht sind, werden sie mit einer Kraft nach oben getragen, die sich aus der Differenz zwischen dem Gewicht eines Wasservolumens entsprechend dem Volumen des eingetauchten Körpers und dem Gewicht des Körpers selbst ergibt. Galilei argumentiert, dass die natürliche Bewegung auf dem scheinbaren Gewicht eines Objekts beruht. Er schlussfolgert, dass wir, wenn wir die relativen Geschwindigkeiten desselben Körpers in zwei unterschiedlichen Medien berechnen wollen, von jedem Medium eine Menge nehmen, die dem Volumen des Körpers entspricht, und von den Gewichten jedes Mediums das Gewicht des Körpers abziehen. Die als Reste erhaltenen Zahlen verhalten sich zueinander wie die Geschwindigkeiten der beiden Medien. Ähnliche Argumente werden dann für die Geschwindigkeitsverhältnisse zweier Körper mit gleichem Volumen, aber ungleichem Gewicht angeführt, die dasselbe Medium sowohl aufwärts als auch abwärts bewegen.

Galilei beendet das Kapitel mit der Behauptung, dass sich leichtere Körper anfangs vor schwereren bewegen – eine Behauptung, die in Kapitel 22 erneut aufgegriffen wird.

Galilei untersucht die Kraft, die für die in Kapitel 8 erläuterten Bewegungen verantwortlich ist. Insbesondere untersucht er die Kraft, die nötig ist, um Holz unter Wasser zu halten. Er kommt zu dem Schluss, dass sich Holz mit einer Kraft nach oben bewegt, die dem Betrag entspricht, um den das Gewicht einer Wassermenge, die dem Holz entspricht, das Gewicht des Holzes übersteigt. Auf ähnliche Weise untersucht er die Kraft einer Bleikugel, die sich im Wasser nach unten bewegt, und kommt zu dem Schluss, dass sich die Kugel mit einer Kraft nach unten bewegt, die dem Betrag entspricht, um den sie das Gewicht einer gleich großen Wasserkugel übersteigt.

Dann greift er die Schlussfolgerung des vorhergehenden Kapitels auf: Bei Körpern aus unterschiedlichem Material aber identischer Größe ist das Verhältnis der Geschwindigkeiten ihrer natürlichen Abwärtsbewegungen dasselbe wie das Verhältnis ihrer Gewichte – und zwar nicht ihres Gewichtes als solchem, sondern des Gewichtes, das man durch Wiegen in dem Medium ermittelt, in dem die Bewegung stattfindet. Daraus erkennt Galilei, dass wir, wenn sich Objekte in einem Medium befinden und wir das Objekt auf einer Waage wiegen, nicht das Eigengewicht des Objekts haben, da der Auftrieb im Medium es immer verändern wird. Er schlägt vor, dass, wenn die Objekte in einem Vakuum gewogen werden könnten, hypothetisch das Eigengewicht ermittelt werden könnte.

Aristoteles führte mehrere Argumente an, um die Existenz eines Vakuums zu leugnen. So geht er beispielsweise davon aus, dass Bewegung nicht augenblicklich stattfinden kann, und versucht dann zu zeigen, dass Bewegung in einem Vakuum augenblicklich stattfinden würde, wenn es ein solches gäbe. Da dies unmöglich ist, schlussfolgert er, dass auch ein Vakuum unmöglich ist. Weiter folgert er, dass sich derselbe Körper, falls Bewegung in einem Vakuum zeitlich begrenzt sein kann, gleichzeitig in einem Medium und in einem Vakuum bewegen wird, was seiner Ansicht nach unmöglich ist. Galilei argumentiert, Aristoteles habe seine Annahmen nicht beweisen können, da sie falsch seien und zu falschen Schlussfolgerungen führten. Insbesondere behauptet Galilei, Aristoteles gehe davon aus, dass das Verhältnis der Geschwindigkeiten desselben Körpers in verschiedenen Medien gleich dem Verhältnis der Dichte der Medien sei, was Galilei in Kapitel 8 widerlegte.

Aristoteles’ Beweis besagte auch, dass es unmöglich ist, dass eine Zahl zu einer anderen Zahl dasselbe Verhältnis hat wie eine Zahl zu Null. Galilei argumentiert, dass dies für geometrische Verhältnisse (z. B. das Verhältnis von a/b) zutrifft, nicht jedoch für arithmetische Verhältnisse (z. B. a - b). Würde man das Geschwindigkeitsverhältnis zudem vom Verhältnis im arithmetischen Sinne (d. h. einem Verhältnis von Differenzen) abhängig machen, ergäbe sich keine absurde Schlussfolgerung, und der Körper könnte sich im Vakuum genauso bewegen wie in einem Medium.

In einem Medium hängt die Bewegungsgeschwindigkeit eines Körpers von der Differenz zwischen seinem Gewicht und dem Gewicht des Mediums ab, durch das er sich bewegt. Ebenso hängt in einem Vakuum die Geschwindigkeit seiner Bewegung von der Differenz zwischen seinem eigenen Gewicht und dem des Mediums ab, aber da die Dichte des Vakuums null ist, entspricht die Differenz dem gesamten und tatsächlichen Gewicht des Körpers.

Galileo lehnt dann Aristoteles’ Behauptung ab, dass Bewegung im Vakuum augenblicklich erfolgen würde, da das Vakuum unendlich leichter ist als jedes Medium und dass Bewegung darin unendlich schneller wäre als in jedem Medium. Galileo akzeptiert die Prämisse von Aristoteles’ Argument, lehnt jedoch die Schlussfolgerung der augenblicklichen Bewegung ab. Vielmehr argumentiert er, dass die Bewegung in weniger Zeit stattfindet als die Bewegungszeit in anderen Medien.

Aristoteles behauptete, dass mit Ausnahme von Feuer alles, sogar die Luft selbst, in seinem eigenen Bereich Gewicht hat. Eine luftgefüllte Blase wiegt mehr als eine entleerte.

Galileo widerspricht dem: Es ist bekannt, dass Wasser in der Luft Gewicht hat und sich aufgrund seines Gewichts nach unten bewegt, aber es ist absurd zu glauben, dass Wasser in Wasser sinkt, da eine erste Wassermenge eine zweite Wassermenge nach oben verdrängen müsste. Wenn ein Teil des Wassers schwer ist und sich im Wasser nach unten bewegen muss, würde dies außerdem bedeuten, dass dieser Teil schwerer ist als ein anderer Teil des Wassers mit gleichem Volumen – was absurd wäre, da Wasser dann schwerer als Wasser wäre.

Was die luftgefüllte Blase angeht, so behält diese ihr Gewicht bei, falls ein Loch in der luftgefüllten Blase geöffnet wird, aber die Luft ohne Krafteinwirkung (d. h. ohne Überdruck) im Ball verbleibt. Falls die Luft jedoch mit Kraft in die Blase gepresst wird, wird die Luft in der Blase schwerer als freie und entweichende Luft. Galileo argumentiert auch, dass die Elemente, wenn sie sich an ihrem richtigen Platz befinden, weder schwer noch leicht sind. Wir spüren das Gewicht des Wassers nicht, wenn wir schwimmen. Körper, die leichter als Wasser sind, steigen auf, Körper, die schwerer als Wasser sind, sinken und Körper, die das gleiche Gewicht wie Wasser haben, steigen weder auf noch sinken sie.

Aristoteles definierte, dass die „absolut schwersten“ Dinge diejenigen sind, die unter allem anderen liegen und sich immer zum Zentrum des Universums hin bewegen, und er bezeichnet die „absolut leichtesten“ Dinge als diejenigen, die sich über alles andere erheben und sich immer nach oben und niemals nach unten bewegen. Somit ist die Erde das Schwerste und das Feuer das Leichteste. Denn wenn Feuer schwer wäre, würde es unter etwas bleiben, was nicht beobachtet wird. Galileo widerlegt, dass Aristoteles’ Argument nicht schlüssig ist, weil es ausreicht, dass Feuer weniger schwer ist als alles andere und nicht unbedingt schwerelos sein muss.

Aristoteles argumentierte, dass, falls Feuer Gewicht hätte, eine große Menge Feuer schwerer wäre als eine kleine Menge, sodass die große Menge langsamer aufsteigen würde. Ähnlich würde eine große Menge Erde langsamer fallen als eine kleine Menge, wenn Erde Leichtigkeit hätte. Die Erfahrung zeige jedoch das Gegenteil. Galileo widerlegt dies als ungültiges Argument, da das Gewicht eines Körpers durch das Medium, in dem er sich befindet, verändert wird. Mit anderen Worten: Feuer hat in der Luft kein Gewicht. Zweitens steigt eine größere Menge Feuer schneller auf als eine kleine Menge – dies wurde in Kapitel 8 gezeigt. Galileo schlägt vor, dass die richtige Art, über Feuer zu argumentieren, darin besteht, dass eine große Menge Feuer schwerer ist als eine kleine Menge Luft, aber nicht im Medium Luft, wo Feuer kein Gewicht hat, sondern in einem anderen Medium, das leichter ist als Feuer, oder sogar im Vakuum.

Galileo hinterfragt dann die Behauptung, dass die Erde am schwersten ist, obwohl wir nicht unter die Erde sehen können. Außerdem ist bekannt, dass Quecksilber die Erde dazu bringt, darauf zu schwimmen, sodass es offensichtlich Dinge gibt, die schwerer sind als Erde.

Da in jedem Medium das Gewicht schwerer Körper durch das Gewicht eines Teils dieses Mediums, der in seiner Größe dem Festkörper entspricht, verringert wird, ist es klar, dass das gesamte und unverminderte Gewicht von Festkörpern in einem Medium mit dem Gewicht Null erreicht wird. Ein solches Medium kann nur das Vakuum sein.

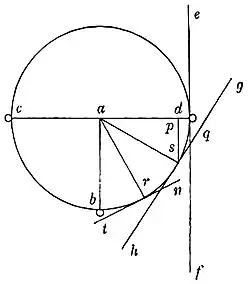
Galileo untersucht die Geschwindigkeiten von Körpern, die sich auf schiefer Ebenen bewegen; jedoch sind Teile seiner Argumentation unausgereift und enthalten Fehler. Galileo griff diese Diskussion später (mit Korrekturen) in seinen unveröffentlichten Vorlesungsnotizen Le Mecaniche wieder auf, in denen er sein neues abstraktes Konzept, das momento, verwendet, um sowohl das moderne Konzept des Moments als auch das des Drehimpulses grob zu beschreiben. Der Mathematiker Vincenzo Viviani fügte später eine Ergänzung zur zweiten Ausgabe von Discorsi e dimostrazioni matematiche hinzu, die sich auf Teile von Galileos verfeinerter Diskussion über schiefe Ebenen aus Le Mecaniche bezieht und diese einbezieht.

In der vorliegenden Diskussion erkennt Galileo in Kapitel 9, dass schwere Körper dazu neigen, sich mit derselben Kraft nach unten zu bewegen, die erforderlich ist, um sie anzuheben. Wenn wir also herausfinden können, wie viel Kraft erforderlich ist, um einen Körper auf einer schiefen Ebene nach oben zu ziehen, wissen wir auch, wie viel Kraft erforderlich ist, um den Körper auf der schiefen Ebene nach unten zu bewegen. Um diese Kraft zu messen, greift Galileo wieder auf den Hebel zurück, aber anstelle von parallel zueinander liegenden Hebelarmen ist ein Hebelarm in einem Winkel gebogen, sodass die auf den gebogenen Hebelarm ausgeübte Kraft abgeschwächt wird. Ein Gewicht, das am Ende des gebogenen Hebelarms positioniert ist, würde dann die gleiche Kraft erfahren, als befände sich das gleiche Gewicht auf einer schrägen Ebene, die tangential zur Drehung des gebogenen Hebelarms verläuft. Daraus lässt sich ein Verhältnis zwischen der Kraft an der schiefen Ebene und der vertikalen Kraft bilden, um das Verhältnis der Geschwindigkeiten zu ermitteln.

In seiner Argumentation verlangt Galileo, dass Objekte, die an einer Balkenwaage hängen, einen perfekten rechten Winkel zu vollkommen horizontalen Hebelarmen bilden, wodurch die Schnüre, an denen die Objekte hängen, parallel zueinander verlaufen. Galileo erkennt jedoch, dass diese Annahme fehlerhaft ist, da Körper zum Mittelpunkt der kugelförmigen Erde gezogen werden und die Schnüre daher tatsächlich Linien bilden würden, die sich im Mittelpunkt schneiden und nicht parallel verlaufen. Zur Verteidigung seiner Annahme erklärt Galileo: „Solchen Einwänden würde ich antworten, dass ich mich unter den schützenden Flügeln des übermenschlichen Archimedes verstecke, dessen Namen ich nie ohne Ehrfurcht erwähne. Denn er hat dieselbe Annahme in seiner Quadratur der Parabel getroffen ... doch wir dürfen in einem Moment des Zweifels nicht annehmen, dass seine Schlussfolgerung falsch ist, da er zuvor dieselbe Schlussfolgerung durch einen anderen geometrischen Beweis demonstriert hatte.“^[30]

Aristoteles behauptete, dass Kreisbewegungen in keinem Verhältnis zu geradlinigen Bewegungen stehen können, da eine gerade Linie in keinem Verhältnis zu einer Kurve steht und mit dieser nicht vergleichbar ist. Galileo lehnt dies ab und erklärt, dass dies so wäre, als würde man sagen, dass ein Dreieck und ein Quadrat nicht vergleichbar sind, weil das Dreieck nur drei Winkel hat, während das Quadrat vier hat. Selbst ein in ein Quadrat eingeschriebener Kreis hat ein gewisses Verhältnis, obwohl der Kreis gekrümmte Kanten hat, während das Quadrat gerade Kanten hat. Er argumentiert weiter, dass Aristoteles nicht erkannt habe, dass die Linien eine quantitative Beziehung zueinander haben, obwohl sie qualitativ unterschiedlich sind. Galileo behauptet außerdem, dass Aristoteles leichtfertig behauptet habe, es gäbe keine gerade Linie, die dem Umfang eines Kreises entspricht – Archimedes konnte in seinem Werk Über Spiralen beweisen, in dem er eine gerade Linie findet, die dem Umfang des Kreises um die Spirale der ersten Umdrehung entspricht.

Galileo stellt die Frage: Falls sich der Mittelpunkt einer rotierenden Murmelkugel (und ihr Schwerpunkt) im Zentrum des Universums befände, wäre ihre Rotationsbewegung dann erzwungen oder nicht? Galileo argumentiert, dass natürliche Bewegung auftritt, wenn Körper sich zu ihrem natürlichen Ort bewegen, und erzwungene Bewegung auftritt, wenn sie sich von ihrem natürlichen Ort entfernen. Daher ist klar, dass die Kugel, die sich um das Zentrum des Universums dreht, sich mit einer Bewegung bewegt, die weder natürlich noch erzwungen ist. Dies führt ihn zu der Argumentation, dass, falls ein einzelner Stern zum Himmel hinzugefügt würde, die Bewegung des Himmels nicht verlangsamt würde, da der Stern die Drehbewegung nur verlangsamen würde, wenn er von seinem natürlichen Ort entfernt würde, was jedoch bei Drehungen um den Mittelpunkt des Universums niemals geschieht, da es keine Aufwärts- oder Abwärtsbewegung gibt.

Galileo erkennt, dass diese Sichtweise eine weitere Frage aufwirft: Falls die rotierende Kugel, die im Zentrum des Universums platziert ist, weder eine natürliche Bewegung noch eine erzwungene Bewegung aufweist, würde die Kugel dann ewig weiterrotieren oder irgendwann zum Stillstand kommen? Falls ihre Bewegung natürlich wäre, würde sie sich scheinbar ewig bewegen; falls ihre Bewegung jedoch erzwungen ist, würde sie irgendwann zum Stillstand kommen. Galileo geht nie direkt auf diese Frage ein, sondern erklärt, dass sie besser in Kapitel 17 passt (wo sie ebenfalls unbeantwortet bleibt). Allerdings betrachtet Galileo den Fall einer homogenen, sich drehenden Kugel, die sich außerhalb des Zentrums des Universums befindet, und kommt zu dem Schluss, dass eine solche Bewegung erzwungen ist, da an der Achse, die die Kugel stützt, Widerstand vorhanden ist. Er argumentiert weiter, dass, falls die Achse unendlich klein wäre, kein Widerstand an der Achse entstehen würde und dass eine raue Oberfläche der Kugel dazu führen würde, dass Luft die Drehbewegung behindert. Bei einer heterogenen Kugel (d. h. bei der der Schwerpunkt vom geometrischen Zentrum abweicht) wechselt die Drehbewegung zwischen natürlicher und erzwungener Bewegung, da sich der Schwerpunkt um das geometrische Zentrum drehen würde.

Aristoteles argumentierte, dass Objekte sich aufgrund des Kontakts mit einem Beweger bewegen, aber da Geschosse ohne Kontakt mit einem Beweger fliegen, muss es so sein, dass die hinter dem Objekt strömende Luft seine Bewegung weiterleitet.

Galileo erhebt mehrere Einwände gegen diese Erklärung (von denen die meisten schon lange vor Galileo erkannt wurden): Die aufeinanderfolgenden Luftteile, die das Geschoss vorantreiben, würden immer beschleunigt werden, was den Annahmen von Aristoteles widerspricht. Die Erfahrung zeigt, dass Pfeile trotz starken Gegenwinds fliegen; ein Schiff, das mit Rudern gegen die Strömung angetrieben wird, bewegt sich noch lange weiter, nachdem die Ruder aus dem Wasser gezogen wurden; Eisenkugeln können über große Entfernungen geschleudert werden. Dennoch fallen Flachsfasern schneller zu Boden als die Eisenkugel. Schließlich kann sich eine Murmel lange Zeit drehen, ohne sich zu verschieben, sodass kein Raum für Luft bleibt, die gegen sie drücken könnte, und auch eine unter der Murmel platzierte Flamme wird nicht durch Luftströmungen gestört.

Stattdessen argumentiert Galileo, dass die Wurfbewegung zu einer erzwungenen Kraft führt, die dem Wurfkörper einen sich selbst erschöpfenden Impuls für seine Bewegung verleiht. Somit verändert diese erzwungene Kraft oder Impulskraft die Schwere eines Körpers, wenn er nach oben geworfen wird, und die Leichtigkeit des Körpers, wenn er nach unten geworfen wird.

Galileo vergleicht diese einwirkende Kraft mit der Temperatur eines Körpers: Falls ein Beweger auf den Körper einwirkt, ist dies in etwa so, als würde man Eisen ins Feuer legen. Sobald das Geschoss die Hand des Bewegers verlassen hat, nimmt die einwirkende Kraft ab, ähnlich wie Eisen seine Wärme verliert und zu seiner natürlichen Kälte zurückkehrt, wenn es aus dem Feuer genommen wird. Zur Frage, an welcher Stelle des Geschosses die ausgeübte Kraft wirkt, verlagert Galileo den Schwerpunkt der Frage, indem er erklärt, dass die ausgeübte Kraft dort wirkt, wo man glaubt, dass die Wärme im Geschoss gespeichert ist.

Anschließend vergleicht er die vom Beweger auf das bewegte Objekt übertragene Kraft mit der Kraft, die von einem Hammer auf eine Glocke übertragen wird: Beide sind zunächst still, doch der Hammer schlägt auf die Glocke und verleiht ihr einen Klang, der im Gegensatz zu ihrer natürlichen Stille steht, und mit der Zeit lässt der Klang allmählich nach, ähnlich wie eine auf ein Geschoss ausgeübte Kraft. Darüber hinaus argumentiert Galileo, dass es nicht die Luft ist, die weiterhin auf die Glocke schlägt, um den Klang zu erzeugen, sondern vielmehr die Glocke, die aufgrund der vom Hammer ausgeübten Kraft weiter schwingt.

Anschließend geht er näher auf die Veränderung des Gewichts aufgrund der ausgeübten Kraft ein: Obwohl der Körper durch die ausgeübte Kraft leichter wird, ist dieser Effekt nur vorübergehend, und während seiner gesamten Bewegung behält der Körper sein natürliches Gewicht bei, während die veränderte Schwere oder Leichtigkeit mit der Zeit nachlässt. Darüber hinaus behalten schwere Objekte ihren Impuls tendenziell länger bei als leichtere Objekte.

Galileo diskutiert, wie bestimmte Meinungen, so falsch sie auch sein mögen, dennoch Bestand haben, weil sie auf den ersten Blick den Anschein von Wahrheit erwecken, aber niemand sich die Mühe macht, ihre Glaubwürdigkeit zu prüfen. Er nennt als Beispiel eine weit verbreitete Fehlannahme, wonach Wasser selbst dafür verantwortlich sei, dass Objekte darin größer erscheinen. Er sagt, er habe mit diesem Phänomen experimentiert und festgestellt, dass eine tief im Wasser liegende Münze keineswegs größer, sondern vielleicht sogar kleiner erschien. Galileo kommt zu dem Schluss, dass das Missverständnis möglicherweise auf die Tradition zurückzuführen ist, im Sommer zur Dekoration Früchte in ein mit Wasser gefülltes Glasgefäß zu legen, und dass es die Krümmung des Gefäßes ist, die diesen Vergrößerungseffekt verursachte, und nicht direkt das Wasser.

Er schließt das Kapitel mit der Feststellung, dass es sicher ist, dass Geschosse in keiner Weise durch das Medium bewegt werden, sondern nur durch eine von einem Beweger ausgeübte Antriebskraft.

Galileo argumentiert, dass erzwungene Bewegung nicht endlos ist, dass die Kraft im Geschoss kontinuierlich abnimmt und dass eine Bewegung mit gleichbleibender Geschwindigkeit und konstanter Antriebskraft „sicherlich höchst absurd ist“.^[31] Galileo gab diese irrige Vorstellung später durch seine impliziten Ausführungen zur Trägheit in seinem Werk Discorsi e dimostrazioni matematiche auf.

Galileo gibt zu, dass er Schwierigkeiten hatte zu erklären, warum Objekte gegen Ende ihrer Bewegung beschleunigen. Obwohl er angibt, eine Lösung gefunden zu haben, ist die von ihm gelieferte Erklärung größtenteils falsch. Galileo lieferte später in seinem Werk Discorsi e dimostrazioni matematiche eine korrekte Beschreibung der natürlichen Beschleunigung: Der Gesprächspartner Salviati, der einen älteren Galileo repräsentiert, erklärt ausdrücklich, dass er keine Erklärung für die Ursache dieser Beschleunigung liefern würde, aber die hier gegebene Erklärung wird von dem Gesprächspartner Sagredo, der einen jüngeren Galileo repräsentiert, formuliert.

Aristoteles argumentierte gegen eine solche Beschleunigung und erklärte, dass natürliche Bewegung nicht durch „Ausstoß“ beschleunigt werde, da dies eine erzwungene Bewegung implizieren würde. Später argumentierten die Peripatetiker, dass es das Strömen der Luft hinter dem Geschoss sei, das die Beschleunigung verursache. Galileo entgegnet, dass dies nicht erkläre, warum ein rhombusförmiges Objekt beschleunigen würde, da die strömende Luft durch die Kanten der Form geteilt würde und daher nicht auf das Objekt treffen könne. Stattdessen argumentiert Galileo, dass ein schwerer fallender Körper sich zu Beginn langsamer bewegt, woraus folgt, dass der Körper zu Beginn seiner Bewegung weniger schwer ist als in der Mitte oder am Ende der Bewegung, und dass dies das Ergebnis einer Kraft ist. Die Frage lautet dann: Warum ist der Körper zu Beginn der Bewegung weniger schwer?

Er erklärt, dass, wenn ein schwerer Körper mit Kraft nach oben bewegt wird, eine Antriebskraft erforderlich ist, die größer ist als das Widerstandsgewicht, da sonst das Widerstandsgewicht nicht überwunden werden kann. Mit anderen Worten: Der Körper bewegt sich nach oben, vorausgesetzt, die ausgeübte Antriebskraft ist größer als das Widerstandsgewicht. Da diese Kraft jedoch mit der Zeit abnimmt, wird sie schließlich so schwach, dass sie das Gewicht des Körpers nicht mehr überwinden kann, und kehrt dann an ihrem Scheitelpunkt ihre Richtung um. Am Scheitelpunkt ist die ausgeübte Kraft jedoch nicht vollständig aufgebraucht, sondern übersteigt lediglich nicht mehr das Gewicht des Körpers und ist diesem gleich. In diesem Moment ist der Körper weder schwer noch leicht. Nach dem Scheitelpunkt nimmt die ausgeübte Kraft weiter ab, wobei das Gewicht des Körpers die Bewegung dominiert. Zu Beginn des Abstiegs vom Scheitelpunkt trägt die ausgeübte Kraft jedoch trotz ihrer geringeren Stärke im Vergleich zum Gewicht weiterhin zur Leichtigkeit des Körpers bei, weshalb die Bewegung des Abstiegs zu Beginn langsamer ist.

Galileo räumt dann ein, dass diese Erklärung für die Beschleunigung zuvor bereits vom Philosophen Hipparchos vorgebracht worden war, wie Ptolemäus in seinem Almagest zitiert, aber Galileo hielt Hipparchos’ Erklärung für unvollkommen. Sie wurde daher von späteren Philosophen abgelehnt.

Aristoteles und seine Anhänger glaubten, dass zwei entgegengesetzte Bewegungen nicht kontinuierlich miteinander verbunden sein können, und daher muss ein Stein, wenn er nach oben geworfen wird und wieder herunterfällt, zwangsläufig für einen bestimmten Zeitraum am Scheitelpunkt in Ruhe bleiben. Galileo widerlegt dies durch eine Reihe von Gegenargumenten, darunter einen Verweis auf das Werk De revolutionibus orbium coelestium von Nikolaus Kopernikus, in dem auf die aus zwei Kreisbahnen zusammengesetzte Bewegung eines Gestirn beschrieben wird. Galileo kommt zu dem Schluss, dass ein Zustand der Ruhe am höchsten Punkt nicht über einen bestimmten Zeitraum andauert, sondern in einem Augenblick durchlaufen wird. Diese Diskussion wird in Discorsi e dimostrazioni matematiche erneut aufgegriffen.

Aristoteles glaubte, dass, wenn die natürliche Bewegung unbegrenzt fortgesetzt würde, das Gewicht des Körpers und die Geschwindigkeit seiner Bewegung unbegrenzt zunehmen würden. Da jedoch unendliches Gewicht und unendliche Geschwindigkeit nicht existieren können, kommt er zu dem Schluss, dass eine solche Bewegung unmöglich wäre.

Galileo widerspricht und argumentiert stattdessen, dass die Geschwindigkeit nicht kontinuierlich zunimmt, und selbst wenn es möglich wäre, dass die Bewegung unbegrenzt fortgesetzt werden könnte, würde der Körper kein unendliches Gewicht und keine unendliche Geschwindigkeit erreichen. Wenn die auf einen Geschoss wirkende Kraft irgendwann aufgebraucht wäre, würde die Beschleunigung schließlich aufhören und das Objekt somit eine Endgeschwindigkeit erreichen. Diese Argumentation lässt darauf schließen, dass Galileo glaubte, dass die Endgeschwindigkeit sogar im luftleeren Raum erreicht wird. Galileo wird später in Discorsi e dimostrazioni matematiche erneut auf die Endgeschwindigkeit eingehen, jedoch mit der Erklärung, dass die Endgeschwindigkeit aufgrund des Luftwiderstands und nicht aufgrund einer Erschöpfung der auf das Geschoss wirkenden Kraft erreicht wird.

Beispielsweise lässt sich beobachten, dass eine Feder, die aus einer gewissen Höhe fällt, sich zu Beginn ihrer Bewegung langsam bewegt, später jedoch eine gleichmäßige Bewegung beibehält. Der Grund dafür liegt laut Galileo darin, dass weniger schwere Objekte nur eine Gegenkraft nach oben ausüben, die ihrem eigenen Gewicht entspricht, und da sie nicht sehr schwer sind, ist auch die ausgeübte Gegenkraft gering. Daher wird die ausgeübte Kraft schnell aufgebraucht, sodass das Objekt schnell eine gleichmäßige Fallbewegung erreicht. Er verweist auch auf die Analogie der Wärme: Ein glühendes Eisen kühlt schließlich ab, wenn ihm seine gesamte Wärme entzogen wird. Ebenso verändert sich ein Stein von leicht zu schwer, verliert seine gesamte erhaltene Leichtigkeit und erreicht schließlich eine gleichmäßige Geschwindigkeit. Darüber hinaus wäre die Annäherung an eine solche Endgeschwindigkeit asymptotisch, wie beispielsweise die Hyperbel, die in den Koniken des Apollonios von Perge behandelt wird, oder die erste Konchoidenkurve des Nikomedes im Kommentar des Eutocius von Askalon zu Archimedes’ Werk Über Kugel und Zylinder, Buch 2.

Averroes und seine Anhänger gingen davon aus, dass Elemente in ihrer eigenen Region schwer sind – eine These, die Galileo in Kapitel 11 ablehnte. Sie glaubten auch, dass eine Holzkugel mehr Luft enthält als eine Bleikugel, wodurch sich die Holzkugel schneller bewegt. Außerdem glaubten sie, dass Blei in der Luft schwerer ist als Eisen, weil Blei mehr Luft enthält als Eisen.

Galileo stellt fest, dass dieses Argument viele Unklarheiten enthält. Stattdessen schlägt er vor, dass Objekte, wenn sie ihre natürliche Bewegung aus der Ruhe heraus beginnen, mit einer Kraft beginnen, die ihrem Gewicht entspricht, aber entgegengesetzt ist (d. h. eine Hand oder ein Hilfsmittel, das das Objekt anfangs stützt, liefert diese Kraft). Infolgedessen beginnen schwerere Körper ihre Bewegung mit einer größeren Gegenkraft und fallen daher zu Beginn ihrer Bewegung langsamer als leichtere Körper, aber sobald die Gegenkraft erschöpft ist, fallen die schwereren Körper schneller als die leichteren, wie aus der Erfahrung hervorgeht.

Er räumt jedoch ein, dass seine vorgeschlagene Theorie noch einige Schwächen aufweist: Auch wenn schwerere Körper mit einer größeren einwirkenden Kraft beginnen, haben sie auch mehr Gewicht, das diese Kraft überwinden kann, was darauf hindeutet, dass schwere und leichte Körper mit gleicher Geschwindigkeit fallen sollten. Er antwortet jedoch, dass nicht das Gewicht die Gegenkraft erschöpft, sondern dass sich die Gegenkraft selbst erschöpft, ähnlich wie heißes Eisen abkühlt.

Er stellt dann fest, dass die aufgebrachte Kraft bei leichteren Objekten schneller nachlässt: Blei fliegt weiter und länger als Holz, wenn es aus einer Kanone abgeschossen wird; und wenn ein Pendel aus Holz und ein anderes aus Blei mit derselben Anfangsverschiebung gezogen werden und schwingen dürfen, schwingt das Bleipendel länger. Dies ist der früheste Hinweis auf Galileos Interesse am Pendel;^[4] er bezieht sich in seinen Discorsi e dimostrazioni matematiche erneut auf dieses Beispiel. Schließlich argumentiert er, dass die ausgeübte Kraft mit Wärme vergleichbar ist, sodass schwerere Körper sowohl ihre Wärme als auch ihren Schwung länger behalten als leichtere Körper. Aus diesen Beispielen schließt Galileo, dass leichtere Körper anfangs schneller fallen als schwerere Körper.

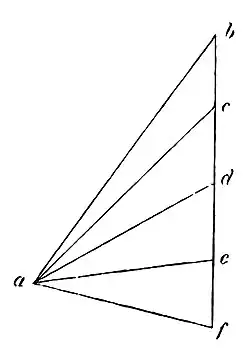
Galileo erinnert an die frühere Erklärung für die schiefe Ebene – dass schwere Objekte leicht zu schieben sind, wenn die Neigung gering ist, aber wenn sie in einem Winkel aus einer Kanone abgeschossen werden, scheint das Gegenteil der Fall zu sein. Er merkt jedoch an, dass der Unterschied hier darin besteht, dass das Objekt nicht mehr von einer Neigung gestützt wird, sondern von der einwirkenden Kraft getragen wird.

Um dieses Phänomen zu erklären, behauptet er, dass die ausgeübte Kraft stärker auf das wirkt, was sich ihrer Bewegung am meisten widersetzt. Wenn wir also Situationen finden, in denen der Widerstand eines Objekts größer ist, dann wird auch die ausgeübte Kraft stärker sein – das Drücken gegen die Bewegung eines Objekts bietet mehr Widerstand, als wenn das Objekt in Ruhe wäre oder sich in die gleiche Richtung bewegt. Mit anderen Worten: Der Widerstand des Objekts wird durch die Bewegung seines Gewichts erhöht. Wenn man beispielsweise Schlagball spielt, möchte der Schlagmann, dass der Ball in seine Richtung geworfen wird, damit er mehr Kraft auf ihn ausüben kann, da dessen Widerstand größer ist. Es ist schwieriger, eine Kraft auszuüben, wenn der Ball stillsteht, und noch schwieriger, wenn sich der Ball vom Schlagmann wegbewegt. Dasselbe gilt, wenn man einen Stein wirft, bei dem man zunächst die Hand zurückziehen muss, um zu werfen, und dasselbe gilt, wenn ein Stein mit einer Schleuder abgeschossen wird.

Unter diesen Beobachtungen argumentiert Galileo, dass beim Abfeuern einer Kanonenkugel die Eisenkugel mehr Widerstand in ihrer Bewegung leistet, wenn die Kanone eher vertikal als horizontal ausgerichtet ist, und somit gerader über eine längere Distanz und Zeit fliegt. Außerdem kann die Kugel bei einem vertikalen Kanonenschuss ihre Flugbahn nicht umkehren, bis die auf sie wirkende Kraft erschöpft ist (dies widerspricht den Aussagen in Kapitel 19, wo davon ausgegangen wird, dass die auf sie wirkende Kraft dem Gewicht am Scheitelpunkt entspricht), was bei einem horizontalen Schuss jedoch nicht der Fall ist.

• Galileo Galilei: De Motu. In: Antonio Favaro (Hrsg.): Le opere de Galileo Galilei. Band 1. Tip. di G. Barbèra, Florenz 1890, S. 243–419 (Latein, archive.org [PDF; 17,8 MB; abgerufen am 23. August 2025]). 
• Galileo Galilei: On Motion and On Mechanics. The University of Wisconsin Press, 1960 (englisch, Latein: De Motu. 1590. Übersetzt von Israel E. Drabkin). 

• Friedrich Klemm: Der junge Galilei und seine Schriften De motu und Le mecaniche. In: Ernst Brüche (Hrsg.): Sonne steh still: 400 Jahre Galileo Galilei. Sein heutiges Bild. Mosbach, Physik, 1964, S. 68–81. 
• Raymond Fredette: Galileo's De Motu Antiquiora. Notes for a Repraisal. Band 164. Max-Planck Institute for the History of Science, 2001, ISSN 0948-9444, S. 165–181 (englisch, fundacionorotava.org [PDF; 143 kB; abgerufen am 23. August 2025]). 
• Raymond Fredette: Les De motu antiquiora de Galileo Galilei : le lancement de la carrière du filosofo-geometra. In: Philosophia Scientiæ. Band 21, Nr. 1, 2017, S. 55–70, doi:10.4000/philosphiascientiae.1240 (französisch, openedition.org [abgerufen am 23. August 2025]). 

• Collection of Galileo Galilei's Manuscripts and Related Translations. In: Institute and Museum of the History of Science. Archiviert vom Original (nicht mehr online verfügbar); abgerufen am 16. Januar 2025 (englisch). 

• Gravitation

1. ↑ Enrico Giusti, "Galileo's De motu antiquiora," Nuncius 13, no. 2 (1998), 427–60 (englisch).
2. ↑ Stillman Drake, Essays on Galileo and the History and Philosophy of Science, Volume 1, University of Toronto Press, 1999, p. 216 (englisch).
3. ↑ ^{a b} Galileo Galilei, I.E. Drabkin, Stillman Drake: On Motion and On Mechanics. University of Wisconsin, Madison 1960, S. 3 (englisch). 
4. ↑ ^{a b} Galileo Galilei, I.E. Drabkin, Stillman Drake: On Motion and On Mechanics. University of Wisconsin, Madison 1960, S. 108 (englisch). 
5. ↑ Galileo Galilei, I.E. Drabkin, Stillman Drake: On Motion and On Mechanics. University of Wisconsin, Madison 1960, S. 9 (englisch). 
6. ↑ Galileo Galilei, I.E. Drabkin, Stillman Drake: On Motion and On Mechanics. University of Wisconsin, Madison 1960, S. 10 (englisch). 
7. ↑ Galileo Galilei, I.E. Drabkin, Stillman Drake: On Motion and On Mechanics. University of Wisconsin, Madison 1960, S. 4 (englisch). 
8. ↑ Galileo Galilei: Older Works on Motion. In: European Cultural Heritage Online. Abgerufen am 4. September 2025 (englisch, Übersetzung von Raymond Fredette). 
9. ↑ Pierre Duhem: Études sur Léonard de Vinci. III:Les Précurseurs Parisiens de Galilée. Paris 1913 (französisch). 
10. ↑ Alexandre Koyré: Études Galiléennes. Paris 1939 (französisch). 
11. ↑ Ernest A. Moody: Galileo and Avempace: The Dynamics of the Leaning Tower Experiment (I). In: Journal of the History of Ideas. 12. Jahrgang, Nr. 2, April 1951, S. 163–193 (englisch). 
12. ↑ ^{a b} Ernest A. Moody: Galileo and Avempace: The Dynamics of the Leaning Tower Experiment (II). In: Journal of the History of Ideas. 12. Jahrgang, Nr. 3, Juni 1951, S. 375–422 (englisch). 
13. ↑ Raymond Fredette: Galileo's De Motu Antiquiora. Notes for a Repraisal. 2001, S. 179–181 (englisch). 
14. ↑ Stillman Drake: Galilei. Herder, Freiburg 1999, ISBN 3-926642-38-6, S. 49–52. 
15. ↑ Edward Grant: Planets, Stars and Orbs: The Medieval Cosmos, 1200-1687. Cambridge University Press, Cambridge 1994, ISBN 978-0-521-09456-6, S. 525 (englisch). 
16. ↑ Raymond Fredette: Galileo's De Motu Antiquiora. Notes for a Repraisal. 2001, S. 171–173 (englisch). 
17. ↑ Favoro, Opere, S. 367–408
18. ↑ Galileo Galilei: Dialogue on Motion between Alessandro and Domenico. In: European Cultural Heritage Online. Abgerufen am 4. September 2025 (englisch, in der Übersetzung von Raymond Fredette). 
19. ↑ Fredette, Dialogue on Motion, S. 115
20. ↑ Fredette, Dialogue on Motion, S. 116–121
21. ↑ Fredette, Dialogue on Motion, S. 123
22. ↑ Fredette, Dialogue on Motion, S. 131
23. ↑ Fredette, Dialogue on Motion, S. 131–135
24. ↑ Fredette, Dialogue on Motion, S. 135–138
25. ↑ Fredette, Dialogue on Motion, S. 139–140
26. ↑ Fredette, Dialogue on Motion, S. 141–148
27. ↑ Fredette, Dialogue on Motion, S. 149–152
28. ↑ Fredette, Dialogue on Motion, S. 152–155
29. ↑ Galileo Galilei, I.E. Drabkin, Stillman Drake: On Motion and On Mechanics. University of Wisconsin, Madison 1960, S. 3–5 (englisch). 
30. ↑ Galileo Galilei, I.E. Drabkin, Stillman Drake: On Motion and On Mechanics. University of Wisconsin, Madison 1960, S. 67 (englisch). 
31. ↑ Galileo Galilei, I.E. Drabkin, Stillman Drake: On Motion and On Mechanics. University of Wisconsin, Madison 1960, S. 85 (englisch).