Charron-Ring

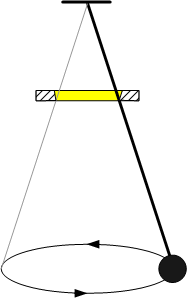
Der Ring wurde von dem französischen Physiker F. Charron im Jahre 1931 erfunden.^[1] Er dient zur Stabilisierung der Schwingungsebene des Pendels beim Foucaultschen Pendelversuch. Die ursprünglich ebene Schwingung eines Fadenpendels wird über kurz oder lang elliptisch. Ein elliptisch schwingendes Pendel ist aber für den Foucaultschen Pendelversuch unbrauchbar, weil sich seine Schwingungsform und Hauptschwingungsrichtung ständig ändern (siehe auch Sphärisches Pendel). Der Ring wird typischerweise im oberen Drittel des Pendels angebracht und so dimensioniert, dass das Seil den Ring kurz vor dem größten Ausschlag des Pendels berührt.^[2] In dieser Phase ist die Radialgeschwindigkeit nahe Null, während die Tangentialgeschwindigkeit den Maximalwert hat. Es gilt nun, diese Geschwindigkeit möglichst auf null zu bringen. Bei einem stark elliptisch schwingenden Pendel möchte das Seil am Ring entlangschlittern, wird aber durch die Reibungskraft festgehalten. Über den Ring wird nun ein Drehmoment auf das Pendel übertragen, wodurch dessen Drehimpuls verringert wird (ein eben schwingendes Pendel hat keinen Drehimpuls in der senkrechten Achse).

Der Ring ist sehr wirksam. Ein stark elliptisch schwingendes Pendel führt schon nach wenigen Pendelschlägen eine augenscheinlich ebene Bewegung aus. Es bleibt aber eine geringe Restelliptizität. Allerdings verbraucht der Charron-Ring die Energie des Pendels schneller. Um das Pendel in Bewegung zu halten, ist also eine zusätzliche Energiequelle erforderlich.^[2]

• Ekkehard W. Müller: Konzeption, Bau und Inbetriebnahme eines Foucaultschen Pendels am Kirchhoff-Institut für Physik. Staatsexamensarbeit, HD-KIP-03-03, 5. Mai 2003 (uni-heidelberg.de [PDF; 6,1 MB; abgerufen am 8. Juni 2025]). 

1. ↑ F. Charron: L’Expérience du Pendule de Foucault. In: NASA Astrophysics Data System. Abgerufen am 28. Juni 2024 (französisch). 
2. ↑ ^{a b} Gregory L. Baker and James A. Blackburn: The Pendulum - A Case Study in Physics. 1. Auflage. Oxford University Press, Oxford 2005, ISBN 978-0-19-856754-7, S. 87.