Boerdijk-Coxeter-Helix

Die Boerdijk-Coxeter-Helix^[1][2] (nach Arie Hendrick Boerdijk und Harold Scott MacDonald Coxeter), auch Tetrahelix^[3][4] oder Bernal-Spirale^[5][6] (nach John Desmond Bernal) genannt, ist eine Anordnung regulärer Tetraeder entlang einer Geraden im dreidimensionalen euklidischen Raum. Jedes Tetraeder teilt sich jeweils eine seiner Seitenflächen mit zwei benachbarten Tetraedern, ein Nachbar „links“ und einer „rechts“ (siehe die nebenstehende Abbildung).^[7][8] Aufgrund ihrer Geometrie ergibt sich hieraus eine schraubenförmige Anordnung der Tetraeder. Sie existiert in zwei chiralen Formen: einer rechtsgängigen und einer linksgängigen Helix. Die Definition der Boerdijk-Coxeter-Helix kann auf euklidische und sphärische Räume beliebiger Dimension erweitert werden.

Die Boerdijk-Coxeter-Helix kann durch explizite Berechnung ihrer Eckpunkte, Kanten und Seitenflächen konstruiert werden. Außerdem kann sie durch Schraubungen oder durch wiederholte Spiegelungen eines Ursprungstetraeders erzeugt werden. Diese Konstruktionen werden in den folgenden Abschnitten beschrieben.

Die Eckpunkte einer Boerdijk-Coxeter-Helix liegen auf der Oberfläche eines Zylinders. Sie sind gegeben durch:^{[8][1][6][9][10]}

${\displaystyle \mathbf {x} _{n}=\left({\begin{array}{ccc}\cos n\theta \\\sin n\theta \\n\xi \end{array}}\right).}$

Dabei sind ${\textstyle \theta =\pm \cos ^{-1}(-2/3)\approx \pm 131.810315^{\circ }}$, ${\textstyle \xi =1/{\sqrt {10}}}$ und ${\textstyle n}$ eine ganze Zahl (${\textstyle n\in \mathbb {Z} }$). Falls das Vorzeichen von ${\textstyle \theta }$ positiv gewählt wird, ergibt sich eine rechtsgängige Helix, ansonsten eine linksgängige.

Die Kanten der Boerdijk-Coxeter-Helix sind dadurch gegeben, dass die Ecken in Schritten von 1, 2 und 3 miteinander verbunden werden. Die Kanten sind also gegeben durch ${\textstyle (n,n+1)}$, ${\textstyle (n,n+2)}$ und ${\textstyle (n,n+3)}$, ${\textstyle n\in \mathbb {Z} }$.^[1] Die Seitenflächen ergeben sich unmittelbar aus den Kanten. Die Anzahl der Kanten der Schrittweite 1 pro Umdrehung ist gegeben durch ${\textstyle 2\pi /\theta \approx 2.731197}$.^[1] Da dies eine irrationale Zahl ist, besitzt keiner der Tetraeder dieselbe Orientierung.^[7]

Wenn die Punkte ${\textstyle (0,0,0)^{\top }}$, ${\textstyle (0,1,1)^{\top }}$, ${\textstyle (1,0,1)^{\top }}$ und ${\textstyle (1,1,0)^{\top }}$ als die Ecken des Ursprungstetraeders gewählt werden, ist die Schraubung, die die Ecken eines Tetraeders in die Ecken des nächsten Tetraeders transformiert, gegeben durch:^[11]

${\displaystyle \mathbf {S} ={\frac {1}{3}}\left({\begin{array}{cccc}2&2&1&0\\2&-1&-2&3\\-1&2&-2&3\\0&0&0&3\end{array}}\right).}$

Dabei ist die Matrix ${\textstyle \mathbf {S} }$ als erweiterte Abbildungsmatrix in homogenen Koordinaten zu interpretieren. Die Gleichung der Schraubungsachse ist ${\textstyle (-1/10,1/5,7/10)^{\top }+\lambda (2/{\sqrt {5}},1/{\sqrt {5}},0)^{\top }}$, der Schraubungswinkel ${\textstyle \theta =\cos ^{-1}(-2/3)}$ und der Schraubungsabstand ${\textstyle 1/{\sqrt {5}}}$. Letzterer ist größer als der Parameter ${\textstyle \xi }$ bei der Konstruktion über Eckpunkte, da das Ursprungstetraeder um den Faktor ${\textstyle {\sqrt {2}}}$ größer ist. Alle Tetraeder der Boerdijk-Coxeter-Helix lassen sich erzeugen, indem die Matrizen ${\textstyle \mathbf {S} ^{n},n\in \mathbb {Z} ,}$ auf das Ursprungstetraeder angewendet werden. Dadurch wird eine rechtsgängige Helix erzeugt. Um eine linksgängige Helix zu erzeugen, müssen die Ecken des Ursprungstetraeders in der folgenden Reihenfolge verwendet werden: ${\textstyle (0,0,0)^{\top }}$, ${\textstyle (1,1,0)^{\top }}$, ${\textstyle (1,0,1)^{\top }}$, ${\textstyle (0,1,1)^{\top }}$. Es ergibt sich folgende Matrix:

${\displaystyle \mathbf {S} ={\frac {1}{3}}\left({\begin{array}{cccc}-2&2&-1&3\\-2&-1&2&3\\1&2&2&0\\0&0&0&3\end{array}}\right).}$

Die Gleichung der Schraubungsachse ist ${\textstyle (7/10,1/5,-1/10)^{\top }+\lambda (0,1/{\sqrt {5}},2/{\sqrt {5}})^{\top }}$, der Schraubungswinkel ${\textstyle \theta =-\cos ^{-1}(-2/3)}$ und der Schraubungsabstand bleibt unverändert. Da das Ursprungstetraeder nur ganzzahlige Koordinaten enthält und die Matrizen ${\textstyle \mathbf {S} }$ nur rationale Einträge besitzen, zeigt dies, dass sich, trotz der oben beschriebenen Irrationalität des Rotationswinkels ${\textstyle \theta }$, alle Ecken der Boerdijk-Coxeter-Helix als rationale Zahlen darstellen lassen.

Es seien ${\textstyle \mathbf {a} _{0}=(0,0,0)}$, ${\textstyle \mathbf {b} _{0}=(0,1,1)}$, ${\textstyle \mathbf {c} _{0}=(1,0,1)}$ und ${\textstyle \mathbf {d} _{0}=(1,1,0)}$ die Ecken des Ursprungstetraeders, die, wie notiert, als Zeilenvektoren zu lesen sind. Wenn der Punkt ${\textstyle \mathbf {a} _{0}}$ durch die von ${\textstyle (\mathbf {b} _{0},\mathbf {c} _{0},\mathbf {d} _{0})}$ aufgespannte, ${\textstyle \mathbf {a} _{0}}$ gegenüberliegende Seitenfläche des Tetraeders gespiegelt wird, wird ein neuer Eckpunkt ${\textstyle \mathbf {a} _{1}=-\mathbf {a} _{0}+{\frac {2}{3}}(\mathbf {b} _{0}+\mathbf {c} _{0}+\mathbf {d} _{0})}$ erzeugt. Die Koordinaten des durch die Spiegelung erzeugten Tetraeders ${\textstyle \mathbf {a} _{1},\mathbf {b} _{0},\mathbf {c} _{0},\mathbf {d} _{0}}$ lassen sich durch die folgende Matrixtransformation beschreiben:^[12]

${\displaystyle \left({\begin{array}{c}\mathbf {a} _{1}\\\mathbf {b} _{0}\\\mathbf {c} _{0}\\\mathbf {d} _{0}\\\end{array}}\right)=\mathbf {M} _{\mathrm {a} }\left({\begin{array}{c}\mathbf {a} _{0}\\\mathbf {b} _{0}\\\mathbf {c} _{0}\\\mathbf {d} _{0}\\\end{array}}\right)=\left({\begin{array}{cccc}-1&{\frac {2}{3}}&{\frac {2}{3}}&{\frac {2}{3}}\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{array}}\right)\left({\begin{array}{c}\mathbf {a} _{0}\\\mathbf {b} _{0}\\\mathbf {c} _{0}\\\mathbf {d} _{0}\\\end{array}}\right).}$

Dabei ist das Element, das durch die 4×4-Matrix transformiert wird, eine 4×3-Matrix, in der die vier Punkte als Zeilenvektoren enthalten sind. Analoge Matrixtransformationen können für die Spiegelungen in den übrigen drei Seitenflächen des Tetraeders berechnet werden. Diese Matrizen seien mit ${\textstyle \mathbf {M} _{\mathrm {b} }}$, ${\textstyle \mathbf {M} _{\mathrm {c} }}$ und ${\textstyle \mathbf {M} _{\mathrm {d} }}$ bezeichnet. Damit lässt sich eine Matrix ${\textstyle \mathbf {M} =\mathbf {M} _{\mathrm {d} }\mathbf {M} _{\mathrm {c} }\mathbf {M} _{\mathrm {b} }\mathbf {M} _{\mathrm {a} }}$ berechnen, die aus vier Ecken eines Tetraeders vier neue berechnet:^[12]

${\displaystyle \left({\begin{array}{c}\mathbf {a} _{1}\\\mathbf {b} _{1}\\\mathbf {c} _{1}\\\mathbf {d} _{1}\\\end{array}}\right)=\mathbf {M} \left({\begin{array}{c}\mathbf {a} _{0}\\\mathbf {b} _{0}\\\mathbf {c} _{0}\\\mathbf {d} _{0}\\\end{array}}\right)={\frac {1}{81}}\left({\begin{array}{cccc}-81&54&54&54\\-54&-45&90&90\\-90&6&15&150\\-150&10&106&115\end{array}}\right)\left({\begin{array}{c}\mathbf {a} _{0}\\\mathbf {b} _{0}\\\mathbf {c} _{0}\\\mathbf {d} _{0}\\\end{array}}\right).}$

Alle Tetraeder der Boerdijk-Coxeter-Helix lassen sich erzeugen, indem die Matrizen ${\textstyle \mathbf {M} ^{n},n\in \mathbb {Z} ,}$ auf das Ursprungstetraeder angewendet werden. Dadurch wird eine rechtsgängige Helix erzeugt. Eine linksgängige Helix wird durch eine Permutation der generierenden Matrizen mit umgekehrten Vorzeichen erzeugt, beispielsweise ${\textstyle \mathbf {M} =\mathbf {M} _{\mathrm {a} }\mathbf {M} _{\mathrm {d} }\mathbf {M} _{\mathrm {c} }\mathbf {M} _{\mathrm {b} }}$.^[12] Auch bei dieser Konstruktion zeigt sich, dass sich alle Ecken der Boerdijk-Coxeter-Helix als rationale Zahlen darstellen lassen.

Im Video in diesem Abschnitt werden zwei Boerdijk-Coxeter-Helices, jeweils bestehend aus 30 Tetraedern, visualisiert. Die obere Helix ist rechtsgängig, die untere linksgängig. Beide Helices rotieren während des gesamten Videos, um ihre Geometrie besser zu veranschaulichen. Die obere Helix rotiert im Gegenuhrzeigersinn, die untere im Uhrzeigersinn (wenn die Helices von rechts aus entlang ihrer Achse betrachtet werden). Am Anfang des Videos werden die Tetraeder durch ihre Seitenflächen visualisiert. Während die Helices rotieren, kann beobachtet werden, dass ihre Ecken horizontal von links nach rechts entlang des oben beschriebenen Zylinders angeordnet sind.

Nach zwei Umdrehungen werden die Kanten der Tetraeder langsam eingeblendet. Die Kanten der Schrittweite 1 (siehe den Abschnitt Konstruktion über Eckpunkte) werden cyanfarben dargestellt. Sie haben dieselbe Windungsrichtung wie die zugehörige Tetraederhelix: die obere cyanfarbige Helix ist rechtsgängig, die untere linksgängig. Wie oben beschrieben ist der Winkel zwischen zwei aufeinanderfolgenden Ecken der Helix ${\textstyle \approx 131.810315^{\circ }}$. Daraus folgt, dass die Ecke ${\textstyle \mathbf {x} _{30}}$ mit der Ecke ${\textstyle \mathbf {x} _{0}}$ einen sehr kleinen Winkel von ${\textstyle \approx -5.690553^{\circ }}$ bezüglich der Zylinderachse einschließt.^[10] Die cyanfarbige Helix windet sich also in 30 Schritten etwas weniger als elfmal um die Zylinderachse. Beim Betrachten des Videos ist zu beachten, dass die cyanfarbige Helix 33 Ecken (32 Kanten) umfasst, da 30 Tetraeder dargestellt werden. Um die elf Windungen zu beobachten, muss also beispielsweise die erste Ecke mit der drittletzten verglichen werden.

Die zwei Sätze an Kanten der Schrittweite 2 (entsprechend ${\textstyle n}$ gerade oder ungerade) werden magentafarben dargestellt. Sie haben die entgegengesetzte Windungsrichtung wie die zugehörige Tetraederhelix: die oberen magentafarbenen Helices sind linksgängig, die unteren rechtsgängig. Der Winkel zwischen zwei aufeinanderfolgenden Ecken jeder der beiden Helices ist ${\textstyle \approx -96.379370^{\circ }}$.^[13] In 15 Schritten winden sich die beiden Helices jeweils etwas mehr als viermal um die Zylinderachse. Da im Video 30 Tetraeder dargestellt werden, hat eine Helix 17 Ecken (16 Kanten) und die andere 16 Ecken (15 Kanten). Je nachdem, welche der beiden Helices betrachtet wird, muss also die erste Ecke mit der vorletzten oder letzten verglichen werden, um die vier Windungen zu beobachten.

Die drei Sätze an Kanten der Schrittweite 3 (entsprechend ${\textstyle n=0,1,2\mod 3}$) werden orangefarben dargestellt. Sie haben dieselbe Windungsrichtung wie die zugehörige Tetraederhelix: die oberen orangefarbenen Helices sind rechtsgängig, die unteren linksgängig. Der Winkel zwischen zwei aufeinanderfolgenden Ecken jeder der drei Helices ist ${\textstyle \approx 35.430945^{\circ }}$. In zehn Schritten winden sich die drei Helices jeweils etwas weniger als einmal um die Zylinderachse. Im Video hat jede der drei Helices elf Ecken (zehn Kanten). Daher kann die eine Windung an jeder der drei Helices beobachtet werden.

Die drei Arten der Kanten der Schrittweiten 1, 2 und 3 bilden jeweils schraubenförmige räumliche Polygone. Nachdem sie eingeblendet wurden, werden die Tetraeder langsam ausgeblendet. In den letzten beiden Umdrehungen werden die Boerdijk-Coxeter-Helices nur noch durch die drei Arten von Polygonen visualisiert.

In der ersten Abbildung in diesem Abschnitt wird eine Orthogonalprojektion der Ecken und Kanten einer aus 31 Ecken bestehenden Boerdijk-Coxeter-Helix entlang ihrer Achse dargestellt. Die Farbkodierung der Kanten ist identisch mit der im Video. Es kann beobachtet werden, dass die Ecken der Helix unregelmäßig auf der Mantelfläche des Zylinders verteilt sind. Die Ecken ${\textstyle \mathbf {x} _{0}}$ und ${\textstyle \mathbf {x} _{30}}$ sind die beiden am weitesten rechts liegenden Ecken, von denen jeweils nur eine cyanfarbene Kante ausgeht. Der Winkel von ${\textstyle \approx -5.690553^{\circ }}$ zwischen diesen beiden Ecken ist erkennbar. Die Abbildung veranschaulicht außerdem, dass die cyanfarbenen Kanten einen Zylinder im Inneren der Helix einhüllen. Sein Radius beträgt ${\textstyle 1/{\sqrt {6}}}$. Die zweite Abbildung in diesem Abschnitt zeigt eine aus Magnetstäben und Metallkugeln konstruierte Helix zusammen mit dem eingehüllten Zylinder.

Die Konstruktion der Boerdijk-Coxeter-Helix kann auf euklidische Räume beliebiger Dimension ${\textstyle d\geq 1}$ erweitert werden.^[8][12] Am einfachsten ist dies aus der oben beschriebenen Konstruktion durch Spiegelungen ersichtlich. Die Konstruktion beginnt mit einem regulären d-Simplex, bestehend aus den Punkten ${\textstyle \mathbf {x} _{0},\mathbf {x} _{1},\ldots ,\mathbf {x} _{d}}$. Aus diesem kann durch Spiegelung des Punktes ${\textstyle \mathbf {x} _{0}}$ in der durch ${\textstyle \mathbf {x} _{1},\mathbf {x} _{2},\ldots ,\mathbf {x} _{d}}$ bestimmten, ${\textstyle \mathbf {x} _{0}}$ gegenüberliegenden Hyperebene der nächste Punkt der Helix berechnet werden. Dies kann durch folgende Matrixtransformation beschrieben werden:^[12]

${\displaystyle \left({\begin{array}{c}\mathbf {x} _{n}\\\mathbf {x} _{n+1}\\\vdots \\\mathbf {x} _{n+d}\\\end{array}}\right)=\mathbf {T} \left({\begin{array}{c}\mathbf {x} _{n-1}\\\mathbf {x} _{n}\\\vdots \\\mathbf {x} _{n+d-1}\\\end{array}}\right)=\mathbf {T} ^{n}\left({\begin{array}{c}\mathbf {x} _{0}\\\mathbf {x} _{1}\\\vdots \\\mathbf {x} _{d}\\\end{array}}\right).}$

Hierbei ist ${\textstyle n\in \mathbb {Z} }$ und

${\displaystyle \mathbf {T} =\left({\begin{array}{ccccc}0&1&0&\cdots &0\\0&0&1&\cdots &0\\\vdots &\vdots &\vdots &\ddots &\vdots \\0&0&0&\cdots &1\\-1&{\frac {2}{d}}&{\frac {2}{d}}&\cdots &{\frac {2}{d}}\end{array}}\right).}$

Wie beim dreidimensionalen Fall bilden jeweils ${\textstyle d+1}$ aufeinanderfolgende Punkte ein d-Simplex.^[8]

Für ${\textstyle d=1}$ liefert diese Konstruktion eine Aneinanderreihung gleich langer Strecken. Für ${\textstyle d=2}$ ergibt sich ein durch zwei parallele Geraden begrenzter Streifen aus gleichseitigen Dreiecken, bei dem die Dreiecke abwechselnd mit einer ihrer Spitzen zu einer der beiden Geraden orientiert sind. Die nebenstehende Abbildung zeigt einen aus sechs Dreiecken bestehenden Ausschnitt aus einer zweidimensionalen Boerdijk-Coxeter-Helix. Im Gegensatz zu den Dimensionen ${\textstyle d\geq 3}$ sind die ein- und zweidimensionalen Helices achiral.^[12] Für die Fälle ${\textstyle d\leq 4}$ lässt sich aus der Konstruktion über Spiegelungen auch jeweils eine Konstruktion über Eckpunkte herleiten, bei der die Punkte durch Auswertung expliziter Formeln berechnet werden können.^[12]

Das nebenstehende Video zeigt eine Orthogonalprojektion einer vierdimensionalen Boerdijk-Coxeter-Helix. ^{Anm. 1} Die Helix besteht aus zwölf regulären 5-Simplexen (5-Zellen). Zunächst werden nur ihre Kanten visualisiert. Sie sind gegeben durch die Kanten der Schrittweite 1 (1 × cyan), 2 (2 × magenta), 3 (3 × orange) und 4 (4 × blau). Die Helix dreht sich um ihre Achse, um ihre Struktur zu veranschaulichen. Da sich die 5-Zelle und ihre Flächen in der Projektion gegenseitig durchdringen, wäre eine gemeinsame Darstellung aller 5-Zelle nur schwer interpretierbar. Daher werden die 5-Zelle einzeln nacheinander angezeigt. Jedes 5-Zell wird in der Orthogonalprojektion auf ein Doppeltetraeder abgebildet. Es umfasst zwei der fünf Tetraeder des 5-Zells. Die restlichen drei Tetraeder sind um die magentafarbene Kante innerhalb des Doppeltetraeders angeordnet. Während die 5-Zelle nacheinander angezeigt werden, kann beobachtet werden, dass das rechte Tetraeder, das mit der magentafarbenen Kante durch das Doppeltetraeder verbunden ist, erhalten bleibt, wenn das nächste 5-Zell eingeblendet wird. Die rechte magentafarbene Kante des Tetraeders wird zur neuen Mittelkante des Doppeltetraeders. Das Tetraeder, das erhalten bleibt, ist das Tetraeder, über das die benachbarten 5-Zelle in der Helix miteinander verbunden sind. Jedes 5-Zell besteht aus vier cyanfarbenen, drei magentafarbenen, zwei orangefarbenen und einer blauen Kante. Die zehn Seitenflächen des 5-Zells verteilen sich auf die sechs Flächen des Doppeltetraeders, eine Fläche, an denen die beiden Tetraeder des Doppeltetraeders aneinander grenzen, und drei Flächen, die aus den beiden Spitzen des Doppeltetraeders und jeweils einer weiteren Ecke gebildet werden.

Die Konstruktion der Boerdijk-Coxeter-Helix kann auf sphärische Räume beliebiger Dimension ${\textstyle d\geq 1}$ erweitert werden.^[8]

Die Grundlage der Konstruktionen in euklidischen Räumen ist ein reguläres räumliches Polygon ${\textstyle \ldots \mathbf {x} _{0}\mathbf {x} _{1}\mathbf {x} _{2}\ldots ,}$ wobei regulär bedeutet, dass alle Kanten ${\textstyle \mathbf {x} _{\mu }\mathbf {x} _{\mu +1}}$ und alle Diagonalen ${\textstyle \mathbf {x} _{\mu }\mathbf {x} _{\mu +\nu },\nu =2,3,\ldots ,d,}$ des Polygons gleich lang sind. In der oben beschriebenen Konstruktion über Schraubungen bewegt die Schraubung das räumliche Polygon einen Schritt (eine Ecke) weiter entlang des Polygons ${\textstyle (\mathbf {x} _{0}\mathbf {x} _{1}\ldots \mathbf {x} _{d}\mapsto \mathbf {x} _{1}\mathbf {x} _{2}\ldots \mathbf {x} _{d+1})}$. Daher sind auch alle weiteren Diagonalen ${\textstyle \mathbf {x} _{\mu }\mathbf {x} _{\mu +\nu }}$ für ${\textstyle \nu \geq d+1}$ gleich lang.^[8]

In einem spärischen Raum bleibt das Grundprinzip, das räumliche Polygon durch eine Transformation einen Schritt entlang sich selbst weiterzubewegen, erhalten. Die Schraubung muss dabei durch eine Isometrie ${\textstyle \mathbf {S} }$ im sphärischen Raum ersetzt werden. Bei geeigneter Wahl von ${\textstyle \mathbf {S} }$ stimmt nach ${\textstyle h}$ Anwendungen von ${\textstyle \mathbf {S} }$ die Ecke ${\textstyle \mathbf {x} _{h}}$ mit der Ecke ${\textstyle \mathbf {x} _{0}}$ überein: es entsteht ein geschlossenes räumliches Polygon ${\textstyle \mathbf {x} _{0}\mathbf {x} _{1}\ldots \mathbf {x} _{h-1}}$, das eine Helix aus d-Simplizes definiert. Das räumliche Polygon ist das Petrie-Polygon eines regulären Polytops.^[8]

In der Sphäre ${\textstyle S^{2}}$ im ${\textstyle \mathbb {R} ^{3}}$ (${\textstyle d=2}$) bestehen die Boerdijk-Coxeter-Helices aus gleichseitigen Dreiecken in einem regulären Polyeder. Das Petrie-Polygon ist dadurch definiert, dass zwei aufeinanderfolgende seiner Kanten, aber keine drei, zu einer Seitenfläche des regulären Polyeders gehören.^[14] Die erste Abbildung in diesem Abschnitt zeigt ein Ikosaeder, dessen Petrie-Polygon cyanfarben dargestellt ist. Das Petrie-Polygon ist ein räumliches Zehneck. In der obigen Notation ist also ${\textstyle h=10}$. Die Boerdijk-Coxeter-Helix besteht aus den zehn an das Petrie-Polygon angrenzenden Dreiecken. Die übrigen zehn Dreiecke des Ikosaeders gehören nicht zur Helix. Eine zweidimensionale Boerdijk-Coxeter-Helix aus zehn Dreiecken kann im dreidimensionalen Raum zur Boerdijk-Coxeter-Helix des Ikosaeders zusammengefaltet werden.

Die Mittelpunkte der Kanten des Petrie-Polygons liegen alle in einer Ebene,^[14] die als Coxeter-Ebene bezeichnet wird. Eine Orthogonalprojektion eines Polyeders in die Coxeter-Ebene liefert eine besonders symmetrische Darstellung des Polyeders. Dies ist in der zweiten Abbildung in diesem Abschnitt zu erkennen. Das Petrie-Polygon erscheint in dieser Projektion als planares Zehneck. Alle weiteren Kanten und Ecken des Ikosaeders liegen innerhalb des Petrie-Polygons.

Die obige Konstruktion kann auch auf das Oktaeder und das Tetraeder angewendet werden. Beim Oktaeder entsteht dadurch eine aus sechs Dreiecken bestehende Boerdijk-Coxeter-Helix (${\textstyle h=6}$). Die übrigen zwei Dreiecke des Oktaeders gehören nicht zur Helix. Die oben abgebildete zweidimensionale Boerdijk-Coxeter-Helix aus sechs Dreiecken kann im dreidimensionalen Raum zur Boerdijk-Coxeter-Helix des Oktaeders zusammengefaltet werden.

Beim Tetraeder grenzt das Petrie-Polygon an jede Seitenfläche an. Die Boerdijk-Coxeter-Helix besteht in diesem Fall aus allen vier Dreiecken des Tetraeders (${\textstyle h=4}$). Eine aus vier Dreiecken bestehende zweidimensionale Boerdijk-Coxeter-Helix kann zu einem Tetraeder zusammengefaltet werden. Sie ist ein Netz des Tetraeders.

In der Sphäre ${\textstyle S^{3}}$ im ${\textstyle \mathbb {R} ^{4}}$ (${\textstyle d=3}$) bestehen die Boerdijk-Coxeter-Helices aus Tetraedern in einem regelmäßigen Polytop. Von den sechs regelmäßigen Polytopen bestehen drei aus Tetraedern: das 5-Zell (Schläfli-Symbol ${\textstyle \{3,3,3\}}$), das 16-Zell (Schläfli-Symbol ${\textstyle \{3,3,4\}}$) und das 600-Zell (Schläfli-Symbol ${\textstyle \{3,3,5\}}$). Für jedes dieser Polytope existiert eine zugehörige Boerdijk-Coxeter-Helix.

Die Isometrie ${\textstyle \mathbf {S} }$ ist in ${\textstyle S^{3}}$ eine Doppelrotation um die Winkel ${\textstyle \xi _{1}}$ und ${\textstyle \xi _{2}}$.^[8] Eine Doppelrotation um ${\textstyle \xi _{1}}$ in der ${\textstyle x_{1}x_{2}}$-Ebene und um ${\textstyle \xi _{2}}$ in der ${\textstyle x_{3}x_{4}}$-Ebene lässt sich durch folgende Matrix darstellen:

${\displaystyle \mathbf {S} =\left({\begin{array}{cccc}\cos \xi _{1}&-\sin \xi _{1}&0&0\\\sin \xi _{1}&\cos \xi _{1}&0&0\\0&0&\cos \xi _{2}&-\sin \xi _{2}\\0&0&\sin \xi _{2}&\cos \xi _{2}\\\end{array}}\right).}$

Die Rotationswinkel ${\textstyle \xi _{1}}$ und ${\textstyle \xi _{2}}$ sind die Lösungen der Gleichung

${\displaystyle x^{4}-(c_{p}+c_{q}+c_{r})x^{2}+c_{p}c_{r}=0,}$

wobei ${\textstyle c_{p}=\cos ^{2}\pi /p,c_{q}=\cos ^{2}\pi /q,c_{r}=\cos ^{2}\pi /r}$ und ${\textstyle \{p,q,r\}}$ das Schläfli-Symbol des jeweiligen Polytops sind. Da die Boerdijk-Coxeter-Helices aus Tetraedern bestehen, ist ${\textstyle p=q=3}$. Die zu lösende Gleichung vereinfacht sich dadurch zu:

${\textstyle x^{4}-({\frac {1}{2}}+c_{r})x^{2}+{\frac {1}{4}}c_{r}=0.}$

Die Lösungen dieser Gleichung sind die Werte ${\textstyle x=\cos \pm {\frac {1}{2}}\xi _{\nu },\nu =1,2}$.^[8] Die durch ${\textstyle \xi _{1}}$ und ${\textstyle \xi _{2}}$ bestimmte Isometrie ${\textstyle \mathbf {S} }$ erzeugt das Petrie-Polygon der Boerdijk-Coxeter-Helix. Ein Petrie-Polygon ist in der Sphäre ${\textstyle S^{3}}$ im ${\textstyle \mathbb {R} ^{4}}$ dadurch definiert, dass drei aufeinanderfolgende seiner Kanten, aber keine vier, zu einem Petrie-Polygon eines begrenzenden Polyeders des regulären Polytops gehören, also in diesem Fall zu einem Tetraeder.^[15][16] Bei der Boerdijk-Coxeter-Helix im dreidimensionalen euklidischen Raum ist das schraubenförmige Polygon der Schrittweite 1 das Analogon zum Petrie-Polygon (siehe die Abschnitte Konstruktion über Eckpunkte und Visualisierung der Boerdijk-Coxeter-Helix).

Für das 600-Zell ist ${\textstyle r=5}$. Damit ergeben sich als Rotationswinkel ${\textstyle \xi _{1}=\pi /15=12^{\circ }}$ und ${\textstyle \xi _{2}=11\pi /15=132^{\circ }}$.^[8] Die Punkte der Boerdijk-Coxeter-Helix lassen sich explizit berechnen durch:

${\displaystyle \mathbf {x} _{n}=\left({\begin{array}{ccc}a\cos n\xi _{1}\\a\sin n\xi _{1}\\d\cos n\xi _{2}\\d\sin n\xi _{2}\end{array}}\right),}$

wobei ${\textstyle n=0,1,\ldots 29}$, ${\textstyle a={\sqrt {(1+3^{-1/2}5^{-1/4}\tau ^{3/2})/2}}}$, ${\textstyle d={\sqrt {(1-3^{-1/2}5^{-1/4}\tau ^{3/2})/2}}}$ und ${\textstyle \tau =(1+{\sqrt {5}})/2}$ sind.^[17] Die Kanten der Boerdijk-Coxeter-Helix sind, analog zum euklidischen Raum, dadurch gegeben, dass die Ecken in Schritten von 1, 2 und 3 miteinander verbunden werden.^[1] Die Boerdijk-Coxeter-Helix im 600-Zell besteht aus 30 Tetraedern, die einen Ring bilden, dessen Ecken auf einem Torus liegen.^[1]

Im nebenstehenden Video wird eine Boerdijk-Coxeter-Helix im 600-Zell visualisiert. Die Helix wird dabei perspektivisch vom ${\textstyle \mathbb {R} ^{4}}$ in den ${\textstyle \mathbb {R} ^{3}}$ projiziert. Das Projektionszentrum liegt auf der positiven ${\textstyle x_{4}}$-Achse etwas oberhalb des Nordpols der Sphäre ${\textstyle S^{3}}$. Aufgrund der Projektion erscheinen die Tetraeder nicht mehr als regelmäßig, obwohl sie das im ${\textstyle \mathbb {R} ^{4}}$ sind. Die Helix rotiert während des gesamten Videos, um ihre Geometrie besser zu veranschaulichen. Am Anfang des Videos werden die Tetraeder der Helix durch ihre Seitenflächen visualisiert.

Nach einer Umdrehung werden die Kanten der Tetraeder langsam eingeblendet. Die Kanten der Schrittweite 1 (das Petrie-Polygon) werden cyanfarben dargestellt. Die Helix hat dieselbe Windungsrichtung wie die zugehörige Tetraederhelix. Wie oben beschrieben ist der Winkel zwischen zwei aufeinanderfolgenden Ecken der Helix ${\textstyle 132^{\circ }}$. Die cyanfarbige Helix windet sich also in 30 Schritten genau elfmal um die kreisförmige Achse. Sie wird deshalb auch als 30/11-Helix bezeichnet.^{[18][10][19][13]}

Die zwei Sätze an Kanten der Schrittweite 2 werden magentafarben dargestellt. Sie haben die entgegengesetzte Windungsrichtung wie die zugehörige Tetraederhelix. Der Winkel zwischen zwei aufeinanderfolgenden Ecken jeder der beiden Helices ist ${\textstyle -96^{\circ }}$.^[13] In 15 Schritten winden sich die beiden Helices jeweils genau viermal um die kreisförmige Achse. Sie werden deshalb auch als 15/4-Helix bezeichnet.^[19][13]

Die drei Sätze an Kanten der Schrittweite 3 werden orangefarben dargestellt. Sie haben dieselbe Windungsrichtung wie die zugehörige Tetraederhelix. Der Winkel zwischen zwei aufeinanderfolgenden Ecken jeder der drei Helices ist ${\textstyle 36^{\circ }}$. In zehn Schritten winden sich die drei Helices genau einmal um die kreisförmige Achse. Je zwei der orangefarbenen Helices bilden eine Hopf-Verschlingung.

Nachdem die schraubenförmigen Polygone eingeblendet wurden, werden die Tetraeder langsam ausgeblendet. In der letzten Umdrehung wird die Helix nur noch durch die drei Arten von Polygonen visualisiert.

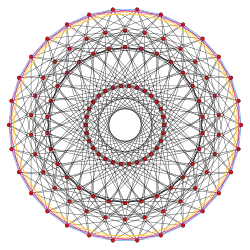
Die Abbildung in diesem Abschnitt zeigt die Lage einer Boerdijk-Coxeter-Helix in einer Orthogonalprojektion des 600-Zells in seine Coxeter-Ebene. Das 600-Zell wird durch seine Ecken und Kanten visualisiert. Die drei Arten von Kanten der Helix sind in denselben Farben wie im Video dargestellt. Das cyanfarbene Petrie-Polygon erscheint in dieser Projektion als regelmäßiges Dreißigeck, die magentafarbenen Helices als regelmäßige Fünfzehnecke und die orangefarbenen Helices als regelmäßige Zehnecke.

Die im Abschnitt Boerdijk-Coxeter-Helix im 600-Zell angegebenen Koordinaten stellen 30 der 120 Ecken des 600-Zells dar. Die übrigen 90 Ecken sind gegeben durch:

${\displaystyle \mathbf {x} _{n+30}=\left({\begin{array}{ccc}b\cos(n+{\frac {1}{2}})\xi _{1}\\b\sin(n+{\frac {1}{2}})\xi _{1}\\c\cos(n+{\frac {1}{2}})\xi _{2}\\c\sin(n+{\frac {1}{2}})\xi _{2}\end{array}}\right),\quad \mathbf {x} _{n+60}=\left({\begin{array}{ccc}c\cos(n+{\frac {1}{2}})\xi _{1}\\c\sin(n+{\frac {1}{2}})\xi _{1}\\-b\cos(n+{\frac {1}{2}})\xi _{2}\\-b\sin(n+{\frac {1}{2}})\xi _{2}\end{array}}\right),\quad \mathbf {x} _{n+90}=\left({\begin{array}{ccc}d\cos n\xi _{1}\\d\sin n\xi _{1}\\-a\cos n\xi _{2}\\-a\sin n\xi _{2}\end{array}}\right),}$

wobei ${\textstyle n=0,1,\ldots 29}$, ${\textstyle b={\sqrt {(1+3^{-1/2}5^{-1/4}\tau ^{-3/2})/2}}}$ und ${\textstyle c={\sqrt {(1-3^{-1/2}5^{-1/4}\tau ^{-3/2})/2}}}$ sind.^[17][20]

Wenn die Ecken ${\textstyle \mathbf {x} _{n}=(x_{1},x_{2},x_{3},x_{4})^{\top },n=0,1,\ldots ,119,}$ in die durch

${\displaystyle \left({\begin{array}{c}y_{1}\\y_{2}\\y_{3}\end{array}}\right)=\left({\begin{array}{c}2(x_{1}x_{3}+x_{2}x_{4})\\2(x_{2}x_{3}-x_{1}x_{4})\\x_{1}^{2}+x_{2}^{2}-x_{3}^{2}-x_{4}^{2}\end{array}}\right)}$

definierte Hopf-Abbildung eingesetzt werden, werden jeweils zehn Ecken des 600-Zells in der Spähre ${\textstyle S^{3}}$ auf einen Punkt der Sphäre ${\textstyle S^{2}}$ abgebildet. Die Ecken ${\textstyle \mathbf {x} _{n}}$, die auf denselben Punkt abgebildet werden, sind durch die Indizes ${\textstyle n=30i+j+3k}$, ${\textstyle i=0,\ldots ,3}$, ${\textstyle j=0,1,2}$ und ${\textstyle k=0,\ldots ,9}$ gegeben. Die Variablen ${\textstyle i}$ und ${\textstyle j}$ bestimmen dabei die Menge der Ecken, die auf denselben Punkt abgebildet werden, und die Variable ${\textstyle k}$ die Ecke innerhalb der jeweiligen Menge.

Die 120 Ecken des 600-Zells werden auf die zwölf Ecken eines Ikosaeders abgebildet.^[21][22] Umgekehrt können die Urbilder der 12 Ecken des Ikosaeders als diskrete Hopf-Fasern angesehen werden.^[11][22] Da die Hopf-Abbildung Großkreise in ${\textstyle S^{3}}$ auf Punke in ${\textstyle S^{2}}$ abbildet, bilden die Hopf-Fasern ein planares Zehneck, das ein Äquatorpolygon des 600-Zells darstellt. Jedes der zwölf Zehnecke bildet mit jedem anderen Zehneck eine Hopf-Verschlingung. Im Video im Abschnitt Visualisierung einer Boerdijk-Coxeter-Helix im 600-Zell sind drei der Zehnecke als orangefarbene Polygone dargestellt. Sie haben die Indizes ${\textstyle i=0}$ und ${\textstyle j=0,1,2}$ in der obigen Notation.

Aus den drei Hopf-Fasern der zu einem Dreieck des Ikosaeders gehörigen Ecken kann eine Boerdijk-Coxeter-Helix im 600-Zell konstruiert werden.^[21][11][22] Da die Zehnecke der drei Hopf-Fasern die schraubenförmigen Polygone der Schrittweite 3 festlegen, also insbesondere alle Ecken der Helix, müssen lediglich noch die beiden schraubenförmigen Polygone der Schrittweite 2 und das schraubenförmige Polygon der Schrittweite 1 bestimmt werden. Das 600-Zell kann daher aus 20 Boerdijk-Coxeter-Helices zusammengesetzt werden.^[11][22] Da die Zehnecke der Boerdijk-Coxeter-Helices polygonale Hopf-Verschlingungen bilden, sind alle Boerdijk-Coxeter-Helices gegenseitig miteinander verschlungen.

Die erste Abbildung in diesem Abschnitt zeigt zwei Boerdijk-Coxeter-Helices im 600-Zell. Die Helices werden dabei perspektivisch vom ${\textstyle \mathbb {R} ^{4}}$ in den ${\textstyle \mathbb {R} ^{3}}$ projiziert. Das Projektionszentrum liegt auf der positiven ${\textstyle x_{4}}$-Achse am Nordpol der Sphäre ${\textstyle S^{3}}$. Dies entspricht einer stereografischen Projektion der Ecken der Helices, wobei die projizierten Eckpunkte durch Geradenstücke verbunden werden. Im Folgenden wird diese Projektion vereinfachend stereografische Projektion genannt.

Die beiden Helices werden durch die Hopf-Fasern zweier Dreiecke des Ikosaeders erzeugt, die sich an ihren Kanten berühren. Dadurch wird bewirkt, dass sich die beiden Helices an den Seitenflächen berühren, die durch die beiden Hopf-Fasern erzeugt werden, die zu den gemeinsamen Ecken der zwei Dreiecke des Ikosaeders gehören.^[22] Die Abbildung zeigt außerdem, dass die beiden Boerdijk-Coxeter-Helices eine Hopf-Verschlingung bilden.

In der zweiten Abbildung in diesem Abschnitt werden drei Boerdijk-Coxeter-Helices gezeigt, deren zugehörige Dreiecke sich im Ikosaeder nicht berühren. Die Helices sind daher disjunkt. Auch hier kann beobachtet werden, dass jede der Helices mit den anderen Helices verschlungen ist.

Das Video in diesem Abschnitt zeigt, dass eine Hälfte des 600-Zells aus zehn Boerdijk-Coxeter-Helices aufgebaut ist. Zunächst wird eine Boerdijk-Coxeter-Helix, die einem Ursprungsdreieck auf dem Ikosaeder entspricht, angezeigt und gedreht, um ihre Geometrie zu veranschaulichen. In der zweiten Phase werden die drei Helices eingeblendet, die aus den am Ursprungsdreieck an ihren Kanten angrenzenden Dreiecken des Ikosaeders erzeugt werden. Sie grenzen an die ursprüngliche Helix an ihren Seitenflächen an. In der letzten Phase werden die sechs Helices eingeblendet, die aus den am Ursprungsdreieck an ihren Ecken angrenzenden Dreiecken des Ikosaeders erzeugt werden. Die sechs Helices berühren jeweils eine der drei Helices aus der zweiten Phase an ihren Seitenflächen. Am Ende des Videos sind zehn Helices, also 300 Tetraeder des 600-Zells, eingeblendet worden. Sie bilden eine Hälfte des 600-Zells und stellen topologisch einen Volltorus dar, dessen Oberfläche leicht nach innen und außen gefaltet ist. Die andere Hälfte des 600-Zells besteht aus den zehn zur anderen Hälfte des Ikosaeders gehörenden Boerdijk-Coxeter-Helices. Sie bilden im vierdimensionalen Raum einen zur visualisierten Hälfte des 600-Zells kongruenten Volltorus.^[21] Dies ist analog dazu, dass sich die 3-Sphäre aus zwei kongruenten Volltori zusammensetzen lässt.^[23][24][20] Da die übrigen zehn Helices durch die stereografische Projektion stark verzerrt dargestellt würden, werden sie im Video nicht visualisiert.

Ein Volltorus aus zehn Boerdijk-Coxeter-Helices im 600-Zell kann auch konstruiert werden, indem die zehn Dreiecke der Boerdijk-Coxeter-Helix des Ikoseders in der ersten Abbildung im Abschnitt Boerdijk-Coxeter-Helices in der zweidimensionalen Sphäre verwendet werden.^[22] Bei dieser Konstruktion wird allerdings der Rest des 600-Zells in zwei nicht zusammenhängende, aus jeweils fünf Boerdijk-Coxeter-Helices bestehende Volltori zerlegt.^[22]

Für das 16-Zell ist ${\textstyle r=4}$. Damit ergeben sich als Rotationswinkel ${\textstyle \xi _{1}=\pi /4=45^{\circ }}$ und ${\textstyle \xi _{2}=3\pi /4=135^{\circ }}$. Die Punkte der Boerdijk-Coxeter-Helix lassen sich explizit berechnen durch:

${\displaystyle \mathbf {x} _{n}=\left({\begin{array}{ccc}a\cos n\xi _{1}\\a\sin n\xi _{1}\\a\cos n\xi _{2}\\a\sin n\xi _{2}\end{array}}\right),}$

wobei ${\textstyle n=0,1,\ldots 7}$ und ${\textstyle a=1/{\sqrt {2}}}$ sind.^[25] Die Kanten der Boerdijk-Coxeter-Helix sind wiederum dadurch gegeben, dass die Ecken in Schritten von 1, 2 und 3 miteinander verbunden werden. Da ${\textstyle 9=1\mod 8}$ und ${\textstyle 10=2\mod 8}$ sind, bilden die Kanten der Schrittweite 3 ein geschlossenes Polygon, das, wie die Kanten der Schrittweite 1, ein Petrie-Polygon des 16-Zells ist. Die Boerdijk-Coxeter-Helix im 16-Zell besteht aus acht Tetraedern, die einen Ring bilden.

Im nebenstehenden Video wird eine Boerdijk-Coxeter-Helix im 16-Zell visualisiert. Die Helix wird dabei stereografisch projiziert. Diese Projektionsart wurde verwendet, um sicherzustellen, dass die Tetraeder, die sich im ${\textstyle \mathbb {R} ^{4}}$ nicht überlappen, sich nicht gegenseitig aufgrund der Projektion durchdringen. Aufgrund der Projektion erscheinen die Tetraeder stark verzerrt und nicht mehr als regelmäßig, obwohl sie das im ${\textstyle \mathbb {R} ^{4}}$ sind. Die Helix rotiert während des gesamten Videos, um ihre Geometrie besser zu veranschaulichen. Am Anfang des Videos werden die Tetraeder der Helix durch ihre Seitenflächen visualisiert.

Nach einer Umdrehung werden die Kanten der Tetraeder langsam eingeblendet. Die Kanten der Schrittweite 1 (das Petrie-Polygon) werden cyanfarben dargestellt. Wie oben beschrieben ist der Winkel zwischen zwei aufeinanderfolgenden Ecken der Helix ${\textstyle 135^{\circ }}$. Die cyanfarbige Helix windet sich also in acht Schritten genau dreimal um die kreisförmige Achse.

Die zwei Sätze an Kanten der Schrittweite 2 werden magentafarben dargestellt. Der Winkel zwischen zwei aufeinanderfolgenden Ecken jeder der beiden Helices ist ${\textstyle -90^{\circ }}$. In vier Schritten winden sich die beiden Helices jeweils genau einmal um die kreisförmige Achse. Sie stellen eine Hopf-Verschlingung dar.

Die Kanten der Schrittweite 3 werden orangefarben dargestellt. Der Winkel zwischen zwei aufeinanderfolgenden Ecken der Helix ist ${\textstyle 45^{\circ }}$. In acht Schritten windet sich die Helix genau einmal um die kreisförmige Achse.

Nachdem die schraubenförmigen Polygone eingeblendet wurden, werden die Tetraeder langsam ausgeblendet. Da es schwierig zu sehen ist, wie die Tetraeder, die die Boerdijk-Coxeter-Helix formen, miteinander verbunden sind, werden sie in den nächsten zwei Umdrehungen einzeln nacheinander in der Reihenfolge, in der sie in der Helix auftreten, angezeigt. In der letzten Umdrehung wird die Helix nur noch durch die drei Arten von Polygonen visualisiert.

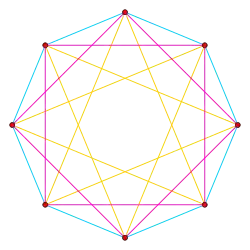
Die zweite Abbildung in diesem Abschnitt zeigt die Lage einer Boerdijk-Coxeter-Helix in einer Orthogonalprojektion des 16-Zells in seine Coxeter-Ebene. Das 16-Zell wird durch seine Ecken und Kanten visualisiert. Die drei Arten von Kanten der Helix sind in denselben Farben wie im Video dargestellt. Das cyanfarbene Petrie-Polygon erscheint in dieser Projektion als regelmäßiges Achteck, die magentafarbenen Helices als Quadrate und das orangefarbene Petrie-Polygon als überschlagenes Achteck.

Die acht Tetraeder der Boerdijk-Coxeter-Helix bilden topologisch einen Volltorus. Im 16-Zell existiert eine zweite Boerdijk-Coxeter-Helix. Wie oben beschrieben stellt das orangefarbene schraubenförmige Polygon der Schrittweite 3 ein zweites Petrie-Polygon des 16-Zells dar. Es kann zur Konstruktion der zweiten Helix verwendet werden. Wenn die dreifachen Winkelschrittweiten ${\textstyle 3\xi _{1}=3\pi /4=135^{\circ }}$ und ${\textstyle 3\xi _{2}=9\pi /4=\pi /4\mod 2\pi =45^{\circ }}$ in die im Abschnitt Boerdijk-Coxeter-Helix im 16-Zell angegebenen Formeln eingesetzt werden, ist ersichtlich, dass dies lediglich zur Vertauschung der Koordinaten ${\textstyle (x_{1},x_{2})}$ mit den Koordinaten ${\textstyle (x_{3},x_{4})}$ führt. Die zweite Boerdijk-Coxeter-Helix geht daher aus der ersten durch die durch folgende Matrix beschriebene Rotation hervor:

${\displaystyle \mathbf {R} =\left({\begin{array}{cccc}0&0&1&0\\0&0&0&1\\1&0&0&0\\0&1&0&0\end{array}}\right).}$

Dies zeigt, dass die beiden Boerdijk-Coxeter-Helices kongruent sind. Das 16-Zell kann aus ihnen zusammengesetzt werden.^[26] Wie beim 600-Zell ist dies analog dazu, dass sich die 3-Sphäre aus zwei kongruenten Volltori zusammensetzen lässt.

Für das 5-Zell ist ${\textstyle r=3}$. Damit ergeben sich als Rotationswinkel ${\textstyle \xi _{1}=2\pi /5=72^{\circ }}$ und ${\textstyle \xi _{2}=4\pi /5=144^{\circ }}$. Die Punkte der Boerdijk-Coxeter-Helix lassen sich explizit berechnen durch:

${\displaystyle \mathbf {x} _{n}=\left({\begin{array}{ccc}a\cos n\xi _{1}\\a\sin n\xi _{1}\\a\cos n\xi _{2}\\a\sin n\xi _{2}\end{array}}\right),}$

wobei ${\textstyle n=0,1,\ldots 4}$ und ${\textstyle a=1/{\sqrt {2}}}$ sind.^[25] Die Kanten der Boerdijk-Coxeter-Helix sind konzeptuell wiederum dadurch gegeben, dass die Ecken in Schritten von 1, 2 und 3 miteinander verbunden werden. Da ${\textstyle 3=-2\mod 5}$ ist, fallen aber die Kanten der Schrittweite 2 mit denen der Schrittweite 3 zusammen. Im 5-Zell besteht die Boerdijk-Coxeter-Helix aus fünf Tetraedern, die das 5-Zell komplett ausfüllen.

Eine Boerdijk-Coxeter-Helix aus fünf Tetraedern im euklidischen Raum ist ein Netz des 5-Zells. Sie lässt sich also im vierdimensionalen Raum zum 5-Zell zusammenfalten. Die Kanten der Schrittweiten 2 und 3, die in der Boerdijk-Coxeter-Helix im euklidischen Raum alle vorhanden sind, kommen durch das Zusammenfalten aufeinander zu liegen.

Im nebenstehenden Video wird die Boerdijk-Coxeter-Helix im 5-Zell visualisiert. Die Helix wird dabei stereografisch vom ${\textstyle \mathbb {R} ^{4}}$ in den ${\textstyle \mathbb {R} ^{3}}$ projiziert. Um eine einfacher zu verstehende Darstellung der Helix zu erreichen, werden die oben angegebenen Koordinaten so rotiert, dass eine Ecke am Südpol zu liegen kommt und die restlichen vier Ecken in einer Hyperebene auf der Nordhalbkugel der ${\textstyle S^{3}}$ liegen, die parallel zur Äquatorhyperebene liegt. Die Projektion entspricht daher dem üblichen Schlegeldiagramm des 5-Zells: in der Projektion liegen vier der Tetraeder innerhalb des fünften Tetraeders. Das äußere Tetraeder erscheint als reguläres Tetraeder. Die inneren Tetraeder verbinden jeweils eine Außenfläche mit der fünften Ecke, die in der Mitte der Projektion liegt. Diese Tetraeder erscheinen in der Projektion verzerrt. Im ${\textstyle \mathbb {R} ^{4}}$ sind alle fünf Tetraeder regulär.

Am Anfang des Videos werden die Tetraeder durch ihre halbtransparenten Flächen und die Kanten der Boerdijk-Coxeter-Helix visualisiert. Die Kanten der Schrittweite 1 (das Petrie-Polygon) werden cyanfarben dargestellt. Jedes Tetraeder enthält genau drei Kanten des Petrie-Polygons. Die Kanten der Schrittweite 2 werden magentafarben dargestellt. Die Helix dreht sich einmal, um ihre Geometrie zu veranschaulichen. Die Flächen werden während der Drehung langsam ausgeblendet. Danach stoppt die Rotation.

Da es schwierig zu sehen ist, wie die Tetraeder, die die Boerdijk-Coxeter-Helix formen, miteinander verbunden sind, werden im Anschluss die fünf Tetraeder einzeln nacheinander zusammen mit den Kanten der gesamten Helix angezeigt, zunächst die vier inneren und schließlich das äußere Tetraeder. Es kann beobachtet werden, dass jedes der Tetraeder mit genau einem vorausgegangenen und einem nachfolgenden Tetraeder über jeweils eine Fläche verbunden ist. Außerdem kann beobachtet werden, dass jedes neu eingeblendete Tetraeder eine Ecke auf dem cyanfarbenen Petrie-Polygon voranschreitet. Dies zeigt, dass die definierenden Eigenschaften der Boerdijk-Coxeter-Helix erfüllt sind. Die Helix rotiert zum Abschluss noch einmal. In dieser Umdrehung wird sie nur noch durch die zwei Arten von Kanten visualisiert.

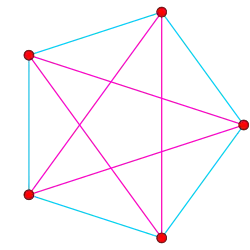
Die zweite Abbildung in diesem Abschnitt zeigt die Lage der Boerdijk-Coxeter-Helix in einer Orthogonalprojektion des 5-Zells in seine Coxeter-Ebene. Das 5-Zell wird durch seine Ecken und Kanten visualisiert. Die zwei Arten von Kanten der Boerdijk-Coxeter-Helix sind in denselben Farben wie im Video dargestellt. Das cyanfarbene Petrie-Polygon erscheint in dieser Projektion als regelmäßiges Fünfeck und das magentafarbene Polygon als Pentagramm.

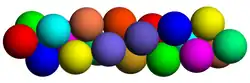
Arie Hendrick Boerdijk untersuchte Kugelpackungen, die lokal dichter sind als die dichteste Kugelpackung.^[7] Dabei beschrieb er mehrere Kugelpackungen mit unendlichem Volumen. Eine davon ist eine in einer Richtung unendlich ausgedehnte Anordnung von Kugeln, bei denen die Kugelmittelpunkte auf den Ecken der Boerdijk-Coxeter-Helix liegen. Jede Kugel berührt dadurch sechs Nachbarkugeln. Diese Kugelpackung weist eine etwas höhere lokale Dichte auf als die dichteste Kugelpackung. Sie kann aber nicht in alle Richtungen in derselben Dichte wie auf der Helix fortgesetzt werden.

John Desmond Bernal, dem die Arbeit von Boerdijk bekannt war,^[27] arbeitete an einer Theorie der Struktur der Flüssigkeiten.^[28] Um die Anordnung von Atomen in Flüssigkeiten zu untersuchen, führte er Experimente zu unregelmäßigen Kugelpackungen mit Metallkugeln durch. Dabei bestimmte er unter anderem die statistische Verteilung der Anzahl der Berührungen, die Kugeln in einer unregelmäßigen Kugelpackung mit anderen Kugeln haben. Im Rahmen dieser Experimente fand er Instanzen von Boerdijk-Coxeter-Helices in den unregelmäßigen Kugelpackungen.^[29]

Boerdijk-Coxeter-Helices im euklidischen Raum und im 600-Zell wurden in der Physik und Chemie verwendet, um Theorien für die Struktur von Stoffen zu entwickeln, beispielsweise für die Struktur der Kollagen-Tripelhelix;^[1][11][30] die Helix-Struktur von Polymeren, Biopolymeren und dicht gepackten Metallkristallen^[19] wie α- und β-Mangan;^[31][32] und die Selbstassemblierung von Nanopartikeln zu helikalen Strukturen.^[22] Außerdem wurden Nanodrähte aus Goldatomen in der Form einer Boerdijk-Coxeter-Helix hergestellt.^[33]

Die in Toronto aufgestellte Plastik Triad von Ted Bieler besteht aus drei Boerdijk-Coxeter-Helices.^[6]

Der vom japanischen Architekten Arata Isozaki entworfene Art Tower Mito ist eine etwa 100 m hohe Boerdijk-Coxeter-Helix, die aus 28 Tetraedern besteht.^[4]

Commons: Boerdijk-Coxeter-Helix – Sammlung von Bildern und Videos

1. ↑ ^{a b c d e f g} J. F. Sadoc, N. Rivier: Boerdijk–Coxeter helix and biological helices. In: European Physical Journal B. Band 12, Nr. 2, 1999, S. 309–318, doi:10.1007/s100510051009 (englisch). 
2. ↑ E. A. Lord, S. Ranganathan: The γ-brass structure and the Boerdijk–Coxeter helix. In: Journal of Non-Crystalline Solids. Band 334–335, 2004, S. 121–125, doi:10.1016/j.jnoncrysol.2003.11.069 (englisch). 
3. ↑ R. Buckminster Fuller: Synergetics: Explorations in the Geometry of Thinking. Macmillan Publishing Co., Inc., New York 1975, ISBN 0-02-065320-4, Abschnitt 930.00, S. 513–524 (englisch). 
4. ↑ ^{a b} Michael Elgersma, Stan Wagon: Closing a Platonic Gap. In: The Mathematical Intelligencer. Band 37, Nr. 1, 2015, S. 54–51, doi:10.1007/s00283-014-9456-2 (englisch). 
5. ↑ Paul J. Steinhardt, David R. Nelson, Marco Ronchetti: Bond-orientational order in liquids and glasses. In: Physical Review B. Band 28, Nr. 2, 1983, S. 784–805, doi:10.1103/PhysRevB.28.784 (englisch). 
6. ↑ ^{a b c} Chong Zheng, Roald Hoffmann, David R. Nelson: A Helical Face-Sharing Tetrahedron Chain with Irrational Twist, Stella Quadrangula, and Related Matters. In: Journal of the American Chemical Society. Band 112, Nr. 10, 1990, S. 3784–3791, doi:10.1021/ja00166a012 (englisch). 
7. ↑ ^{a b c} A. H. Boerdijk: Some Remarks Concerning Close-Packing of Equal Spheres. In: Philips Research Reoprts. Band 7, Nr. 4, 1952, S. 303–313 (englisch). 
8. ↑ ^{a b c d e f g h i j} H. S. M. Coxeter: The Simplicial Helix and the Equation ${\textstyle \tan n\theta =n\tan \theta }$. In: Canadian Mathematical Bulletin. Band 28, Nr. 4, 1985, S. 385–393, doi:10.4153/CMB-1985-045-5 (englisch). 
9. ↑ Michael Elgersma, Stan Wagon: An Asymptotically Closed Loop of Tetrahedra. In: The Mathematical Intelligencer. Band 39, Nr. 3, 2017, S. 40–45, doi:10.1007/s00283-016-9696-4 (englisch). 
10. ↑ ^{a b c} E. A. Zheligovskaya: Intersections of Boerdijk–Coxeter Helices in Three-Dimensional Euclidian Space. In: Crystallography Reports. Band 66, Nr. 3, 2021, S. 377–386, doi:10.1134/S1063774521030329 (englisch). 
11. ↑ ^{a b c d e} E. A. Lord, S. Ranganathan: Sphere packing, helices and the polytope {3,3,5}. In: European Physical Journal D. Band 15, Nr. 3, 2001, S. 335–343, doi:10.1007/s100530170149 (englisch). 
12. ↑ ^{a b c d e f g} A. C. Hurley: Some Helical Structures Generated by Reflexions. In: Australian Journal of Physics. Band 38, Nr. 3, 1985, S. 299–310, doi:10.1071/PH850299 (englisch). 
13. ↑ ^{a b c d} Alexander Talis: Helical substructures of 4D constructions that determine the structure of α-helices. In: Acta Crystallographica Section A: Foundations and Advances. Band 81, Nr. 3, 2025, S. 211–220, doi:10.1107/S2053273325001743 (englisch). 
14. ↑ ^{a b} H. S. M. Coxeter: Regular Polytopes. 3. Auflage. Dover Publications, New York 1973, ISBN 0-486-61480-8, S. 24–25 (englisch). 
15. ↑ H. S. M. Coxeter: Regular Polytopes. 3. Auflage. Dover Publications, New York 1973, ISBN 0-486-61480-8, S. 223–225 (englisch). 
16. ↑ H. S. M. Coxeter: Twisted honeycombs. American Mathematical Society, Providence, Rhode Island 1970, ISBN 0-8218-1653-5, S. 25 (englisch). 
17. ↑ ^{a b} H. S. M. Coxeter: Regular Polytopes. 3. Auflage. Dover Publications, New York 1973, ISBN 0-486-61480-8, S. 247–250 (englisch). 
18. ↑ E. A. Zheligovskaya, N. A. Bulienkov: Structures Consisting of Helices 30/11 and Their Possible Realization in Aqueous Systems. In: Physics of Wave Phenomena. Band 29, Nr. 2, 2021, S. 141–154, doi:10.3103/S1541308X21020163 (englisch). 
19. ↑ ^{a b c} Alexander Talis, Yaroslav Kucherinenko: Non-crystallographic helices in polymers and close-packed metallic crystals determined by the four-dimensional counterpart of the icosahedron. In: Acta Crystallographica Section B: Structural Science, Crystal Engineering and Materials. Band 79, Nr. 6, 2023, S. 537–546, doi:10.1107/S2052520623009393 (englisch). 
20. ↑ ^{a b} R. Mosseri, D. P. DiVincenzo, J. F. Sadoc, M. H. Brodsky: Polytope model and the electronic and structural properties of amorphous semiconductors. In: Physical Review B. Band 32, Nr. 6, 1985, S. 3974–4000, doi:10.1103/PhysRevB.32.3974 (englisch). 
21. ↑ ^{a b c} J. F. Sadoc: Helices and helix packings derived from the {3,3,5} polytope. In: European Physical Journal E. Band 5, Nr. 1 Supplement, 2001, S. 575–582, doi:10.1007/s101890170040 (englisch). 
22. ↑ ^{a b c d e f g h} Francesco Serafin, Jun Lu, Nicholas Kotov, Kai Sun, Xiaoming Mao: Frustrated self-assembly of non-Euclidean crystals of nanoparticles. In: Nature Communications. Band 12, 2021, 4925, doi:10.1038/s41467-021-25139-9 (englisch, inkl. Supplementary Information). 
23. ↑ Thomas F. Banchoff: Torus Decompostions of Regular Polytopes in 4-space. In: Marjorie Senechal (Hrsg.): Shaping Space – Exploring Polyhedra in Nature, Art, and the Geometrical Imagination. Springer-Verlag, New York 2013, ISBN 978-0-387-92713-8, S. 257–266, doi:10.1007/978-0-387-92714-5_20 (englisch). 
24. ↑ Gabor Toth: Glimpses of Algebra and Geometry. 2. Auflage. Springer-Verlag, New York 2002, ISBN 0-387-95345-0, S. 311–315, doi:10.1007/b98964 (englisch). 
25. ↑ ^{a b} H. S. M. Coxeter: Regular Polytopes. 3. Auflage. Dover Publications, New York 1973, ISBN 0-486-61480-8, S. 245 (englisch). 
26. ↑ Carlo H. Séquin: Symmetrical Hamiltonian Manifolds on Regular 3D and 4D Polytopes. In: Reza Sarhangi, Robert V. Moody (Hrsg.): Renaissance Banff: Mathematics, Music, Art, Culture. Bridges Conference, Southwestern College, Winfield, Kansas 2005, ISBN 0-9665201-6-5, S. 463–472 (englisch, Artikel auf bridgesmathart.org). 
27. ↑ J. D. Bernal: Geometry of the Structure of Monatomic Liquids. In: Nature. Band 185, Nr. 4706, 1960, S. 68–70, doi:10.1038/185068a0 (englisch). 
28. ↑ J. D. Bernal: The Bakerian Lecture, 1962. The Structure of Liquids. In: Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences. Band 280, Nr. 1382, 1964, S. 299–322, JSTOR:2415872 (englisch). 
29. ↑ J. D. Bernal: The Bakerian Lecture, 1962. The Structure of Liquids. In: Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences. Band 280, Nr. 1382, 1964, S. 307–308 und Abbildung 12, JSTOR:2415872 (englisch). 
30. ↑ Eric A. Lord: Helical Structures: The Geometry of Protein Helices and Nanotubes. In: Structural Chemistry. Band 13, Nr. 3/4, 2002, S. 305–314, doi:10.1023/A:1015863923728 (englisch). 
31. ↑ Alexander Talis, Ayal Everstov, Valentin Kraposhi: Crystal structures of alpha and beta modifications of Mn as packing of tetrahedral helices extracted from a four-dimensional {3,3,5} polytope. In: Acta Crystallographica Section B: Structural Science, Crystal Engineering and Materials. Band 76, Nr. 5, 2020, S. 948–954, doi:10.1107/S2052520620011154 (englisch). 
32. ↑ Alexander Talis, Ayal Everstov, Valentin Kraposhi: Spiral tetrahedral packing in the β-Mn crystal as symmetry realization of the 8D E₈ lattice. In: Acta Crystallographica Section A: Foundations and Advances. Band 77, Nr. 1, 2021, S. 7–18, doi:10.1107/S2053273320012978 (englisch). 
33. ↑ Yihan Zhu, Jiating He, Cheng Shang, Xiaohe Miao, Jianfeng Huang, Zhipan Liu, Hongyu Chen, Yu Han: Chiral Gold Nanowires with Boerdijk–Coxeter–Bernal Structure. In: Journal of the American Chemical Society. Band 136, Nr. 36, 2014, S. 12746–12752, doi:10.1021/ja506554j (englisch).