Black-Scholes-Modell

Das Black-Scholes-Modell (gesprochen ˌblæk ˈʃoʊlz)^[1] ist ein finanzmathematisches Modell zur Bewertung von Finanzoptionen. Es wurde von Fischer Black und Myron Samuel Scholes 1973 (nach zweimaliger Ablehnung durch renommierte Zeitschriften) veröffentlicht und gilt als ein Meilenstein der Finanzwirtschaft. Das Modell führte in der Finanzmathematik zu einem Paradigmenwechsel weg von Gleichgewichtsmodellen hin zu einer Theorie arbitragefreier Preise.^[2]

Robert C. Merton war ebenfalls essentiell an der Ausarbeitung beteiligt, veröffentlichte jedoch einen separaten Artikel. Gerechterweise müsste das Modell daher auch seinen Namen tragen, weshalb auch vom Black-Scholes-Merton-Modell gesprochen wird. Tatsächlich wurde Merton zusammen mit Scholes für die Entwicklung dieses Modells mit dem Preis der schwedischen Reichsbank für Wirtschaftswissenschaften 1997 geehrt; Fischer Black war bereits 1995 verstorben. Black setzte jedoch auch andere Bewertungsakzente als Scholes und Merton.^[3]

Die Ergebnisse von Black, Scholes und Merton wurden schon Anfang des 20. Jahrhunderts von Louis Bachelier (1900) für ein ähnliches Modell und von Vinzenz Bronzin (1908) einem anderen Ansatz folgend hergeleitet. Während die Arbeit des Ersteren durch Paul A. Samuelson im amerikanischen Raum seit den 1950er Jahren bekannt wurde, blieb das Werk des Letzteren lange in Vergessenheit. Bronzins Arbeit wurde erst um die Jahrtausendwende wieder berücksichtigt.^[4]

Das ursprüngliche Modell trifft einige idealisierende Annahmen:^[5]

1. Der Preis des Basiswertes, – also der Aktienpreis, folgt einer geometrischen brownschen Bewegung mit konstantem Drift und Volatilität.
2. Der Leerverkauf von Finanzinstrumenten ist uneingeschränkt möglich.
3. Es gibt keine Transaktionskosten oder Steuern. Alle Finanzinstrumente sind in beliebig kleinen Einheiten handelbar.
4. Von Abschluss bis Fälligkeit des Derivats gibt es keine Dividendenzahlung auf die zugrunde liegende Aktie.
5. Es gibt keine risikolose Möglichkeit zur Arbitrage (Arbitragefreiheit).
6. Finanzinstrumente werden kontinuierlich gehandelt.
7. Es existiert ein risikofreier Zinssatz ${\displaystyle r}$, der zeitlich konstant und für alle Laufzeiten gleich ist.

In Modellerweiterungen werden auch Dividendenzahlungen, stochastische Zinssätze oder stochastische Volatilitäten betrachtet.

Wir betrachten einen Zeitraum ${\displaystyle [0,T]}$ mit ${\displaystyle T\in (0,\infty )}$ und einen filtrierten Wahrscheinlichkeitsraum ${\displaystyle (\Omega ,{\mathcal {F}},\mathbb {F} ,\mathbb {P} )}$, wobei die Filtration ${\displaystyle \mathbb {F} }$ durch einen Standard-Wiener-Prozess ${\displaystyle W}$ erzeugt wird und die üblichen Bedingungen erfüllt. Nach den Annahmen bewegt sich der undiskontierte Aktienkurs ${\displaystyle S}$ gemäß einer geometrischen Brownschen Bewegung mit inkrementellen und dekrementellen Kursänderungen, d. h. $${\displaystyle \mathrm {d} S=\mu \,S\,\mathrm {d} t+\sigma \,S\,\mathrm {d} W}$$Dabei ist ${\displaystyle \mu }$ die erwartete Rendite des Aktienkurses, ${\displaystyle \sigma >0}$ die Volatilität und ${\displaystyle t\geq 0}$ die Zeit. ${\displaystyle \mathrm {d} W}$ kann als ein infinitesimaler Zuwachs von ${\displaystyle W_{t}}$ auf einem Zeitintervall der Länge ${\displaystyle \mathrm {d} t}$ angesehen werden, d. h. als eine normalverteilte Zufallsvariable mit Erwartungswert ${\displaystyle 0}$ und Varianz ${\displaystyle \mathrm {d} t}$. Der abgezinste Preisprozess ${\displaystyle X}$ von ${\displaystyle S}$ ist unter der Arbitragefreiheitsannahme ein Martingal bezüglich dem äquivalenten Martingalmaß ${\displaystyle \mathbb {P} ^{\ast }\sim \mathbb {P} }$, wobei die Dichte durch $${\displaystyle \left.{\frac {\operatorname {d} \!\mathbb {P} ^{\ast }}{\operatorname {d} \!\mathbb {P} }}\right\vert _{{\mathcal {F}}_{t}}=\exp \left(-\theta W_{t}-{\frac {1}{2}}\sigma ^{2}t\right)}$$ mit ${\displaystyle \theta ={\frac {\mu -r}{\sigma }}}$ dem Risikomarktpreis (englisch market price of risk) gegeben ist.^{[Anm. 1]} Mit dem Satz von Girsanow folgt, dass der Prozess ${\displaystyle W^{\ast }}$ definiert durch ${\displaystyle W_{t}^{\ast }=W_{t}+\theta t}$ für alle ${\displaystyle t\in [0,T]}$ ein Wiener-Prozess unter dem äquivalenten Martingalmaß ${\displaystyle \mathbb {P} ^{\ast }}$ ist.^{[Anm. 2]}

Analog lässt sich für ${\displaystyle n}$ Aktien ${\displaystyle S^{1},\dots ,S^{n}}$ und ${\displaystyle n}$ Standard-Wiener-Prozessen ${\displaystyle W^{1},\dots ,W^{n}}$, das mehrdimensionale Black-Scholes-Modell bilden:^[6]

${\displaystyle \mathrm {d} S^{i}=\mu _{i}\,S^{i}\,\mathrm {d} t+S^{i}\sum \limits _{j=1}^{n}\sigma _{ij}\,\mathrm {d} W^{j},\quad i=1,\dots ,n}$.

Das Black-Scholes-Modell kann als Grenzfall des zeit- und wertediskreten Binomialmodells nach Cox, Ross und Rubinstein interpretiert werden. Indem die Handelsintervalle immer kürzer gesetzt werden, ${\displaystyle \Delta t\to 0}$ nehmen die Sprünge ${\displaystyle u(\Delta t)}$ und ${\displaystyle d(\Delta t)}$ kontrolliert ab. Dadurch wird aus der konstanten risikofreien Zinsrate ein konstanter Momentanzins. Mit Hilfe des Satzes von Donsker und dem Skorochodschen Einbettungssatzes lässt sich die Konvergenz zur geometrischen brownschen Bewegung zeigen.

Die Aktienkursrenditen im diskreten Modell seien binomialverteilt. Sie konvergieren gegen eine Normalverteilung. Die Aktienkurse sind dann in jedem Zeitpunkt logarithmisch normalverteilt. In der Regel ist eine Schrittzahl von 100 ausreichend mit der Einschränkung exotischer Optionen oder Optionssensitivitäten.

Zur Herleitung der Black-Scholes-Differentialgleichung sind zwei gängige Ansätze üblich, nämlich entweder mittels Replizierung des Derivats oder mittels einer Wertsicherungsstrategie.^[7] Die Herleitung hiernach wird durch Letzteres motiviert. Zur Vereinfachung der Herleitung werden von Beginn an die eigentlich ex post ermittelten Stückanzahlen genutzt. Das risikolose Portfolio besteht aus einer Shortposition im Derivat und ${\displaystyle {\frac {\partial V}{\partial S}}}$ Stücke der Aktien.^{[Anm. 3]} Sei ${\displaystyle V=V(t,S)}$ in ${\displaystyle C^{2}((0,\infty )\times (0,\infty ))}$ der Wertprozess des Derivats. Mittels der Itō-Formel erhält man für die Änderungen des Wertes ${\displaystyle V}$ des Derivats die Formel^{[Anm. 4]}

$${\displaystyle \mathrm {d} V=\left({\frac {\partial V}{\partial t}}+\mu \,S{\frac {\partial V}{\partial S}}+{\frac {1}{2}}\,\sigma ^{2}\,S^{2}\,{\frac {\partial ^{2}V}{\partial S^{2}}}\right)\mathrm {d} t+\sigma \,S\,{\frac {\partial V}{\partial S}}\,\mathrm {d} W}$$

Mit den gegebenen Portfoliogewichten und den Preisprozessen für Aktie und Derivate lassen sich der Portfoliowert und die Wertänderungen des Portfolios über kurze Zeiträume formulieren. Der Portfoliowert ${\displaystyle P}$ ist ${\displaystyle P=-V+S\,{\frac {\partial V}{\partial S}}}$, also die Summe des negativen Wertes des Derivats plus des Wertes von ${\displaystyle {\frac {\partial V}{\partial S}}}$ Stück Aktien. Die Wertänderung ${\displaystyle \mathrm {d} P}$ des Portfolios über kurze Zeiträume lässt sich schreiben als$${\displaystyle \mathrm {d} P=-\mathrm {d} V+\mathrm {d} S\,{\frac {\partial V}{\partial S}}=\left(-{\frac {\partial V}{\partial t}}-{\frac {1}{2}}\,\sigma ^{2}\,S^{2}\,{\frac {\partial ^{2}V}{\partial S^{2}}}\right)\mathrm {d} t}$$Die Preisentwicklung des Portfolios hängt also weder von den zufälligen Preisänderungen des Aktienkurses aus dem Wienerprozess ${\displaystyle W}$ noch von der erwartete Aktienrendite ${\displaystyle \mu }$ ab. Der zweite Punkt ist eine wichtige Erkenntnis aus dem Black-Scholes-Modell. Da das Portfolio risikolos ist und laut Annahmen keine Arbitragemöglichkeiten bestehen, muss das Portfolio über kurze Zeiträume genau die risikolose Rendite ${\displaystyle r}$ erwirtschaften, also ${\displaystyle \mathrm {d} P=r\,P\,\mathrm {d} t}$. Durch Einsetzen in die letzte Gleichung erhält man die Black-Scholes-Differentialgleichung

$${\displaystyle {\frac {\partial V}{\partial t}}+r\,S{\frac {\partial V}{\partial S}}+{\frac {1}{2}}\,\sigma ^{2}\,S^{2}\,{\frac {\partial ^{2}V}{\partial S^{2}}}=r\,V}$$

Diese Gleichung ist unter den gegebenen Annahmen für alle Derivate gültig, die sich auf Grundlage des Preisprozesses für ${\displaystyle S}$ definieren lassen. Die Art des Derivats, für das die Gleichung gelöst werden soll, bestimmt die Randbedingungen für die Differentialgleichung.

Marek Musiela und Marek Rutkowski haben darauf hingewiesen, dass das in der Herleitung der Black-Scholes-Differentialgleichung verwendete Portfolio nicht selbst-finanzierend ist.^[8] Die Argumentation ist zwar intuitiv und liefert die Black-Scholes-Differentialgleichung. Finanzmathematisch ist die Herleitung jedoch problematisch. Musiela und Rutkowski geben auch eine finanzmathematisch überzeugende Herleitung an.^[9]

Die zur Black-Scholes-Formel führende Analyse betrachtet ein beliebiges Derivat, dessen Basiswert eine Aktie ohne Dividendenausschüttung ist. Der Grundgedanke ist, aus dem Derivat und der Aktie ein risikoloses Portfolio zu konstruieren.^[10] „Risikolos“ meint in diesem Zusammenhang, dass der Wert des Portfolios für kurze Zeiträume – gleichbedeutend mit kleinen Änderungen des Aktienkurses – nicht vom Kurs der Aktie abhängt. Europäische Optionen erbringen am Ende der Laufzeit (bei ${\displaystyle t=T}$) die Kapitalflüsse ${\displaystyle {\mathit {CF_{\text{call}}}}(T)=\max\{S-K;0\}}$ für eine Kaufoption (englisch Call) beziehungsweise ${\displaystyle {\mathit {CF_{\text{put}}}}(T)=\max\{K-S;0\}}$ für eine Verkaufsoption (englisch Put).

Der faire Preis der Option kann über verschiedene Argumentationen hergeleitet werden. Er kann als diskontierter Erwartungswert der genannten Auszahlungen in ${\displaystyle T}$ dargestellt werden, wobei der Erwartungswert bezüglich des risikoneutralen Maßes zu bilden ist. Ein anderer Weg zur Herleitung einer expliziten Formel für die Optionspreise besteht in der Lösung der Black-Scholes-Differentialgleichung, wobei die Auszahlungen bei Fälligkeiten als Randbedingungen berücksichtigt werden.^[11]

Auf beiden Wegen erhält man die Preisformel nach Black-Scholes für eine europäische Kaufoption$${\displaystyle C(S,t)=S\Phi (d_{1})-Ke^{-r(T-t)}\Phi (d_{2})}$$

beziehungsweise für eine europäische Verkaufsoption$${\displaystyle P(S,t)=-S\Phi (-d_{1})+Ke^{-r(T-t)}\Phi (-d_{2})}$$

wobei ${\displaystyle d_{1}={\frac {\ln({\frac {S}{K}})+(r+{\frac {\sigma ^{2}}{2}})(T-t)}{\sigma {\sqrt {T-t}}}}}$ und ${\displaystyle d_{2}={\frac {\ln({\frac {S}{K}})+(r-{\frac {\sigma ^{2}}{2}})(T-t)}{\sigma {\sqrt {T-t}}}}=d_{1}-\sigma {\sqrt {T-t}}}$ mit ${\displaystyle \Phi (x)=\int _{-\infty }^{x}{\frac {1}{\sqrt {2\pi }}}\exp {\Bigl (}-{\frac {z^{2}}{2}}{\Bigr )}\,\mathrm {d} z}$ die Verteilungsfunktion der Standardnormalverteilung.

Der Wert einer Option ist also durch fünf Parameter bestimmt:

${\displaystyle S}$: aktueller Aktienkurs

${\displaystyle r}$: mit der Restlaufzeit der Option kongruenter Zinssatz

${\displaystyle \sigma }$: Die zukünftige Volatilität des Basiswertes. Diese ist bei Vertragsabschluss die einzige unbekannte Größe und damit letztlich Gegenstand der Preisfindung zwischen den Vertragsparteien.

${\displaystyle T-t}$: Restlaufzeit der Option mit Gesamtlaufzeit ${\displaystyle T}$ zum Zeitpunkt ${\displaystyle t}$

${\displaystyle K}$: Basispreis, als Vertragsbestandteil festgelegt

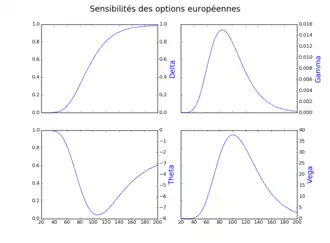
Als Griechen (englisch Greeks) werden die partiellen Ableitungen des Optionspreises nach den jeweiligen Modellparametern bezeichnet. Der Vorteil der expliziten Formel für die Optionspreise – etwa im Gegensatz zu einer numerischen Lösung – liegt darin, dass diese Ableitungen leicht berechnet werden können.

Die Griechen sind für das Risikomanagement wichtig. Sie erleichtern es dabei, den Einfluss einzelner Risikofaktoren zu analysieren. Dies gilt insbesondere auf Ebene eines Portfolios von Finanzinstrumenten, wenn der Einfluss einzelner Risikofaktoren – nämlich der Modellparameter – auf das Gesamtportfolio abgeschätzt werden soll. Ein Beispiel wäre ein Portfolio aus Optionen und Positionen im zugehörigen Basiswert, also z. B. Optionen auf den Euro-Bund-Future und Euro-Bund-Future-Positionen als solche. Über das Delta kann die (lineare) Auswirkung einer Änderung im Future-Preis auf das Gesamtportfolio dargestellt werden.

Deshalb können die Griechen auch zur Risikoabsicherung verwendet werden. Das bekannteste Beispiel ist das Delta-Hedging. Anhand der Rho-Sensitivität beispielsweise kann ermittelt werden, wie ein Optionsportfolio gegen Änderungen des Refinanzierungszinssatzes abgesichert werden muss.

Im Black-Scholes-Modell wird die Volatilität ${\displaystyle \sigma }$ als konstant angenommen. Alle ex-post-Berechnungen von Standardabweichungen der Renditen zeigen aber, dass die Volatilität über die Zeit nicht konstant ist, sondern eher ein sogenanntes Volatilitätslächeln bildet.

Eine weitere Schwäche besteht darin, dass die Volatilität als wichtigste Variable selbst prognostiziert werden muss. Das geschieht entweder mit Hilfe von Regressionsmodellen über die Extrapolation von Vergangenheitswerten oder über die Bestimmung der impliziten Volatilitäten (siehe dort), die aktuellen Marktpreisen zugrunde liegen könnten. Außerdem enthält das Modell die vereinfachende Annahme, dass Renditen normalverteilt sind. Die Normalverteilung enthält wenig Gewicht an ihren Enden, wodurch dem Auftreten von Extremereignissen zu wenig Rechnung getragen werden kann (siehe Wölbung (Statistik)).

Diese Einschränkungen des Black-Scholes-Modells zeigen sich bei den gehandelten Preisen von Optionen, wenn man die durch die Optionspreise implizierten Volatilitäten betrachtet. Die implizite Volatilität für eine Option auf einen bestimmten Basiswert ist nicht konstant, sondern ändert sich im Zeitablauf. Zudem hängt die implizite Volatilität für einen bestimmten Zeitpunkt von der Geldnähe und von der Restlaufzeit der Option (Zeitstruktur der Volatilität) ab. Beide Beobachtungen stimmen nicht mit der Modellannahme einer einheitlichen, konstanten Volatilität überein. Die Verwendung restlaufzeit- und geldnäheabhängiger impliziter Volatilitäten sind eine Methode, mit den Einschränkungen des Black-Scholes-Modells umzugehen. Würde auf dem Optionsmarkt statt der Black-Scholes-Preisformel ein anderes Modell zum Standard, ist anzunehmen, dass sich nicht die gehandelten Optionspreise ändern würden, sondern die vom Modell implizierten Volatilitäten.^[12]

Erweiterte Modelle, in denen die Volatilität als fallende Funktion vom Aktienkurs angenommen wird, wie z. B. das CEV-Modell, liefern bessere Resultate.

Originalarbeiten

• Fischer Black, Myron Scholes: The Pricing of Options and Corporate Liabilities. In: Journal of Political Economy. Band 81, Nr. 3, 1973, ISSN 0022-3808, S. 637–654, doi:10.1086/260062. 
• Robert C. Merton: Theory of Rational Option Pricing. In: The Bell Journal of Economics and Management Science. Band 4, Nr. 1, 1973, ISSN 0005-8556, S. 141–183, doi:10.2307/3003143. 

Sekundärliteratur

• Roger Lowenstein: When Genius Failed - The Long-Term Capital Managewment (LTCM). Fourth Estate / HarperCollins Publisher, London W68JB 2001. 
• Andreas Merk: Optionsbewertung in Theorie und Praxis: Theoretische und empirische Überprüfung des Black/Scholes-Modells (= SpringerLink Bücher). Gabler Verlag / Springer Fachmedien Wiesbaden GmbH, Wiesbaden, Wiesbaden 2011, ISBN 978-3-8349-2543-5. 

• Anatol Porak: Die Optionspreisformel Von Black und Scholes: Anwendungsmöglichkeiten und Grenzen (= Oikos Studien Zur Ökonomie Ser). Springer Gabler. in Springer Fachmedien Wiesbaden GmbH, Wiesbaden 1988, ISBN 978-3-409-14783-5. 
• Nasser Saber: Speculative Capital. Financial Times u. a., London 1999
  • Vol. 1: The invisible hand of global finance. ISBN 0-273-64155-7,
  • Vol. 2: The nature of risk in capital markets. ISBN 0-273-64422-X.

• Nobel-Vorlesungen 1997 von Scholes und Merton
• American Mathematical Society (Memento vom 20. April 2005 im Internet Archive) zum 97er Wirtschaftsnobelpreis, mit weiteren Links
• Bradley University mehrseitige, informelle Darstellung mit umfangreicher Bibliographie
• Excel-Makros zur Berechnung des Optionspreises

1. ↑ Üblicherweise wird in der Praxis eine Risikoprämie ${\displaystyle \mu -r>0}$ auf risikobehaftete Anlagen aufgeschlagen. Dadurch ist das Marktwahrscheinlichkeitsmaß ${\displaystyle \mathbb {P} }$ zu optimistisch; die erwarteten Preisentwicklungen sind zu hoch. Deshalb ist der Maßwechsel zum äquivalenten Martingalmaß ${\displaystyle \mathbb {P} ^{\ast }}$ vonnöten.
2. ↑ Unter ${\displaystyle \mathbb {P} ^{\ast }}$ ist ${\displaystyle W}$ ein Wiener-Prozess mit Driftterm ${\displaystyle -\theta }$. Es handelt sich um denselben Prozess, bloß durch ein anderes Maß betrachtet.
3. ↑ Alternativ mit umgekehrtem Vorzeichen: eine Longposition im Derivat und eine Shortposition in den Aktien in der angegebenen Größe. In der Praxis wird dieses Konzept der Portfolioabsicherung in Form des Delta-Hedging angewendet.
4. ↑ Hierbei sind ${\displaystyle \mu }$ und ${\displaystyle W}$ dieselben Größen wie zuvor, da der Preis des Derivats vom Preisprozess der Aktie abhängt. Der Wiener-Prozess ${\displaystyle W}$ beeinflusst also den Aktienpreis über einen Faktor ${\displaystyle \sigma \,S}$ und den Wert des Derivats über einen Faktor ${\displaystyle \sigma \,S\,{\frac {\partial V}{\partial S}}}$.

1. ↑ Korrekte Aussprache von Black-Scholes bei Merriam-Webster
2. ↑ Thomas Heimer, Sebastian Arend: The genesis of the Black-Scholes option pricing formula. Nr. 98. Frankfurt School - Working Paper Series, 2008 (econstor.eu [abgerufen am 29. November 2024]). 
3. ↑ Mehrling, Perry: „Understanding Fischer Black“ first draft of the book chapters that deal with Black's academic years „Fischer Black and the Revolutionary Idea of Finance“ (Memento vom 22. Juni 2010 im Internet Archive) (PDF; 158 kB), 2005
4. ↑ Wolfgang Hafner; Heinz Zimmermann: Ein vergessener genialer Wurf zur Bewertung von Optionen. In: Neue Zürcher Zeitung. 8. Oktober 2005, ISSN 0376-6829 (nzz.ch [abgerufen am 24. Juli 2025]). 
5. ↑ Darstellung gemäß: John C. Hull: Options, futures and other derivatives. 9. Aufl., Pearson Education, 2015, ISBN 978-0-13-345631-8, S. 331.
6. ↑ Rene Carmona und Valdo Durrleman: Generalizing the Black-Scholes Formula to Multivariate Contingent Claims. In: Journal of Computational Finance. Band 9, 2006, S. 43–67, doi:10.21314/JCF.2005.159. 
7. ↑ Lutz Kruschwitz, Maria Stefanova: Die Black-Scholes-Differentialgleichung. In: WiSt - Wirtschaftswissenschaftliches Studium. Band 36, Nr. 2, 2007, S. 82–87, doi:10.15358/0340-1650-2007-2-82 (Originalartikel oder Entwurf einer früheren Fassung [abgerufen am 3. August 2025]). 
8. ↑ Marek Musiela, Marek Rutkowski: Martingale Methods in Financial Modelling. 2. Auflage. Springer, Berlin/Heidelberg 2005, S. 107. 
9. ↑ Marek Musiela und Marek Rutkowski: Martingale Methods in Financial Mathematics. 2. Auflage. Springer, Berlin/Heidelberg, S. 96 ff. 
10. ↑ Die Herleitung in diesem Abschnitt folgt: John C. Hull: Options, futures and other derivatives. 9. Aufl., Pearson Education, 2015, ISBN 978-0-13-345631-8, S. 331 ff.
11. ↑ Lutz Hahnenstein, Sascha Wilkens, Klaus Röder: Die Black-Scholes-Optionspreisformel. In: WiSt - Wirtschaftswissenschaftliches Studium. Band 30, Nr. 7, 2001, S. 355–361, doi:10.15358/0340-1650-2001-7-355 (vahlen.de [abgerufen am 3. August 2025]). 
12. ↑ John C. Hull: Options, Futures, and Other Derivatives. 3rd edition. Prentice Hall International, Upper Saddle River NJ 1997, ISBN 0-13-264367-7, S. 503–505, 510f (Prentice-Hall International Editions).