Bergsteigeralgorithmus
Der Bergsteigeralgorithmus (engl. hill climbing) ist ein einfaches, heuristisches Optimierungsverfahren. Es besteht dabei eine Analogie zu einem Bergsteiger, der im dichten Nebel den Gipfel sucht und dazu seine Schritte möglichst steil bergauf lenkt. Geht es nach allen Richtungen nur noch nach unten, ist er auf einem Gipfel angekommen.
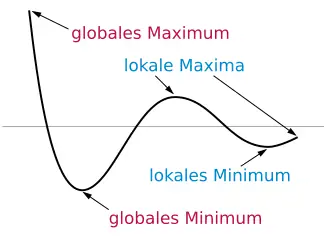
Ebenso wird im Bergsteigeralgorithmus eine potenzielle Lösung für ein gegebenes Problem Schritt für Schritt verbessert. Dabei wird jeweils eine lokale Veränderung durchgeführt und nur übernommen, wenn der entstandene Lösungskandidat besser geeignet ist. Das Verfahren endet, wenn vom aktuellen Punkt aus keine Verbesserung mehr möglich ist – analog ist der Bergsteiger auf einem Hügel angekommen. Der gefundene Punkt ist im besten Fall das globale Maximum (Bergspitze) oder nur ein lokales (Nebengipfel). Der Bergsteigeralgorithmus kann als simpler evolutionärer Algorithmus aufgefasst werden, wobei es nur ein Individuum, keine Rekombination und eine Mutations-Operation gibt.
Für das Problem der lokalen Maxima gibt es folgende Ansätze:
- Eine ganze Population von Bergsteigern beginnt an verschiedenen Startpunkten, sodass verschiedene Maxima erklommen werden.
- Ein lokales Maximum wird durch eine einmalige starke Mutation verlassen, durch abermaliges Bergsteigen kann dann ein anderes Maximum gefunden werden.
Eine ausführliche Implementierung eines Bergsteigeralgorithmus ist im Artikel Downhill-Simplex-Verfahren beschrieben.
Pseudocode-Beispiel
function HillClimbing(startNode, evaluate, generateNeighbors, maxIterations):
# INITIALISIERUNG
# besterKnoten: Speichert den global besten gefundenen Zustand während der gesamten Suche
besterKnoten = startNode
# besteBewertung: Bewertung des global besten Zustands
besteBewertung = evaluate(startNode)
# aktuellerKnoten: Der Zustand, von dem aus in dieser Iteration Nachbarn generiert werden
aktuellerKnoten = startNode
# aktuelleBewertung: Bewertung des aktuellen Zustands (zwischengespeichert zur Vermeidung wiederholter Berechnung)
aktuelleBewertung = besteBewertung
# HAUPTSUCHSCHLEIFE - Maximal maxIterations Durchläufe
for i = 1 to maxIterations:
# NACHBARGENERIERUNG
# Erzeugt alle möglichen Nachfolgezustände des aktuellen Knotens
# Die Art der Nachbarn hängt von der Problemdomäne ab (z.B. kleine Änderungen an Parametern)
nachbarn = generateNeighbors(aktuellerKnoten)
# INITIALISIERUNG DER NACHBARSUCHE
besterNachbar = NULL # Wird auf den besten gefundenen Nachbarn gesetzt
# Startwert für Vergleich - wird durch erste bessere Bewertung ersetzt
# FÜR MINIMIERUNGSPROBLEME: +INFINITY statt -INFINITY verwenden
besteNachbarBewertung = -INFINITY
# NACHBARN EVALUIEREN
# Durchläuft alle generierten Nachbarn, um den besten zu finden
for nachbar in nachbarn:
# Bewertungsfunktion berechnet die Qualität dieses Nachbarn
bewertung = evaluate(nachbar)
# VERGLEICH MIT AKTUELL BESTEM NACHBARN
# FÜR MINIMIERUNGSPROBLEME: < statt > verwenden
if bewertung > besteNachbarBewertung:
# Neuen besten Nachbarn gefunden - aktualisieren
besterNachbar = nachbar
besteNachbarBewertung = bewertung
# ABBRUCHBEDINGUNG PRÜFEN (Lokales Maximum)
# Wenn kein Nachbar besser ist als der aktuelle Zustand:
# FÜR MINIMIERUNGSPROBLEME: >= statt <= verwenden
if besteNachbarBewertung <= aktuelleBewertung:
# Abbruch, da lokales Optimum erreicht
# Kein besserer Nachbar in der Nachbarschaft existiert
break
# BEWEGUNG ZUM NEUEN ZUSTAND
# Wechsel zum besten gefundenen Nachbarn
aktuellerKnoten = besterNachbar
# Bewertung des neuen Zustands speichern (bereits in der Schleife berechnet)
aktuelleBewertung = besteNachbarBewertung
# GLOBALE BESTWERT-AKTUALISIERUNG
# Prüft, ob der neue Zustand besser ist als der bisher global beste
# FÜR MINIMIERUNGSPROBLEME: < statt > verwenden
if aktuelleBewertung > besteBewertung:
# Neuer global bester Zustand gefunden
besterKnoten = aktuellerKnoten
besteBewertung = aktuelleBewertung
# ERGEBNISRÜCKABE
# Gibt den besten während der gesamten Suche gefundenen Zustand zurück
# Dieser kann vom aktuellen Zustand abweichen (z.B. wenn später Pfade schlechter waren)
return besterKnoten
Fragestellungen
Schrittweite
Existiert eine Abstandsfunktion auf der Definitionsmenge D einer Funktion, so stellt sich oft die Frage, wie groß einer der Schritte (von einer Stelle zur nächsten) sein soll, zum Beispiel:
- immer gleich groß (gleicher Abstand in D)
- zufällig groß (wird angewendet zur Vermeidung des Festlaufens in lokalen Extrema)
- kleiner werdend (wenn der Algorithmus erkennt, dass das Optimum in der Nähe sein muss und sich auf dieses konzentrieren muss, z. B. relativ zur Gradientennorm)
- größer werdend (wenn die Richtung erfolgversprechend erscheint)
- abhängig vom Individuum
Selektionsstrategie
Wann soll die Selektion auf einzelne Bergsteiger angewandt werden?
- nach jedem Schritt
- nach jedem Bergauf-Schritt
- wenn ein lokales Maximum erreicht wurde
- erst nach größeren Zeiträumen (um das Überwinden von „Durststrecken“ zu ermöglichen)
Individuenanzahl
Wie viele Individuen sollen verwendet werden, um eine gute Lösung zu erreichen?
Abbruchkriterium
Wie viele Generationen soll es geben, bis die Suche nach besseren Lösungen aufgegeben wird?
Literatur
- Stuart Russel, Peter Norvig: Artificial Intelligence: A Modern Approach. Third Edition. Prentice Hall, Upper Saddle River, NJ 2010, ISBN 978-0-13-604259-4, S. 122–125.