Bass-Serre-Baum

Bass-Serre-Bäume sind eine Konstruktion aus dem mathematischen Teilgebiet der Gruppentheorie, mit der Gruppenwirkungen von amalgamierten Produkten oder allgemeiner Fundamentalgruppen von Graphen von Gruppen auf Bäumen konstruiert werden können.

Sie sind nach Hyman Bass und Jean-Pierre Serre benannt.

Es sei ${\displaystyle (E,K,\left\{G_{e}\right\}_{e\in E},\left\{G_{k}\right\}_{k\in K},\left\{\alpha _{k,i}\colon G_{k}\to G_{e_{i}}\right\}_{k=(e_{0},e_{1})\in K,i=0,1})}$ ein Graph von Gruppen und ${\displaystyle G}$ seine Fundamentalgruppe. Der zugehörige Bass-Serre-Baum ${\displaystyle T}$ wird konstruiert wie folgt:

• die Ecken sind ${\displaystyle \bigsqcup _{e\in E}G/G_{e}}$
• die Kanten sind ${\displaystyle \bigsqcup _{k\in K}G/G_{k}}$
• die Kante ${\displaystyle \left[g\right]\in G/G_{k}}$ hat die Ecken ${\displaystyle \left[g\right]\in G/G_{e_{0}}}$ und ${\displaystyle \left[gk\right]\in G/G_{e_{1}}}$, für ${\displaystyle k=(e_{0},e_{1})\in K}$

Die Gruppe ${\displaystyle G}$ wirkt auf ${\displaystyle T}$ durch Linksmultiplikationen auf ${\displaystyle G/G_{e}}$ und ${\displaystyle G/G_{k}}$.

${\displaystyle T}$ ist ein Baum.^[1]

Es sei ${\displaystyle (E,K,\left\{G_{e}\right\}_{e\in E},\left\{G_{k}\right\}_{k\in K},\left\{\alpha _{k,i}\colon G_{k}\to G_{e_{i}}\right\}_{k=(e_{0},e_{1})\in K,i=0,1})}$ ein Graph von Gruppen und ${\displaystyle T}$ sein Bass-Serre-Baum. Dann sind die Stabilisatoren von Ecken ${\displaystyle {\tilde {e}}}$ bzw. Kanten ${\displaystyle {\tilde {k}}}$ isomorph zu ${\displaystyle G_{e}}$ bzw. ${\displaystyle G_{k}}$ für ${\displaystyle e=\left[{\tilde {e}}\right]}$ bzw. ${\displaystyle k=\left[{\tilde {k}}\right]}$ und der Quotient ${\displaystyle G\backslash T}$ ist der dem Graph von Gruppen unterliegende Graph ${\displaystyle (E,K)}$.

Die beiden folgenden Graphen^[2] sind die Bass-Serre-Bäume eines freien Produkts bzw. einer HNN-Erweiterung.

• Bass-Serre-Baum des freien Produkts ${\displaystyle \mathbb {Z} /2\mathbb {Z} *\mathbb {Z} /3\mathbb {Z} \simeq PSL(2,\mathbb {Z} )}$:

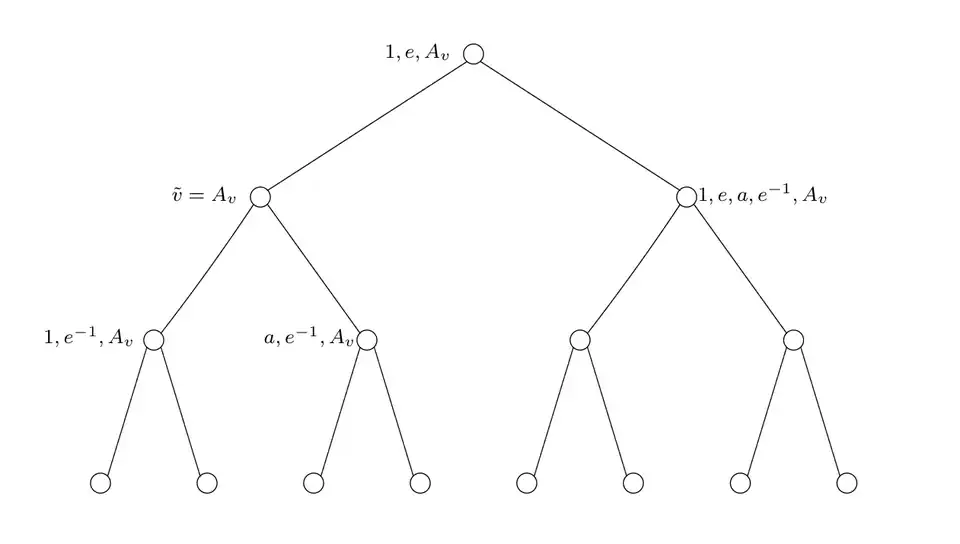
• Bass-Serre-Baum der Baumslag-Solitar-Gruppe ${\displaystyle BS(1,2)=\langle a,t\colon tat^{-1}=a^{2}\rangle }$:

Jean-Pierre Serre: Trees. Translated from the French original by John Stillwell. Corrected 2nd printing of the 1980 English translation. Springer Monographs in Mathematics. Springer-Verlag, Berlin, 2003. ISBN 3-540-44237-5

Richard Weidmann: Bass-Serre theory (Memento vom 19. Februar 2015 im Internet Archive)

1. ↑ Serre, op.cit., Theorem 12 in Chapter I
2. ↑ Weidmann, op.cit., Chapter 5