Elliptische Modulform

Elliptische Modulformen umfassen in der Mathematik eine bestimmte Gattung von Funktionen, die eine überaus starke Form der Symmetrie besitzen, und aufgrund ihrer sehr breiten Anwendungsmöglichkeiten wie zum Beispiel in algebraischer, algorithmischer und analytischer Zahlentheorie, Topologie, Darstellungstheorie, Gruppentheorie, komplexer, algebraischer bzw. arithmetischer Geometrie, diskreter Mathematik, Kombinatorik, Funktionentheorie, Stringtheorie, Quantenphysik, Differentialgleichungen und Knotentheorie zu den bedeutendsten Objekten innerhalb der modernen Mathematik bzw. theoretischen Physik gehören. Das Wort „elliptisch“ bedeutet in diesem Kontext, dass die betreffenden Modulformen auf Modulräumen elliptischer Kurven definiert sind. Hierbei ist „Modul“ ein altmodisches Wort für „Parameter, der für ein geometrisches Objekt steht“. In der Literatur wird jedoch dieser Zusatz häufig weggelassen, wenn aus dem Kontext ersichtlich ist, um welchen Typ Modulform es sich handelt.

Elliptische Modulformen – und ihre Verallgemeinerungen – werden als Kandidaten für eine Zusammenführung einiger Teilbereiche der Mathematik und theoretischen Physik gesehen. Damit ist gemeint, dass sie Brücken zwischen mathematischen aber auch physikalischen Theorien bauen, die längere Zeit als verschieden angesehen wurden und teils eine völlig unterschiedliche mathematische Historie und Tradition haben. In manchen Fällen sind solche Zusammenhänge in der Vergangenheit schon gezeigt worden, in anderen Fällen, besonders im Umfeld der Zahlentheorie und Darstellungstheorie, werden sie im Rahmen des Langlands-Programms bis heute nur vermutet. Sehr kurz beschreiben lassen sich diese Zusammenhänge durch ein „gemeinsames Vorhandensein von Symmetrie“. Vereinheitlichende mathematische Theorien sind deshalb von Interesse, da sie gewissermaßen die tiefere „Architektur der Mathematik“ aufzeigen, und durch die dadurch entstehenden Einsichten neue Anwendungsmöglichkeiten schaffen können. In etwa eröffnet sich die Möglichkeiten, Probleme einer Theorie äquivalent in eine andere Theorie zu übertragen, und gegebenenfalls mit den dort vorhandenen Methoden zu lösen. Auch in der theoretischen Physik gelten Modulformen als Bestandteil innerhalb mathematischer Theorien, die tiefere Strukturen hinter dem Aufbau des Universums erklären könnten – etwa im Umfeld der Stringtheorie – ähnlich wie die Riemannsche Geometrie aus der Mathematik die Grundlage für Albert Einsteins Relativitätstheorie bildete, die sich später experimentell bestätigen ließ.

Die Theorie der elliptischen Modulformen ist enorm umfangreich und bis heute Gegenstand intensiver Forschung. Zwei der sieben Millennium-Probleme der Mathematik – die Riemannsche Vermutung und die Vermutung von Birch und Swinnerton-Dyer – treffen Aussagen über Objekte – sog. L-Funktionen –, die unmittelbar mit elliptischen Modulformen verknüpft sind. Etwa besagt die Riemannsche Vermutung, dass sämtliche nichttriviale Nullstellen der Riemannschen Zetafunktion auf einer gemeinsamen Geraden liegen – und damit die Primzahlen ein „möglichst zufälliges“ Verteilungsmuster aufweisen. Diese Gerade ist eine Spiegelungsgerade für die Werte der Zetafunktion – und diese Symmetrie rührt von einer Modulform her, die mit der Zetafunktion assoziiert ist. Zahlreiche hohe Mathematikpreise wurden für Arbeiten im Bereich der Modulformen vergeben, etwa an Andrew Wiles, Pierre Deligne, Richard Borcherds, Jean-Pierre Serre, Laurent Lafforgue, Ngô Bảo Châu, Richard Taylor, Maryna Viazovska, Dennis Gaitsgory und Kathrin Bringmann.

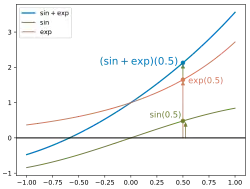
Um das Konzept einer elliptischen Modulform zu verstehen, kann es helfen, die trigonometrischen Funktionen, wie Sinus und Kosinus, als eine „Vorstufe“ zu sehen. Hier äußert sich die Symmetrie durch deren Periodizität und dem Spiegelungsverhalten an den Achsen bei gleichzeitiger Holomorphie (wenn auf komplexe Zahlen fortgesetzt). Im Falle der Modulformen kommen jedoch neben der Periodizität noch eine unendliche Anzahl weiterer Funktionalgleichungen hinzu, was ihnen erheblich mehr Struktur verleiht. Im einfachsten Falle spricht man bei einer holomorphen Funktion

${\displaystyle f\colon \mathbb {H} \to \mathbb {C} }$ (als Funktion auf der oberen Halbebene ${\displaystyle \mathbb {H} }$ der komplexen Zahlen)

von einer ganzen, elliptischen Modulform des Gewichts ${\displaystyle k\in \mathbb {Z} }$ zur vollen Modulgruppe, wenn zwei Bedingungen erfüllt sind:

1. Funktionalgleichungen: ${\displaystyle (cz+d)^{-k}f\left({\frac {az+b}{cz+d}}\right)=f(z)}$ für alle ganzen Zahlen ${\displaystyle a,b,c,d}$ mit ${\displaystyle ad-bc=1}$ und alle ${\displaystyle z\in \mathbb {H} }$,
2. Wachstumsbedingung: ${\displaystyle \lim _{\mathrm {Im} (z)\to \infty }f(z)}$ existiert (mit dem Imaginärteil ${\displaystyle \mathrm {Im} (z)}$).

Durch die Wahl ${\displaystyle a=b=d=1}$ und ${\displaystyle c=0}$ ergibt sich

${\displaystyle f(z+1)=f(z)}$,

weshalb jede Modulform eine periodische Funktion ist. Als solche kann sie, wegen ihrer Holomorphie, in eine Fourier-Reihe entwickelt werden:

${\displaystyle f(z)=\sum _{n=-\infty }^{\infty }a_{n}(f)e^{2\pi inz}}$,

wobei die Wachstumsbedingung äquivalent zu ${\displaystyle a_{n}(f)=0}$ für alle ${\displaystyle n<0}$ ist. Die Fourier-Koeffizienten tragen oft wichtige, zahlentheoretische Informationen. Zu den einfachsten Beispielen von Modulformen gehören die Eisensteinreihen.

Etwas allgemeiner handelt es sich bei elliptischen Modulformen um auf der oberen Halbebene meromorphe Funktionen, die oberes Transformationsverhalten bezüglich ihrer Funktionswerte respektieren, und am Rand ihres Definitionsbereichs kein zu starkes Wachstum besitzen. Wichtiger Spezialfall ist der Begriff der Modulfunktion, der zum Gewicht ${\displaystyle k=0}$ korrespondiert und damit zusätzlich eine Form der absoluten Invarianz fordert, was eine höhere Anforderung als denen einer Modulform darstellt.

Als eine besonders prominente Anwendung der Theorie der elliptischen Modulformen gilt der Beweis des Großen Fermatschen Satzes aus der Zahlentheorie, der besagt, dass die Gleichung

${\displaystyle x^{n}+y^{n}=z^{n}}$

mit ${\displaystyle n\geq 3}$ für keine natürlichen Zahlen ${\displaystyle x,y,z}$ lösbar ist. Das bedeutet beispielsweise, dass eine positive Kubikzahl niemals in zwei positive Kubikzahlen zerfällt, weshalb es zum Beispiel niemals eine Gleichheit etwa zwischen

${\displaystyle 15\cdot 15\cdot 15+19\cdot 19\cdot 19}$ und ${\displaystyle 21\cdot 21\cdot 21}$

geben kann. Allerdings gilt der Beweis dieser Aussage als äußerst schwierig. Weitere Anwendungen betreffen die Theorie der schwarzen Löcher aus der Physik, aber auch schnelle Methoden zur Berechnung vieler Dezimalstellen der Kreiszahl ${\displaystyle \pi =3,141\ldots }$.

Die Entdeckungsgeschichte der Modulformen lässt bis in die Anfänge des 19. Jahrhunderts zurückverfolgen, wo sie besonders mit Namen wie Carl Friedrich Gauß, Gotthold Eisenstein und Carl Gustav Jacobi assoziiert sind. Umfangreiche Forschungsprogramme ab dem 20. Jahrhundert haben jedoch zu sehr weitreichenden Verallgemeinerungen von „klassischen Modulformen“ geführt, und den Begriff der automorphen Formen geprägt, die in der modernen Mathematik primär als Objekte der Darstellungstheorie gesehen werden.

Neben den elliptischen Modulformen wurden viele weitere Arten von Modulformen gefunden, zum Beispiel Jacobiformen, Siegelsche Modulformen, Hilbertsche Modulformen sowie p-adische Modulformen.

Dieser Artikel geht hinsichtlich der mathematischen Details primär auf die Standardsituation der vollen Modulgruppe ein, beleuchtet die Bedeutung der elliptischen Modulformen jedoch im Kontext sämtlicher Kongruenzuntergruppen. Für die mathematischen Details dieser Verallgemeinerung wird auf den Artikel Elliptische Modulformen zu Kongruenzuntergruppen verwiesen.

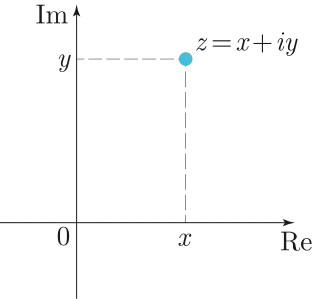
Komplexe Zahlen erweitern den Bereich der reellen Zahlen durch Hinzunehmen sog. imaginärer Zahlen. Diese sollen die Eigenschaft haben, algebraische Gleichungen zu lösen, die im Reellen nicht lösbar sind. Ein Beispiel ist die quadratische Gleichung ${\displaystyle x^{2}+1=0}$. Sie hat keine reelle Lösung, da das Quadrat einer reellen Zahl stets nicht-negativ ist. Fügt man jedoch den reellen Zahlen eine imaginäre Zahl ${\displaystyle i}$ mit der Eigenschaft ${\displaystyle i^{2}=-1}$ hinzu, so kann die obige Gleichung gelöst werden.

Während die reellen Zahlen eine Zahlengerade aufspannen, breiten die komplexen Zahlen eine Ebene aus. Jede komplexe Zahl ${\displaystyle z}$ ist von der Form ${\displaystyle z=x+iy}$ mit reellen Zahlen ${\displaystyle x}$ und ${\displaystyle y}$. Geht man ${\displaystyle x}$ Schritte in „reelle Richtung“ und ${\displaystyle y}$ Schritte in „imaginäre Richtung“, so wird die komplexe Zahl ${\displaystyle x+iy}$ mit dem Punkt ${\displaystyle (x,y)}$ in der Euklidischen Ebene identifiziert. Dabei wird ${\displaystyle x}$ als Realteil und ${\displaystyle y}$ als Imaginärteil von ${\displaystyle z}$ bezeichnet.

Eine wichtige Eigenschaft komplexer Zahlen ist, dass man mit ihnen, wie im Falle der reellen Zahlen, rechnen kann. Damit ist gemeint, dass Plus, Minus, Mal und Geteilt auch für komplexe Zahlen definiert ist. Um dies umzusetzen, ist lediglich das Beherrschen der reellen Rechenregeln sowie die Regel ${\displaystyle i^{2}=-1}$ vonnöten. Die Addition wird in Real- und Imaginärteil separat ausgeführt, also zum Beispiel ${\displaystyle (-3+2i)+(4+10i)=1+12i}$, und beim Multiplizieren müssen die Klammern verrechnet werden:

${\displaystyle (a+bi)(c+di)=(ac-bd)+(ad+bc)i.}$

Dabei entsteht der Term ${\displaystyle -bd}$ beim Ausmultiplizieren aus dem Produkt ${\displaystyle bidi}$. Auch die Division ist möglich, etwa dadurch, den Nenner durch passendes Erweitern und die dritte binomische Formel reell zu machen:

${\displaystyle {\frac {1+i}{1-2i}}={\frac {(1+i)(1+2i)}{(1-2i)(1+2i)}}={\frac {-1+3i}{5}}=-{\frac {1}{5}}+{\frac {3}{5}}i.}$

Somit bilden auch die komplexen Zahlen eine Zahlenstruktur, in der algebraisch gerechnet werden kann. Man sagt auch, dass die Menge der komplexen Zahlen ${\displaystyle \mathbb {C} }$, genau wie die reellen Zahlen ${\displaystyle \mathbb {R} }$, einen Körper bilden.

Besonders wichtig in der Theorie der Modulformen ist die obere Halbebene der komplexe Zahlen. Dabei handelt es sich um jene komplexe Zahlen, deren Imaginärteil positiv ist. Abgekürzt wird dies in der Literatur häufig mit ${\displaystyle \mathbb {H} }$^[1] (aber auch ${\displaystyle {\mathfrak {H}}}$^[2] und ${\displaystyle {\mathfrak {h}}}$^[3] sind gängige Notationen). In Formeln schreibt man

${\displaystyle \mathbb {H} :=\{z\in \mathbb {C} \,\,\colon \,\,\mathrm {Im} (z)>0\}.}$

Beispielsweise ist ${\displaystyle 1+i\in \mathbb {H} }$, aber ${\displaystyle 2-3i\notin \mathbb {H} }$. Die obere Halbebene ist der Definitionsbereich von Modulformen als Funktionen.

Eine mathematische Funktion stellt ganz allgemein eine Beziehung zwischen zwei Mengen ${\displaystyle M}$ und ${\displaystyle N}$ über eine Abbildungsvorschrift her. Funktionen ${\displaystyle f\colon M\rightarrow N}$ müssen die Regel erfüllen, dass jedem Element aus ${\displaystyle M}$ genau ein Element in ${\displaystyle N}$ zugeordnet wird.

Einige Beispiele reeller Funktionen lassen sich direkt auf die komplexen Zahlen übertragen. Dazu zählt etwa die quadratische Funktion ${\displaystyle f(z)=z^{2}}$.

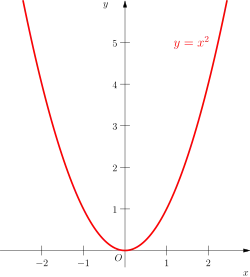
Reelle Funktionen induzieren „Tabellendaten“ der Form ${\displaystyle (x,f(x))}$, wobei die Eingabewerte ${\displaystyle x}$ den Definitionsbereich von ${\displaystyle f}$ durchlaufen. Die Analogie zu einer Tabelle entsteht dadurch, dass Daten ${\displaystyle x}$ und ${\displaystyle f(x)}$ in Zeilen- oder Spaltenform zusammengestellt werden können. Es ist jedoch nicht möglich, alle Werte einer reellen Funktion in eine Tabelle einzutragen, da es zum Beispiel bereits nicht möglich ist, alle Werte ${\displaystyle 0<x<1}$ aufzulisten. Alle nicht leeren, echten Intervalle der reellen Zahlen sind überabzählbar. Daher ist die Darstellung einer reellen Funktion anhand eines Schaubildes üblich. Dabei macht man sich zunutze, dass der Definitionsbereich ein Teil eines Zahlenstrahles ist, ebenso der Wertebereich. Ergo sammeln sich die Informationen ${\displaystyle (x,f(x))}$ zu Punkten ${\displaystyle (x,y)}$ in einer zweidimensionalen Ebene. Hebt man diese in der Ebene hervor, bekommt man einen Überblick über das Verhalten einer reellen Funktion.

Für komplexe Funktionen ist die Situation anders. Hier ist bereits der Eingangsbereich eine Fläche. Von daher müsste ein Schaubild nach Art reeller Funktionen vierdimensional sein, was nicht verständlich darstellbar ist.^[4] Ein Weg, komplexe, insbesondere holomorphe, Funktionen darzustellen, bedient sich eines Farbschlüssels. Einer komplexen Zahl wird je nach „Himmelsrichtung“ eine Farbe zugeordnet, wobei der Ursprung, also die Null, den Orientierungspunkt bildet. Zusätzlich wird mit der Helligkeit des Farbtons die Größe im Sinne des Abstands zum Ursprung visualisiert. Dabei bedeutet „dunkel“ nahe bei Null, und „hell“ nahe bei „Unendlich“.

• 
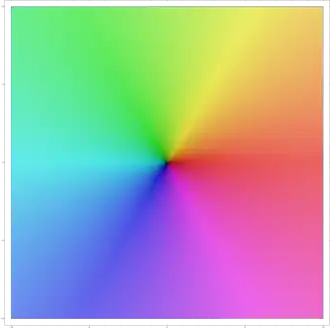  Der Farbschlüssel, gezeigt durch das Schaubild der Selbstabbildung ${\displaystyle z\mapsto z}$. In etwa stehen rötliche Farben für komplexe Zahlen, die annähernd positiv reell sind.
• 
  Schaubild der komplexen Quadratfunktion ${\displaystyle z\mapsto z^{2}}$. Im Zentrum ist ihr Wert Null (schwarzer Punkt), denn ${\displaystyle 0^{2}=0}$. Von dort aus nimmt sie links und rechts, also auf der reellen Achse, rote Werte (siehe linken Farbschlüssel) an, denn Quadrate reeller Zahlen sind nie negativ. Von der Mitte startend nach Nord oder Süd ist Türkis präsent: Die Quadrate rein imaginärer Zahlen sind negativ.
• 
  Die komplexe Fortsetzung der Exponentialfunktion ${\displaystyle z\mapsto e^{z}}$. Ihre Beträge werden mit wachsendem Realteil schnell größer (exponentielles Wachstum), das Schaubild also heller, und für fallende Realteile kleiner, das Schaubild also dunkler. Parallel zur imaginären Achse des Eingabebereichs ist sie eine periodische Funktion.
• 
  Auch beim komplexen Sinus ist die Periodizität gut zu erkennen – dieses mal in reeller Ausrichtung, da ${\displaystyle \sin(z+2\pi )=\sin(z)}$. Seine Nullstellen an den Vielfachen der Kreiszahl ${\displaystyle \pi }$ sind durch die schwarzen Punkte zu erkennen.

Nicht alle komplexen Funktionen sind auf der gesamten komplexen Ebene definiert. In etwa sind Modulformen nur auf der oberen Halbebene ${\displaystyle \mathbb {H} }$ der komplexen Zahlen erklärt. Dort nehmen sie wieder komplexe Wert an. Ist also ${\displaystyle f\colon \mathbb {H} \to \mathbb {C} }$ eine Modulform, so machen die Auswertungen ${\displaystyle f(1+i)}$ und ${\displaystyle f(-3+4i)}$ Sinn, nicht aber ${\displaystyle f(-i)}$.

Gruppen wurden in der Mathematik eingeführt, um das Rechnen mit Zahlen zu verallgemeinern. Bei einer Gruppe ${\displaystyle G}$ handelt es sich um eine Menge von Objekten, zum Beispiel die ganzen Zahlen

${\displaystyle \{\ldots ,-3,-2,-1,0,1,2,3,4,\ldots \}}$

und eine Verknüpfung auf dieser Menge, sodass gewisse Eigenschaften erfüllt sind. Mit Verknüpfung ist gemeint, dass man aus je zwei Elementen der Menge ein neues Element derselben erzeugen kann. Abstrakt handelt es sich also um eine Abbildung

${\displaystyle \star \;\colon \;G\times G\longrightarrow G}$

die einem Paar ${\displaystyle (g_{1},g_{2})}$ bestehend aus zwei Gruppenelementen ein neues Gruppenelement ${\displaystyle g_{1}\star g_{2}}$ zuordnet. Im Falle der ganzen Zahlen ist eine solche zum Beispiel die Addition: Die Summe zweier ganzer Zahlen ist wiederum eine ganze Zahl. Also hat man:

${\displaystyle +\;\colon \;\mathbb {Z} \times \mathbb {Z} \longrightarrow \mathbb {Z} ,\;\;(n_{1},n_{2})\mapsto n_{1}+n_{2}.}$

Etwa gilt

${\displaystyle (2,3)\mapsto 5,\qquad (-4,3)\mapsto -1.}$

Um wirklich von einer Gruppe ${\displaystyle G}$ mit Verknüpfung ${\displaystyle \star }$ zu sprechen, muss zudem gelten:^[5]

• Assoziativgesetz: Die Klammerung bei der Verknüpfung ist egal. Zum Beispiel gilt ${\displaystyle (a\star b)\star c=a\star (b\star c)}$ für alle ${\displaystyle a,b,c\in G}$. Es ist also unerheblich, welche Verknüpfung in einer Kette von solchen zuerst ausgeführt wird, solange die Reihenfolge der Elemente nicht verändert wird. Dies ist offenbar bei der Addition in den ganzen Zahlen erfüllt, etwa gilt ${\displaystyle 2+(1+4)=(2+1)+4=7}$.
• Existenz eines neutralen Elements: Es existiert ein Element ${\displaystyle e\in G}$, das bei Verknüpfung mit einem beliebigen anderen Element dieses unverändert lässt. Es gilt also ${\displaystyle a\star e=e\star a=a}$ für alle Elemente ${\displaystyle a\in G}$. In obigem Beispiel ist das neutrale Element die Null, denn es gilt ${\displaystyle 3+0=3}$ und allgemein ${\displaystyle n+0=n}$ für jede (ganze) Zahl ${\displaystyle n}$.
• Existenz des Inversen: Zu jedem Element ${\displaystyle a\in G}$ gibt es ein Inverses, allgemein bezeichnet mit ${\displaystyle a^{-1}\in G}$, sodass ${\displaystyle a\star a^{-1}=a^{-1}\star a=e}$ gilt, also unter Verknüpfung das neutrale Element herauskommt. In obigem Beispiel der ganzen Zahlen ist ${\displaystyle -n}$ das Inverse zu ${\displaystyle n}$, da stets ${\displaystyle n-n=0}$ gilt.

Es gibt unter den Gruppen auch solche, die mit Zusatzeigenschaften auffallen.

• Gilt zusätzlich zu den Gruppeneigenschaften noch das Kommutativgesetz, also ${\displaystyle a\star b=b\star a}$ für alle ${\displaystyle a,b\in G}$, so spricht man auch von einer abelschen Gruppe (zu Ehren von Niels Henrik Abel). Zum Beispiel ist ${\displaystyle \mathbb {Z} }$ eine abelsche Gruppe, da die Summe zweier Zahlen nach deren Vertauschung unverändert bleibt.

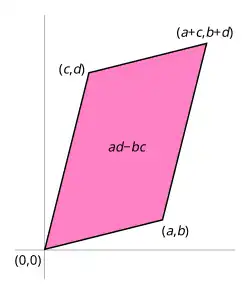
Es gibt zahlreiche Beispiele für Gruppen, etwa die Menge der rationalen Zahlen ohne die Null, in Zeichen ${\displaystyle \mathbb {Q} \setminus \{0\}}$, mit der Multiplikation als Verknüpfung (das neutrale Element ist dann die ${\displaystyle 1}$). Für die Theorie der Modulformen wichtig ist jedoch eine ganz bestimmte Gruppe, die spezielle lineare Gruppe über den ganzen Zahlen (im Falle ${\displaystyle n=2}$) – kurz ${\displaystyle \mathrm {SL} _{2}(\mathbb {Z} )}$. Genannt wird diese auch einfach volle Modulgruppe. Diese besteht aus ${\displaystyle 2\times 2}$-Matrizen mit ganzen Einträgen, deren Determinante gleich 1 ist. Einfach gesprochen handelt es sich dabei um Tabellen mit vier ganzen Einträgen, also zum Beispiel

${\displaystyle {\begin{pmatrix}2&-3\\-3&5\end{pmatrix}}.}$

Für eine allgemeine ${\displaystyle 2\times 2}$-Matrix

${\displaystyle A={\begin{pmatrix}a&b\\c&d\end{pmatrix}}}$

besagt die Bedingung Determinante = 1 aber noch zusätzlich

${\displaystyle \det(A)=ad-bc=1.}$

Obere Beispielmatrix liegt daher in ${\displaystyle \mathrm {SL} _{2}(\mathbb {Z} )}$, denn alle Einträge sind ganzzahlig und es gilt

${\displaystyle 2\cdot 5-(-3)\cdot (-3)=10-9=1.}$

Neben der komponentenweisen Addition für Matrizen, wie

${\displaystyle {\begin{pmatrix}2&-3\\-3&5\end{pmatrix}}+{\begin{pmatrix}5&0\\1&3\end{pmatrix}}={\begin{pmatrix}7&-3\\-2&8\end{pmatrix}}}$

unter derer ${\displaystyle \mathrm {SL} _{2}(\mathbb {Z} )}$ jedoch nicht zur Gruppe wird, existiert noch die Matrizenmultiplikation, in allgemeinen Symbolen:

${\displaystyle {\begin{pmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{pmatrix}}\cdot {\begin{pmatrix}b_{11}&b_{12}\\b_{21}&b_{22}\end{pmatrix}}:={\begin{pmatrix}a_{11}b_{11}+a_{12}b_{21}&a_{11}b_{12}+a_{12}b_{22}\\a_{21}b_{11}+a_{22}b_{21}&a_{21}b_{12}+a_{22}b_{22}\end{pmatrix}},}$

und wie üblich bedeutet ${\displaystyle ab}$ das gleiche wie ${\displaystyle a\cdot b}$. Unter dieser wird wegen der Rechenregel ${\displaystyle \det(AB)=\det(A)\det(B)}$ und ${\displaystyle 1\cdot 1=1}$ die Menge ${\displaystyle \mathrm {SL} _{2}(\mathbb {Z} )}$ zu einer (nicht-abelschen) Gruppe, da jede Matrix mit Determinante 1 auch eine Inverse (über ihrem Ring, in diesem Falle ${\displaystyle \mathbb {Z} }$) besitzt. Das neutrale Element der vollen Modulgruppe ist die Einheitsmatrix

${\displaystyle I_{2}:={\begin{pmatrix}1&0\\0&1\end{pmatrix}}.}$

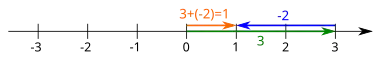
Das Konzept der Gruppenoperation (manchmal auch Gruppenwirkung) sieht vor, dass die Elemente einer Gruppe ${\displaystyle G}$ auf die Elemente einer Menge ${\displaystyle X}$ „zugreifen“, und diese „untereinander manipulieren“. Kurz gesagt wird jedes Gruppenelement ${\displaystyle g\in G}$ zu einer 1:1-Abbildung ${\displaystyle g\colon X\to X}$, man hat also eine Zuweisung

${\displaystyle G\longrightarrow \{f\colon X\to X\},}$

und dieses Prozedere ist „verträglich“ mit der Gruppenstruktur.

Anschaulich machen lässt sich dies an einem Beispiel. Gewählt wird ${\displaystyle X=\mathbb {R} }$ (die reellen Zahlen) und ${\displaystyle G=\mathbb {Z} }$ mit der Addition. Jede ganze Zahl ${\displaystyle n}$ induziert nun eine 1:1-Abbildung ${\displaystyle \mathbb {R} \to \mathbb {R} }$ via

${\displaystyle n(x):=x+n}$.

Damit wird jede ganze Zahl zu einer Funktion ${\displaystyle \mathbb {R} \to \mathbb {R} }$. Zum Beispiel gilt

${\displaystyle 2(x)=x+2,\qquad {\text{etwa}}\qquad 2(0,5)=2+0,5=2,5,\qquad {\text{oder}}\qquad (-4)(1,2)=-2,8.}$

Jede dieser Abbildungen ist 1:1, kann ${\displaystyle n(x)}$ doch sofort mit ${\displaystyle (-n)(x)}$ wieder umgekehrt werden.

Entscheidend ist die Verträglichkeit zwischen Verkettung und Gruppenstruktur: Ist allgemein ${\displaystyle g_{1},g_{2}\in G}$ und ${\displaystyle e}$ das neutrale Element, so soll für alle Elemente in ${\displaystyle X}$ immer gelten:^[6]

${\displaystyle g_{1}(g_{2}(x))=(g_{1}*g_{2})(x),\qquad {\text{sowie}}\qquad e(x)=x.}$

Es ist also ${\displaystyle e(x)}$ die triviale Abbildung, die jedes Element auf sich selbst schickt, und zudem egal, ob zwei Funktionen verkettet werden, oder stattdessen ihre Verknüpfung in ${\displaystyle G}$ gebildet wird, und die resultierende Funktion ${\displaystyle g_{1}*g_{2}\colon X\to X}$ auf ${\displaystyle x}$ angewendet. Im Falle des Beispiels liegen diese Bedingungen auf der Hand, für ganze Zahlen ${\displaystyle n_{1},n_{2}}$ und eine reelle Zahl ${\displaystyle x}$ gilt:

${\displaystyle \underbrace {n_{1}(n_{2}(x))} _{\text{Verkettung}}=n_{1}(x+n_{2})=x+n_{1}+n_{2}=\underbrace {(n_{1}+n_{2})} _{\text{Verknüpfung}}(x)\qquad {\text{und}}\qquad 0(x)=x+0=x.}$

Zum Beispiel ist ${\displaystyle 2(5(x))=2(x+5)=x+5+2=(2+5)(x)=7(x)}$.

Im Falle der Modulformen wird die Gruppenoperation der Gruppe ${\displaystyle \mathrm {SL} _{2}(\mathbb {Z} )}$ auf der oberen Halbebene ${\displaystyle \mathbb {H} }$ der komplexen Zahlen benötigt. Diese ist gegeben durch sog. Möbiustransformation. Eine Matrix

${\displaystyle A={\begin{pmatrix}a&b\\c&d\end{pmatrix}}\in \mathrm {SL} _{2}(\mathbb {Z} )}$

wird zu einer Funktion ${\displaystyle \mathbb {H} \to \mathbb {H} }$ via^[2]

${\displaystyle A(z)={\begin{pmatrix}a&b\\c&d\end{pmatrix}}(z):={\frac {az+b}{cz+d}}.}$

Dabei handelt es sich um eine linear-gebrochene Funktion. Es kann elementar – wenn auch aufwendig – nachgerechnet werden (Bruchrechnung), dass dies eine Gruppenoperation bildet. Wichtig ist dabei auch die Wohldefiniertheit, also dass die Funktionen tatsächlich ${\displaystyle \mathbb {H} \to \mathbb {H} }$ abbilden. Es gilt allerdings für Matrizen aus ${\displaystyle \mathrm {SL} _{2}(\mathbb {Z} )}$^[2]

${\displaystyle \mathrm {Im} \left({\frac {az+b}{cz+d}}\right)={\frac {\mathrm {Im} (z)}{|cz+d|^{2}}}>0\iff z\in \mathbb {H} .}$

Orbiträume einer Gruppenwirkung entstehen dann, wenn man Elemente, die unter der Operation auseinander hervorgehen, als gleich ansieht. Wieder kann als Beispiel ${\displaystyle X=\mathbb {R} }$ und ${\displaystyle G=\mathbb {Z} }$ dienen. In diesem Falle wären ${\displaystyle 0,5}$ und ${\displaystyle 3,5}$ „gleich“, da sie durch die Gruppenoperation auseinander hervorgehen:

${\displaystyle 3(0,5)=3,5.}$

Man schreibt in diesem Falle auch ${\displaystyle [0,5]=[3,5]}$, wobei die ${\displaystyle [x]}$ Äquivalenzklassen sind, sog. Bahnen. Ausgeschrieben gilt

${\displaystyle [0,5]=\{\ldots ,-1,5;-0,5;0,5;1,5;2,5;\ldots \}.}$

Im Alltag ließe sich das Prinzip der Äquivalenzklassen damit vergleichen, dass eine Person, die nur an der Anzahl an Wohnungen in einer Stadt interessiert ist, die Bewohner derselben Wohnung als „gleich“ ansehen würde, um die „Klassen an Menschen“ = Wohnungen zu zählen (wobei hier vereinfachend angenommen wird, jeder Mensch bewohne nur genau eine Wohnung). In diesem Sinne wären ${\displaystyle 0,5}$ und ${\displaystyle 1,5}$ Teil derselben Klasse bzw. „Wohnung“, da sie aus einer Translation um 1 auseinander hervorgehen, also beide in ${\displaystyle [0,5]}$ liegen („in der Wohnung ${\displaystyle [0,5]}$ leben“).

Die Kollektion der Bahnen ${\displaystyle [x]}$ definiert nun den Orbitraum („Menge der Wohnungen“) der Operation von ${\displaystyle G}$ auf ${\displaystyle X}$, bezeichnet als ${\displaystyle G\backslash X}$. Zum Beispiel ist

${\displaystyle \mathbb {Z} \backslash \mathbb {R} \cong [0,1)}$ (Schreibweise für halboffenes Intervall von 0 (abgeschlossen) bis 1 (offen); das Symbol ${\displaystyle \cong }$ bedeutet, es lassen sich beide Objekte identifizieren),

denn jede reelle Zahl ${\displaystyle x}$ besitzt genau ein eindeutig bestimmtes Element ${\displaystyle 0\leq y<1}$, das durch die Gruppenoperation mit ${\displaystyle \mathbb {Z} }$ aus ${\displaystyle x}$ hervorgeht. In etwa ist ${\displaystyle (10)(-9,8)=0,2\in [0,1)}$. Geometrisch lässt sich dies dadurch deuten, dass jede reelle Zahl auf dem Zahlenstrahl durch Translation um den Wert 1 nach links oder rechts irgendwann im Intervall ${\displaystyle [0,1)}$ landet – aber dies auf eindeutige Weise.

Zu beachten ist, dass ${\displaystyle [0,1)}$ lediglich eine (nützliche) Darstellung des Orbitraums ist – und damit keineswegs eindeutig. So wäre ${\displaystyle [1,2)}$ ebenfalls eine legitime Darstellung, wenn (ebenfalls immer eindeutig existierende) Klassenvertreter im Intervall ${\displaystyle 2\leq x<3}$ gewählt werden, aber zum Beispiel auch ${\displaystyle (\pi ,\pi +1]}$. In einigen Anwendungen ist es jedoch zweckmäßig, den Orbiträumen „kleine Mengen“ hinzuzufügen, um sie „mathematisch schöner“ zu machen. In etwa kann es von Vorteil sein, dass abgeschlossene Intervall ${\displaystyle [0,1]}$ als „Orbitraum“ zu betrachten, da es eine kompakte Menge in den reellen Zahlen ist. Dies ist für die Theorie der Modulformen ebenfalls wichtig: Auch hier ist es üblich, die Orbiträume geringfügig abzuändern, um sie später leichter behandeln zu können.^[7]

Im Falle der oberen Halbebene ${\displaystyle \mathbb {H} }$ und der vollen Modulgruppe ${\displaystyle \mathrm {SL} _{2}(\mathbb {Z} )}$ können ebenfalls Orbiträume ${\displaystyle \mathrm {SL} _{2}(\mathbb {Z} )\backslash \mathbb {H} }$ angegeben werden. Durch geringfügige Änderungen am Rand (wie oben beim Übergang von ${\displaystyle [0,1)}$ zu ${\displaystyle [0,1]}$) hat sich jedoch hier der Begriff des Fundamentalbereichs etabliert. Der sog. Standardfundametalbereich der Operation von ${\displaystyle \mathrm {SL} _{2}(\mathbb {Z} )}$ auf ${\displaystyle \mathbb {H} }$ hat die Gestalt^[8]

${\displaystyle {\mathcal {F}}=\left\{z\in \mathbb {H} \,\,\colon \,\,\left|z\right|\geq 1,\,\left|\,{\mbox{Re}}(z)\,\right|\leq {\tfrac {1}{2}}\right\}.}$

Dabei bedeutet:

• ${\displaystyle \left|z\right|\geq 1}$, dass ${\displaystyle z}$ außerhalb der komplexen Einheitskreisscheibe liegt,
• ${\displaystyle \left|\,{\mbox{Re}}(z)\,\right|\leq {\tfrac {1}{2}}}$, dass ${\displaystyle z}$ im Streifen zwischen Realteil ${\displaystyle -{\tfrac {1}{2}}}$ und ${\displaystyle {\tfrac {1}{2}}}$ liegt.

• 
  Der Standardfundamentalbereich ${\displaystyle {\mathcal {F}}}$ in grau schattiert. Manchmal wird dies auch als Modulfigur bezeichnet.^[8] Die obere Halbebene lässt sich durch Fundamentalbereiche der vollen Modulgruppe überdecken.
• 
  Die zwei parallelen Linien an der Modulfigur treffen sich mit der „richtigen Perspektive“ im unendlich fernen Punkt. Dieser wird auch noch beachtet, wenn es um die Definition von Modulformen geht. Modulformen dürfen nicht zu schnell wachsen, wenn die Funktionswerte diesem Punkt „näher kommen“.

Sehr kurz und einfach gesprochen motiviert sich der Begriff der automorphen Form aus zwei Ideen:

1. Man beginnt mit einer Funktion ${\displaystyle f}$ auf einem Definitionsbereich ${\displaystyle X}$, auf dem eine Gruppe ${\displaystyle G}$ operiert, mit Werten zum Beispiel in den komplexen Zahlen. Diese Funktion soll (in einem gewissen Sinne) unter der Gruppenwirkung unverändert, also invariant, sein. Dies gibt die Möglichkeit, sie zu einer Funktion auf dem Orbitraum ${\displaystyle G\backslash X}$ „einzuschränken“.
2. Es soll ${\displaystyle f}$ „gute analytische Eigenschaften“ haben, je nach Kontext (und Definitionsbereich) etwa Stetigkeit, Differenzierbarkeit, Glattheit oder sogar Holomorphie.

Dem oberen Beispiel folgend kann ${\displaystyle X=\mathbb {R} }$, ${\displaystyle G=\mathbb {Z} }$ und ${\displaystyle f(x)=\sin(2\pi x)}$ gewählt werden. Da der Sinus ${\displaystyle 2\pi }$-periodisch ist, gilt

${\displaystyle f(x+1)=f(x)}$ für alle ${\displaystyle x\in \mathbb {R} }$,

weshalb ${\displaystyle f}$ unter der Gruppenoperation von ${\displaystyle \mathbb {Z} }$ auf ${\displaystyle \mathbb {R} }$ invariant bleibt:

${\displaystyle \ldots =f(x-3)=f(x-2)=f(x-1)=f(x)=f(x+1)=f(x+2)=f(x+3)=\ldots .}$

Also reicht es aus, die Funktion ${\displaystyle f}$ auf dem Intervall ${\displaystyle [0,1)\cong \mathbb {Z} \backslash \mathbb {R} }$ (oder auch ${\displaystyle [0,1]}$) zu betrachten; wegen der Periodizität kennt man dann automatisch ihr gesamtes Abbildungsverhalten ${\displaystyle \mathbb {R} \to \mathbb {R} }$. Mathematisch ausgedrückt: ${\displaystyle f}$ induziert auf natürliche Weise eine Abbildung

${\displaystyle {\widetilde {f}}\colon \mathbb {Z} \backslash \mathbb {R} \longrightarrow \mathbb {R} }$, mit ${\displaystyle {\widetilde {f}}([x]):=f(x).}$

Es besitzt der Sinus aber auch „gute analytische Eigenschaften“: Er ist beliebig oft differenzierbar und kann sogar holomorph nach ${\displaystyle \mathbb {C} }$ fortgesetzt werden.

In der Mathematik zeigt sich, dass die Kombination aus einer „Form der Invarianz“ und „guten analytischen Eigenschaften“ immer wieder zu verblüffenden Ergebnissen führt. Das obere Beispiel aufgreifend gilt etwa:

Es ist also jedes solche ${\displaystyle f}$ aus Sinus- und Kosinus-Bausteinen „auf eindeutige Weise zusammengesetzt“, mit weitreichenden Konsequenzen in Analysis, Physik und Signalverarbeitung.

Elliptische Modulformen zur vollen Modulgruppe sind automorphe Formen hinsichtlich ${\displaystyle X=\mathbb {H} }$ und ${\displaystyle G=\mathrm {SL} _{2}(\mathbb {Z} )}$. Als „analytische Bedingung“ wird hierbei meist Meromorphie oder Holomorphie (= ganze Modulform) verlangt, es gibt aber zahlreiche Verallgemeinerungen, die auch schwächere Bedingungen zulassen. Fordert man nun eine Invarianz im strikten Sinne, so ist eine ganze Modulform eine holomorphe Funktion auf der oberen Halbebene, sodass

${\displaystyle f\left({\frac {az+b}{cz+d}}\right)=f(z)}$ für alle ganzen Zahlen ${\displaystyle a,b,c,d}$ mit ${\displaystyle ad-bc=1}$,

oder in Termen der Gruppenoperation

${\displaystyle f(M(z))=f(z)}$ für alle ${\displaystyle M\in \mathrm {SL} _{2}(\mathbb {Z} )}$,

wenn zusätzlich der Wert ${\displaystyle \lim _{\mathrm {Im} (z)\to \infty }f(z)}$ existiert. Konkrete Beispiele sind etwa

${\displaystyle f(z+1)=f(z),\qquad f\left(-{\frac {1}{z}}\right)=f(z)\qquad }$ aber auch ${\displaystyle \qquad f\left({\frac {5z-3}{-3z+2}}\right)=f(z).}$

Zu beachten ist,

1. dass diese Funktionalgleichungen – und unendlich viele weitere – alle gleichzeitig erfüllt sein müsssen, was dem Abbildungsverhalten von ${\displaystyle f}$ eine „starke Symmetrie“ verleiht, und
2. mit der geforderten Holomorphie (die u. a. Glattheit, Differenzierbarkeit und Stetigkeit impliziert) eine ganz besonders starke und damit restriktive analytische Bedingung gestellt wird.

In diesem Fall spricht man auch von einer (ganzen) Modulfunktion.

• 
  Die obere Halbebene, überdeckt von Fundamentalbereichen der Operation der ${\displaystyle \mathrm {SL} _{2}(\mathbb {Z} )}$. In etwa sendet die „Involution“ ${\displaystyle z\mapsto -{\tfrac {1}{z}}}$ den grau gefärbten Standardfunamentalbereich auf das „gebogene Dreieck“ direkt unter ihm.^[11]
• 
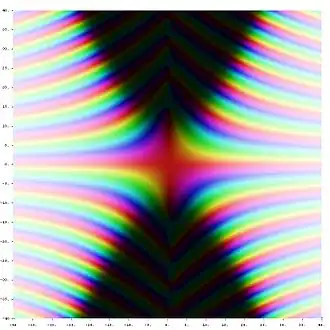
  Schaubild der j-Funktion, einer Modulfunktion. Sie ist überall holomorph, aber unbeschränkt für wachsende Imaginärteile. Ihre enorme Symmetrie zeigt sich dadurch, dass sie ich nur 1-periodisch, sondern zum Beispiel auch invariant unter der „Involutionssymmetrie“ ${\displaystyle z\mapsto -{\tfrac {1}{z}}}$ ist. Es lässt sich die Gestalt der Fundamentalbereiche (linkes Bild) erahnen: In jedem solchen taucht jede mögliche Färbung als Einzelpunkt genau einmal auf, da die j-Funktion dort 1:1 in die komplexen Zahlen abbildet.^[12] Die Farbspektren werden durch die jeweiligen „Schlieren“ vollständig abgedeckt.
• 
  Im Vergleich (selber Ausschnitt): Auch der komplexe Sinus ${\displaystyle \sin(2\pi z)}$ ist 1-periodisch, aber hat darüber hinaus nicht so viele Symmetrien.

In etwa ist die Kombination aus absoluter invarianz, Holomorphie in jedem Punkt, sowie Beschränktheit für wachsenden Imaginärteil derart restriktiv, dass gilt:

Es gibt also keine nichttrivialen ganzen Modulfunktionen. Daher zeigt sich in der Anwendung, dass entweder die Forderung absoluter Invarianz oder globaler Holomorphie in vielen Fällen zu restriktiv ist, weshalb man diese Abschwächt und damit zum Begriff der Modulform kommt.^[14] Diese Abschwächung vollzieht sich durch Einführung eines weiteren Parameters, der im klassischen Fall eine ganze Zahl ist. und meistens mit ${\displaystyle k}$ bezeichnet wird. Genannt wird dieser Parameter auch das Gewicht. Im einfachsten Falle spricht man bei einer holomorphen Funktion ${\displaystyle f\colon \mathbb {H} \to \mathbb {C} }$ von einer ganzen, elliptischen Modulform des Gewichts ${\displaystyle k\in \mathbb {Z} }$ zur vollen Modulgruppe, wenn zwei Bedingungen erfüllt sind:

1. Funktionalgleichungen: ${\displaystyle (cz+d)^{-k}f\left({\frac {az+b}{cz+d}}\right)=f(z)}$ für alle ganzen Zahlen ${\displaystyle a,b,c,d}$ mit ${\displaystyle ad-bc=1}$ und alle ${\displaystyle z\in \mathbb {H} }$,
2. Wachstumsbedingung: ${\displaystyle \lim _{\mathrm {Im} (z)\to \infty }f(z)}$ existiert (mit dem Imaginärteil ${\displaystyle \mathrm {Im} (z)}$).

Der Fall ${\displaystyle k=0}$ entspricht dann dem der ganzen Modulfunktion, da stets ${\displaystyle (cz+d)^{0}=1}$. Jedoch tauchen im ganzen Falle hier nur konstante Funktionen auf. Durch die Wahl ${\displaystyle a=b=d=1}$ und ${\displaystyle c=0}$ ergibt sich ferner

${\displaystyle f(z+1)=f(z)}$,

weshalb jede Modulform eine 1-periodische Funktion ist.

Modulformen sind keine Funktionen mehr, zumindest nicht auf ${\displaystyle \mathrm {SL} _{2}(\mathbb {Z} )\backslash \mathbb {H} }$, da der Faktor ${\displaystyle (cz+d)^{-k}}$ für ${\displaystyle k\not =0}$ im Allgemeinen nicht 1 ist und somit keine absolute Invarianz mehr vorliegt. Dennoch ist ihre Definition aus mathematischer Sicht sehr nützlich, da sich der Begriff der Funktion ausweiten lässt. Zudem ist der Quotient ${\displaystyle {\tfrac {f}{g}}}$ zweier Modulformen (${\displaystyle g}$ nicht konstant 0) stets eine Modulfunktion, wenn auch nicht unbedingt eine ganze. Dies erlaubt gewissermaßen eine „Rückführung“ der Theorie der Modulformen auf jene der Modulfunktionen.

Ein Grundprinzip der Zahlentheorie ist, dass die natürlichen Zahlen sich multiplikativ aus den Primzahlen zusammensetzen. Jede Zahl lässt sich eindeutig als Produkt von Primzahlen schreiben, etwa

${\displaystyle 12=2\cdot 2\cdot 3=2^{2}\cdot 3}$ mit den Primzahlen ${\displaystyle 2}$ und ${\displaystyle 3}$.

Diese Zerlegung bildet das Fundament fast aller arithmetischen Überlegungen, weshalb der diesbezügliche Satz auch als Fundamentalsatz der Arithmetik bezeichnet wird.

In der Zahlentheorie untersucht man oft Folgen ganzer Zahlen, die zu jeder natürlichen Zahl einen Wert zuordnen. Ein erstes Beispiel ist die Folge der Quadratzahlen:

${\displaystyle 1,\;\;4,\;\;9,\;\;16,\;\;25,\;\;36,\;\;49,\;\;64,\;\;81,\;\;100,\;\;121,\;\;\ldots }$ usw.

Die Schwierigkeit solcher Untersuchungen hängt sehr stark von der Art der Zahlenfolge, aber auch der Fragestellung ab. Manchmal reicht es für Anwedungen, etwa aus der Komplexitätstheorie, bereits aus, abzuschätzen, wie schnell eine Folge anwächst (polynomiell, exponentiell,…?). In der reinen Mathematik ist man darüber hinaus auch an der „Struktur der Zahlen selbst“ interessiert, weshalb man mitunter nach stärkeren Resultaten sucht, etwa nach exakten Formeln, mit denen man jedes beliebige Folgeglied schnell berechnen kann, oder „Wahrscheinlichkeiten“, dass eine „zufällig gewählte“ Zahl eine bestimmte Eigenschaft erfüllt (in einem asymptotischen Sinne).

Zahlenfolgen werden häufig durch ${\displaystyle a_{n}}$ (bei mehreren Folgen ${\displaystyle b_{n},c_{n}}$ usw.) ausgedrückt. Im Falle der Quadratzahlen hat man dann

${\displaystyle a_{1}=1,\;\;a_{2}=4,\;\;a_{3}=9\;\;}$ usw.

Manche dieser Folgen sind vollständig multiplikativ: Es gilt in diesem Falle für natürliche ${\displaystyle m,n}$^[15]

${\displaystyle a_{mn}=a_{m}\,a_{n},}$ und ${\displaystyle a_{1}=1.}$

Das Produkt der Werte ist also gleich dem Wert am Produkt. Etwa die Quadratzahlen erfüllen diese Eigenschaft. Sehen lässt sich dies anhand des Kommutativgesetzes:

${\displaystyle m^{2}\cdot n^{2}=m\cdot m\cdot n\cdot n=m\cdot n\cdot m\cdot n=(m\cdot n)^{2},}$ zum Beispiel gilt ${\displaystyle 2^{2}\cdot 5^{2}=4\cdot 25=100=10^{2}=(2\cdot 5)^{2}.}$

Folgerung: Es genügt, die Quadratzahlen aller Primzahlen zu kennen,

${\displaystyle {\color {red}{4}},\;\;9,\;\;{\color {red}{25}},\;\;49,\;\;121,\;\;}$ usw.

denn die restlichen Quadratzahlen setzen sich multiplikativ aus diesen zusammen. Etwa ist ${\displaystyle 100}$ nicht in oberer Liste, aber es gilt ${\displaystyle {\color {red}{4}}\cdot {\color {red}{25}}=100}$. Hat man also ganz allgemein eine Primfaktorzerlegung

${\displaystyle n=p_{1}^{t_{1}}\,p_{2}^{t_{2}}\cdots p_{s}^{t_{s}},}$

so folgt im vollständig multiplikativen Falle die Berechnungsformel

${\displaystyle a_{n}=a_{p_{1}}^{t_{1}}\,a_{p_{2}}^{t_{2}}\cdots a_{p_{s}}^{t_{s}}}$ (oder anders ausgedrückt: ${\displaystyle a_{n}}$ ist durch die Werte ${\displaystyle a_{p}}$ bereits vollständig bestimmt).^[15]

In einigen Fällen ist dies jedoch zu restriktiv. Einige für die Zahlentheorie bedeutende Folgen sind nicht vollständig multiplikativ, erfüllen aber immer noch eine etwas schwächere Bedingung. Man nennt eine Folge ${\displaystyle a_{n}}$ multiplikativ, wenn für zwei teilerfremde Zahlen ${\displaystyle m}$ und ${\displaystyle n}$ stets^[16]

${\displaystyle a_{mn}=a_{m}\,a_{n}}$

gilt und ${\displaystyle a_{1}=1.}$ Es gilt die Berechnungsformel

${\displaystyle a_{n}=a_{p_{1}^{t_{1}}}a_{p_{2}^{t_{2}}}\cdots a_{p_{s}^{t_{s}}}.}$ (oder anders ausgedrückt: ${\displaystyle a_{n}}$ ist durch die Werte ${\displaystyle a_{p^{t}}}$ an Primzahlpotenzen bereits vollständig bestimmt).^[17]

Ein erstes, nichttriviales Beispiel ist die Teilersummenfunktion ${\displaystyle \sigma _{1}(n)}$, die alle positiven Teiler von ${\displaystyle n}$ addiert (aus Konventionsgründen steht das ${\displaystyle n}$ im Gegensatz zum „allgemeinen“ ${\displaystyle a_{n}}$ hier nicht im Index). Für ${\displaystyle m=3}$ ergibt sich

${\displaystyle \sigma _{1}(3)=1+3=4.}$

Für ${\displaystyle n=4}$ hat man

${\displaystyle \sigma _{1}(4)=1+2+4=7.}$

Multipliziert man, so erhält man

${\displaystyle \sigma _{1}(3)\cdot \sigma _{1}(4)=4\cdot 7=28.}$

Nun betrachtet man das Produkt ${\displaystyle mn=12}$. Die positiven Teiler von ${\displaystyle 12}$ sind ${\displaystyle 1,2,3,4,6,12}$ und ihre Summe ist

${\displaystyle \sigma _{1}(12)=1+2+3+4+6+12=28.}$

Also stimmt tatsächlich ${\displaystyle \sigma _{1}(3)\,\sigma _{1}(4)=\sigma _{1}(12)}$. Hier zeigt sich direkt das multiplikative Prinzip. Über elementare Zahlentheorie kann man für beliebige teilerfremde ${\displaystyle m,n}$^[18]

${\displaystyle \sigma _{1}(m)\,\sigma _{1}(n)=\sigma _{1}(mn)}$

beweisen; es werden nicht alle Werte „durchprobiert“ (was bei unendlich vielen Zahlen unmöglich ist), sondern es wird allgemein argumentiert. Jedoch ist ${\displaystyle \sigma _{1}}$ nicht vollständig multiplikativ, wie das Gegenbeispiel

${\displaystyle 7=\sigma _{1}(4)\not =\sigma _{1}(2)\,\sigma _{1}(2)=(1+2)\,(1+2)=9}$

sofort zeigt. Beachte, dass ${\displaystyle 4}$ und ${\displaystyle 2}$ nicht teilerfremd sind.

Sowohl die Folge der Quadratzahlen als auch die der Teilerfunktionen ${\displaystyle \sigma _{k}(n)}$ (bedeutet: alle ${\displaystyle k}$-ten Potenzen der positiven Teiler von ${\displaystyle n}$ werden addiert) spielen in der Theorie der Modulformen eine zentrale Rolle. Sie sind damit auf gewisse Weise „Nutznießer der modularen Symmetrie“.

Bei der Untersuchung beliebiger Zahlenfolgen ${\displaystyle a_{n}}$ stößt man schnell auf ein natürliches Hindernis: Die Unendlichkeit der natürlichen Zahlen. Es ist also schlicht nicht möglich, die tieferen Eigenschaften der Folge ${\displaystyle a_{n}}$ durch bloße „Berechnung“ oder „Auflistung aller Werte“ zu erfassen, da kein Supercomputer dazu imstande wäre – nicht mal, wenn alle Materie im sichtbaren Universum in reine Energie umgewandelt würde. Ein Hauptbestreben bei der Entwicklung der mathematischen Disziplin der Analysis war es, die Unendlichkeit „beherrschbar“ zu machen. In manchen Fällen kann ${\displaystyle a_{n}}$ schon mit elementaren Techniken, wie der vollständigen Induktion, untersucht werden (wobei die Unendlichkeit mit einem cleveren logischen Verfahren „umgangen“ wird). Bei dafür zu komplizierten Folgen kann es wiederum helfen, die zu ${\displaystyle a_{n}}$ gehörige erzeugende Funktion zu bilden. Dies ist eine „Datenreduktion“ in dem Sinne:

${\displaystyle {\text{''Unendlich'' viele Zahlen}}\;a_{n}\;\;\longrightarrow \;\;{\text{''eine'' Funktion}}\;f(x).}$

Mit anderen Worten: Es werden die unendlich vielen Werte ${\displaystyle a_{n}}$ in einer Funktion ${\displaystyle f(x)}$ „kodiert“. Im Anschluss ist die Strategie, die Funktion ${\displaystyle f(x)}$ zu analysieren, in der Hoffnung, das „Reduktionsverfahren umkehren zu können“:

${\displaystyle {\text{Informationen über}}\;f(x)\;\;{\overset {?}{\longrightarrow }}\;\;{\text{Informationen über die}}\;a_{n}.}$

Die erzeugende Funktion der Folge ${\displaystyle a_{n}}$ ist (im Regelfall^[19]) gegeben durch ihre Potenzreihe:

${\displaystyle f(x)=\sum _{n=1}^{\infty }a_{n}x^{n}=a_{1}x+a_{2}x^{2}+a_{3}x^{3}+a_{4}x^{4}+\cdots .}$

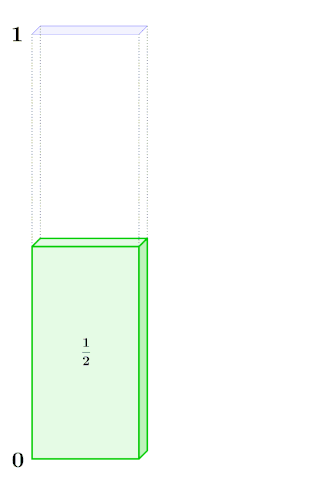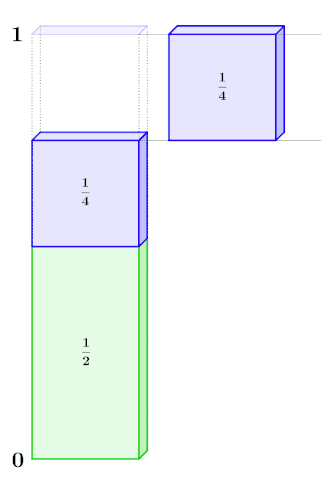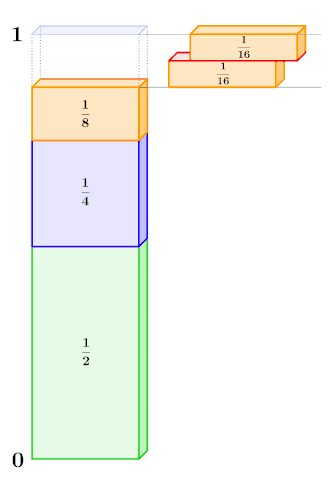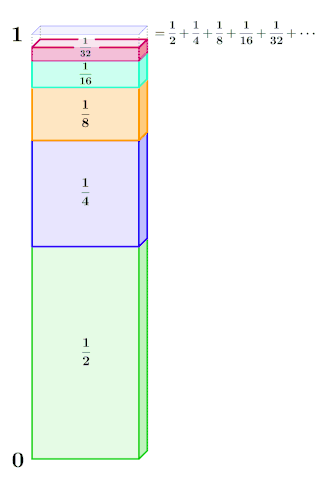
Je nach Kontext beginnt ${\displaystyle f(x)}$ bereits bei ${\displaystyle a_{0}x^{0}=a_{0}}$. Ein – auch im Kontext der Modulformen – wichtiges, nichttriviales Beispiel ist die erzeugende Funktion der Partitionsfunktion ${\displaystyle p(n)}$. Diese zählt, wie oft sich eine natürliche Zahl als Summe nicht aufsteigender natürlicher Zahlen schreiben lässt.^[20] Etwa ist ${\displaystyle p(4)=5}$, denn

${\displaystyle {\begin{aligned}4&=4\\&=3+1\\&=2+2\\&=2+1+1\\&=1+1+1+1.\end{aligned}}}$

Eine einfache, geschlossene Form für ${\displaystyle p(n)}$ – das mit ${\displaystyle n\to \infty }$ schnell anwächst – zu finden, ist keine einfache Aufgabe. Allerdings ist mit elementaren Mitteln möglich, eine „geschlossene Gestalt“ der erzeugenden Funktion mittels eines unendlichen Produktes anzugeben:^[21]

${\displaystyle \sum _{n=0}^{\infty }p(n)x^{n}=1+x+2x^{2}+3x^{3}+5x^{4}+\cdots ={\frac {1}{(1-x)(1-x^{2})(1-x^{3})\cdots }}=\prod _{n=1}^{\infty }{\frac {1}{1-x^{n}}}.}$ (Man setzt ${\displaystyle p(0):=1}$.)

Reihe und Produkt konvergieren dabei im Falle ${\displaystyle |x|<1}$, da hier die Summenterme ${\displaystyle p(n)x^{n}}$ für wachsende ${\displaystyle n}$ exponentiell kleiner werden, und das Wachstum der erzeugenden Funktion für ${\displaystyle x\to 1}$ (von unten) gibt Aufschluss über das Wachstum von ${\displaystyle p(n)}$, siehe unten.

Mit der erzeugenden Funktion überträgt sich das Unendlichkeitsproblem auf ein analytisches Konvergenzproblem; wachsen die ${\displaystyle a_{n}}$ jedoch nicht zu stark an, wird die Reihe ${\displaystyle \textstyle \sum _{n=1}^{\infty }a_{n}x^{n}}$ für gewisse Werte ${\displaystyle x\not =0}$ konvergieren und dort eine analytische Funktion (für komplexe ${\displaystyle x}$ sogar holomorphe Funktion) darstellen. Dies ist eine starke Struktur und ist bei der Untersuchung von ${\displaystyle f(x)}$ von Nutzen. Man fragt etwa nach dem Wachstum, nach Mittelwerten oder nach Beziehungen von ${\displaystyle f(x)}$ zu anderen Funktionen. So lassen sich aus den scheinbar einfachen Definitionen tiefe Informationen über die Zahlenfolgen und letztlich über die Struktur der natürlichen Zahlen „entschlüsseln“. Beispiele für Techniken in diesem Kontext sind der Identitätssatz für Potenzreihen, Partialbruchzerlegung und Rückführung auf geometrische Reihen (wenn ${\displaystyle f(x)}$ eine rationale Funktion ist, wie etwa im Falle der Fibonacci-Folge^[22]), noch allgemeiner die Methode subtrahierter Singularitäten,^[23] die Kreismethode,^[24] aber auch Taubersätze.^[25]

Modulformen sind – in ihrer einfachsten Form – nichts anderes als erzeugende Funktionen zu ganz bestimmten Zahlenfolgen. Dabei wird allerdings in der Literatur nicht die Variable ${\displaystyle x}$, sondern traditionell ${\displaystyle q}$ verwendet. Hintergrund ist, dass die eigentliche Variable einer Modulform nicht ${\displaystyle q}$ ist, sondern ${\displaystyle z}$ mit^[26]

${\displaystyle q:=e^{2\pi iz}.}$

Die erzeugende Reihe ist also eine Potenzreihe in ${\displaystyle q}$, und eine komplexe Fourier-Reihe in ${\displaystyle z}$:

${\displaystyle \sum _{n=0}^{\infty }a_{n}q^{n}=\sum _{n=0}^{\infty }a_{n}e^{2\pi izn}.}$ (Hinweis: Dieser Variablenwechsel ist für jede Potenzreihe möglich, nicht nur Modulformen.)

Hierbei ist ${\displaystyle e^{x}}$ die natürliche Exponentialfunktion, fortgesetzt auf die komplexen Zahlen. Es gilt mit der Eulerschen Formel mit ${\displaystyle z=x+iy}$ die Berechnungsformel

${\displaystyle e^{2\pi izn}=e^{2\pi i(x+iy)n}=e^{-2\pi yn}e^{2\pi ixn}=e^{-2\pi yn}(\cos(2\pi xn)+i\sin(2\pi xn)).}$

Wegen dieser „Zerlegung“ in Sinus und Kosinus spricht man von Fourier-Reihe. Die Reihenterme ${\displaystyle a_{n}e^{2\pi izn}}$ sind ergo alle 1-periodisch in ${\displaystyle x}$, also sogar unverändert unter ${\displaystyle z\mapsto z+1}$, da 1 eine reelle Zahl ist, also „zu ${\displaystyle x}$ zählt“. Für Werte ${\displaystyle y>0}$ (also ${\displaystyle z}$ auf der oberen Halbebene!) sind die Werte ${\displaystyle e^{2\pi izn}}$ außerdem „zunehmend klein“, da dann ${\displaystyle e^{-2\pi yn}}$ für wachsendes ${\displaystyle n\to \infty }$ exponentiell gegen 0 strebt. Also hat die Reihe auf der oberen Halbebene gute Konvergenzbedingungen, etwa wenn die Zahlen ${\displaystyle a_{n}}$ nur polynomiell wachsen (was bei Modulformen im einfachsten Falle der Fall ist).

• 
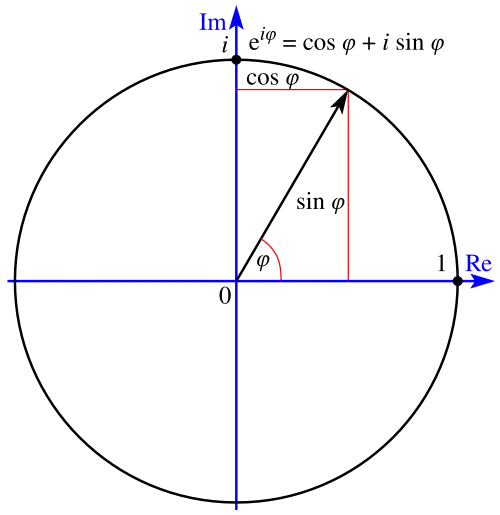  Illustration der Eulerschen Formel. Der Zusammenhang zwischen Trigonometrie und der Exponentialfunktion hat starke Auswirkungen für die gesamte Mathematik – nicht nur die Theorie der Modulformen.
• 
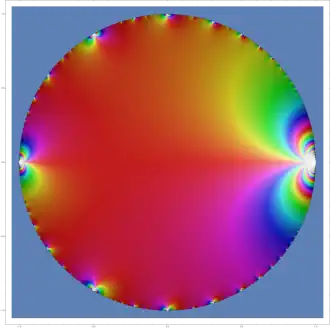
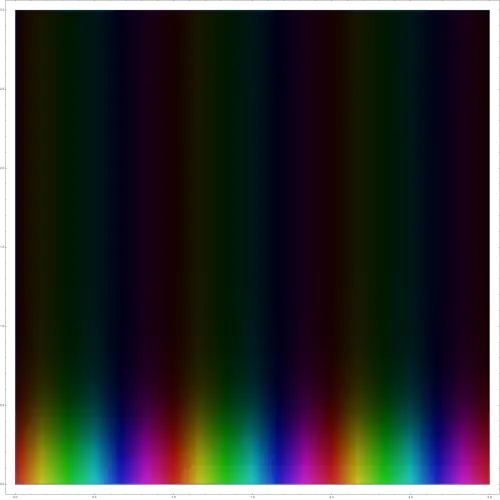  Auf der oberen Halbebene wird die Funktion ${\displaystyle e^{2\pi iz}}$ für steigende Imaginärteile (vertikale Achse) im Betrag schnell klein, wie man an der zunehmend dunklen Schattierung sieht (schwarz = 0). Entlang der (horizontalen) reellen Achse ist sie wegen der Eulerschen Formel 1-periodisch. Aus diesem Grund haben Reihen der Form ${\displaystyle \textstyle \sum _{n=0}^{\infty }a_{n}e^{2\pi izn}}$ hier „gute Konvergenzbedingungen“. Ist etwa ${\displaystyle a_{n}}$ subexponentiell ansteigend, gilt stets ${\displaystyle a_{n}e^{2\pi izn}{\overset {n\to \infty }{\longrightarrow }}0}$ (${\displaystyle z\in \mathbb {H} )}$ mit exponentieller Geschwindigkeit, und die Reihe konvergiert gegen eine 1-periodische Funktion.
• 
  Veranschaulichung des Variablenwechsels ${\displaystyle q=e^{2\pi iz}}$. Die Graphik selbst zeigt allerdings nur den vereinfachten Fall ${\displaystyle q=e^{z}}$; es muss noch mit ${\displaystyle 2\pi i}$ „nachskaliert“ werden.

Potenz- bzw. Fourier-Reihen sind klassische Werkzeuge in der additiven Zahlentheorie. Hintergrund ist das Potenzgesetz

${\displaystyle q^{m}q^{n}=q^{n+m}}$ (heißt: ${\displaystyle m}$ Faktoren mal ${\displaystyle n}$ Faktoren ${\displaystyle q}$ ergibt insgesamt ${\displaystyle m+n}$ Faktoren ${\displaystyle q}$.)

Ein klassisches Beispiel liefert die sog. Jacobische Thetafunktion (eine Modulform! - siehe unten in diesem Artikel)^[28]

${\displaystyle \theta (z):=1+2q+2q^{4}+2q^{9}+2q^{16}+\cdots \;=\;\sum _{n=-\infty }^{\infty }q^{n^{2}}.}$

Hier tritt in der Potenzreihe zu jeder Quadratzahl ${\displaystyle n^{2}}$ ein Koeffizient auf: nämlich ${\displaystyle 1}$ für ${\displaystyle n=0}$ und ${\displaystyle 2}$ für jedes positive ${\displaystyle n}$, da sowohl ${\displaystyle +n}$ als auch ${\displaystyle -n}$ denselben Exponenten ergeben.

Der eigentliche Bezug zur additiven Zahlentheorie entsteht, wenn man ${\displaystyle \theta (z)}$ zum Beispiel quadriert, und beim Ausmultiplizieren der Klammern das obere Potenzgesetz ausnutzt:

${\displaystyle \theta (z)^{2}\;=\;\left(1+2q+2q^{4}+2q^{9}+2q^{16}+\cdots \right)^{2}=1+4q+4q^{2}+4q^{4}+8q^{5}+4q^{8}+4q^{9}+\cdots .}$

Die neu entstandenen Koeffizienten lassen sich wie folgt Interpretieren: Sie zählen bei der Potenz ${\displaystyle q^{N}}$ genau, wie viele ganzzahlige Darstellungen ${\displaystyle N=m^{2}+n^{2}}$ existieren, unter Beachtung der Reihenfolge.^[29] In etwa gilt

${\displaystyle 3^{2}+0^{2}=(-3)^{2}+0^{2}=0^{2}+3^{2}=0^{2}+(-3)^{2}=9}$

weshalb es hier 4 Möglichkeiten gibt, daher ${\displaystyle 4q^{9}}$. Bezeichet werden diese auch als ${\displaystyle r_{2}(n)}$, also hat man

${\displaystyle \theta (z)^{2}=\sum _{n=0}^{\infty }r_{2}(n)q^{n}.}$

Da Produkte von Modulformen wieder Modulformen sind (siehe unten), gilt

${\displaystyle \theta (z)\;\;{\text{Modulform}}\;\;\implies \;\theta (z)^{2}\;\;{\text{Modulform}}.}$

Somit lässt sich etwa die nichttriviale Zahlenfolge ${\displaystyle r_{2}(n)}$ mit Hilfe der Theorie der Modulformen untersuchen. Allerdings ist man wegen der Redundanzen durch Vorzeichen an der „bereinigten“ Funktion ${\displaystyle r_{2}^{*}(n):={\tfrac {1}{4}}r_{2}(n)}$ mehr interessiert, also

${\displaystyle {\frac {1}{4}}\theta (z)^{2}=\sum _{n=0}^{\infty }r_{2}^{*}(n)q^{n}={\frac {1}{4}}+q+q^{2}+q^{4}+2q^{5}+q^{8}+q^{9}+\cdots .}$ (Wegen ${\displaystyle \pm 0=0}$ wird die Null nur „halb gewichtet“, es sind damit zum Beispiel ${\displaystyle 1^{2}+2^{2}}$ und ${\displaystyle 2^{2}+1^{2}}$ und ${\displaystyle 3^{2}+0^{2}}$ die „im Wesentlichen“ eindeutigen Darstellungen von 5 bzw. 9; daher ${\displaystyle 2q^{5}}$ und ${\displaystyle q^{9}}$.)

Es wird ignoriert, dass der „triviale Fall“ Null einen Bruch liefert.

Das, was Modulformen unter anderem so wichtig für die Zahlentheorie macht, ist, dass sie neben der additiven auch eine enge Beziehung zur multiplikativen Zahlentheorie haben. Während in der additiven Zahlentheorie „Fragen über Summen ganzer Zahlen“ nachgegangen wird, geht es bei der Multiplikativen um Produkte. Etwa sind die multiplikativen Zahlenfolgen ihr Gegenstand – ebenso wie die Primzahlen.

Als Beispiel wird wieder

${\displaystyle {\begin{aligned}{\frac {1}{4}}\theta (z)^{2}=&{\frac {1}{4}}+q+q^{2}+q^{4}+2q^{5}+q^{8}+q^{9}+2q^{10}+2q^{13}+q^{16}+2q^{17}+q^{18}+2q^{20}\\&+3q^{25}+2q^{26}+2q^{29}+q^{32}+2q^{34}+q^{36}+2q^{37}+2q^{40}+2q^{41}+2q^{45}+\cdots \end{aligned}}}$

herangezogen. Es lässt sich zum Beispiel direkt ablesen:

${\displaystyle r_{2}^{*}(3)r_{2}^{*}(8)=0\cdot 1=r_{2}^{*}(24),\qquad r_{2}^{*}(2)r_{2}^{*}(5)=1\cdot 2=r_{2}^{*}(10),\qquad r_{2}^{*}(5)r_{2}^{*}(8)=2\cdot 1=r_{2}^{*}(40).}$

Diese Beispiele lassen vermuten, dass ${\displaystyle r_{2}^{*}(n)}$ eine multiplikative Zahlenfolge ist. Dies ist tatsächlich der Fall; allgemein gilt für teilerfremde natürliche Zahlen ${\displaystyle m,n}$

${\displaystyle r_{2}^{*}(m)r_{2}^{*}(n)=r_{2}^{*}(mn).}$

Dies zu sehen, ist nicht ganz einfach; dennoch kann es mit elementaren Methoden bewiesen werden. Betrachtet man aber nun

${\displaystyle {\frac {1}{2}}\theta (z)={\frac {1}{2}}+q+q^{4}+q^{9}+q^{16}+q^{25}+q^{36}+q^{49}+q^{64}+q^{81}+\cdots }$

so fällt auf, dass auch hier eine multiplikative Zahlenfolge zugrunde liegt (es wird ${\displaystyle {\tfrac {1}{2}}}$ ignoriert). Die Koeffizienten sind hier die Indikatorfunktion ${\displaystyle I_{\square }(n)}$ der Quadratzahlen, also sie „zeigt 1“, wenn eine Quadratzahl vorliegt, und ansonsten „zeigt sie 0“. Nun ist aber das Produkt zweier teilerfremder Zahlen genau dann eine Quadratzahl, wenn beide Faktoren schon eine waren (dies sieht man an der Primfaktorzerlegung; Primzahlen müssen bei Quadraten immer in gerader Häufigkeit auftreten). Zum Beispiel:

${\displaystyle \underbrace {I_{\square }\left(\underbrace {100} _{={\text{Quadratzahl}}}\right)} _{=1}=\underbrace {I_{\square }\left(\underbrace {4} _{={\text{Quadratzahl}}}\right)} _{=1}\;\;\underbrace {I_{\square }\left(\underbrace {25} _{={\text{Quadratzahl}}}\right)} _{=1}=1,}$ und es sind ${\displaystyle 4,25}$ teilerfremd.

Zusammenfassend wurde ${\displaystyle r_{2}^{*}(n)}$ also auf „additivem Wege“ (im Sinne von Ausmultiplizieren und Nutzen von ${\displaystyle q^{m}q^{n}=q^{m+n}}$) über eine multiplikative Zahlenfolge gewonnen, aber das Ergebnis ist wieder multiplikativ. Dies ist aus mathematischer Sicht äußerst ungewöhnlich, und kann mit Hilfe der Theorie der Modulformen erklärt werden.

Neben den erzeugenden Funktionen in Form von Potezreihen kann man Zahlenfolgen ${\displaystyle a_{n}}$ auch andere Reihen zuordnen. Wegen des Potenzgesetzes

${\displaystyle m^{x}n^{x}=(mn)^{x}}$ (heißt: ${\displaystyle x}$ Faktoren ${\displaystyle m}$ mal ${\displaystyle x}$ Faktoren ${\displaystyle n}$ ergeben ${\displaystyle x}$ Faktoren ${\displaystyle mn}$)

ist für die multiplikative Zahlentheorie die Zuordnung

${\displaystyle L(s)=\sum _{n=1}^{\infty }{\frac {a_{n}}{n^{s}}}=a_{1}+{\frac {a_{2}}{2^{s}}}+{\frac {a_{3}}{3^{s}}}+{\frac {a_{4}}{4^{s}}}+{\frac {a_{5}}{5^{s}}}+\cdots }$

sinnvoll. Dieser Typ Reihe heißt Dirichlet-Reihe. Bedeutend ist in diesem Kontext das Euler-Produkt. Dirichlet-Reihen drücken die oben diskutierte Tatsache, dass multiplikative Funktionen durch ihre Werte an Primzahlpotenzen eindeutig bestimmt sind, analytisch aus. Ist also ${\displaystyle a_{n}}$ multiplikativ, gilt^[30]

${\displaystyle {\begin{aligned}\sum _{n=1}^{\infty }{\frac {a_{n}}{n^{s}}}&=a_{1}+{\frac {a_{2}}{2^{s}}}+{\frac {a_{3}}{3^{s}}}+\cdots \\&=\prod _{p\,{\text{Primzahl}}}\left(1+{\frac {a_{p}}{p^{s}}}+{\frac {a_{p^{2}}}{p^{2s}}}+\cdots \right)\\&=\left(1+{\frac {a_{2}}{2^{s}}}+{\frac {a_{4}}{4^{s}}}+\cdots \right)\left(1+{\frac {a_{3}}{3^{s}}}+{\frac {a_{9}}{9^{s}}}+\cdots \right)\left(1+{\frac {a_{5}}{5^{s}}}+{\frac {a_{25}}{25^{s}}}+\cdots \right)\cdots .\end{aligned}}}$

In der Tat nutzt die rechte Seite nur noch ${\displaystyle a_{p^{t}}}$ zur Berechnung – und der Beweis nutzt termweises Ausmultiplizieren der Klammern, mit anschließendem Zusammenfassen mit Hilfe der Regel ${\displaystyle a_{n}=a_{p_{1}^{t_{1}}}a_{p_{2}^{t_{2}}}\cdots a_{p_{s}^{t_{s}}}}$, wenn ${\displaystyle n=p_{1}^{t_{1}}\cdots p_{s}^{t_{s}}}$.

Bei Modulformen nennt man die Dirichlet-erzeugende Funktion schlicht L-Reihe. Also hat man eine Zuordnung

${\displaystyle \{{\text{Modulformen}}\}\;\;\longrightarrow \;\{{\text{L-Reihen}}\}}$

${\displaystyle \;\;\;\;\;\;\;\;\;\;\sum _{n=0}^{\infty }a_{n}q^{n}\;\;\,\,\longrightarrow \;\sum _{n=1}^{\infty }{\frac {a_{n}}{n^{s}}}.}$

Bei dieser Zuordnung wird ${\displaystyle a_{0}}$ auf der rechten Seite vorerst „ignoriert“, da die Null keine guten Eigenschaften in der multiplikativen Zahlentheorie hat – alles mal Null ist wieder Null.

Bedeutsam ist diese Zuordnung aus zwei zentralen Gründen:

1. Modulformen sind „extrem symmetrisch“, aber durch die Daten ${\displaystyle a_{n}}$ vollständig bestimmt. Es ist zu erwarten, dass sich diese Symmetrie auf die L-Reihe „überträgt“, da sie sich auch durch die ${\displaystyle a_{n}}$ definiert.
2. Ist die Zahlenfolge ${\displaystyle a_{n}}$ zusätzlich multiplikativ, so hat die L-Reihe ein Euler-Produkt. Im Falle eines solchen „Upgrades“ spricht man von einer L-Funktion (siehe auch Selberg-Klasse).

Hat eine Modulform also multiplikative Koeffizienten, erhält man in Kombination eine „symmetrische Funktion“ ${\displaystyle L(s)}$, die gleichzeitig „etwas über Primzahlen aussagt“. Dies ist der Schlüssel für die moderne Zahlentheorie.

Die Verstrickung additiver und multiplikativer Elemente der Zahlentheorie ist in der Theorie der Modulformen kein Zufall und findet ihre tiefere Erklärung in der sog. Hecke-Theorie, siehe unten.

Erster Prototyp eines Beispiels ist die Korrespondenz der Thetafunktion zur Riemannschen Zetafunktion

${\displaystyle \zeta (s)=\sum _{n=1}^{\infty }{\frac {1}{n^{s}}}=1+{\frac {1}{2^{s}}}+{\frac {1}{3^{s}}}+\cdots .}$

Hier erhält man (es wird ${\displaystyle a_{0}={\tfrac {1}{2}}}$ ignoriert)

${\displaystyle {\frac {1}{2}}\theta (z)={\frac {1}{2}}+q+q^{4}+q^{9}+q^{16}+\cdots \longrightarrow 1+{\frac {1}{4^{s}}}+{\frac {1}{9^{s}}}+{\frac {1}{16^{s}}}+\cdots =1+{\frac {1}{2^{2s}}}+{\frac {1}{3^{2s}}}+{\frac {1}{4^{2s}}}+\cdots =\zeta (2s).}$

Alle relevanten Koeffizienten sind 0 oder 1. Bei der letzten Umformung wurde das Potenzgesetz ${\displaystyle (n^{2})^{s}=n^{2s}}$ genutzt, um die Funktionsreihe der Zetafunktion besser „sichtbar“ zu machen; es sind insbesondere genau die Quadratzahlen in der Thetareihe, die zudem den Skalar ${\displaystyle 2}$ im Funktionsargument ${\displaystyle 2s}$ verantworten. Die Dirichlet-Reihe wird für Werte ${\displaystyle s}$ mit zu kleinem Realteil nicht konvergieren, etwa macht

„${\displaystyle \zeta (0)=1+1+1+1+1+\cdots }$“ (beachte: ${\displaystyle n^{0}=1}$)

keinen Sinn; mit Hilfe analytischer Fortsetzung kann die Zetafunktion ${\displaystyle \zeta (s)}$ aber auch in alle Bereiche (außer ${\displaystyle s=1}$) holomorph ausgedehnt werden, in der die Reihe nicht mehr konvergiert. Die Theorie holomorpher Funktionen garantiert, dass eine solche Fortsetzung eindeutig bestimmt ist, also gibt es trotz nur lokaler Konvergenz der Reihe nur „die eine“ Zetafunktion.

Das klassische Euler-Produkt der Zetafunktion besagt nun^[31]

${\displaystyle \zeta (2s)=\prod _{p\,\mathrm {Primzahl} }{\frac {1}{1-{\frac {1}{p^{2s}}}}}={\frac {1}{\left(1-{\frac {1}{2^{2s}}}\right)\left(1-{\frac {1}{3^{2s}}}\right)\left(1-{\frac {1}{5^{2s}}}\right)\cdots }}\;\;}$ (im Konvergenzbereich der Reihe).

Wie viele andere Funktionen kann die Zetafunktion aber auch durch ein Produkt über ihre Nullstellen konstruiert werden. Vergleichbar ist dies mit dem Polynom ${\displaystyle P(w)=w^{2}-1}$. Es hat Nullstellen bei ${\displaystyle w=\pm 1}$, aber es gilt ${\displaystyle P(w)=(w-1)(w+1)}$; ein Produkt aufgebaut aus Nullstellen. Die Aufstellung dieses Nullstellenproduktes für die analytisch kompliziertere Zetafunktion ist eine deutlich schwierigere Aufgabe als der Beweis des Euler-Produktes, da unter anderem das Problem unendlich vieler Nullstellen gelöst werden muss – dies gelang rigoros erst Ende des 19. Jahrhunderts durch Jacques Hadamard. Man erhält also eine „Identität zwischen Produkten, die dieselbe Funktion ergeben“:

${\displaystyle \zeta (s)=\prod _{\text{Primzahlen}}=\prod _{{\text{Nullstellen von}}\;\zeta (s)}.}$

Aus dieser erwächst eine Dualität^[32] zwischen Primzahlen und Nullstellen, und eine Folgerung ist, dass die Lage der Nullstellen die Verteilung der Primzahlen bestimmt.^[33] Nun ist die Thetafunktion jedoch eine Modulform, und durch ihre Funktionalgleichung^[28]

${\displaystyle \theta \left(-{\frac {1}{4z}}\right)={\sqrt {-2iz}}\;\theta (z)\qquad (z\in \mathbb {H} )}$

entsteht auf Seite der Zetafunktion eine Funktionalgleichung des Typs^[34]

${\displaystyle \xi (1-s)=\xi (s),}$

wobei ${\displaystyle \xi (s)}$ (Riemannsche Xi-Funktion) bis auf elementare Faktoren, die keine Nullstellen beitragen, genau ${\displaystyle \zeta (s)}$ entspricht. Übertragen auf die komplexe Ebene bedeutet dies „im Wesentlichen“ eine Spiegelung der Zetafunktion entlang der Geraden ${\displaystyle \mathrm {Re} (s)={\tfrac {1}{2}}}$, denn es gilt

${\displaystyle {\frac {1}{2}}=1-{\frac {1}{2}}.}$

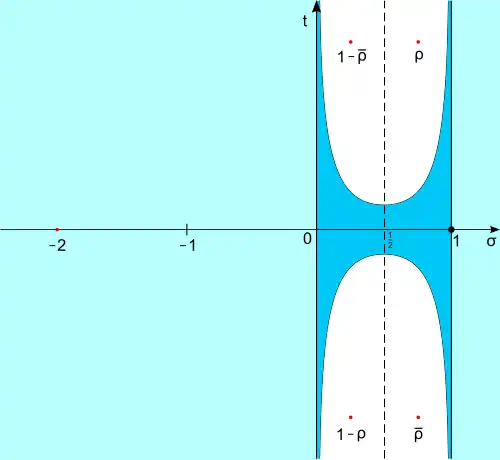
Damit sagt die Modularität der Thetafunktion etwas über Primzahlen aus: Diese können nicht beliebig gleichmäßig (im Extremfall etwa im Sinne 1, 2, 3, 4, …) verteilt sein. Dahinter steckt, dass Nullstellen mit einem kleinen Realteil die Primzahlen nur „wenig beeinflussen“, mit einem großen Realteil aber „stark beeinflussen“. Nun erzwingt die Symmetrie ${\displaystyle s\mapsto 1-s}$ aber, dass zu jeder Nullstelle mit „wenig Einfluss“ eine Nullstelle mit „viel Einfluss“ korrespondiert, denn je kleiner der Realteil von ${\displaystyle s}$, desto größer der von ${\displaystyle 1-s}$, und umgekehrt (siehe Bild).^[35] Die bis heute unbewiesene Riemannsche Vermutung sagt den optimalen Kompromiss voraus: Alle Nullstellen von ${\displaystyle \xi (s)}$ liegen auf der Geraden

${\displaystyle \{\mathrm {Re} (s)={\tfrac {1}{2}}\}}$

womit das „optimalste Verteilungsmuster“ unter den Primzahlen gelten sollte.^[36] Mit anderen Worten: Die „Intensität“ der Nullstellen verändert sich unter der Spiegelung nicht. Wäre etwa ${\displaystyle s={\tfrac {1}{3}}+i}$ Nullstelle, so wegen der Funktionalgleichung auch ${\displaystyle s={\tfrac {2}{3}}-i}$, und dies ist „schlimmer“ als zum Beispiel ${\displaystyle {\tfrac {1}{2}}+i}$. Zusammenfassend: Die Modularität von ${\displaystyle \theta (z)}$ induziert eine „untere Barriere“ für die Gleichmäßigkeit in der Verteilung der Primzahlen^[37] – und die Riemannsche Vermutung besagt, dass diese Barriere gleichzeitig die „obere“ ist.^[36]

Es ist dieses Zusammenspiel aus Symmetrie („Modularität“) und Primzahlen, das die Zahlentheorie bis heute maßgeblich beeinflusst.

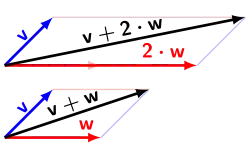
Um die Idee eines Vektorraums zu verstehen, reicht es, an die gewohnte Ebene zu denken. Jeder Punkt ${\displaystyle (x,y)}$ kann auch als „Pfeil“ vom Ursprung aus aufgefasst werden. Diese Pfeile kann man zusammenlegen: Setzt man die Spitze des einen an den Fuß des anderen, ergibt sich ein neuer Pfeil – das ist die Vektoraddition. Ebenso kann man Pfeile verlängern oder verkürzen, indem man sie mit einer Zahl multipliziert. Ist die Zahl negativ, zeigt der Pfeil in die entgegengesetzte Richtung.

Alle Pfeile in der Ebene zusammen, mit diesen beiden Operationen, bilden das, was Mathematiker einen Vektorraum nennen. Die Grundidee ist also: Es existiert eine Sammlung von „Richtungen mit Länge“, und man kann sie kombinieren und skalieren. Die genaue algebraische Definition ist nur eine Abstraktion dieses einfachen Bildes.

Ein besonders hilfreiches Prinzip ist das der Basis. In der Ebene genügen schon zwei Pfeile, etwa ${\displaystyle (1,0)}$ (nach rechts) und ${\displaystyle (0,1)}$ (nach oben), um jeden anderen Pfeil darzustellen – und das sogar eindeutig. Will man z. B. den Pfeil ${\displaystyle (3,2)}$, so kombiniert man drei Schritte nach rechts und zwei Schritte nach oben:

${\displaystyle (3,2)=3\cdot (1,0)+2\cdot (0,1).}$

Diese beiden Basisvektoren sind so etwas wie die „Bausteine“ des gesamten Raums.

Die Anzahl der Pfeile, die man minimal benötigt, um alle anderen zu beschreiben, nennt man die Dimension. Für die Ebene sind es zwei, für den Raum drei. Das Konzept funktioniert auch in viel höheren Dimensionen, die man sich nicht mehr geometrisch vorstellen kann, die aber nach denselben Regeln aufgebaut sind. Die Dimension zählt also gewissermaßen die „Anzahl der Freiheitsgrade“ eines Vektorraums: Wie viele Punkte braucht es, um alle anderen zu erzeugen.

Auch ganze Modulformen zu einem festen Gewicht bilden einen Vektorraum, da sich Funktionen ebenso wie Punkte addieren lassen. Für die Zahlentheorie von großer Bedeutung ist, dass die Vektorräume der ganzen Modulformen endlichdimensional sind. Also reichen stets endlich viele Modulformen (eines festen Gewichts) aus, um alle anderen (desselben Gewichts) durch Linearkombinationen zu erzeugen. Interessant daran ist, dass Modulformen (scheinbar) aus unendlich vielen Informationen aufgebaut sind, nämlich ihren Fourier-Koeffizienten

${\displaystyle f(z)=\sum _{n=0}^{\infty }a_{n}e^{2\pi inz}.}$

Dies bietet eine aus mathematischer Sicht äußerst ungewöhnliche Möglichkeit, das Problem der Unendlichkeit zu umgehen: Eine Übereinstimmung endlich vieler Koeffizienten reicht aus, damit alle anderen Koeffizienten auch übereinstimmen.

Die Anfänge der Theorie gehen auf Carl Friedrich Gauß zurück, der Transformationen spezieller Modulformen unter der Modulgruppe im Rahmen seiner Theorie des arithmetisch-geometrischen Mittels im Komplexen betrachtete (ein Fundamentalbereich zu ${\displaystyle \Gamma (2)}$ findet sich in seinen Aufzeichnungen schon 1805).^[38] Begründer der klassischen (rein analytischen) Theorie der Modulformen des 19. Jahrhunderts sind Richard Dedekind, Felix Klein, Leopold Kronecker, Karl Weierstraß, Carl Gustav Jacobi, Gotthold Eisenstein und Henri Poincaré. Ein bekanntes Beispiel für die Anwendung von Modulformen in der Zahlentheorie war der Satz von Jacobi (Anzahl der Darstellungen einer Zahl durch vier Quadrate). Die moderne Theorie der Modulformen entstand in der ersten Hälfte des 20. Jahrhunderts durch Erich Hecke und Carl Ludwig Siegel, die Anwendungen in der Zahlentheorie verfolgten. Hier spielt die Theorie der Hecke-Operatoren, die im Raum der Modulformen wirken, und mit ihnen definierter Dirichletreihen (Hecke L-Reihe) eine besondere Rolle. Modulformen in Termen der Darstellungstheorie stammen von Robert Langlands (Langlands-Programm). p-adische Modulformen treten zuerst bei Nicholas Katz und Jean-Pierre Serre auf. Modulformen spielten auch eine zentrale Rolle im Beweis der Vermutung von Fermat (Modularitätssatz, der wiederum ein Spezialfall der 2006 bewiesenen Serre-Vermutung ist), die Modulformen mit Galoisdarstellungen der absoluten Galoisgruppe von Zahlkörpern verbindet. Sowohl beim Beweis der Lösung des Gaußschen Klassenzahlproblems durch Kurt Heegner als auch des letzten Teils der Weil-Vermutungen (Riemann-Hypothese) und damit verbunden der Ramanujan-Vermutung durch Pierre Deligne spielten Modulformen eine wichtige Rolle wie auch beim Beweis von Maryna Viazovska (2016), dass das E8-Gitter in acht Dimensionen und das Leech-Gitter in 24 Dimensionen dichteste Kugelpackungen liefern (die Thetafunktionen dieser beiden Gitter sind Modulformen, siehe unten). Modulformen kodieren häufig arithmetische Informationen der algebraischen Zahlkörper, sind aber viel einfacher rechnerisch zugänglich, teilweise schon mit Computeralgebra-Programmen, und die Anzahl linear unabhängiger Modulformen bestimmten Typs ist beschränkt.

Es werden die folgenden üblichen Notationen verwendet:

• ${\displaystyle \mathbb {N} =\{1,2,3,\ldots \}}$ für die natürlichen Zahlen.
• ${\displaystyle \mathbb {Z} =\{\ldots ,-2,-1,0,1,2,3,\ldots \}}$ für die ganzen Zahlen.
• ${\displaystyle \mathbb {Q} }$ für die rationalen Zahlen.
• ${\displaystyle \mathbb {R} }$ für die reellen Zahlen.
• ${\displaystyle \mathbb {C} }$ für die komplexen Zahlen. Es bezeichnen ${\displaystyle \mathrm {Re} (z)}$ und ${\displaystyle \mathrm {Im} (z)}$ den Real- bzw. Imaginärteil der komplexen Zahl ${\displaystyle z}$.
• Es bedeutet ${\displaystyle x\in M}$, dass ${\displaystyle x}$ ein Element der Menge ${\displaystyle M}$ ist, und ${\displaystyle x\notin M}$ dass es kein Element der Menge ${\displaystyle M}$ ist. Zum Beispiel ist ${\displaystyle -{\tfrac {1}{3}}\in \mathbb {Q} }$ und ${\displaystyle -{\tfrac {1}{3}}\notin \mathbb {Z} }$.
• Es bezeichnet ${\displaystyle e^{x}}$ die natürliche Exponentialfunktion und ${\displaystyle \log(x)}$ den natürlichen Logarithmus.

Es sei

${\displaystyle \mathbb {H} :=\{z\in \mathbb {C} \;\;\colon \;\;\mathrm {Im} (z)>0\}}$

die obere Halbebene, d. h. die Menge aller komplexen Zahlen mit positivem Imaginärteil. Es ist aus der klassischen Funktionentheorie bekannt, dass die Gruppe ${\displaystyle {\text{SL}}_{2}(\mathbb {R} )}$ via Möbiustransformation auf ${\displaystyle \mathbb {H} }$ operiert. Dabei werden, wie bei einer Gruppenoperation üblich, die Elemente ${\displaystyle M\in {\text{SL}}_{2}(\mathbb {R} )}$ als Abbildungen ${\displaystyle \mathbb {H} \to \mathbb {H} }$ aufgefasst. Man setzt:

${\displaystyle {\begin{pmatrix}a&b\\c&d\end{pmatrix}}(z):={\frac {az+b}{cz+d}}.}$

Über Möbiustransformation kann damit eine Aktion auf dem Vektorraum der auf ganz ${\displaystyle \mathbb {H} }$ meromorphen bzw. holomorphen Funktionen auf ${\displaystyle \mathbb {H} }$ definiert werden. Dafür wird ein ${\displaystyle k\in \mathbb {Z} }$ fixiert. Man definiert dann den Peterssonschen Strichoperator durch

${\displaystyle f|_{k}M(z):=(cz+d)^{-k}f\left({\frac {az+b}{cz+d}}\right)=(cz+d)^{-k}f(M(z)),\qquad M:={\begin{pmatrix}a&b\\c&d\end{pmatrix}}.}$

Offenbar ist dann ${\displaystyle f|_{k}M}$ wieder holomorph bzw. meromorph auf der oberen Halbebene. Es gilt zudem für alle ${\displaystyle M,N\in {\text{SL}}_{2}(\mathbb {R} )}$ die Rechenregel

${\displaystyle (f|_{k}M)|_{k}N=f|_{k}(MN),}$

womit der Peterssonsche Strichoperator eine Operation auf dem Raum der meromorphen bzw. holomorphen Funktionen auf der oberen Halbebene definiert.^[39]

Jede holomorphe und zugleich 1-periodische Funktion auf der oberen Halbebene besitzt eine Fourier-Entwicklung

${\displaystyle f(z)=\sum _{n=-\infty }^{\infty }a_{n}e^{2\pi izn}}$

mit irgendwelchen komplexen Koeffizeinten ${\displaystyle a_{n}}$, die eindeutig bestimmt sind. In diesem Kontext ist es üblich, ${\displaystyle q:=e^{2\pi iz}}$ zu definieren, und abkürzend

${\displaystyle f(z)=\sum _{n=-\infty }^{\infty }a_{n}q^{n}}$

zu schreiben. Ist ${\displaystyle f}$ lediglich meromorph in ${\displaystyle \mathbb {H} }$, besitzt in ${\displaystyle i\infty }$ jedoch keine Häufung an Polstellen, ist also holomorph auf einer Halbebene ${\displaystyle \mathbb {H} _{r_{0}}:=\{z\in \mathbb {H} \colon \mathrm {Im} (z)>r_{0}\}}$ für ein ${\displaystyle r_{0}>0}$, so kann auf jener eingeschränkten Halbebene ${\displaystyle \mathbb {H} _{r_{0}}}$ wiederum eine Fourier-Reihe oberen Typs angegeben werden.^[40]

Die volle Modulgruppe^[41][14] oder gelegentlich einfach nur Modulgruppe ist definiert durch^[42]

${\displaystyle {\text{SL}}_{2}(\mathbb {Z} ):=\left\{{\begin{pmatrix}a&b\\c&d\end{pmatrix}}\in \mathbb {Z} ^{2\times 2}\;\;\colon \;\;ad-bc=1\right\}.}$

Es handelt sich also um die Kollektion aller ${\displaystyle 2\times 2}$-Matrizen mit ganzen Einträgen, deren Determinante gleich 1 ist. Jede Matrix in der vollen Modulgruppe hat also eine ebenfalls ganzzahlige Inverse mit Determinante 1. Offenbar ist sie eine echte Untergruppe von ${\displaystyle {\text{SL}}_{2}(\mathbb {R} )}$. Sie wird durch die Matrizen

${\displaystyle S={\begin{pmatrix}0&-1\\1&0\end{pmatrix}},\qquad T={\begin{pmatrix}1&1\\0&1\end{pmatrix}}}$

erzeugt.^[43] Diese Matrizen beschreiben geometrisch eine Spiegelung an einem Kreis (Inversion) und eine Translation.^[44]

Manche Autoren bezeichnen auch die projektive spezielle lineare Gruppe ${\displaystyle \mathrm {PSL} _{2}(\mathbb {Z} )}$ als volle Modulgruppe, in der Matrizen ${\displaystyle M}$ und ${\displaystyle -M}$ identifiziert werden. Sie ist der Quotient von ${\displaystyle {\text{SL}}_{2}(\mathbb {Z} )}$ nach ihrem Zentrum ${\displaystyle \{\pm I_{2}\}}$ und der Einheitsmatrix ${\displaystyle I_{2}}$.^[44]

Für eine ganze Zahl ${\displaystyle k}$ heißt eine holomorphe bzw. meromorphe Funktion ${\displaystyle f}$ auf der oberen Halbebene eine ganze (d. h. holomorphe) bzw. meromorphe^[45] elliptische^[46] Modulform vom Gewicht ${\displaystyle k}$ zur Gruppe ${\displaystyle {\mbox{SL}}_{2}(\mathbb {Z} )}$, wenn sie folgende Eigenschaften erfüllt:^[47]

1. Sie ist invariant unter dem Peterssonschen Strichoperator bezüglich ${\displaystyle k}$, also ${\displaystyle f|_{k}M=f}$ für alle ${\displaystyle M\in {\mbox{SL}}_{2}(\mathbb {Z} )}$. Äquivalent gelten simultan die Funktionalgleichungen

${\displaystyle f\!\left({\frac {az+b}{cz+d}}\right)=(cz+d)^{k}f(z)}$ für alle ${\displaystyle z\in \mathbb {H} }$ und ${\displaystyle a,b,c,d\in \mathbb {Z} }$ mit ${\displaystyle ad-bc=1.}$

Insbesondere gilt mit der Wahl ${\displaystyle M=T={\begin{pmatrix}1&1\\0&1\end{pmatrix}}}$ stets ${\displaystyle f(z+1)=f(z)}$.

2. Sie ist „holomorph bzw. meromorph im Unendlichen“. Das bedeutet, dass sie für alle ${\displaystyle z}$ mit hinreichend großem Imaginärteil in eine Fourier-Reihe von der Form

${\displaystyle f(z)=\sum _{n=-n_{0}}^{\infty }a_{n}(f)q^{n}}$

mit einem ${\displaystyle n_{0}\in \mathbb {N} _{0}}$ entwickelbar ist, wobei im holomorphen Fall sogar ${\displaystyle n_{0}=0}$ gewählt werden kann und die betroffene Fourier-Reihe auf der gesamten oberen Halbebene konvergiert. Es ist zweckmäßig, auch im Falle von Referenz auf die Koeffizieten, die Abhängigkeit von ${\displaystyle f}$ hervorzuheben, also ${\displaystyle a_{n}=a_{n}(f)}$.

Eine Modulform von Gewicht ${\displaystyle k=0}$ nennt man auch Modulfunktion.^[48] Modulfunktionen haben ein besonders einfaches Verhalten unter der Modulgruppe, da der Faktor ${\displaystyle (cz+d)^{0}=1}$ entfällt:

${\displaystyle f\left({\frac {az+b}{cz+d}}\right)=f(z).}$

Verschwindet eine ganze Modulform im Unendlichen ${\displaystyle \mathrm {Im} (z)\to \infty }$ (in der Spitze, englisch cusp, ${\displaystyle q=0}$), so nennt man sie Spitzenform.^[49] Aus der Definition folgt, dass eine Modulform für ungerades ${\displaystyle k}$ identisch verschwindet.^[50]

Das Verhalten der Modulform vom Gewicht ${\displaystyle k}$ unter diesen Erzeugenden ist

${\displaystyle f\left(-{\frac {1}{z}}\right)=z^{k}f(z),\qquad f(z+1)=f(z)}$

und aus letzterer Gleichung ergibt sich, dass die Modulform periodisch ist. Daher ist die Fourierentwicklung ${\displaystyle {\tilde {f}}(q)}$ für ${\displaystyle 0<|q|<1}$ wohldefiniert und holomorph bzw. meromorph. Mit den Fourierkoeffizienten ${\displaystyle a_{n}}$ hat man die Fourierreihe (auch q-Entwicklung genannt)

${\displaystyle f(z)=\sum _{n=-m}^{\infty }a_{n}(f)e^{2i\pi nz}=\sum _{n=-m}^{\infty }a_{n}(f)q^{n}}$,

wobei ${\displaystyle m}$ die Ordnung des Pols von ${\displaystyle f}$ in der Spitze ${\displaystyle q=0}$ genannt wird (Imaginärteil von ${\displaystyle z}$ gegen Unendlich). Die Modulform ist bei negativen Fouriergliedern meromorph in der Spitze. Bei einer Spitzenform verschwindet ${\displaystyle f}$ bei ${\displaystyle q=0}$ (${\displaystyle a_{0}(f)=0}$), das heißt, die nichtverschwindenden Fourierkoeffizienten beginnen bei einem positiven ${\displaystyle n}$, das dann Ordnung der Nullstelle von ${\displaystyle f}$ in der Spitze genannt wird.

In der komplexen Ebene ist eine Modulform durch ihre Werte im Fundamentalbereich ${\displaystyle \mathbb {H} /\Gamma }$ definiert, der in der nebenstehenden Abbildung grau gefärbt ist. Er ist ein Dreieck mit einer Spitze im Unendlichen. Jedes der durch Geraden oder Kreise begrenzten fundamentalen Dreiecke entsteht durch Anwendung von Operationen der Modulgruppe auf den Fundamentalbereich. Die Anwendung der Modulgruppe lässt sich beliebig fortsetzen und ergibt eine immer feinere Einteilung, die aber in der Abbildung an einem bestimmten Punkt abgebrochen wurde.

Statt für ${\displaystyle \mathrm {SL} _{2}(\mathbb {Z} )}$ werden Modulformen auch für bestimmte Untergruppen dieser Gruppe betrachtet, insbesondere für die sogenannten Kongruenzuntergruppen der vollen Modulgruppe (${\displaystyle N}$ ist eine positive ganze Zahl):

${\displaystyle \Gamma _{0}(N)=\left\{{\begin{pmatrix}a&b\\c&d\end{pmatrix}}\in \mathrm {SL} _{2}(\mathbb {Z} )\;\;\colon \;\;c\equiv 0{\pmod {N}}\right\}}$

${\displaystyle \Gamma (N)=\left\{{\begin{pmatrix}a&b\\c&d\end{pmatrix}}\in \mathrm {SL} _{2}(\mathbb {Z} )\;\;\colon \;\;c\equiv b\equiv 0{\pmod {N}},\quad a\equiv d\equiv 1{\pmod {N}}\right\}}$

Die Zahl ${\displaystyle N}$ heißt die Stufe der zugeordneten Modulformen. ${\displaystyle \Gamma (N)}$ heißt auch die Hauptkongruenzgruppe der Stufe ${\displaystyle N}$. Jede Untergruppe von ${\displaystyle \mathrm {SL} _{2}(\mathbb {Z} )}$, die die Hauptkongruenzgruppe für eine Stufe ${\displaystyle N}$ als Untergruppe enthält, wird Kongruenzuntergruppe genannt.

Bisweilen betrachtet man auch die Kongruenzuntergruppe

${\displaystyle \Gamma _{1}(N)=\left\{{\begin{pmatrix}a&b\\c&d\end{pmatrix}}\in \mathrm {SL} _{2}(\mathbb {Z} )\;\;\colon \;\;a\equiv d\equiv 1{\pmod {N}},\quad c\equiv 0{\pmod {N}}\right\},}$

die eine Mittelstellung einnimmt zwischen ${\displaystyle \Gamma _{0}}$ (modulo ${\displaystyle N}$ äquivalent zu oberer Dreiecksmatrix) und ${\displaystyle \Gamma }$ (modulo ${\displaystyle N}$ äquivalent zur Einheitsmatrix). Es gilt

${\displaystyle \Gamma (N)\subseteq \Gamma _{1}(N)\subseteq \Gamma _{0}(N)\subseteq \mathrm {SL} _{2}(\mathbb {Z} )}$

und

${\displaystyle \Gamma (1)=\Gamma _{1}(1)=\Gamma _{0}(1)=\mathrm {SL} _{2}(\mathbb {Z} )}$.

Der Index der Kongruenzuntergruppen als Untergruppen von ${\displaystyle \mathrm {SL} _{2}(\mathbb {Z} )}$ ist endlich und lässt sich explizit angeben. So ist:

${\displaystyle \left[\,\mathrm {SL} _{2}(\mathbb {Z} )\colon \Gamma _{0}(N)\,\right]=N\prod _{p\mid N}\left(1+{\frac {1}{p}}\right)}$

${\displaystyle \left[\,\Gamma _{0}(N)\colon \Gamma (N)\,\right]=N^{2}\prod _{p\mid N}\left(1-{\frac {1}{p}}\right)}$

Die Modulformen zu den Kongruenzuntergruppen ${\displaystyle \Gamma _{0}}$ und ${\displaystyle \Gamma _{1}}$ haben Fourierentwicklungen in ${\displaystyle q}$; die von ${\displaystyle \Gamma (N)}$ für ${\displaystyle N\geq 2}$ nicht unbedingt, da die Matrix (${\displaystyle a=d=1,b=1,c=0}$) in der Transformationsmatrix nicht dazugehört (sie haben eine Fourierentwicklung in ${\displaystyle q^{1/N}}$). Es lässt sich aber immer zu einer Modulform für ${\displaystyle \Gamma (N)}$ eine solche für ${\displaystyle \Gamma _{1}(N^{2})}$ zuordnen (die eine Fourierentwicklung in ${\displaystyle q}$ hat). Auch gibt es für Kongruenzuntergruppen kein so einfaches Kriterium für Spitzenformen (der konstante Fourierterm muss nicht unbedingt verschwinden wie bei der vollen Modulgruppe). Neben Modulformen mit Transformationsverhalten wie bei der vollen Modulgruppe diskutiert werden auch solche mit erweitertem Transformationsverhalten (Multiplikation mit einem Dirichlet-Charakter) betrachtet.

Mit diesen Kongruenzuntergruppen kann man die Quotientenräume wie ${\displaystyle H\backslash \Gamma (N)=Y(N)}$ bilden, die durch Hinzunahme endlich vieler Punkte (Cusps, Spitzen der Kongruenzuntergruppe) in der erweiterten oberen Halbebene^[51] ${\displaystyle H^{*}}$ kompaktifiziert werden, der entsprechende kompaktifizierte Quotientenraum heißt dann ${\displaystyle X(N)}$. Entsprechend spricht man bei der Kongruenzuntergruppe ${\displaystyle \Gamma _{0}(N)}$ von ${\displaystyle Y_{0}(N)}$ bzw. ${\displaystyle X_{0}(N)}$ und bei ${\displaystyle \Gamma _{1}(N)}$ von ${\displaystyle Y_{1}(N),X_{1}(N)}$. Nach Kompaktifizierung erhält man kompakte Riemannsche Flächen unterschiedlichen topologischen Geschlechts ${\displaystyle g}$. Die verschiedenen ${\displaystyle X,Y}$ heißen auch Modulkurven.

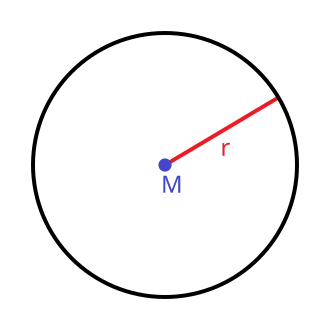
Die Idee eines Modulraumes ist, Objekte aus der Geometrie („Moduln“) als „Punkte in einem Raum“ zu interpretieren, um im Anschluss diesen Raum als Ganzes zu studieren, in der Hoffnung, Informationen über die geometrischen Objekte zu erhalten. Dieses abstrakte Konzept lässt sich an einem elementaren Beispiel verdeutlichen: dem Raum aller Kreise in der Ebene. Jeder Kreis wird durch zwei Daten bestimmt: seinen Mittelpunkt ${\displaystyle (x,y)\in \mathbb {R} ^{2}}$ und seinen Radius ${\displaystyle r\geq 0}$, obwohl (außer im pathologischen Fall ${\displaystyle r=0}$) ein Kreis aus unendlich vielen Punkten besteht. Hintergrund ist die starke geometrische Struktur eines Kreises. Damit erhält man eine Parametrisierung

${\displaystyle \{{\text{Kreise in der Ebene}}\}\;\cong \;\{{\text{Punkte in der Ebene}}\}\times \{{\text{Radien}}\}\;\cong \;\mathbb {R} ^{2}\times \mathbb {R} _{\geq 0}.}$ (Mittelpunkte werden mit Radien gepaart)

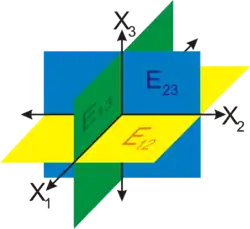
Dieser Raum ${\displaystyle \mathbb {R} ^{2}\times \mathbb {R} _{\geq 0}}$ ist der Modulraum der Kreise: Jedes Element entspricht genau einem Kreis, und umgekehrt. Man nennt ihn einen Modulraum, weil er die Menge der Objekte (Kreise) nicht nur als lose Sammlung betrachtet, sondern sie in eine geometrische Struktur einbettet, die zusätzliche Operationen wie Abstände oder Deformationen erlaubt. Im Falle der Kreise ist der Modulraum in eine dreidimensionale Struktur eingebettet (siehe Bild).

Modulräume haben nützliche Anwendungen. Ein naheliegender nächster Schritt ist die Einführung einer Metrik auf dem Modulraum der Kreise, also einer Art „Abstandsfunktion“ zwischen zwei Kreisen. Dadurch kann man quantitativ beschreiben, „wie verschieden“ zwei Kreise sind. Ein einfaches Modell wäre, den Abstand zweier Kreise ${\displaystyle C_{1}=(x_{1},y_{1},r_{1})}$ und ${\displaystyle C_{2}=(x_{2},y_{2},r_{2})}$ in ${\displaystyle \mathbb {R} ^{2}\times \mathbb {R} _{\geq 0}}$ durch den euklidischen Abstand dieser Parameter zu definieren:

${\displaystyle d(C_{1},C_{2}):={\sqrt {(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}+(r_{1}-r_{2})^{2}}}.}$

In diesem Sinn misst die Metrik die Unterschiede in den Mittelpunkten und im Radius. Je kleiner der Abstand, desto ähnlicher sind sich die beiden Kreise. Dies macht deutlich, dass der Modulraum nicht nur die Gesamtheit der Objekte beschreibt, sondern zugleich eine natürliche Geometrie trägt, in der man Variationen und Verformungen präzise fassen kann. Ein besonders wichtiges Prinzip – auch im Kontext von Modulformen – ist, dass die Beschreibung aller Kreise durch einen Modulraum, der in einem dreidimensionalen Gebilde ${\displaystyle \mathbb {R} ^{3}}$ liegt, ermöglicht, differenzierbare Funktionen

${\displaystyle f\colon \{{\text{Kreise in der Ebene}}\}\to \mathbb {C} }$

zu betrachten, da auf Räumen wie ${\displaystyle \mathbb {R} ^{3}}$ (höherdimensionale) Differentialrechnung betrieben werden kann. Ein solches ${\displaystyle f}$ ist in diesem Sinne bereits eine „Modulfunktion“ (auch wenn der Begriff nicht Kreisen vorbehalten ist!), also eine Funktion, die als Eingabe Moduln entgegennimmt, aber gleichzeitig auch schöne analytische Eigenschaften hat.

Genau dieses Prinzip überträgt die Theorie der Modulräume auf wesentlich kompliziertere Objekte, etwa elliptische Kurven oder Vektorbündel: Man fasst sie alle zusammen in einen Raum, der ihre Parameter (die „Moduln“) organisiert, und stattet diesen Raum mit geometrischen, algebraischen und analytischen Strukturen aus, um die Vielfalt und Unterschiede der Objekte systematisch zu untersuchen.

Bei elliptischen Kurven handelt es sich um eine Ansammlung von Punkten ${\displaystyle (x,y)}$, die gemeinsam eine kubische Gleichung erfüllen, die meist in der Form

${\displaystyle y^{2}=x^{3}+ax^{2}+bx+c}$ mit festen Zahlen ${\displaystyle a,b,c}$

geschrieben wird.^{[Anm. 1]} Die Zahlen ${\displaystyle a,b}$ und ${\displaystyle c}$ sind rational, und wegen deren Beliebigkeit^{[Anm. 2]} gibt es eine „unendliche Familie“ elliptischer Kurven:

${\displaystyle y^{2}=x^{3}+x^{2}-x}$

${\displaystyle y^{2}=x^{3}-{\tfrac {1}{2}}x^{2}+3x+1}$

${\displaystyle y^{2}=x^{3}+{\tfrac {11}{134}}x-{\tfrac {1}{5}}}$

und eine unbegrenzte Zahl weiterer Beispiele.

Die moderne Definition von Modulformen zur vollen Modulgruppe lässt sich elegant aus der Theorie komplexer Gitter und elliptischer Kurven herleiten. Ein (komplexes) Gitter ist eine diskrete Untergruppe der Form

${\displaystyle L=\omega _{1}\mathbb {Z} +\omega _{2}\mathbb {Z} \subset \mathbb {C} \quad }$ mit ${\displaystyle \quad {\frac {\omega _{1}}{\omega _{2}}}\notin \mathbb {R} }$.

Aus Gründen der Orientierung macht es Sinn, ohne Beschränkung der Allgemeinheit ${\displaystyle {\tfrac {\omega _{1}}{\omega _{2}}}\in \mathbb {H} }$ fordern. Der Quotient ${\displaystyle \mathbb {C} /L}$ ist eine komplexe Torusfläche. Über die Weierstraß’sche ${\displaystyle \wp }$-Funktion erhält man eine Einbettung in die projektive Ebene, die zeigt, dass jeder solche Torus als glatte kubische Kurve geschrieben werden kann:

${\displaystyle y^{2}=4x^{3}-g_{2}(L)\,x-g_{3}(L).}$

Die Koeffizienten ${\displaystyle g_{2},g_{3}}$ sind aus den Gitter-Summen der Weierstraß’schen Invarianten definiert,^[52]

${\displaystyle g_{2}(L)=60\!\!\sum _{\omega \in L\setminus \{0\}}\!\!\omega ^{-4},\qquad g_{3}(L)=140\!\!\sum _{\omega \in L\setminus \{0\}}\!\!\omega ^{-6},}$

und hängen nur von der Homotheteklasse des Gitters ab. Das Diskriminantenkriterium ${\displaystyle \Delta _{\text{alg}}(L)=g_{2}(L)^{3}-27g_{3}(L)^{2}\neq 0}$ charakterisiert die Glattheit der Kurve.^[53]

Wählt man eine geordnete Basis ${\displaystyle \{\omega _{1},\omega _{2}\}}$, so ist der zugehörige Modulparameter ${\displaystyle \tau ={\tfrac {\omega _{1}}{\omega _{2}}}\in \mathbb {H} }$ wohldefiniert bis zur Wirkung der vollen Modulgruppe. Denn ein Basiswechsel

${\displaystyle {\begin{pmatrix}\omega _{1}'\\\omega _{2}'\end{pmatrix}}={\begin{pmatrix}a&b\\c&d\end{pmatrix}}\!{\begin{pmatrix}\omega _{1}\\\omega _{2}\end{pmatrix}},\qquad {\begin{pmatrix}a&b\\c&d\end{pmatrix}}\in \mathrm {SL} _{2}(\mathbb {Z} ),}$

transformiert den Parameter durch eine Möbius-Transformation^[14]

${\displaystyle \tau '={\frac {a\tau +b}{c\tau +d}}.}$

Dadurch parametrisiert die obere Halbebene ${\displaystyle \mathbb {H} =\{\tau \in \mathbb {C} :\operatorname {Im} \tau >0\}}$ die Homotheteklassen von Gittern (und damit komplexe elliptische Kurven), modulo der Wirkung von ${\displaystyle \mathrm {SL} _{2}(\mathbb {Z} )}$.

Aus Gitter-Sicht ist eine (holomorphe) Modulform vom Gewicht ${\displaystyle k}$ eine Funktion ${\displaystyle F}$ auf der Menge der Gitter mit den Homogenitäts- und Invarianzeigenschaften

${\displaystyle F(\lambda L)=\lambda ^{-k}F(L)\quad (\lambda \in \mathbb {C} ^{\times }),\qquad F(L)=F(L')\ {\text{falls}}\ L\cong L'.}$

Analytisch entspricht dies einer holomorphen Funktion ${\displaystyle f:\mathbb {H} \to \mathbb {C} }$ mit Transformationsgesetz

${\displaystyle f\!\left({\frac {a\tau +b}{c\tau +d}}\right)=(c\tau +d)^{k}\,f(\tau )\qquad {\text{für alle }}{\begin{pmatrix}a&b\\c&d\end{pmatrix}}\in \mathrm {SL} _{2}(\mathbb {Z} ).}$

Dabei ist die Variable ${\displaystyle \tau }$ statt ${\displaystyle z}$ bei der Betonung des Gitterkontextes üblich.^[54] Die Homhomogenität rührt daher, dass die kanonische holomorphe Differentialform auf ${\displaystyle \mathbb {C} /L}$ durch Skalierung ${\displaystyle z\mapsto \lambda z}$ um den Faktor ${\displaystyle \lambda ^{-1}}$ mittransformiert; eine Gewicht-${\displaystyle k}$-Form ist invariant, wenn man gleichzeitig diese natürliche Skalierung ${\displaystyle k}$-fach berücksichtigt. Geometrisch sind Modulformen genau die globalen Schnitte von Potenzen des Hodge-Bündels auf der Modulkategorie der elliptischen Kurven; Spitzenformen sind diejenigen Schnitte, die an der Randstelle (der Spitze) verschwinden.

Erste nichttriviale Beispiele für elliptische Modulformen sind die sog. Eisensteinreihen, benannt nach Gotthold Eisenstein. Bei deren Konstruktion wird die Modularität durch eine Form der symmetrischen Addition erzwungen.

Für eine ganze, gerade Zahl ${\displaystyle k\geq 4}$ wird die (klassische) Eisensteinreihe vom Gewicht ${\displaystyle k}$ durch die absolut konvergente Reihe^[55]

${\displaystyle G_{k}(z)\;:=\!\!\sum _{(m,n)\in \mathbb {Z} ^{2}\setminus \{(0,0)\}}{\frac {1}{(mz+n)^{k}}}\qquad (z\in \mathbb {H} )}$

definiert. Für ungerades ${\displaystyle k}$ ist die Reihe antisymmetrisch und liefert ${\displaystyle G_{k}\equiv 0}$, weshalb dieser Fall ausgelassen wird. Jedes ${\displaystyle G_{k}}$ definiert eine ganze Modulform des Gewichts ${\displaystyle k}$ zur vollen Modulgruppe. Man hat also ${\displaystyle G_{k}\in {\mathcal {M}}_{k}}$.^[56]

Es ist oft praktisch, die normierte Eisensteinreihe

${\displaystyle E_{k}(z)\;:=\;{\frac {G_{k}(z)}{2\zeta (k)}}}$

zu verwenden; dann hat ${\displaystyle E_{k}}$ konstanten Term 1 in der Fourier-Entwicklung (siehe unten). Hier bezeichnet ${\displaystyle \zeta (s)}$ die Riemannsche Zetafunktion. Es wird jene Normierung mit ${\displaystyle {\tfrac {(k-1)!}{2(2\pi i)^{k}}}}$, sodass der Koeffizient zu ${\displaystyle q}$ gleich 1 wird, gelegentlich ebenfalls als ${\displaystyle E_{k}}$ bezeichnet.^[57]

Es gelten die Fourier-Entwicklungen^[58]

${\displaystyle G_{k}(z)=2\zeta (k)+{\frac {2(2\pi i)^{k}}{(k-1)!}}\,\sum _{n=1}^{\infty }\sigma _{k-1}(n)\,q^{n},}$

und^[59]

${\displaystyle E_{k}(z)=1-{\frac {2k}{B_{k}}}\sum _{n=1}^{\infty }\sigma _{k-1}(n)\,q^{n}}$

wobei ${\displaystyle B_{k}}$ die ${\displaystyle k}$-te Bernoulli-Zahl^[60] bezeichnet und ${\displaystyle \sigma _{a}(n):=\sum _{d|n}d^{a}}$ die Teilerfunktion. Die beiden Formen sind äquivalent über die Relation^[61]

${\displaystyle \zeta (2m)=(-1)^{m+1}{\frac {B_{2m}(2\pi )^{2m}}{2(2m)!}}\qquad (m\in \mathbb {N} ).}$

Entscheidendes Hilfsmittel für die Herleitung der Fourier-Reihen ist die für ${\displaystyle k\geq 2}$ gültige Lipschitz-Formel^[61]

${\displaystyle \sum _{n\in \mathbb {Z} }(n+z)^{-k}={\frac {(-2\pi i)^{k}}{(k-1)!}}\sum _{r=1}^{\infty }r^{k-1}e^{2\pi irz},}$

die mit Hilfe elementarer Methoden der Fourier-Analysis gezeigt werden kann.^[62]

Mit ${\displaystyle B_{4}=-{\tfrac {1}{30}}}$ und ${\displaystyle B_{6}={\tfrac {1}{42}}}$ erhält man beispielsweise^[63]

${\displaystyle E_{4}(z)\;=\;1+240\sum _{n=1}^{\infty }\sigma _{3}(n)\,q^{n}\;=\;1+240\,q+2160\,q^{2}+6720\,q^{3}+17520\,q^{4}+\cdots }$

und

${\displaystyle E_{6}(z)\;=\;1-504\sum _{n=1}^{\infty }\sigma _{5}(n)\,q^{n}\;=\;1-504\,q-16632\,q^{2}-122976\,q^{3}-532728\,q^{4}+\cdots .}$

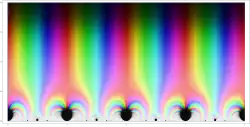
Die beiden wichtigsten klassischen Modulformen zur vollen Modulgruppe – neben den Eisensteinreihen – sind die Diskriminante ${\displaystyle \Delta (z)}$ und die aus ihr gebildete ${\displaystyle j}$-Funktion. Die Diskriminante ist eine Spitzenform vom Gewicht 12 und wird durch die algebraische Relation^[64]

${\displaystyle \Delta (z):={\tfrac {1}{1728}}\,{\big (}E_{4}(z)^{3}-E_{6}(z)^{2}{\big )}}$

definiert, wobei ${\displaystyle E_{4}}$ und ${\displaystyle E_{6}}$ die normierten Eisensteinreihen vom Gewicht 4 bzw. 6 sind. Alternativ lässt sich die unendliche Produktentwicklung

${\displaystyle \Delta (z)=q\,\prod _{n=1}^{\infty }(1-q^{n})^{24}}$

zeigen. Gelegentlich wird diese auch als Definition der Diskriminante herangezogen.^[65] Sie besitzt die Fourier-Entwicklung mit Leitkoeffizient 1:^[66]

${\displaystyle \Delta (z)=\sum _{n=1}^{\infty }\tau (n)q^{n}=q-24\,q^{2}+252\,q^{3}-1472\,q^{4}+4830\,q^{5}-6048\,q^{6}+8405\,q^{7}\,+\cdots ,}$

wobei ${\displaystyle \tau (n)}$ die Ramanujansche tau-Funktion bezeichnet.^[67]

Die ${\displaystyle j}$-Funktion erhält man als Quotient^[68]

${\displaystyle j(z):={\frac {E_{4}(z)^{3}}{\Delta (z)}}.}$

Dies ist eine meromorphe Funktion auf der Modulkurve ${\displaystyle \Gamma \backslash \mathbb {H} }$, invariant unter der vollen Modulgruppe und holomorph auf der oberen Halbebene. Sie ist also eine in der oberen Halbebene holomorphe Modulfunktion bis auf einen einfachen Pol in der Spitze, also ein Beispiel für eine Modulform, die nicht ganz ist.

Trotz sehr zahlreicher Anwendungen stechen einige Entdeckungen und Vermutungen um den Themenkomplex der Modulformen besonders hervor.

Holomorphen Modulformen, und allgemeiner auch gewissen automorphen Formen bzw. Darstellungen, können sog. L-Funktionen zugeordnet werden. Ist die betroffene Modulform eine sog. normalisierte Hecke-Eigenform, so besitzen diese L-Funktionen ein Euler-Produkt. Gleichzeitig impliziert die modulare Symmetrie eine Spiegelung des Abbildungsverhaltens der L-Funktion an einer vertikalen Geraden, der sog. kritischen Geraden. Die Große Riemannsche Vermutung besagt, dass sämtliche nichttriviale Nullstellen dieser L-Funktionen auf dieser kritischen Geraden liegen.^[69] Prototyp ist die Riemannsche Zeta-Funktion, die zur Jacobischen Theta-Funktion, einer Modulform halbganzen Gewichts, korrespondiert. Eine Konsequenz dieser Aussage wäre eine Form der Pseudozufälligkeit in der Verteilung der Primzahlen.^[36] Von einem Beweis dieser Vermutung ist man, selbst im Spezialfall der klassischen Riemannschen Vermutung, noch weit entfernt.

Für die volle Modulgruppe ${\displaystyle \Gamma =\mathrm {SL} _{2}(\mathbb {Z} )}$ wird mit

${\displaystyle f(z)=\sum _{n=1}^{\infty }a_{n}(f)q^{n}}$

eine normierte Hecke-Eigenform vom Gewicht ${\displaystyle k\geq 2}$ (Spitzenform, also ${\displaystyle a_{0}(f)=0}$ und normiert, also ${\displaystyle a_{1}(f)=1}$) betrachtet. Die zugehörige Hecke-L-Funktion ist die Dirichlet-Reihe

${\displaystyle L(f,s):=\sum _{n=1}^{\infty }{\frac {a_{n}(f)}{n^{s}}},\qquad \mathrm {Re} (s)>k.}$

Durch die Multiplikativität der Koeffizienten zerfällt sie in ein Euler-Produkt

${\displaystyle L(f,s)=\prod _{p\,\mathrm {Primzahl} }{\frac {1}{1-a_{p}(f)p^{-s}+p^{k-1-2s}}}.}$

Die Reihe besitzt eine analytische Fortsetzung auf die ganze Ebene und erfüllt eine Funktionalgleichung. Setzt man die vollständig normalisierte L-Funktion

${\displaystyle \Lambda (f,s):=(2\pi )^{-s}\,\Gamma (s)\,L(f,s),}$

so gilt die Symmetrie

${\displaystyle \Lambda (f,s)=(-1)^{\frac {k}{2}}\,\Lambda (f,k-s).}$

Damit ist der kritische Streifen gegeben durch ${\displaystyle \{0<\mathrm {Re} (s)<k\}}$ und die kritische Gerade die Mittellinie ${\displaystyle \{\mathrm {Re} (s)={\tfrac {k}{2}}\}}$. Die nichttrivialen Nullstellen von ${\displaystyle L(f,s)}$ liegen innerhalb dieses Streifens; die sogenannten trivialen Nullstellen außerhalb stammen von den Polstellen der Gammafunktion. Die Große Riemannsche Vermutung (manchmal auch GRH) für ${\displaystyle L(f,s)}$ behauptet, dass alle nichttrivialen Nullstellen auf der kritischen Geraden ${\displaystyle \{\mathrm {Re} (s)={\tfrac {k}{2}}\}}$ liegen. Häufig verschiebt man die Variable zu

${\displaystyle s'=s-{\frac {k-1}{2}}}$,

sodass die Funktionalgleichung eine Invarianz unter

${\displaystyle s'\mapsto 1-s'}$

ausdrückt und die kritische Gerade zu ${\displaystyle \{\mathrm {Re} (s')={\tfrac {1}{2}}\}}$ wird, analog zur klassischen Zetafunktion.^[70]

Im Rahmen einer Kongruenzuntergruppe ${\displaystyle \Gamma _{0}(N)}$ sei

${\displaystyle f(z)=\sum _{n\geq 1}a_{n}(f)\,q^{n}\in {\mathcal {S}}_{k}(\Gamma _{0}(N),\chi )}$

eine normierte neue Hecke-Eigenform (newform) vom Gewicht ${\displaystyle k\geq 2}$ mit Nebentyp (Dirichlet-Charakter) ${\displaystyle \chi {\pmod {N}}}$. Ihre Hecke-L-Funktion ist die Dirichlet-Reihe

${\displaystyle L(f,s)=\sum _{n=1}^{\infty }{\frac {a_{n}(f)}{n^{s}}},\qquad \mathrm {Re} (s)>k.}$

Durch schwache Multiplikativität der Koeffizienten zerlegt sie sich in ein Euler-Produkt. Für ${\displaystyle p\nmid N}$ existieren Parameter ${\displaystyle \alpha _{p},\beta _{p}}$ mit

${\displaystyle \alpha _{p}+\beta _{p}=a_{p}(f),\qquad \alpha _{p}\beta _{p}=\chi (p)\,p^{\,k-1},}$

und

${\displaystyle L(f,s)=\prod _{p\nmid N}{\frac {1}{(1-\alpha _{p}p^{-s})(1-\beta _{p}p^{-s})}}\;\cdot \!\!\prod _{p\mid N}L_{p}(f,s),}$

wobei die lokalen Faktoren ${\displaystyle L_{p}(f,s)}$ an den Stellen ${\displaystyle p\mid N}$ vom Reduktionstyp abhängen.

Die vervollständigte normalisierte L-Funktion lautet

${\displaystyle \Lambda (f,s)=N^{\,{\frac {s}{2}}}\,(2\pi )^{-s}\,\Gamma (s)\,L(f,s),}$

und sie setzt sich meromorph (für Spitzenformen sogar holomorph) auf ganz ${\displaystyle \mathbb {C} }$ fort und erfüllt die Funktionalgleichung

${\displaystyle \Lambda (f,s)=\varepsilon (f)\,i^{-k}\,\Lambda ({\overline {f}},\,k-s),\qquad |\varepsilon (f)|=1,}$

wobei ${\displaystyle \varepsilon (f)}$ die (globale) Wurzelzahl ist und ${\displaystyle {\overline {f}}}$ die komplex konjugierte Eigenform bezeichnet. Im trivialen Nebentyppfall mit reellen Koeffizienten vereinfacht sich dies zu

${\displaystyle \Lambda (f,s)=\varepsilon (f)\,(-1)^{k/2}\,\Lambda (f,\,k-s),\qquad \varepsilon (f)\in \{\pm 1\}.}$

Damit liegt der kritische Streifen bei

${\displaystyle \{0<\mathrm {Re} (s)<k\},}$

und die kritische Gerade ist

${\displaystyle \{\mathrm {Re} (s)={\tfrac {k}{2}}\}.}$

Äquivalent setzt man ${\displaystyle s'=s-{\tfrac {k-1}{2}}}$ und erhält eine Funktionalgleichung ${\displaystyle s'\mapsto 1-s'}$ mit kritischer Geraden ${\displaystyle \{\mathrm {Re} (s')={\tfrac {1}{2}}\}}$.

Diese Aussage verallgemeinert den Spezialfall der vollen Modulgruppe ${\displaystyle \Gamma =\mathrm {SL} _{2}(\mathbb {Z} )}$ (Führer ${\displaystyle N=1}$) auf beliebiges Level ${\displaystyle N}$ und umfasst auch nichttrivialen Nebentyp ${\displaystyle \chi }$ (mit entsprechendem Vorfaktor ${\displaystyle \varepsilon (f)}$ in der Funktionalgleichung). Ein Beweis ist – ebenso wie im Spezialfall der klassischen Riemannschen Vermutung – bislang nicht bekannt.

Die Große Riemannsche Vermutung ist von Bedeutung für die Zahlentheorie, etwa im Umfeld der Theorie der elliptischen Kurven. Im Jahr 2004 konnte Roger Heath-Brown zeigen, dass unter Annahme der Großen Riemannschen Vermutung (für die L-Funktionen elliptischer Kurven) der durchschnittliche analytische Rang der elliptischen Kurven ${\displaystyle y^{2}=x^{3}+Ax+B}$ höchstens 2 sein kann.^[71] Zev Klagsbrun, Travis Sherman und James Weigandt konnten 2019 (Preprint 2016) zeigen, dass unter Annahme der Großen Riemannschen Vermutung der Rang der von Noam Elkies gefundenen elliptischen Kurve

${\displaystyle y^{2}+xy+y\;=\;x^{3}-x^{2}}$

${\displaystyle -\,20067762415575526585033208209338542750930230312178956502\,x}$

${\displaystyle +\,34481611795030556467032985690390720374855944359319180361266008296291939448732243429}$

von Rang mindestens 28 sogar gleich 28 ist.^[72]

Zu Beginn des 20. Jahrhunderts nutzten Godfrey Harold Hardy und Srinivasa Ramanujan die Modularität der Dedekindschen Eta-Funktion, um eine asymptotische Formel für die Partitionsfunktion ${\displaystyle p(n)}$ herzuleiten, nämlich

${\displaystyle p(n)\sim {\frac {1}{4{\sqrt {3}}n}}\,e^{\pi {\sqrt {\tfrac {2n}{3}}}},\quad n\to \infty ,}$

wobei ${\displaystyle \pi =3{,}141\ldots }$ die Kreiszahl und ${\displaystyle e=2{,}718\ldots }$ die Eulersche Zahl bezeichnet.

Die Zahl ${\displaystyle p(n)}$ gibt die Anzahl der Möglichkeiten an, wie man ${\displaystyle n}$ als Summe natürlicher Zahlen darstellen kann, ohne die Reihenfolge der Summanden zu unterscheiden. Beispielsweise gilt ${\displaystyle p(4)=5}$, denn

${\displaystyle {\begin{aligned}4&=4\\&=3+1\\&=2+2\\&=2+1+1\\&=1+1+1+1.\end{aligned}}}$

Hardy und Ramanujan entwickelten hierfür die sogenannte Kreismethode, eine frühe Form der analytischen Zahlentheorie, bei der die Modularität der Dedekindschen Etafunktion entscheidend eingeht. Ihre asymptotische Formel war ein Durchbruch in der Theorie der Partitionen und gilt bis heute als klassisches Beispiel für die Anwendung von Modulformen in der Kombinatorik.

Im Jahr 1937 konnte Hans Rademacher die Methode verfeinern und, erneut mit Hilfe der Modularität, sogar eine exakte Formel für ${\displaystyle p(n)}$ angeben:

${\displaystyle p(n)={\frac {2\pi }{(24n-1)^{\frac {3}{4}}}}\sum _{k=1}^{\infty }{\frac {A_{k}(n)}{k}}I_{\frac {3}{2}}\left({\frac {\pi {\sqrt {24n-1}}}{6k}}\right),}$

wobei

${\displaystyle I_{\frac {3}{2}}(x):={\sqrt {\frac {2}{\pi }}}{\frac {x\cosh(x)-\sinh(x)}{x^{\frac {3}{2}}}}}$

die sog. Bessel-Funktion erster Art ist und

${\displaystyle A_{k}(n):=\sum _{0\leq h<k \atop \gcd(h,k)=1}\exp \left(\pi is(h,k)-{\frac {2\pi inh}{k}}\right)={\frac {1}{2}}{\sqrt {\frac {k}{12}}}\sum _{d{\pmod {24k}} \atop d^{2}\equiv -24n+1{\pmod {24k}}}\left({\frac {12}{d}}\right)\exp \left({\frac {2\pi id}{12k}}\right)}$

mit der Dedekind-Summe

${\displaystyle s(h,k):=\sum _{r=1}^{k-1}{\frac {r}{k}}\left\{{\frac {hr}{k}}\right\}}$

und dem Kronecker-Symbol ${\displaystyle ({\frac {\cdot }{\cdot }})}$. Diese stellt ${\displaystyle p(n)}$ als eine konvergente unendliche Reihe dar, deren Glieder Besselfunktionen und Exponentialterme enthalten. Damit wurde die bis dahin rein asymptotische Theorie auf eine präzise geschlossene Form gebracht.

In der Mathematik bezeichnet ein Körper eine Menge, innerhalb der, einfach gesprochen, mit den vier Grundrechenarten gerechnet werden kann. Dabei sollen die aus der Schulmathematik bekannten Regeln des Kommutativgesetzes (Vertauschbarkeit bei „Plus“ und „Mal“), Assoziativgesetzes (Vertauschbarkeit von Klammern bei „nur Plus“ oder „nur Mal“) und Distributivgesetzes („Ausklammern“ und „Ausmultiplizieren“) gelten. Außerdem muss stets das Element ${\displaystyle 0}$ (neutrales Element der Addition) und ${\displaystyle 1}$ (neutrales Element der Multiplikation) Teil eines Körpers sein. Insbesondere soll durch jede Zahl ungleich der ${\displaystyle 0}$ dividiert werden können. Wichtige Beispiele sind der Körper der reellen Zahlen (Bezeichnung: ${\displaystyle \mathbb {R} }$) oder der Körper der rationalen Zahlen (Bezeichnung: ${\displaystyle \mathbb {Q} }$).

Ganz kurz gesprochen: Ein Körper ${\displaystyle K}$ enthält die Zahlen 0 und 1, und die Mengen ${\displaystyle K}$ und ${\displaystyle K\setminus \{0\}}$ bilden simultan abelsche Gruppen bezüglich der Addition bzw. Multiplikation, wobei diese über das Distributivgesetz miteinander „interagieren“.

Eine wichtige Forderung ist, dass keine der erlaubten Rechenoperationen dazu führt, dass man die den Körper definierende Zahlenmenge verlässt. So ist es etwa in Körpern im Allgemeinen nicht erlaubt, Quadratwurzeln zu ziehen. Es ist ${\displaystyle 2}$ ein Element von ${\displaystyle \mathbb {Q} }$, kurz ${\displaystyle 2\in \mathbb {Q} }$, aber ${\displaystyle {\sqrt {2}}}$ ist eine irrationale Zahl, also ${\displaystyle {\sqrt {2}}\notin \mathbb {Q} }$. Ähnlich besitzt ${\displaystyle -1}$ keine Quadratwurzel in den reellen Zahlen. Grundsätzlich ist das Konzept einer Quadratwurzel in einem Körper aber indirekt erklärt, da die umgekehrte Operation, nämlich die Multiplikation einer Zahl mit sich selbst, in Körpern definiert ist, wobei die Existenz eine andere Frage ist.

Eine Fragestellung aus der Algebra ist, wie Körper aussehen können, also in welchen Typen von Mengen ein „abgeschlossenes Rechnen“ möglich ist. So kann man weitere nichtrationale Zahlen zu ${\displaystyle \mathbb {Q} }$ hinzunehmen, um größere Körper zu konstruieren. Ein Beispiel ist der Körper ${\displaystyle \mathbb {Q} ({\sqrt {2}})}$, der aus allen Zahlen ${\displaystyle x+{\sqrt {2}}y}$ mit ${\displaystyle x,y\in \mathbb {Q} }$ besteht (Quadratischer Zahlkörper).^[73] Rechnungen wie

${\displaystyle (-2+3{\sqrt {2}})+(3-{\sqrt {2}})=1+2{\sqrt {2}},\quad (1-{\sqrt {2}})\cdot (2+{\tfrac {3}{7}}{\sqrt {2}})={\tfrac {8}{7}}-{\tfrac {11}{7}}{\sqrt {2}},\quad {\tfrac {3+{\sqrt {2}}}{4-2{\sqrt {2}}}}=2+{\tfrac {5}{4}}{\sqrt {2}}}$

sind Prototypen für die Abgeschlossenheit der vier Grundrechenarten in ${\displaystyle \mathbb {Q} ({\sqrt {2}})}$. Es ist ${\displaystyle \mathbb {Q} ({\sqrt {2}})}$, zusammen mit ${\displaystyle \mathbb {Q} }$ und ${\displaystyle \mathbb {R} }$, ein weiteres Beispiel für einen Körper mit unendlich vielen Elementen.

Ein Zahlkörper ist ein spezieller Körper, der durch Erweiterung der rationalen Zahlen ${\displaystyle \mathbb {Q} }$ entsteht. Formal bedeutet das: Jeder Zahlkörper ${\displaystyle K}$ ist eine endliche Körpererweiterung von ${\displaystyle \mathbb {Q} }$. Anders gesagt: Man fügt zu den rationalen Zahlen neue Zahlen hinzu (wie ${\displaystyle {\sqrt {2}}}$ oder ${\displaystyle i={\sqrt {-1}}}$), und zwar nur so viele, dass das Resultat noch ein Körper bleibt und zudem ein endlichdimensionaler Vektorraum über ${\displaystyle \mathbb {Q} }$ ist.

Beispiele sind

• ${\displaystyle \mathbb {Q} }$ selbst,
• der quadratische Zahlkörper ${\displaystyle \mathbb {Q} ({\sqrt {2}})}$,
• oder der imaginär-quadratische Zahlkörper ${\displaystyle \mathbb {Q} (i)}$, der alle Gaußschen Zahlen ${\displaystyle a+bi}$ mit rationalen ${\displaystyle a,b}$ enthält.

Zahlkörper sind damit eine natürliche Verallgemeinerung der rationalen Zahlen. Sie spielen in der modernen Zahlentheorie eine zentrale Rolle: Viele Fragestellungen über Primzahlen oder Gleichungen lassen sich in Zahlkörpern präziser formulieren und verstehen. Speziell die imaginär-quadratischen Zahlkörper bilden den Ausgangspunkt für Kroneckers Jugendtraum, da ihre abelschen Erweiterungen über Werte der j-Funktion an Heegner-Punkten beschrieben werden können, siehe unten.

Ein Grundproblem der klassischen Zahlentheorie ist die Beschreibung von Körpererweiterungen: Welche neuen Zahlen entstehen, wenn man zu den rationalen Zahlen ${\displaystyle \mathbb {Q} }$ zusätzliche Lösungen von Gleichungen zulässt? Dieses Konzept führt zum Begriff des Zahlkörpers. Besonders wichtig sind die sogenannten abelschen Erweiterungen – das sind diejenigen Erweiterungen, deren Galoisgruppe kommutativ ist. Der berühmte Satz von Kronecker-Weber beantwortet diese Frage vollständig: Jede abelsche Erweiterung von ${\displaystyle \mathbb {Q} }$ liegt in einem sogenannten zyklotomischen Körper, also einem Körper der Form ${\displaystyle \mathbb {Q} (\zeta _{n})}$, wobei ${\displaystyle \zeta _{n}=e^{\frac {2\pi i}{n}}}$ eine primitive ${\displaystyle n}$-te Einheitswurzel ist.^[74]

Der Schlüssel für die „Parametrisierung“ all dieser Körper ist die natürliche Exponentialfunktion. Setzt man ${\displaystyle e(x):=e^{2\pi ix}}$, so werden durch die Werte ${\displaystyle e(x)}$ an rationalen Stellen ${\displaystyle x\in \mathbb {Q} }$ die Einheitswurzeln erzeugt, also die Eckpunkte des Einheitskreises, die regelmäßig verteilt sind. Diese Zahlen genügen einfachen Polynomgleichungen mit ganzzahligen Koeffizienten (es ist ${\displaystyle e({\tfrac {m}{n}})}$ Nullstelle von ${\displaystyle z^{n}-1}$) und erzeugen genau jene Erweiterungen von ${\displaystyle \mathbb {Q} }$, die in der Kronecker–Weber-Theorie beschrieben werden. Die Exponentialfunktion wirkt hier wie eine „Brücke“: Sie verwandelt rationale Vielfache des Vollwinkels ${\displaystyle 2\pi }$ in algebraische Zahlen, die die gesamte Klasse der abelschen Erweiterungen von ${\displaystyle \mathbb {Q} }$ hervorbringen.^[75]

Die Motivation für weitergehende Vermutungen – wie Kroneckers Jugendtraum^[76] – ist, ob sich ähnliche Beschreibungen auch für andere Zahlkörper gewinnen lassen. Für ${\displaystyle \mathbb {Q} }$ genügt die Exponentialfunktion und die daraus entstehenden Einheitswurzeln (sie „erfüllt“^[76] Kroneckers Jugendtraum im Spezialfall ${\displaystyle K=\mathbb {Q} }$). Für imaginär-quadratische Zahlkörper treten dagegen elliptische Funktionen und die j-Invariante an die Stelle der Exponentialfunktion. Damit wird der Übergang von der klassischen Exponentialarithmetik hin zur komplexen Multiplikation und der Theorie der Modulformen vorbereitet.

Für die Klassifikation abelscher Erweiterungen imaginär-quadratischer Zahlkörper ist das Konzept des Heegner-Punktes zentral. Wechselt man nun von ${\displaystyle \mathbb {Q} }$ zu einem imaginär-quadratischen Zahlkörper ${\displaystyle K=\mathbb {Q} ({\sqrt {d}})}$, dann treten an die Stelle der Einheitswurzeln die sogenannten Heegner-Punkte: Das sind spezielle Punkte ${\displaystyle \tau }$ in der oberen Halbebene ${\displaystyle \mathbb {H} }$, die genau imaginär-quadratische Gitter (also elliptische Kurven mit komplexer Multiplikation) repräsentieren. Setzt man diese Punkte in die ${\displaystyle j}$-Funktion ein, so erhält man algebraische Zahlen ${\displaystyle j(\tau )}$, die gerade die abelschen Erweiterungen von ${\displaystyle K}$ „parametrisieren“. So wie die rationalen Brüche über die Exponentialfunktion zu den Einheitswurzeln führen, die abelsche Erweiterungen von ${\displaystyle \mathbb {Q} }$ erzeugen (Kronecker-Weber), so führen die Heegner-Punkte über die ${\displaystyle j}$-Funktion zu den „Einheitswurzeln der zweiten Art“, die die abelschen Erweiterungen eines imaginär-quadratischen Körpers erzeugen.

Heegner-Punkte ${\displaystyle \tau }$ auf der oberen Halbebene ${\displaystyle \mathbb {H} }$ können dabei nach Bryan Birch wie folgt definiert werden.^[77]

1. Der Wert ${\displaystyle \tau }$ ist ein CM-Punkt (CM = complex multiplication), d. h., er ist Lösung einer quadratischen Gleichung der Form ${\displaystyle A\tau ^{2}+B\tau +C=0}$ mit ganzen Zahlen ${\displaystyle A,B,C}$, für die ${\displaystyle B^{2}-4AC<0}$ gilt.
2. Haben ${\displaystyle A,B,C}$ den größten gemeinsamen Teiler 1, so definiert ${\displaystyle (A,B,C):=Ax^{2}+Bxy+Cy^{2}}$ eine binäre quadratische Form. Gilt außerdem ${\displaystyle A>0}$, so ist die Form positiv definit. Für ${\displaystyle \tau }$ ist ${\displaystyle (A,B,C)}$ dadurch dann eindeutig bestimmt und man nennt ${\displaystyle D(\tau ):=B^{2}-4AC}$ die (ganzzahlige) Diskriminante von ${\displaystyle \tau }$.
3. ${\displaystyle \tau }$ heißt nun Heegner-Punkt mit Level ${\displaystyle N}$ (mit einer natürlichen Zahl ${\displaystyle N}$), falls ${\displaystyle D(N\tau )=D(\tau )}$.

Es gibt zahlreiche Verbindungen zwischen Heegner-Punkten und Modulformen. So nimmt die j-Invariante an Heegner-Punkten stets algebraische Werte an. Hintergrund dieser Aussage ist, dass es für jede natürliche Zahl ${\displaystyle m}$ ein (bis auf Vorzeichen symmetrisches) Polynom ${\displaystyle \Psi _{m}(X,Y)\in \mathbb {Z} [X,Y]}$ vom Grade ${\displaystyle \sigma _{1}(m)}$ gibt, wobei ${\displaystyle \sigma _{1}}$ die klassische Teilerfunktion bezeichnet, sodass ${\displaystyle \Psi _{m}(j(Mz),j(z))\equiv 0}$ (also in ${\displaystyle z}$ die konstante Nullfunktion) für jede ganzzahlige Matrix ${\displaystyle M}$ mit Determinante ${\displaystyle m}$ ist. Der Grad wird über die Konstruktionstechnik

${\displaystyle \prod _{M\in \mathrm {SL} _{2}(\mathbb {Z} )\backslash {\mathfrak {M}}_{m}}(X-j(Mz))=\Psi _{m}(X,j(z))}$

klarer, wobei ${\displaystyle {\mathfrak {M}}_{m}}$ die Menge aller ganzzahligen Matrizen mit Determinante ${\displaystyle m}$ bezeichnet, auf der ${\displaystyle \mathrm {SL} _{2}(\mathbb {Z} )}$ von links operiert und im Quotienten genau ${\displaystyle \sigma _{1}(m)}$ Klassen bildet.^[78] Die Gültigkeit einer solchen Identität kann über die Tatsache gezeigt werden, dass die Koeffizienten der linken Seite in ${\displaystyle \mathbb {H} }$ holomorphe Modulfunktionen (und daher bereits Polynome in ${\displaystyle j}$) sind. Wegen der Fourier-Entwicklung von ${\displaystyle j(z)}$ sind die Koeffizienten von ${\displaystyle \Psi _{m}(X,Y)}$ zudem als rationale Zahlen wählbar. Jeder Heegner-Punkt ${\displaystyle \tau }$ wird von einer Matrix ${\displaystyle M=\left({\begin{smallmatrix}0&-C\\A&B\end{smallmatrix}}\right)}$ mit ganzzahliger Determinante ${\displaystyle \textstyle m=AC={\frac {B^{2}-D}{4}}}$ fixiert. Damit folgt bereits ${\displaystyle \Psi _{m}(j(\tau ),j(\tau ))=0}$ und damit ist ${\displaystyle j(\tau )}$ Nullstelle eines nicht-trivialen Polynoms mit rationalen Koeffizienten. Also ist ${\displaystyle j(\tau )}$ algebraisch – das Argument gilt auch, falls ${\displaystyle (X-Y)|\Psi _{m}(X,Y)}$, da die Funktionen ${\displaystyle j(z)}$ und ${\displaystyle j(Mz)}$ niemals identisch sind.^[79] Diese Werte ${\displaystyle j(\tau )}$ werden traditionell auch als singuläre Moduli (englisch singular moduli) bezeichnet.^[80]

Die algebraischen Eigenschaften der j-Werte an Heegner-Punkten können weiter präzisiert werden über Einführung des sog. Klassenpolynoms (class polynomial)

${\displaystyle H_{D}(X)=\prod _{{\mathfrak {z}}\in \mathrm {SL} _{2}(\mathbb {Z} )\backslash {\mathfrak {Z}}_{D}}(X-j({\mathfrak {z}})).}$

Dabei besteht ${\displaystyle {\mathfrak {Z}}_{D}}$ aus allen Heegner-Punkten mit Führer 1 und Diskriminante ${\displaystyle D}$, auf denen die Gruppe ${\displaystyle \mathrm {SL} _{2}(\mathbb {Z} )}$ operiert. Übrig bleibt ein Polynom ${\displaystyle H_{D}(X)}$ vom Grade ${\displaystyle h(D)}$. Es kann gezeigt werden, dass sogar ${\displaystyle H_{D}(X)\in \mathbb {Z} [X]}$ und stets irreduzibel ist. Im Jahr 1952 konnte Kurt Heegner durch Anwendung vornehmlich Weberscher Modulfunktionen sämtliche imaginärquadratischen Zahlkörper mit Klassenzahl 1 klassifizieren, also solche, in deren Ganzheitsring eine eindeutige Primfaktorzerlegung existiert. Es gibt genau 9 solche imaginärquadratische Zahlkörper, nämlich

${\displaystyle \mathbb {Q} ({\sqrt {-1}}),\mathbb {Q} ({\sqrt {-2}}),\mathbb {Q} ({\sqrt {-3}}),\mathbb {Q} ({\sqrt {-7}}),\mathbb {Q} ({\sqrt {-11}}),\mathbb {Q} ({\sqrt {-19}}),\mathbb {Q} ({\sqrt {-43}}),\mathbb {Q} ({\sqrt {-67}})}$ und ${\displaystyle \mathbb {Q} ({\sqrt {-163}})}$,

womit Heegner eine Vermutung von Carl Friedrich Gauß bestätigte. Damit nimmt insbesondere ${\displaystyle j(\tau )}$ an der Stelle ${\displaystyle \textstyle \tau ={\frac {1+i{\sqrt {163}}}{2}}}$ einen ganzzahligen Wert an, nämlich ${\displaystyle j(\tau )=-640\,320^{3}}$, da ${\displaystyle h(-163)=1}$ und es daher nur eine Klasse von Heegner-Punkten zu dieser Diskriminante gibt. Daraus entsteht die mit einem Computer leicht zu zeigende Kuriositäten^[81]

${\displaystyle e^{\pi {\sqrt {163}}}=262\,537\,412\,640\,768\,743{,}\,999\,999\,999\,999\,250\ldots ,}$

bzw.^[82]

${\displaystyle {\sqrt[{3}]{e^{\pi {\sqrt {163}}}-744}}=640319{,}999\,999\,999\,999\,999\,999\,999\,999\,390\,3173\ldots .}$

Weitere Werte sind:^[83]

${\displaystyle {\begin{array}{rcl}d&\tau &j(\tau )\\\hline -3&{\tfrac {1+i{\sqrt {3}}}{2}}&0\\[0.5em]-4&i&1728\\[0.5em]-7&{\tfrac {1+i{\sqrt {7}}}{2}}&-3375\;=\;-3^{3}\cdot 5^{3}\\[0.5em]-8&i{\sqrt {2}}&8000\;=\;2^{6}\cdot 5^{3}\\[0.5em]-11&{\tfrac {1+i{\sqrt {11}}}{2}}&-32768\;=\;-2^{15}\\[0.5em]-19&{\tfrac {1+i{\sqrt {19}}}{2}}&-884736\;=\;-2^{12}\cdot 3^{3}\cdot 7^{2}\\[0.5em]-43&{\tfrac {1+i{\sqrt {43}}}{2}}&-884736000\;=\;-2^{15}\cdot 3^{3}\cdot 5^{3}\cdot 17^{3}\\[0.5em]-67&{\tfrac {1+i{\sqrt {67}}}{2}}&-147197952000\;=\;-2^{15}\cdot 3^{3}\cdot 5^{3}\cdot 11^{3}\cdot 19^{3}\\[0.5em]-163&{\tfrac {1+i{\sqrt {163}}}{2}}&-262537412640768000\;=\;-2^{18}\cdot 3^{3}\cdot 5^{3}\cdot 23^{3}\cdot 29^{3}\end{array}}}$

Die Identität ${\displaystyle j({\tfrac {1+i{\sqrt {163}}}{2}})=-640\,320^{3}}$ kann dazu verwendet werden, die äußerst schnell konvergierende Reihe

${\displaystyle {\frac {1}{\pi }}={\frac {12}{640\,320^{3/2}}}\sum _{k=0}^{\infty }{\frac {(6k)!(163\cdot 3\,344\,418k+13\,591\,409)}{(3k)!(k!)^{3}(-640\,320)^{3k}}}}$

herzuleiten,^[84] vergleiche auch Chudnovsky-Algorithmus. Mit diesem ist eine sehr schnelle Berechnung von ${\displaystyle \pi }$ möglich: Bis heute (Stand August 2025) sind mit dieser Methode 300 Billionen Stellen nach dem Komma berechnet worden.^[85]

Mit Hilfe einer Formel von Sarvadaman Chowla und Atle Selberg können singuläre Moduli auch auf den Fall von Modulformen mit algebraischen Koeffizienten „übertragen“ werden. Die Aussage ist, dass, falls ${\displaystyle K}$ ein imaginär-quadratischer Zahlkörper ist, eine nur von diesem Körper abhängige „Periode“ ${\displaystyle \Omega _{K}}$ existiert, sodass für jede Modulform ${\displaystyle f}$ mit algebraischen Koeffizienten ${\displaystyle f(\tau )\in {\overline {\mathbb {Q} }}\cdot \Omega _{K}^{k}}$ für alle ${\displaystyle \tau \in \mathbb {H} \cap K}$ gilt. Ein möglicher Wert von ${\displaystyle \Omega _{K}}$ kann explizit berechnet werden als

${\displaystyle \Omega _{K}={\frac {1}{\sqrt {2\pi |D|}}}\prod _{j=1}^{|D|-1}\Gamma \left({\frac {j}{|D|}}\right)^{\frac {\chi _{D}(j)w(D)}{4h(D)}},}$

wobei ${\displaystyle \chi _{D}}$ der Charakter bezüglich der Diskriminante ${\displaystyle D}$ des Zahlkörpers ${\displaystyle K}$, ${\displaystyle h(D)}$ die Klassenzahl, ${\displaystyle w(D)}$ die Anzahl der Einheiten im Ganzheitsring ${\displaystyle {\mathcal {O}}_{K}}$^[81] und ${\displaystyle \Gamma (s)}$ die Gammafunktion bezeichnet.^[86] Diese Formel wurde 1949 von Chowla und Selberg publiziert, war aber bereits 1897 von Matyáš Lerch entdeckt worden.^[86][87]

Im Jahr 1974 bewies Pierre Deligne die Weil-Vermutungen vollständig. Diese treffen eine Aussage über die Lösungsanzahlen von Varietäten über endlichen Körpern, mit zahlreichen Anwendungen in der Mathematik. Der Beweis umfasste ebenfalls die besonders schwierige lokale Riemannsche Vermutung und gehört zu den größten mathematischen Durchbrüchen des 20. Jahrhunderts. Eine direkte Konsequenz ist die Ramanujan-Vermutung, die eine scharfe obere Grenze für die Fourier-Koeffizienten von Spitzenformen (Modulformen mit bestimmten Eigenschaften), liefert. Deligne erhielt für diese Leistungen 1978 die Fields-Medaille.

Es ist durch wegweisende Arbeiten von Jacob Bekenstein und Stephen Hawking in den 1970er Jahren bekannt, dass schwarze Löcher eine thermodynamische Entropie besitzen und daher aus einer Sammlung mikroskopischer Quantenzustände bestehen sollten (siehe auch Bekenstein-Hawking-Entropie). Im Rahmen der Superstringtheorie können gewisse Anzahlen mikroskopischer Zustände in Verbindung gebracht werden, die das quantenstatistische System eines schwarzen Lochs bilden – was ihr thermodynamisches Verhalten aus einer fundamentaleren Perspektive erklärt. Der grundlegende Zusammenhang zu Modulformen ergibt sich aus der Beobachtung, dass in der einfachsten superstring-theoretischen Konstruktion die erzeugende Funktion der Anzahl der mikroskopischen Zustände eine Modulform ist. In einer Richtung fungiert die modulare Symmetrie als mächtiger Leitfaden für die Berechnung von quantengravitativen Effekten auf die Entropie des schwarzen Lochs. In der anderen Richtung hat dieser Zusammenhang zur Entdeckung überraschender Beziehungen zwischen den „Mock-Modulformen“ – erste Beispiele wurden von Srinivasa Ramanujan bereits in der 1910ern konstruiert – und einer Klasse stringtheoretischer schwarzer Löcher geführt, was eine unendliche Anzahl neuer Beispiele für Mock-Modulformen liefert.

Richard Borcherds zeigte 1992 mit der Hilfe sog. Vertex-Algebren im Rahmen des Monstrous moonshine (gelegentlich auch Moonshine theory, dt.: „Mondscheintheorie“), dass es einen überraschenden Zusammenhang zwischen den Fourier-Koeffizienten der j-Funktion – einer Modulfunktion – und der Monstergruppe gibt. Die Monstergruppe ist mit ca. ${\displaystyle 8\times 10^{53}}$ Elementen die größte unter den 26 sporadischen Gruppen, die sich im Rahmen der Klassifikation aller endlichen einfachen Gruppen in keine der dort gegebenen Klassen (mit je unendlich vielen Vertretern) einordnen lassen. Die Monstergruppe kann zum Beispiel als Automorphismengruppe einer kommutativen, nicht-assoziativen Algebra auf einem 196883-dimensionalen Raum realisiert werden – und zum Beispiel ist 196884 genau der erste Fourier-Koeffizient der j-Funktion. Borcherds erhielt für diese Leistung 1998 die Fields-Medaille.

Um zu verstehen, was elliptische Kurven mit Modulformen zu tun haben, ist es hilfreich, sich zunächst das Beispiel quadratischer Gleichungen anzusehen. Fred Diamond und Jerry Shurman weisen darauf hin, dass das quadratische Reziprozitätsgesetz dazu verwendet werden kann, die Anzahlen der Lösungen modulo ${\displaystyle p}$ der Gleichung

${\displaystyle Q\colon \quad x^{2}=d\qquad (d\in \mathbb {Z} \setminus \{0\})}$

als sog. Eigenwerte von linearen Abbildungen

${\displaystyle T_{p}\colon V_{Q}\to V_{Q}}$

zwischen einem zur Gleichung ${\displaystyle Q}$ gehörigen ${\displaystyle \mathbb {C} }$-Vektorraum ${\displaystyle V_{Q}}$ zu interpretieren. Zunächst hat ${\displaystyle Q}$ über ${\displaystyle \mathbb {F} _{p}}$ die Diskriminante ${\displaystyle D_{Q}=4d}$, und die Gleichung insgesamt ${\displaystyle a_{p}(Q)+1}$ Lösungen, wenn

${\displaystyle a_{p}(Q):=\left({\frac {4d}{p}}\right).}$

Wie im Abschnitt zur Verteilung quadratischer Reste gesehen, hängt die Größe ${\displaystyle a_{p}(Q)}$ wegen des quadratischen Reziprozitätsgesetzes ausschließlich von der Restklasse ${\displaystyle {\overline {p}}}$ modulo ${\displaystyle 4|d|}$ ab. Der Schlüssel ist nun, über die eindeutige Primfaktorzerlegung die ${\displaystyle a_{p}(Q)}$ auf beliebige natürliche Argumente ${\displaystyle n=p_{1}^{c_{1}}p_{2}^{c_{2}}\cdots p_{r}^{c_{r}}}$ fortzusetzen mittels der Regel

${\displaystyle a_{n}(Q):=a_{p_{1}}(Q)^{c_{1}}\cdot a_{p_{2}}(Q)^{c_{2}}\cdots a_{p_{r}}(Q)^{c_{r}}.}$

Damit sind die ${\displaystyle a_{n}(Q)}$ vollständig multiplikativ, also gilt stets ${\displaystyle a_{mn}(Q)=a_{m}(Q)a_{n}(Q)}$. Als Vektorraum ${\displaystyle V_{Q}}$ kann man nun die Kollektion aller Abbildungen von der Gruppe der primen Restklassen modulo ${\displaystyle 4|d|}$ in die komplexen Zahlen definieren, also

${\displaystyle V_{Q}:=\{f\colon (\mathbb {Z} /4|d|\mathbb {Z} )^{\times }\to \mathbb {C} \}.}$

Da die Gruppe ${\displaystyle (\mathbb {Z} /4|d|\mathbb {Z} )^{\times }}$ endlich ist, ist ${\displaystyle V_{Q}}$ endlichdimensional. Auf ${\displaystyle V_{Q}}$ kann nun ein System von linearen Abbildungen ${\displaystyle T_{p}}$ (mit ${\displaystyle p}$ Primzahl) betrachtet werden:

${\displaystyle (T_{p}f)({\overline {n}}):={\begin{cases}f({\overline {pn}}),&\qquad 4|d|\not \equiv 0{\pmod {p}},\\0,&\qquad {\text{sonst}}.\end{cases}}}$

Dabei verstehen sich die Reduktionen ${\displaystyle {\overline {n}}}$ und ${\displaystyle {\overline {pn}}}$ modulo ${\displaystyle 4|d|}$. Da man die ${\displaystyle a_{p}(Q)}$ als simultane Eigenwerte begreifen will, muss nun noch eine geeignete Funktion ${\displaystyle f_{Q}\in V_{Q}}$ gefunden werden. Nach dem quadratischen Reziprozitätsgesetz ist die Wahl ${\displaystyle f_{Q}({\overline {n}}):=a_{n}(Q)}$ wohldefiniert. Mit der Multiplikativität der ${\displaystyle a_{n}(Q)}$ folgt^[89]

${\displaystyle (T_{p}f_{Q})(n)=a_{pn}(Q)=a_{p}(Q)a_{n}(Q)=a_{p}(Q)f_{Q}(n),\quad }$ also ${\displaystyle \quad T_{p}f_{Q}=a_{p}(Q)f_{Q}.}$

Also ist ${\displaystyle f_{Q}\in V_{Q}}$ ein Eigenvektor von ${\displaystyle T_{p}}$ mit Eigenwert ${\displaystyle a_{p}(Q)}$.

Im Jahr 1995 konnten Andrew Wiles und Richard Taylor im Rahmen des Modularitätssatzes zeigen, dass alle semi-stabilen elliptischen Kurven modular sind, also von einer Modulform „abstammen“. Dahinter verbirgt sich eine Parametrisierung elliptischer Kurven durch Modulformen, ähnlich wie zum Beispiel Sinus und Kosinus den Einheitskreis parametrisieren. Jedoch geht die Aussage des Satzes viel tiefer und impliziert eine „zahlentheoretische Beziehung“ zwischen elliptischen Kurven und Modulformen. Eine Konsequenz des Modularitätssatzes ist der Große Satz von Fermat und sein Beweis wird als einer der Höhepunkte der Mathematik des 20. Jahrhunderts gesehen. Im Umfeld der bis heute ungelösten Vermutung von Birch und Swinnerton-Dyer, einem Millennium-Problem der Mathematik, werden zudem Zusammenhänge zwischen der Anzahl rationaler Punkte auf elliptischen Kurven und den „analytischen Eigenschaften“ ihrer Modulformen (bzw. deren L-Funktionen), vermutet.

Im Jahr 2016 löste Maryna Viazovska mit Hilfe der Theorie der Modulformen das Problem der dichtester Kugelpackungen in 8 Dimensionen. Dies gilt als einer der größten Durchbrüche der diskreten Mathematik der letzten Jahrzehnte. Viazovska erhielt für diese Leistung im Jahr 2022 die Fields-Medaille.

Die Modulformen vom Gewicht ${\displaystyle k}$ bilden einen ${\displaystyle \mathbb {C} }$-Vektorraum (also ein Vektorraum über den komplexen Zahlen), ebenso die ganzen Modulformen und auch die Spitzenformen. Es sind folgende Notationen gebräuchlich:

• ${\displaystyle {\mathcal {V}}_{k}}$ ist der Vektorraum der (meromorphen) Modulformen vom Gewicht ${\displaystyle k}$ zur vollen Modulgruppe,^[90]
• ${\displaystyle {\mathcal {M}}_{k}}$ ist der Vektorraum der ganzen Modulformen vom Gewicht ${\displaystyle k}$ zur vollen Modulgruppe,^[91]
• ${\displaystyle {\mathcal {S}}_{k}}$ ist der Vektorraum der Spitzenformen vom Gewicht ${\displaystyle k}$ zur vollen Modulgruppe,
• ${\displaystyle {\mathcal {M}}_{k}^{!}}$ ist der Vektorraum der schwach holomorphen Modulformen vom Gewicht ${\displaystyle k}$ zur vollen Modulgruppe, d. h., es sind Polstellen in ${\displaystyle z=i\infty }$ zugelassen.

Offenbar gilt:

${\displaystyle {\mathcal {S}}_{k}\subset {\mathcal {M}}_{k}\subset {\mathcal {M}}_{k}^{!}\subset {\mathcal {V}}_{k}.}$

Das Produkt zweier Modulformen der Gewichte ${\displaystyle k_{1}}$ und ${\displaystyle k_{2}}$ ist eine Modulform des Gewichts ${\displaystyle k_{1}+k_{2}}$, also gilt ${\displaystyle {\mathcal {V}}_{k_{1}}{\mathcal {V}}_{k_{2}}\subseteq {\mathcal {V}}_{k_{1}+k_{2}}}$.^[90] Selbiges gilt für Spitzenformen und schwach holomorphe Modulformen. Demnach hat man

${\displaystyle \bigoplus _{k\in \mathbb {Z} }{\mathcal {S}}_{k}\subset \bigoplus _{k\in \mathbb {Z} }{\mathcal {M}}_{k}\subset \bigoplus _{k\in \mathbb {Z} }{\mathcal {M}}_{k}^{!}\subset \bigoplus _{k\in \mathbb {Z} }{\mathcal {V}}_{k}}$

als aufsteigende Kette graduierter Algebren. Dabei bezeichnet ${\displaystyle \bigoplus }$ die direkte Summe. Die Spitzenformen ${\displaystyle \bigoplus _{k\in \mathbb {Z} }{\mathcal {S}}_{k}}$ können ferner als ein Ideal^[92] im Ring ${\displaystyle \bigoplus _{k\in \mathbb {Z} }{\mathcal {M}}_{k}}$ aufgefasst werden, denn sie bilden den Kern des Ringhomomorphismus

${\displaystyle \bigoplus _{k\in \mathbb {Z} }{\mathcal {M}}_{k}\longrightarrow \bigoplus _{k\in \mathbb {Z} }\mathbb {C} }$

der komponentenweise ${\displaystyle f\mapsto a_{0}(f)}$ vollzieht, also jede Modulform auf ihren nullten Fourier-Koeffizieten sendet.

Im Folgenden ist ${\displaystyle k}$ eine gerade, ganze Zahl. Wegen ihrer starken Transformationseigenschaften kombiniert mit der Theorie meromorpher Funktionen können restriktive Eigenschaften an die Null- und Polstellen von Modulformen ${\displaystyle 0\not =f\in {\mathcal {V}}_{k}}$ gestellt werden. Unter Anwendung des Residuensatzes^[93] ergibt sich die berühmte Valenzformel,^[94] manchmal auch ${\displaystyle {\tfrac {k}{12}}}$-Formel^[95] oder Gewichtsformel^[96] genannt:

${\displaystyle {\frac {1}{2}}\mathrm {ord} _{i}(f)+{\frac {1}{3}}\mathrm {ord} _{\rho }(f)+\mathrm {ord} _{i\infty }(f)+\sum _{\tau \in \mathrm {SL} _{2}(\mathbb {Z} )\backslash \mathbb {H} \atop \tau \not =[i],[\rho ]}\mathrm {ord} _{\tau }(f)={\frac {k}{12}}.}$

Hierbei ist ${\displaystyle \rho :=e^{\frac {2\pi i}{3}}}$ und es steht ${\displaystyle \mathrm {ord} _{z_{0}}(f)}$ für die Ordnung der Funktion ${\displaystyle f}$ im Punkt ${\displaystyle z=z_{0}}$. Im Falle ${\displaystyle z=i\infty }$ kann man diese direkt an der Fourier-Entwicklung ablesen – der Index des ersten nicht-verschwindenden Koeffizienten definiert die Ordnung.^[97] An Nullstellen ist diese positiv (und entspricht der Vielfachheit der Nullstelle), an Polstellen ist sie entsprechend negativ. Sie kann als ein Analogon zu den Liouvilleschen Sätzen aus der Theorie der elliptischen Funktionen gesehen werden.^[98] Interpretiert man Modulformen des Gewichts ${\displaystyle 2k}$ ferner als sog. meromorphe k-Formen auf der Moddulkurve ${\displaystyle X(1)}$, ist ein Beweis der Valenzformel auch über den Satz von Riemann-Roch möglich.^[99]

Die Valenzformel hat weitreichende Konsequenzen – im Besonderen für die Theorie ganzer Modulformen. In diesem Spezialfall sind alle Ordnungen nicht-negativ, da nirgends Polstellen vorliegen. Eine direkte Konsequenz ist, dass es keine nichttrivialen ganzen Modulformen zum Gewicht ${\displaystyle k=2}$ und Gewichten ${\displaystyle k<0}$ zur vollen Modulgruppe geben kann, da es in etwa bei ${\displaystyle k=2}$ keine Kombination schafft, auf den Wert ${\displaystyle {\tfrac {1}{6}}}$ auf der rechten Seite zu kommen. Allgemein lassen sich mit der Valenzformel Dimensionsformeln für die ${\displaystyle {\mathcal {M}}_{k}}$ bzw. ${\displaystyle {\mathcal {S}}_{k}}$ ableiten.

Es gilt für gerade ${\displaystyle k\geq 0}$:^[100]

${\displaystyle \mathrm {dim} \,{\mathcal {M}}_{k}={\begin{cases}\left[{\frac {k}{12}}\right],&{\mbox{falls}}\;k\equiv 2\;(\mathrm {mod} \ 12)\\\left[{\frac {k}{12}}\right]+1,&{\mbox{falls}}\;k\not \equiv 2\;(\mathrm {mod} \ 12)\end{cases}}}$

${\displaystyle \mathrm {dim} \,{\mathcal {S}}_{k}={\begin{cases}\left[{\frac {k}{12}}\right]-1,&{\mbox{falls}}\;k\equiv 2\;(\mathrm {mod} \ 12),k\geq 12\\\left[{\frac {k}{12}}\right],&{\mbox{falls}}\;k\not \equiv 2\;(\mathrm {mod} \ 12),k\geq 12\\0,&{\mbox{falls}}\;k<12.\end{cases}}}$

Dabei steht ${\displaystyle [x]}$ für die größte ganze Zahl, sodass ${\displaystyle [x]\leq x}$. Die Tatsache, dass dies endlichdimensionale Vektorräume sind, ist einer der wesentlichen Gründe, weshalb die Theorie der (ganzen) Modulformen so bedeutend für die Zahlentheorie ist. Ein Grund für die Nützlichkeit von Modulformen in unterschiedlichsten Anwendung ist dabei insbesondere, dass sie zwar häufig unterschiedliche Beschreibungen in den verschiedensten Anwendungen haben, man aber sofort Verbindungen unter den Modulformen findet, da die Vektorräume von relativ kleiner Dimension sind.^[101]

Da durch die Multiplikation mit der Spitzenform ${\displaystyle \Delta }$ (Diskriminante) vom Gewicht 12 ein Isomorphismus von ${\displaystyle {\mathcal {M}}_{k-12}}$ nach ${\displaystyle {\mathcal {S}}_{k}}$ gegeben ist, gilt^[102]

${\displaystyle \mathrm {dim} \,{\mathcal {S}}_{k}=\mathrm {dim} \,{\mathcal {M}}_{k-12},\quad \mathrm {falls} \quad k\geq 12.}$

Die Vektorräume ${\displaystyle {\mathcal {M}}_{k}}$ für ${\displaystyle k=0,4,6,8,10,14}$ sind eindimensional und werden erzeugt von den ${\displaystyle 1,E_{4},E_{6},E_{4}^{2},E_{4}\cdot E_{6},E_{4}^{2}\cdot E_{6}}$ und für ${\displaystyle k=12}$ zweidimensional, erzeugt von ${\displaystyle E_{4}^{3}}$ und ${\displaystyle E_{6}^{2})}$ mit den Eisensteinreihen ${\displaystyle E_{4},E_{6}}$.^[103] Allgemein kann man zeigen, dass alle Elemente von ${\displaystyle {\mathcal {M}}_{k}}$ durch Polynome in ${\displaystyle E_{4},E_{6}}$ erzeugt werden, und dies sogar eindeutig:^[104]

${\displaystyle {\mathcal {M}}_{k}=\bigoplus _{a,b\in \mathbb {N} _{0} \atop 4a+6b=k}\mathbb {C} E_{4}^{a}E_{6}^{b}.}$

Es ist aber häufig nützlicher, Basen von Eigenformen der Hecke-Operatoren zu verwenden (Atkin-Lehner-Theorie).

Man kann mit dem Satz von Riemann-Roch Aussagen über die Dimension der Vektorräume der ganzen Modulformen und Spitzenformen zu Kongruenzuntergruppen machen.

Ist ${\displaystyle f\in {\mathcal {M}}_{k}}$ mit ${\displaystyle k\geq 0}$, so gilt^[105]

${\displaystyle f(x+iy)\ll y^{-k}}$

gleichmäßig in ${\displaystyle x\in \mathbb {R} }$, wenn ${\displaystyle y\to 0^{+}}$. Für Spitzenformen kann dies verbessert werden. Ist sogar ${\displaystyle f\in {\mathcal {S}}_{k}}$, so gilt

${\displaystyle f(x+iy)\ll y^{-{\frac {k}{2}}}}$

gleichmäßig in ${\displaystyle x\in \mathbb {R} }$, wenn ${\displaystyle y\to 0^{+}}$. Wichtig ist, dass selbst nichttriviale Spitzenformen keinesfalls beschränkt sind mit zunehmender Nähe von ${\displaystyle \mathbb {R} }$, da ihr Verschwinden nur in Umgebungen rationaler Zahlen (in der Topologie auf ${\displaystyle \mathbb {H} ^{*}}$) „bemerkbar“ wird.

Für die volle Modulgruppe ${\displaystyle \mathrm {SL} _{2}(\mathbb {Z} )}$ lassen sich auf dem Vektorraum der Modulformen vom Gewicht ${\displaystyle k}$ die sogenannten Hecke-Operatoren definieren, benannt nach Erich Hecke. Diese Operatoren liefern eine Familie von kommutierenden, bezgl. des Petersson-Skalarproduktes (siehe unten) selbstadjungierten Endomorphismen mit tiefer arithmetischer Bedeutung.

Die Hecke-Theorie liefert eine kanonische Basis von Eigenformen mit arithmetisch bedeutenden Fourier-Koeffizienten. Ihre Koeffizienten sind multiplikativ und erfüllen gewisse Rekursionen. Damit schlägt die Theorie eine Brücke zwischen Modulformen, L-Funktionen und Galois-Darstellungen. Sie bildet zudem den Ausgangspunkt für die moderne Modultheorie in der Zahlentheorie, einschließlich des Langlands-Programms und des Beweises des großen Fermatschen Satzes.

Für ${\displaystyle \textstyle f(z)=\sum _{n=0}^{\infty }a_{n}(f)q^{n}}$ eine ganze Modulform vom Gewicht ${\displaystyle k}$ und für eine natürliche Zahl ${\displaystyle n}$ ist der Hecke-Operator ${\displaystyle T_{n}\colon {\mathcal {M}}_{k}\to {\mathcal {M}}_{k}}$ durch^[106]

${\displaystyle (T_{n}f)(z):={\frac {1}{n}}\sum _{ad=n \atop 0\leq b<d}a^{k}\,f\!\left({\frac {az+b}{d}}\right)}$

definiert. Er schickt Spitzenformen auf Spitzenformen, kann also zu einem Endomorphismus ${\displaystyle {\mathcal {S}}_{k}\to {\mathcal {S}}_{k}}$ eingeschränkt werden.^[107] Zu beachten ist, dass ${\displaystyle T_{n}}$ auch vom Gewicht ${\displaystyle k}$ abhängt, diese Abhängigkeit aber oft nicht angezeigt wird, da sie sich meist aus dem Kontext ergibt.

In der Darstellung mittels Fourier-Reihen wirkt ${\displaystyle T_{n}}$ auf die Koeffizienten durch^[108]

${\displaystyle (T_{n}f)(z)=\sum _{m=0}^{\infty }\left(\sum _{d\mid \mathrm {ggT} (m,n)}d^{k-1}\,a_{\tfrac {mn}{d^{2}}}(f)\right)q^{m}.}$

Die Hecke-Operatoren erfüllen eine Reihe an nützlichen und wichtigen Eigenschaften:

• Die Operatoren ${\displaystyle T_{m}}$ und ${\displaystyle T_{n}}$ kommutieren für alle ${\displaystyle m,n\in \mathbb {N} }$: ${\displaystyle T_{m}T_{n}=T_{n}T_{m}}$.^[108]
• Es gilt die Multiplikativitätsrelation^[108]

${\displaystyle T_{m}T_{n}=\sum _{d\mid \mathrm {ggT} (m,n)}d^{\,k-1}\,T_{\tfrac {mn}{d^{2}}}.}$

Insbesondere gilt ${\displaystyle T_{mn}=T_{m}T_{n}}$ für teilerfremde ${\displaystyle m,n}$.

• Für Primzahlen ${\displaystyle p}$ vereinfacht sich dies zu^[109]

${\displaystyle T_{p}T_{p^{r}}=T_{p^{r+1}}+p^{k-1}T_{p^{r-1}}.}$

Eine Modulform ${\displaystyle f}$ heißt Hecke-Eigenform (oder kurz Eigenform), wenn sie simultan Eigenfunktion aller ${\displaystyle T_{n}}$ ist.^[110] Für eine normierte Eigenform (d. h. ${\displaystyle a_{1}(f)=1}$) gilt dann^[111]

${\displaystyle T_{n}f=a_{n}(f)f,}$

wobei ${\displaystyle a_{n}(f)}$ die Fourier-Koeffizienten von ${\displaystyle f}$ sind (siehe oben).

Die Multiplikativitätsrelation der ${\displaystyle T_{n}}$ überträgt sich auf die Koeffizienten:^[110]

• ${\displaystyle a_{mn}(f)=a_{m}(f)a_{n}(f)}$, falls ${\displaystyle \mathrm {ggT} (m,n)=1}$.
• Für Primzahlpotenzen gilt die Rekursion^[110]

${\displaystyle a_{p^{r+1}}(f)=a_{p}(f)a_{p^{r}}(f)-p^{k-1}a_{p^{r-1}}(f).}$

Die Hecke-Eigenwerte ${\displaystyle a_{p}(f)}$ einer normierten Eigenform mit Primzahlen ${\displaystyle p}$ induzieren die Euler-Faktoren der zugehörigen L-Funktion:^[112]

${\displaystyle L(f,s)=\sum _{n=1}^{\infty }{\frac {a_{n}(f)}{n^{s}}}=\prod _{p\,{\text{Primzahl}}}{\frac {1}{1-a_{p}(f)p^{-s}+p^{k-1-2s}}}.}$

Es kann gezeigt werden, dass genau dann eine solche Produktentwicklung vorliegt, wenn ${\displaystyle f}$ eine normierte Hecke-Eigenform ist.^[113]

Diese Euler-Produkte verbinden Modulformen mit der Zahlentheorie (z. B. Darstellung von Primzahlen, Verteilung der ${\displaystyle a_{p}(f)}$, Verknüpfung mit Galois-Darstellungen). Delignes Beweis der Weil-Vermutungen lieferte die scharfe Schranke

${\displaystyle |a_{p}(f)|\leq 2p^{\frac {k-1}{2}}}$

für Eigenformen und Primzahlen ${\displaystyle p}$. Die Verteilung der Werte

${\displaystyle {\frac {a_{p}(f)}{2p^{\frac {k-1}{2}}}}}$

im Intervall ${\displaystyle [-1,1]}$ ist Gegenstand der Sato-Tate-Vermutung.

Für Modulformen zur vollen Modulgruppe spielt das Petersson-Skalarprodukt eine zentrale Rolle. Ist ${\displaystyle f}$ eine Spitzenform vom Gewicht ${\displaystyle k}$ mit Fourier-Entwicklung

${\displaystyle f(z)=\sum _{n=1}^{\infty }a_{n}(f)q^{n}}$ und ebenso ${\displaystyle g(z)=\sum _{n=1}^{\infty }a_{n}(g)q^{n}}$,

so definiert man^[114]

${\displaystyle \langle f,g\rangle :=\int _{\mathrm {SL} _{2}(\mathbb {Z} )\backslash \mathbb {H} }f(z)\,{\overline {g(z)}}\,y^{k}\,{\frac {\mathrm {d} x\,\mathrm {d} y}{y^{2}}},\qquad z=x+iy.}$

Hierbei bedeutet ${\displaystyle {\overline {w}}}$ die komplexe Konjugation. Das Integral läuft über einen Fundamentalbereich der vollen Modulgruppe und konvergiert für Spitzenformen. Hans Petersson führte das Petersson-Skalarprodukt im Raum der Spitzenformen ein und machte diese damit zu einem Hilbertraum. Besonders wichtig ist, dass die Hecke-Operatoren selbstadjungiert bezüglich dieses Skalarprodukts sind, also^[115]

${\displaystyle \langle T_{n}f,g\rangle =\langle f,T_{n}g\rangle .}$

Daraus folgt über elementare lineare Algebra, dass es eine orthogonale Basis von Hecke-Eigenformen gibt.^[116] Eisensteinreihen sind bezüglich des Petersson-Skalarprodukts orthogonal zu den Spitzenformen. Dies kann zum Beispiel mit der Petersson-Koeffizietenformel eingesehen werden, siehe im Abschnitt zu Poincaré-Reihen.^[117]

Die Norm ${\displaystyle ||f||^{2}=\langle f,f\rangle }$ einer Eigenform enthält tiefe arithmetische Informationen. Über Rankins Methode und spezielle Werte von L-Funktionen lassen sich diese Normen explizit berechnen (siehe unten). Damit verbindet das Petersson-Skalarprodukt die analytische Struktur der Modulformenräume mit den arithmetischen Eigenschaften ihrer Fourier-Koeffizienten.

Poincaré-Reihen, benannt nach Henri Poincaré, sind ein grundlegendes Werkzeug zur expliziten Konstruktion von Modulformen. Sie entstehen durch periodisches Fortsetzen einer einfach strukturierten Funktion über die volle Modulgruppe. Gleichzeitig verallgemeinern sie die Eisensteinreihen.

Für gerade, ganze Zahlen ${\displaystyle k\geq 4}$ und ${\displaystyle m\geq 0}$ definiert man die holomorphe Poincaré-Reihe^[118]

${\displaystyle P_{m,k}(z)\;=\;\sum _{\gamma \in \Gamma _{\infty }\backslash \mathrm {SL} _{2}(\mathbb {Z} )}(cz+d)^{-k}\,e^{2\pi im\gamma (z)},}$

wobei ${\displaystyle \gamma ={\begin{pmatrix}a&b\\c&d\end{pmatrix}}}$ und ${\displaystyle \Gamma _{\infty }}$ die Untergruppe der Translationen ${\displaystyle \{\pm {\begin{pmatrix}1&n\\0&1\end{pmatrix}}:n\in \mathbb {Z} \}}$ ist. Der Summand ist so gewählt, dass er invariantes Gewicht ${\displaystyle k}$ hat.

Für ${\displaystyle k>2}$ konvergiert die Reihe absolut und definiert eine Spitzenform vom Gewicht ${\displaystyle k}$. Sie können, wie auch die Eisensteinreihen, auf Kongruenzuntergruppen verallgemeinert werden.^[117]

Es kann gezeigt werden, dass sie für ${\displaystyle m\geq 1}$ Spitzenformen sind und den gesamten Raum ${\displaystyle {\mathcal {S}}_{k}}$ aufspannen.^[117]

Die Poincaré-Reihen besitzen eine explizite Fourier-Entwicklung der Form

${\displaystyle P_{m,k}(z)\;=\;\sum _{n=1}^{\infty }a_{m,k}(n)\,q^{n}.}$

Die Koeffizienten ${\displaystyle a_{m,k}(n)}$ lassen sich durch Kloosterman-Summen und Bessel-Funktionen ausdrücken:

${\displaystyle a_{m,k}(n)\;=\;\left({\frac {n}{m}}\right)^{\frac {k-1}{2}}\left(\delta _{m,n}+2\pi i^{-k}\sum _{c=1}^{\infty }{\frac {1}{c}}\,K(m,n;c)\,J_{k-1}\!\left({\tfrac {4\pi {\sqrt {mn}}}{c}}\right)\right),}$

wobei ${\displaystyle \delta _{m,n}}$ das Kronecker-Delta bezeichnet und

${\displaystyle K(m,n;c)=\sum _{d{\bmod {c}} \atop \mathrm {ggT} (d,c)=1}e^{2\pi i{\tfrac {md+n{\overline {d}}}{c}}}}$ (mit ${\displaystyle d{\overline {d}}\equiv 1{\bmod {c}}}$)

die Kloosterman-Summe und ${\displaystyle J_{k-1}}$ die Bessel-Funktion ist.^[117]

Ein wesentliches Strukturmerkmal ist die Orthogonalität im Petersson-Skalarprodukt. Für jede Spitzenform ${\displaystyle \textstyle f(z)=\sum _{n=1}^{\infty }a_{n}(f)q^{n}}$ gilt^[117]

${\displaystyle \langle f,P_{m,k}\rangle \;=\;{\frac {(k-2)!}{(4\pi m)^{k-1}}}\,a_{m}(f).}$

Damit erlaubt es die Familie der Poincaré-Reihen ${\displaystyle \{P_{m,k}\}_{m\geq 1}}$ die Fourier-Koeffizienten beliebiger Spitzenformen direkt über das Skalarprodukt mit ${\displaystyle P_{m,k}}$ zu rekonstruieren. Auch für ${\displaystyle m=0}$ behält die Koeffizientenformel ihre Gültigkeit, was zeigt, dass Eisensteinreihen orthogonal auf den Spitzenformen stehen.^[117]

Die Atkin–Lehner-Theorie untersucht zusätzliche Symmetrien und Zerlegungen von Räumen von Modulformen. Ursprünglich wurde sie für Kongruenzuntergruppen ${\displaystyle \Gamma _{0}(N)}$ entwickelt, wo es für jeden Teiler ${\displaystyle Q\mid N}$ einen sogenannten Atkin–Lehner-Involution ${\displaystyle W_{Q}}$ gibt, der auf den Raum der Spitzenformen wirkt. Diese Operatoren vertauschen mit den Hecke-Operatoren und sind Involutionen, d. h. es gilt ${\displaystyle W_{Q}^{2}=1}$. Sie erlauben eine Zerlegung der Modulformenräume in Unterräume, die nach dem Vorzeichen des Eigenwerts von ${\displaystyle W_{Q}}$ unterschieden werden.

Für die volle Modulgruppe ${\displaystyle \Gamma =\mathrm {SL} _{2}(\mathbb {Z} )}$ entspricht dies dem Spezialfall ${\displaystyle N=1}$. In diesem Fall existiert nur der triviale Atkin–Lehner-Operator ${\displaystyle W_{1}=\mathrm {Id} }$, sodass keine nichttriviale zusätzliche Zerlegung entsteht. Dennoch ist die Theorie auch hier von Bedeutung, da sie die konzeptionelle Grundlage für die Einbettung der Modulformen zur vollen Modulgruppe in das allgemeinere Bild der Modulformen zu höheren Stufen liefert.

Die zentrale Idee besteht darin, dass die Atkin–Lehner-Involutionen zusammen mit den Hecke-Operatoren eine große kommutative Familie von Operatoren erzeugen, die die Struktur der Modulformenräume vollständig kontrolliert. In den Räumen höherer Stufe lassen sich so Eigenformen eindeutig durch ihre Hecke-Eigenwerte und Atkin–Lehner-Eigenwerte charakterisieren. Für die volle Modulgruppe reduziert sich das Bild auf die Hecke-Theorie allein, doch die Atkin–Lehner-Theorie erklärt, wie diese Situation in den allgemeineren Kontext eingebettet ist.

Die Fourier-Entwicklungen von Modulformen zur vollen Modulgruppe enthalten arithmetisch bedeutende Koeffizienten. Es stellt sich die grundlegende Frage, wie groß diese Koeffizienten asymptotisch werden können. Die Situation unterscheidet sich deutlich zwischen Eisensteinreihen und Spitzenformen.

Für eine Eisensteinreihe

${\displaystyle E_{k}(z)=1-{\frac {2k}{B_{k}}}\sum _{n=1}^{\infty }\sigma _{k-1}(n)\,q^{n}}$

sind die Fourier-Koeffizienten (im Wesentlichen) durch die Teilerfunktionen ${\displaystyle \sigma _{k-1}(n)}$ gegeben. Mit elementaren Mitteln folgt sofort für ${\displaystyle k>2}$^[119]

${\displaystyle n^{k-1}\leq \sum _{d|n}d^{k-1}=\sigma _{k-1}(n)=n^{k-1}\sum _{d|n}{\frac {1}{d^{k-1}}}\leq n^{k-1}\sum _{m=1}^{\infty }{\frac {1}{m^{k-1}}}=\zeta (k-1)n^{k-1}\ll n^{k-1}.}$

Damit erhält man eine aus mathematischer Sicht sehr präzise Kontrolle über die Größenordnung der Koeffizienten der Eisensteinreihen.^[120]

Für Spitzenformen ${\displaystyle f(z)=\textstyle \sum _{n=1}^{\infty }a_{n}(f)q^{n}}$ ist die Lage subtiler. Bereits aus dem Verschwinden des konstanten Terms und der Orthogonalität bezüglich des Petersson-Skalarprodukts folgt eine nichttriviale obere Abschätzung der Koeffizienten. Mit Hilfe elementarer Fourieranalysis lässt sich die Schranke^[121]

${\displaystyle a_{n}(f)\ll n^{\frac {k}{2}}}$

zeigen. Diese ergibt sich aus der Tatsache, dass ${\displaystyle f(x+iy)\ll y^{-{\frac {k}{2}}}}$ gleichmäßig in ${\displaystyle x}$ angewendet auf das Integral

${\displaystyle a_{n}(f)=e^{2\pi ny}\int _{0}^{1}f(x+iy)e^{-2\pi inx}\mathrm {d} x}$

bei optimaler Wahl ${\displaystyle y={\tfrac {1}{n}}}$.^[121]

Feinere Methoden führen weiter: Mit dem Petersson-Skalarprodukt und der Theorie der Bessel- und Kloosterman-Summen gelang es, nichttriviale Abschätzungen zu gewinnen. Etwa bewies Rankin 1939^[122][123]

${\displaystyle a_{n}(f)\ll n^{{\frac {k}{2}}-{\frac {1}{5}}}}$

was zwar schwächer ist als Delignes scharfe Schranke, aber deutlich stärker als Heckes Abschätzung. Rankins Ergebnis wurde später durch Selberg (für alle ${\displaystyle \varepsilon >0}$) auf

${\displaystyle a_{n}(f)\ll _{\varepsilon }n^{{\frac {k}{2}}-{\frac {1}{4}}+\varepsilon }}$

verbessert, wobei dieser von André Weil gegebene Abschätzungen von Kloosterman-Summen nutzte.^[124] Diese sind gegeben durch^[125]

${\displaystyle \left|K(m,n;c)\right|\leq \sigma _{0}(c)\left(\mathrm {ggT} (m,n,c)c\right)^{\frac {1}{2}}}$

und führen im Falle ${\displaystyle c=p}$ Primzahl mit ${\displaystyle \mathrm {ggT} (p,mn)=1}$ zum berühmten Sepzialfall

${\displaystyle |K(m,n;p)|\leq 2p^{\frac {1}{2}}.}$

Den entscheidenden Fortschritt brachte Delignes Beweis der Weil-Vermutungen, der die scharfe Schranke

${\displaystyle |a_{p}(f)|\leq 2\,p^{\frac {k-1}{2}}}$

für die Fourier-Koeffizienten ${\displaystyle a_{p}(f)}$ von Eigenformen an Primzahlen liefert. Daraus folgt allgemein

${\displaystyle a_{n}(f)\ll _{\varepsilon }n^{{\frac {k-1}{2}}+\varepsilon },}$

was asymptotisch sogar optimal ist.

Zu jeder ganzen Modulform

${\displaystyle f(z)=\sum _{n=0}^{\infty }a_{n}(f)q^{n}}$

vom Gewicht ${\displaystyle k}$ zur vollen Modulgruppe lässt sich eine L-Reihe definieren. Dieses Konzept spielt eine zentrale Rolle in der Zahlentheorie und bildet die Brücke zwischen der Theorie der Modulformen und der klassischen Theorie der Zetafunktionen. Von besonderem Interesse ist der Fall, wenn die L-Reihe ein Euler-Produkt besitzt. Nur^[126] in diesem Fall spricht man auch von einer L-Funktion (siehe auch Selberg-Klasse).^[127] Diese Unterscheidung (L-Reihe und L-Funktion) wird in der Literatur jedoch nicht immer einheitlich gehandhabt – gelegentlich wird in allen Fällen von „L-Funktion“ gesprochen.^[128]

Die L-Reihe von ${\displaystyle f}$ wird durch die Dirichlet-Reihe

${\displaystyle L(f,s):=\sum _{n=1}^{\infty }{\frac {a_{n}(f)}{n^{s}}}}$

definiert. Da für die Fourier-Koeffizienten ganzer Modulformen ${\displaystyle a_{n}(f)\ll n^{k-1}}$ gilt, wird diese Reihe für alle ${\displaystyle \mathrm {Re} (s)>k}$ stets absolut und lokal gleichmäßig konvergieren, und dort eine holomorphe Funktion darstellen. Für Spitzenformen dehnt sich wegen des langsameren Wachstums der Koeffizienten der absolute Konvergenzbereich nach Hecke bis zu ${\displaystyle \mathrm {Re} (s)>{\tfrac {k}{2}}+1}$,^[129] und nach Deligne sogar bis nach ${\displaystyle \mathrm {Re} (s)>{\tfrac {k}{2}}+{\tfrac {1}{2}}}$.^[130]

Ist ${\displaystyle f}$ eine normierte Hecke-Eigenform, so besitzt ${\displaystyle L(f,s)}$ zusätzlich ein Euler-Produkt:^[131]

${\displaystyle L(f,s)=\prod _{p\,{\text{Primzahl}}}{\frac {1}{1-a_{p}(f)p^{-s}+p^{k-1-2s}}}.}$

In diesem Fall spricht man auch von einer Hecke-L-Funktion, oder kurz L-Funktion. Letzteres ist weniger spezifisch, da es auch L-Funktionen zu anderen Objekten als Modulformen gibt. Eine andere Darstellungsmöglichkeit ist

${\displaystyle L(f,s)=\prod _{p\,{\text{Primzahl}}}{\frac {1}{(1-\alpha _{p}p^{-s})(1-\beta _{p}p^{-s})}},}$

wobei die Werte ${\displaystyle \alpha _{p}}$ und ${\displaystyle \beta _{p}}$ die Nullstellen des quadratischen Polynoms ${\displaystyle X^{2}-a_{p}(f)X+p^{k-1}}$ sind, und

${\displaystyle a_{p^{n}}(f)={\frac {\beta _{p}^{n+1}-\alpha _{p}^{n+1}}{\beta _{p}-\alpha _{p}}}}$

erfüllen.^[132]

Das Euler-Produkt bildet das Fundament für die zahlentheoretische Bedeutung der Hecke-Eigenformen.

Mit Hilfe der Mellin-Transformation lässt sich zeigen, dass ${\displaystyle L(f,s)}$ eine meromorphe Fortsetzung auf die gesamte komplexe Ebene besitzt, die sogar holomorph in ganz ${\displaystyle \mathbb {C} \setminus \{k\}}$ ist. In ${\displaystyle s=k}$ hingegen besitzt ${\displaystyle L(f,s)}$ höchstens einen einfachen Pol. Genau dann ist ${\displaystyle f}$ eine Spitzenform, wenn sich ${\displaystyle L(f,s)}$ sogar zu einer ganzen Funktion fortsetzt.^[133] Es gilt stets ${\displaystyle L(f,0)=-a_{0}(f)}$ und ${\displaystyle L(f,n)=0}$ für alle ganzen ${\displaystyle n<0}$.^[134]

Zudem gilt eine Funktionalgleichung. Man definiert dazu die vervollständigte L-Reihe

${\displaystyle \Lambda (f,s)=(2\pi )^{-s}\,\Gamma (s)\,L(f,s).}$

Diese erfüllt die Funktionalgleichung^[135]

${\displaystyle \Lambda (f,s)=(-1)^{\frac {k}{2}}\,\Lambda (f,k-s),}$

und ${\displaystyle \Lambda (f,s)}$ ist auf sämtlichen Vertikalstreifen ${\displaystyle \sigma _{1}\leq \mathrm {Re} (s)\leq \sigma _{2}}$ für ${\displaystyle \mathrm {Im} (s)\to \infty }$ beschränkt.^[134]

Dies ist die exakte Analogie zur Funktionalgleichung der Riemannschen Zetafunktion.^[136]

Der Beweis der Funktionalgleichung, hier exemplarisch für ${\displaystyle f\in {\mathcal {S}}_{k}}$, wird traditionell mittels der Mellin-Transformation geführt. Über die Entwicklung ${\displaystyle f(iy)=\textstyle \sum _{n=1}^{\infty }a_{n}(f)e^{-2\pi ny}}$ ergibt diese

${\displaystyle \Lambda (f,s)=(2\pi )^{-s}\Gamma (s)L(f,s)=\int _{0}^{\infty }f(iy)\,y^{s-1}\,\mathrm {d} y.}$

Die Modularität ${\displaystyle f(-1/z)=z^{k}f(z)}$ liefert für ${\displaystyle y>0}$ die Relation ${\displaystyle f({\tfrac {1}{y}})=i^{k}y^{k}f(iy)}$. Zerlegt man das Integral bei 1 und substituiert ${\displaystyle y\mapsto {\tfrac {1}{y}}}$ im unteren Teil, so erhält man

${\displaystyle \Lambda (f,s)=i^{k}\int _{1}^{\infty }f(iy)\,y^{k-s-1}\mathrm {d} y+\int _{1}^{\infty }f(iy)\,y^{s-1}\mathrm {d} y.}$

Vergleicht man mit der Darstellung von ${\displaystyle \Lambda (f,k-s)}$, so folgt unmittelbar

${\displaystyle \Lambda (f,s)=(-1)^{\frac {k}{2}}\Lambda (f,k-s).}$

Der Hecke-Umkehrsatz besagt, dass jede Dirichlet-Reihe

${\displaystyle L(s)=\sum _{n=1}^{\infty }{\frac {a_{n}}{n^{s}}}}$

die sich zu einer in ganz ${\displaystyle \mathbb {C} \setminus \{k\}}$ holomorphen Funktion fortsetzt mit einem einfachen Pol in ${\displaystyle s=k}$, die entsprechende Funktionalgleichung oben erfüllt, und deren Vervollständigung ${\displaystyle (2\pi )^{-s}\Gamma (s)L(s)}$ auf sämtlichen Vertikalstreifen ${\displaystyle \sigma _{1}\leq \mathrm {Re} (s)\leq \sigma _{2}}$ für ${\displaystyle \mathrm {Im} (s)\to \infty }$ beschränkt ist, tatsächlich von einer Modulform vom Gewicht ${\displaystyle k}$ zur vollen Modulgruppe stammt. Es gibt also eine ganze Modulform ${\displaystyle f}$ des Gewichts ${\displaystyle k}$, sodass ${\displaystyle a_{n}=a_{n}(f)}$ für alle ${\displaystyle n\in \mathbb {N} }$, und ferner^[135]

${\displaystyle a_{0}(f)={\frac {(k-1)!}{(2\pi i)^{k}}}\mathrm {res} _{s=k}L(s).}$

Damit ist der Umkehrsatz von Hecke die Brücke zwischen analytischen Eigenschaften einer L-Reihe und der Existenz einer zugrunde liegenden Modulform. Dieses Prinzip ist in verallgemeinerter Form ein Grundpfeiler des Langlands-Programms.

• Für die Diskriminante ${\displaystyle \Delta (z)=\sum _{n=1}^{\infty }\tau (n)q^{n}}$ ergibt sich^[137]

${\displaystyle L(\Delta ,s)=\sum _{n=1}^{\infty }{\frac {\tau (n)}{n^{s}}}=\prod _{p\,{\text{Primzahl}}}{\frac {1}{1-\tau (p)p^{-s}+p^{11-2s}}}.}$

• Für Eisensteinreihen lassen sich die L-Reihen (bis auf Vorfaktor L-Funktionen) in Produkte klassischer Zetafunktionen zerlegen, zum Beispiel^[138]

${\displaystyle L(E_{k},s)=-{\frac {2k}{B_{k}}}\zeta (s)\,\zeta (s-k+1)=-{\frac {2k}{B_{k}}}\prod _{p\,{\text{Primzahl}}}{\frac {1}{1-(1+p^{k-1})p^{-s}+p^{k-1-2s}}},}$

wobei ${\displaystyle B_{k}}$ die ${\displaystyle k}$-te Bernoulli-Zahl bezeichnet.

Es bezeichnet

${\displaystyle f(z)=\sum _{n=1}^{\infty }a_{n}(f)q^{n}}$

eine normierte Hecke-Eigenform vom Gewicht ${\displaystyle k\geq 2}$ zur vollen Modulgruppe, mit Zahlkörper ${\displaystyle \mathbb {Q} _{f}=\mathbb {Q} (a_{1}(f),a_{2}(f),\dots )}$. Die ganzzahligen Stellen ${\displaystyle 1\leq m\leq k-1}$ der zugehörigen L-Funktion sind die kritischen Werte, da diese nicht wegen eines Gammafaktors verschwinden müssen.

Yuri Manin zeigte, dass es zwei von ${\displaystyle f}$ abhängige, positiv reelle Perioden ${\displaystyle \Omega _{f}^{\pm }}$ gibt, so dass für alle kritischen Werte

${\displaystyle {\frac {L(f,m)}{(2\pi )^{\,m}\,\Omega _{f}^{\varepsilon (m)}}}\;\in \;\mathbb {Q} _{f},\qquad 1\leq m\leq k-1,m\not ={\frac {k}{2}},}$

und

${\displaystyle \Omega _{f}^{+}\Omega _{f}^{-}=\langle f,f\rangle ,}$

wobei das Vorzeichen ${\displaystyle \varepsilon (m)\in \{+,-\}}$ also allein durch die Parität von ${\displaystyle m}$ bestimmt ist (die beiden Familien geradzahliger bzw. ungeradzahliger ${\displaystyle m}$ teilen sich jeweils eine gemeinsame Periode).^[139] Insbesondere sind daher alle Quotienten zweier kritischer Werte nach derselben Normalisierung algebraisch:

${\displaystyle {\frac {L(f,m_{1})}{(2\pi i)^{m_{1}}\,\Omega _{f}^{\varepsilon }}}{\bigg /}{\frac {L(f,m_{2})}{(2\pi i)^{m_{2}}\,\Omega _{f}^{\varepsilon }}}\;\in \;\mathbb {Q} _{f}\quad {\text{für }}m_{1}\equiv m_{2}{\pmod {2}}}$

sofern ${\displaystyle L(f,m_{2})\not =0}$.

Die Rankin–Selberg-Theorie, benannt nach Robert Alexander Rankin und Atle Selberg, liefert eine Methode, um aus zwei Modulformen eine L-Funktion zu konstruieren und deren analytische Eigenschaften zu untersuchen. Sind

${\displaystyle f(z)=\sum _{n=1}^{\infty }a_{n}(f)q^{n}}$ und ${\displaystyle g(z)=\sum _{n=1}^{\infty }a_{n}(g)q^{n}}$ Spitzenformen vom Gewicht ${\displaystyle k}$,

so definiert man

${\displaystyle L(f\otimes g,s):=\sum _{n=1}^{\infty }{\frac {a_{n}(f){\overline {a_{n}(g)}}}{n^{s}}}.}$

Die zentrale Beobachtung ist, dass sich dieses Dirichlet-Reihenprodukt als Mellin-Transformation eines Integrals darstellen lässt. Es gilt die Identität^[140]

${\displaystyle \int _{\Gamma _{\infty }\backslash \mathbb {H} }f(z)\,{\overline {g(z)}}\,y^{s+1}\,{\frac {\mathrm {d} x\,\mathrm {d} y}{y^{2}}}={\frac {\Gamma (s)}{(4\pi )^{s}}}L(f\otimes g,s),}$

wobei ${\displaystyle \Gamma (s)}$ die Gammafunktion und ${\displaystyle \Gamma _{\infty }}$ die Untergruppe aller Translationen in der vollen Modulgruppe bezeichnet. Dadurch überträgt sich die analytische Fortsetzung und die Funktionalgleichung des Integrals auf ${\displaystyle L(f\otimes g,s)}$. Ferner kann auf diese Weise gezeigt werden, dass die Reihe

${\displaystyle \sum _{n=1}^{\infty }{\frac {a_{n}(f){\overline {a_{n}(g)}}}{n^{s}}}}$

für alle Werte ${\displaystyle \mathrm {Re} (s)>k}$ absolut konvergiert, sich meromorph nach ${\displaystyle \mathbb {C} }$ fortsetzen lässt, und in ${\displaystyle s=k}$ einen Pol erster Ordnung besitzt (sofern ${\displaystyle \langle f,g\rangle \not =0}$). Besonders interessant ist dies für den Spezialfall ${\displaystyle f=g}$, der zur klassischen Rankin-Zetafunktion^[141]

${\displaystyle L(f\otimes f,s)=\sum _{n=1}^{\infty }{\frac {|a_{n}(f)|^{2}}{n^{s}}}}$

korrespondiert. Schlüsselidentität ist

${\displaystyle \int _{\Gamma _{\infty }\backslash \mathbb {H} }|f(z)|^{2}\,y^{s+1}\,{\frac {\mathrm {d} x\,\mathrm {d} y}{y^{2}}}=\int _{0}^{\infty }y^{s-1}\left(\int _{0}^{1}|f(x+iy)|^{2}\mathrm {d} x\right)\mathrm {d} y=\sum _{n=1}^{\infty }|a_{n}(f)|^{2}\int _{0}^{\infty }y^{s-1}e^{-4\pi ny}\mathrm {d} y={\frac {\Gamma (s)}{(4\pi )^{s}}}\sum _{n=1}^{\infty }{\frac {|a_{n}(f)|^{2}}{n^{s}}},}$

wobei im zweiten Schritt die Parsevalsche Identität

${\displaystyle \int _{0}^{1}|f(x+iy)|^{2}\mathrm {d} x=\sum _{n=1}^{\infty }|a_{n}(f)|^{2}e^{-4\pi ny}}$

genutzt wurde. Zum Vertauschen von Integral und Summe dient der Satz von Lebesgue und die von Hecke bekannte, in ${\displaystyle x}$ gleichmäßige Abschätzung ${\displaystyle f(x+iy)\ll y^{-{\frac {k}{2}}}}$.^[142] Aus der klassischen Schranke ${\displaystyle a_{n}(f)\ll n^{\frac {k}{2}}}$ von Hecke ist die Konvergenz der Reihe ${\displaystyle L(f\otimes f,s)}$ im Streifen ${\displaystyle k+1\geq \mathrm {Re} (s)>k}$ nicht zu folgern und somit hochgradig nichttrivial.^[143] Ferner ist die Rankin-Zetafunktion eng mit der Norm ${\displaystyle \langle f,f\rangle }$ im Petersson-Skalarprodukt verknüpft, nämlich über das Residuum in ${\displaystyle s=k}$:^[141]

${\displaystyle \langle f,f\rangle ={\frac {\pi }{3}}{\frac {(k-1)!}{(4\pi )^{k}}}\mathrm {res} _{s=k}L(f\otimes f,s).}$

Daraus ergibt sich eine Interpretation der Norm von Eigenformen in Bezug auf spezielle Werte von L-Funktionen.

Eine erste bedeutende Anwendung der Theorie stammt von Rankin aus dem Jahr 1939. Mit Hilfe eines technischen Satzes von Edmund Landau zeigte er^[144]

${\displaystyle \sum _{1\leq n\leq x}|a_{n}(f)|^{2}={\frac {3}{\pi }}{\frac {(4\pi )^{k}}{(k-1)!}}\langle f,f\rangle x^{k}+O\left(x^{k-{\frac {2}{5}}}\right),\qquad (x\to \infty ),}$

wobei eine schwächere Aussage (ohne Fehlerterm) bereits mit einem Taubersatz gewonnen werden kann. Daniel Bump merkte an, man könne dies so interpretieren, dass die scharfe Abschätzung von Deligne „im Durchschnitt“ erfüllt sei.^[145]

Eine weitere Anwendung ist die Eichler-Selberg-Spurformel. Sie liefert eine exakte Formel für die Spur der Hecke-Operatoren ${\displaystyle T_{n}}$ auf dem Raum der Spitzenformen vom Gewicht ${\displaystyle k}$ zur vollen Modulgruppe.^[146]

Modulfunktionen lassen sich durch Erweiterung der Art des Transformationsverhaltens und für andere Gruppen als die Modulgruppe verallgemeinern.

Zunächst wurden oben nur Modulformen zu ganzzahligem Gewicht ${\displaystyle k}$ betrachtet, es gibt aber auch solche zu rationalen Werten, die auch eine Rolle in der Zahlentheorie spielen, so benutzte Jerrold Tunnell Modulformen zum Gewicht ${\displaystyle k=3/2}$ bei der Lösung des Problems kongruenter Zahlen.

Beispielsweise kann man Funktionen betrachten, die sich durch Multiplikation mit einem automorphen Faktor transformieren:

${\displaystyle f\left({\frac {az+b}{cz+d}}\right)=\varepsilon (a,b,c,d)(cz+d)^{k}f(z)}$

mit dem automorphen Faktor ${\displaystyle \varepsilon (a,b,c,d)(cz+d)^{k}}$, wobei ${\displaystyle |\varepsilon (a,b,c,d)|=1}$. Das sind Beispiele für automorphe Funktionen. Ein Beispiel ist die Dedekindsche Etafunktion. In der algebraischen Zahlentheorie werden auch häufig Modulfunktionen zur Kongruenzuntergruppe ${\displaystyle \Gamma _{0}(N)}$ betrachtet mit einem automorphen Faktor, der mit dem Dirichlet-Charakter ${\displaystyle \chi {\pmod {N}}}$ gebildet wird (Modulformen vom Gewicht ${\displaystyle k}$, Nebentypus ${\displaystyle \chi }$ und Stufe ${\displaystyle N}$):

${\displaystyle f\left({\frac {az+b}{cz+d}}\right)=\chi (d)(cz+d)^{k}f(z)}$

Sie sind für ${\displaystyle z}$ in der oberen Halbebene definiert und holomorph in der Spitze.

Automorphe Formen sind für topologische Gruppen ${\displaystyle G}$ (Lie-Gruppen) definiert und deren diskrete Untergruppen ${\displaystyle \Gamma }$. Das entspricht im Fall der Modulformen für die Modulgruppe ${\displaystyle \operatorname {SL} (2,\mathbf {Z} )}$ der Modulgruppe selbst als diskreter Untergruppe der Liegruppe ${\displaystyle \operatorname {SL} (2,\mathbf {R} )}$ oder den Kongruenzuntergruppen als diskreten Untergruppe der Modulgruppe. Das Transformationsgesetz wird hier allgemein mit Automorphiefaktoren definiert. Automorphe Formen sind Eigenfunktionen bestimmter Casimir-Operatoren von ${\displaystyle G}$ (das entspricht bei den Modulfunktionen der Tatsache, dass diese analytische Funktionen in zwei Dimensionen sind, die die Laplacegleichung erfüllen, was dem Casimir-Operator für ${\displaystyle \operatorname {SL} (2,\mathbf {R} )}$ entspricht) und erfüllen wie die Modulformen bestimmte Wachstumsbedingungen. Sie wurden schon im 19. Jahrhundert für Fuchssche Gruppen (diskrete Untergruppen von ${\displaystyle \operatorname {SL} (2,\mathbf {R} )}$) von Henri Poincaré betrachtet und in der Zahlentheorie Anfang des 20. Jahrhunderts von David Hilbert (Hilbertsche Modulformen für total reelle Zahlkörper^[147] ${\displaystyle F}$ zur allgemeinen linearen Gruppe ${\displaystyle GL_{2}^{+}({\mathcal {O}}_{F})}$ über dem Ring der ganzen Zahlen des Zahlkörpers, definiert als Modulform auf dem ${\displaystyle m}$-fachen Produkt der oberen Halbebene, mit ${\displaystyle m}$ als Grad von ${\displaystyle F}$ über den rationalen Zahlen).

Ein weiteres Beispiel automorpher Formen in mehreren komplexen Variablen sind Siegelsche Modulformen, die im siegelschen Halbraum definiert sind und automorphe Formen zur symplektischen Gruppe sind. Sie spielen eine ähnliche Rolle für die Parametrisierung abelscher Varietäten wie Modulformen für die Parametrisierung von elliptischen Funktionen (als jeweilige Modulräume) und wurden von Carl Ludwig Siegel ursprünglich in der Theorie quadratischer Formen betrachtet.

Auch Jacobiformen sind automorphe Funktionen in mehreren Variablen, zu ihnen gehören zum Beispiel die Weierstraßsche ℘-Funktion und die Jacobische Thetafunktion.

Automorphe Formen spielen eine wesentliche Rolle im Langlands-Programm, wo algebraische Gruppen in einem zahlentheoretischen Kontext betrachtet werden (als algebraische Gruppen über dem Adelring eines algebraischen Zahlkörpers) und deren Darstellungstheorie eine besondere Rolle spielt.

Weitere Beispiele von Erweiterungen des Konzepts von Modulformen sind die Mock-Thetafunktionen von S. Ramanujan bzw. Mock-Modulformen. Sie sind selbst keine Modulformen, lassen sich aber durch Addition einer nicht-holomorphen Komponente (Schatten der Mock-Modulform genannt) zu einer Modulform vervollständigen und fanden spektakuläre Anwendung in der Theorie der Partitionen durch Ken Ono, Jan Hendrik Bruinier und Kathrin Bringmann. Sie stehen nach Sander Zwegers in Zusammenhang mit Maaß-Formen bzw. Maaß-Wellenformen von Hans Maaß, nicht-analytischen automorphen Formen, die als Eigenfunktionen des invarianten (hyperbolischen) Laplace-Operators zum Gewicht ${\displaystyle k}$ sind. Mock-Modulformen sind der holomorphe Anteil einer schwachen Maaßform, wobei sich das schwach auf die verlangten Wachstumsbedingungen bezieht.^[148]

Siegelsche und Hilbertsche Modulformen und Modulkurven sind Beispiele für Shimura-Varietäten.

• Tom M. Apostol: Modular Functions and Dirichlet Series in Number Theory. 2. Auflage. Springer Science+Business Media, Berlin 1990, ISBN 3-540-97127-0.
• Siegfried Bosch: Algebra. 10. Auflage. Springer Spektrum, Berlin/Heidelberg 2023, ISBN 978-3-662-67463-5.
• Kathrin Bringmann, Amanda Folsom, Ken Ono, Larry Rolen: Harmonic Maass Forms and Mock Modular Forms: Theory and Applications. (= Colloquium Publications. Band 64). American Mathematical Society, Providence, Rhode Island 2017, ISBN 978-1-4704-1944-8.
• Jan Hendrik Bruinier, Gerard van der Geer, Günter Harder, Don Zagier: The 1-2-3 of Modular Forms. Lectures at a Summer School in Nordfjordeid, Norway. Springer-Verlag, Berlin/ Heidelberg 2008, ISBN 978-3-540-74117-6.
• Daniel Bump: Automorphic forms and representations. Cambridge University Press, Cambridge 1998, ISBN 0-521-65818-7.
• Paul J. McCarthy: Arithmetische Funktionen. Springer Vieweg, Berlin/ Heidelberg 2016, ISBN 978-3-662-53731-2.
• Henri Cohen: Elliptic Curves. In: M. Waldschmidt, P. Moussa, J.-M. Luck, C. Itzykson: From Number Theory to Physics. Second Corrected Printing. Springer-Verlag, Berlin/ Heidelberg/ New York 1995, ISBN 3-540-53342-7, Kapitel 3, S. 212–237.
• Henri Cohen: Number Theory. Volume I: Tools and Diophantine Equations. Springer-Verlag, New York 2007, ISBN 978-0-387-49922-2.
• Henri Cohen: Number Theory. Volume II: Analytic and Modern Tools. Springer-Verlag, New York 2007, ISBN 978-0-387-49893-5.
• Henri Cohen, Fredrik Strömberg: Modular Forms. A Classical Approach. (= Graduate Studies in Mathematics. Band 179). American Mathematical Society, Providence, Rhode Island 2017, ISBN 978-0-8218-4947-7.
• Gary Cornell, Joseph H. Silverman, Glenn Stevens (Hrsg.): Modular Forms and Fermat’s Last Theorem. Springer-Verlag, New York 1997, ISBN 0-387-94609-8.
• Henri Darmon: Rational points on modular elliptic curves. Regional Conference Series in Mathematics, American Mathematical Society, Number 101.
• Anton Deitmar: Automorphe Formen. Springer-Lehrbuch Masterclass. Springer, Berlin/ Heidelberg 2010, ISBN 978-3-642-12389-4.
• Fred Diamond, Jerry Shurman: A First Course in Modular Forms. Springer-Verlag, New York 2005, ISBN 0-387-23229-X.
• Bas Edixhoven, Gerard van der Geer, Ben Moonen: Modular Forms. In: Bas Edixhoven, Gerard van der Geer, Ben Moonen (Hrsg.): Modular Forms on Schiermonnikoog. Cambridge University Press, Cambridge. Chapter 1, Seiten 1–12. ISBN 978-0-521-49354-3.
• Eberhard Freitag, Rolf Busam: Funktionentheorie 1. 4. Auflage. Springer-Verlag, Berlin/ Heidelberg 2006, ISBN 3-540-31764-3.
• Godfrey Harold Hardy, Edward Maitland Wright: An Introduction to the Theory of Numbers. 6. Auflage. Edited by Roger Heath-Brown, Joseph Silverman, and Andrew Wiles. Oxford University Press, Oxford 2008, ISBN 978-0-19-921986-5.
• Peter Henrici: Applied and Computational Complex Analysis. Volume 2: Special Functions - Integral-Transforms - Asymptotics - Continued Fractions. John Wiley & Sons, New York London Sydney Toronto 1977, ISBN 0-471-01525-3.
• Lloyd J. P. Kilford: Modular Forms: A Classical and Computational Introduction. Imperial College Press, London, 2008, ISBN 978-1-84816-213-6.
• Neal Koblitz: Introduction to elliptic curves and modular forms. Springer-Verlag, Berlin 1984, ISBN 3-540-96029-5.
• Max Koecher, Aloys Krieg: Elliptische Funktionen und Modulformen. 2. Auflage. Springer-Verlag, Berlin/ Heidelberg 2007, ISBN 978-3-540-49324-2.
• Jacob Korevaar: Tauberian Theory: A Century of Developments. (= Grundlehren der Mathematischen Wissenschaften. Band 329). Springer-Verlag, Berlin/ Heidelberg 2004, ISBN 3-540-21058-X.
• Dimitris Koukoulopoulos: The Distribution of Prime Numbers. (= Graduate Studies in Mathematics. Vol. 203). American Mathematical Society, Providence, Rhode Island 2019, ISBN 978-1-4704-6285-7.
• Serge Lang: Introduction to Modular forms. (= Grundlehren der mathematischen Wissenschaften. Band 222). Springer-Verlag, Berlin/Heidelberg 1976, ISBN 3-540-07833-9.
• Toshitsune Miyake: Modular forms. Springer-Verlag, Berlin/ Heidelberg 1989, ISBN 3-540-50268-8.
• M. Ram Murty, V. Kumar Murty: The Mathematical Legacy of Srinivasa Ramanujan. Springer, Berlin Heidelberg, 2013. ISBN 978-81-322-0769-6.
• David E. Rohrlich: Modular Curves, Hecke Correspondences, and L-functions. In: Gary Cornell, Joseph H. Silverman, Glenn Stevens (Hrsg.): Modular Forms and Fermat’s Last Theorem. Springer-Verlag, New York, 1997. Chapter III, Seiten 41–100. ISBN 978-1-4612-1844-5.
• Jean-Pierre Serre: A Course in Arithmetic. Graduate Texts in Mathematics, Band 7. Springer-Verlag, New York Heidelberg Berlin, 1973. ISBN 978-0-387-90040-7.
• Joseph H. Silverman: Advanced Topics in the Arithmetic of Elliptic Curves. Graduate Texts in Mathematics, Vol. 151. Springer-Verlag, New York, 1994. ISBN 978-0-387-94328-1.
• Joseph H. Silverman, John Tate: Rational points on elliptic curves. Springer-Verlag, New York 1992, ISBN 0-387-97825-9.
• Elias Stein, Rami Shakarchi: Fourier Analysis. Princeton University Press, Princeton New Jersey 2003, ISBN 0-691-11384-X.
• William Stein: Modular Forms, a Computational Approach. (= Graduate Studies in Mathematics. Vol. 79). With an appendix by Paul E. Gunnells. American Mathematical Society, Providence 2007, ISBN 978-0-8218-3960-7.
• Don Zagier: Introduction to Modular Forms. In: M. Waldschmidt, P. Moussa, J.-M. Luck, C. Itzykson: From Number Theory to Physics. Second Corrected Printing. Springer-Verlag, Berlin/ Heidelberg/ New York 1995, ISBN 3-540-53342-7, Kapitel 4, S. 238–291 Online, PDF.

• Gabor Wiese, verschiedene Vorlesungen zu Modulformen
• The L-functions and modular forms data base

1. ↑ Durch den Variablenwechsel ${\displaystyle x\mapsto u_{1}x+u_{2}}$ und ${\displaystyle y\mapsto v_{1}x+v_{2}y+v_{3}}$ mit ${\displaystyle u_{1},v_{2}}$ Einheiten, werden auch Kurven der allgemeineren Form ${\displaystyle y^{2}+a_{1}xy+a_{3}y=a_{0}x^{3}+a_{2}x^{2}+a_{4}x+a_{6}}$ mit einer Einheit ${\displaystyle a_{0}}$ einbezogen.
2. ↑ Es sind ${\displaystyle a,b,c}$ in Wahrheit nicht völlig beliebig: Es soll die Diskriminante des Polynoms ${\displaystyle x^{3}+ax^{2}+bx+c}$ nicht Null sein.

1. ↑ Anton Deitmar: Automorphe Formen. Berlin/ Heidelberg 2010, S. 16.
2. ↑ ^{a b c} Jan Hendrik Bruinier, Gerard van der Geer, Günter Harder, Don Zagier: The 1-2-3 of Modular Forms. Berlin/ Heidelberg 2008, S. 3.
3. ↑ William Stein: Modular Forms, a Computational Approach. Providence, RI., 2007, S. 1.
4. ↑ Elias Wegert: Visualization of Complex Functions – Plea for the Phase Plot –, Technical University Freiberg, 2009, S. 1.
5. ↑ Siegfried Bosch: Algebra. 8. Auflage. Berlin/Heidelberg 2013, S. 11.
6. ↑ Anton Deitmar: Automorphe Formen. Berlin/ Heidelberg 2010, S. 15.
7. ↑ Henri Cohen: Elliptic Curves. In: M. Waldschmidt, P. Moussa, J.-M. Luck, C. Itzykson: From Number Theory to Physics. Berlin/ Heidelberg/ New York Second Corrected Printing 1995, S. 226–227.
8. ↑ ^{a b} Eberhard Freitag, Rolf Busam: Funktionentheorie 1. 4. Auflage. Berlin/ Heidelberg 2006, S. 321.
9. ↑ Sadiah Zahoor: Congruences Related to Hilbert Modular Forms of Integer and Half-Integer Weights. PhD Thesis, School of Mathematics and Statistics, University of Sheffield, 2022, S. 9.
10. ↑ Elias Stein, Rami Shakarchi: Complex analysis. Princeton (NJ) 2003, S. 43.
11. ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1. 4. Auflage. Berlin/ Heidelberg 2006, S. 374.
12. ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1. 4. Auflage. Berlin/ Heidelberg 2006, S. 341.
13. ↑ Jan Hendrik Bruinier, Gerard van der Geer, Günter Harder, Don Zagier: The 1-2-3 of Modular Forms. Berlin/ Heidelberg 2008, S. 12.
14. ↑ ^{a b c} Don Zagier: Introduction to Modular Forms. In: M. Waldschmidt, P. Moussa, J.-M. Luck, C. Itzykson: From Number Theory to Physics. Berlin/ Heidelberg/ New York 1995, S. 239.
15. ↑ ^{a b} Paul J. McCarthy: Arithmetische Funktionen. Berlin/ Heidelberg 2016, S. 11.
16. ↑ Paul J. McCarthy: Arithmetische Funktionen. Berlin/ Heidelberg 2016, S. 5.
17. ↑ Paul J. McCarthy: Arithmetische Funktionen. Berlin/ Heidelberg 2016, S. 6.
18. ↑ Paul J. McCarthy: Arithmetische Funktionen. Berlin/ Heidelberg 2016, S. 7.
19. ↑ Dimitris Koukoulopoulos: The Distribution of Prime Numbers. Providence, Rhode Island, 2019, S. 52.
20. ↑ Godfrey Harold Hardy, Edward Maitland Wright: An Introduction to the Theory of Numbers. 6. Auflage. Oxford 2008, S. 361.
21. ↑ Godfrey Harold Hardy, Edward Maitland Wright: An Introduction to the Theory of Numbers. 6. Auflage. Oxford 2008, S. 363.
22. ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1. 4. Auflage. Berlin/ Heidelberg 2006, S. 151.
23. ↑ Peter Henrici: Applied and Computational Complex Analysis. Volume 2: Special Functions - Integral-Transforms - Asymptotics - Continued Fractions. New York London Sydney Toronto 1977, S. 442 ff.
24. ↑ M. Ram Murty, V. Kumar Murty: The Mathematical Legacy of Srinivasa Ramanujan. Berlin Heidelberg, 2013, S. 67 ff.
25. ↑ Jacob Korevaar: Tauberian Theory: A Century of Developments. Berlin/ Heidelberg 2004, S. 1 ff.
26. ↑ Jan Hendrik Bruinier, Gerard van der Geer, Günter Harder, Don Zagier: The 1-2-3 of Modular Forms. Berlin/ Heidelberg 2008, S. 15.
27. ↑ Elias Stein, Rami Shakarchi: Fourier Analysis. Princeton New Jersey 2003, S. 139.
28. ↑ ^{a b c} Jan Hendrik Bruinier, Gerard van der Geer, Günter Harder, Don Zagier: The 1-2-3 of Modular Forms. Berlin/ Heidelberg 2008, S. 25.
29. ↑ Jan Hendrik Bruinier, Gerard van der Geer, Günter Harder, Don Zagier: The 1-2-3 of Modular Forms. Berlin/ Heidelberg 2008, S. 26.
30. ↑ Paul J. McCarthy: Arithmetische Funktionen. Berlin/ Heidelberg 2016, S. 133.
31. ↑ Dimitris Koukoulopoulos: The Distribution of Prime Numbers. Providence, Rhode Island, 2019, S. 54.
32. ↑ Dimitris Koukoulopoulos: The Distribution of Prime Numbers. Providence, Rhode Island, 2019, S. 57.
33. ↑ Dimitris Koukoulopoulos: The Distribution of Prime Numbers. Providence, Rhode Island, 2019, S. 84–91.
34. ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1. 4. Auflage. Berlin/ Heidelberg 2006, S. 429.
35. ↑ Dimitris Koukoulopoulos: The Distribution of Prime Numbers. Providence, Rhode Island, 2019, S. 64–65.
36. ↑ ^{a b c} Dimitris Koukoulopoulos: The Distribution of Prime Numbers. Providence, Rhode Island, 2019, S. 65.
37. ↑ Dimitris Koukoulopoulos: The Distribution of Prime Numbers. Providence, Rhode Island, 2019, S. 92.
38. ↑ Houzel: Elliptische Funktionen und Abelsche Integrale. In: Dieudonné: Geschichte der Mathematik. Vieweg, 1985, S. 486 f.
39. ↑ Anton Deitmar: Automorphe Formen. Berlin/ Heidelberg 2010, S. 21.
40. ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1. 4. Auflage. Berlin/ Heidelberg 2006, S. 334.
41. ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1. 4. Auflage. Berlin/ Heidelberg 2006, S. 325.
42. ↑ Max Koecher, Aloys Krieg: Elliptische Funktionen und Modulformen. Berlin/ Heidelberg 2007, S. 124.
43. ↑ Max Koecher, Aloys Krieg: Elliptische Funktionen und Modulformen. Berlin/ Heidelberg 2007, S. 125.
44. ↑ ^{a b} Henri Cohen, Fredrik Strömberg: Modular Forms. A Classical Approach. Providence, Rhode Island 2017, S. 116.
45. ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1. 4. Auflage. Berlin/ Heidelberg 2006, S. 335 ff.
46. ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1. 4. Auflage. Berlin/ Heidelberg 2006, S. 325 ff.
47. ↑ Max Koecher, Aloys Krieg: Elliptische Funktionen und Modulformen. Berlin/ Heidelberg 2007, S. 154–156.
48. ↑ Max Koecher, Aloys Krieg: Elliptische Funktionen und Modulformen. Berlin/ Heidelberg 2007, S. 155.
49. ↑ Max Koecher, Aloys Krieg: Elliptische Funktionen und Modulformen. Berlin/ Heidelberg 2007, S. 156.
50. ↑ Max Koecher, Aloys Krieg: Elliptische Funktionen und Modulformen. Berlin/ Heidelberg 2007, S. 152.
51. ↑ Die erweiterte obere Halbebene besteht aus ${\displaystyle \mathbb {H} }$, ${\displaystyle \mathbb {Q} }$ und ${\displaystyle \infty }$. Die rationalen Zahlen erscheinen, da für ${\displaystyle z\to \infty }$ der Orbit durch Wirkung der Kongruenzuntergruppen im Unendlichen durch ${\displaystyle {\frac {a}{c}}}$ im Unendlichen geht.
52. ↑ Henri Cohen: Elliptic Curves. In: M. Waldschmidt, P. Moussa, J.-M. Luck, C. Itzykson: From Number Theory to Physics. Berlin/ Heidelberg/ New York Second Corrected Printing 1995, S. 213.
53. ↑ Henri Cohen: Elliptic Curves. In: M. Waldschmidt, P. Moussa, J.-M. Luck, C. Itzykson: From Number Theory to Physics. Berlin/ Heidelberg/ New York Second Corrected Printing 1995, S. 214.
54. ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1. 4. Auflage. Berlin/ Heidelberg 2006, S. 318–323.
55. ↑ Max Koecher, Aloys Krieg: Elliptische Funktionen und Modulformen. Berlin/ Heidelberg 2007, S. 159.
56. ↑ William Stein: Modular Forms, a Computational Approach. Providence, RI., 2007, S. 13.
57. ↑ William Stein: Modular Forms, a Computational Approach. Providence, RI., 2007, S. 17.
58. ↑ Max Koecher, Aloys Krieg: Elliptische Funktionen und Modulformen. Berlin/ Heidelberg 2007, S. 160.
59. ↑ Max Koecher, Aloys Krieg: Elliptische Funktionen und Modulformen. Berlin/ Heidelberg 2007, S. 161.
60. ↑ William Stein: Modular Forms, a Computational Approach. Providence, RI., 2007, S. 16.
61. ↑ ^{a b} Don Zagier: Introduction to Modular Forms. In: M. Waldschmidt, P. Moussa, J.-M. Luck, C. Itzykson: From Number Theory to Physics. Berlin/ Heidelberg/ New York 1995, S. 241.
62. ↑ Don Zagier: Introduction to Modular Forms. In: M. Waldschmidt, P. Moussa, J.-M. Luck, C. Itzykson: From Number Theory to Physics. Berlin/ Heidelberg/ New York 1995, S. 283–284.
63. ↑ Anton Deitmar: Automorphe Formen. Berlin/ Heidelberg 2010, S. 30.
64. ↑ Max Koecher, Aloys Krieg: Elliptische Funktionen und Modulformen. Berlin/ Heidelberg 2007, S. 163.
65. ↑ Don Zagier: Introduction to Modular Forms. In: M. Waldschmidt, P. Moussa, J.-M. Luck, C. Itzykson: From Number Theory to Physics. Berlin/ Heidelberg/ New York 1995, S. 242.
66. ↑ Don Zagier: Introduction to Modular Forms. In: M. Waldschmidt, P. Moussa, J.-M. Luck, C. Itzykson: From Number Theory to Physics. Berlin/ Heidelberg/ New York 1995, S. 243.
67. ↑ Daniel Bump: Automorphic forms and representations. Cambridge 1998, S. 2.
68. ↑ Max Koecher, Aloys Krieg: Elliptische Funktionen und Modulformen. Berlin/ Heidelberg 2007, S. 164.
69. ↑ Peter Sarnak: Problems of the Millennium: The Riemann Hypothesis (Memento vom 13. April 2016 im Internet Archive), Princeton University & Courant Institute of Math. Sciences, S. 1–3.
70. ↑ Peter Sarnak: Problems of the Millennium: The Riemann Hypothesis (Memento vom 13. April 2016 im Internet Archive), Princeton University & Courant Institute of Math. Sciences, S. 3.
71. ↑ Roger Heath-Brown: The Average Analytic Rank of Elliptic Curves. Duke Mathematical Journal. 122 (3), 2004, S. 591–623.
72. ↑ Zev Klagsbrun, Travis Sherman, James Weigandt: The Elkies curve has rank 28 subject only to GRH. Math. Comput. 88(316), (2019): 837–846.
73. ↑ Peter Bundschuh: Einführung in die Zahlentheorie, 6. Auflage, Springer, S. 71–72.
74. ↑ Joseph H. Silverman, John Tate: Rational points on elliptic curves. New York 1992, S. 183.
75. ↑ Joseph H. Silverman, John Tate: Rational points on elliptic curves. New York 1992, S. 184.
76. ↑ ^{a b} Joseph H. Silverman, John Tate: Rational points on elliptic curves. New York 1992, S. 185.
77. ↑ Henri Cohen: Number theory. Volume I: Tools and Diophantine Equations. New York 2007, S. 586.
78. ↑ Jan Hendrik Bruinier, Gerard van der Geer, Günter Harder, Don Zagier: The 1-2-3 of Modular Forms. Berlin/Heidelberg, S. 69.
79. ↑ Jan Hendrik Bruinier, Gerard van der Geer, Günter Harder, Don Zagier: The 1-2-3 of Modular Forms. Berlin/Heidelberg, S. 67–68.
80. ↑ Jan Hendrik Bruinier, Gerard van der Geer, Günter Harder, Don Zagier: The 1-2-3 of Modular Forms. Berlin/Heidelberg, S. 67.
81. ↑ ^{a b} Jan Hendrik Bruinier, Gerard van der Geer, Günter Harder, Don Zagier: The 1-2-3 of Modular Forms. Berlin/Heidelberg, S. 73.
82. ↑ Henri Cohen: Elliptic Curves. In: M. Waldschmidt, P. Moussa, J.-M. Luck, C. Itzykson: From Number Theory to Physics. Berlin/ Heidelberg/ New York Second Corrected Printing 1995, S. 226.
83. ↑ Henri Cohen: Elliptic Curves. In: M. Waldschmidt, P. Moussa, J.-M. Luck, C. Itzykson: From Number Theory to Physics. Berlin/ Heidelberg/ New York Second Corrected Printing 1995, S. 225.
84. ↑ Nayandeep Deka Baruah, Bruce Berndt, Heng Huat Chan: Ramanujan’s series for ${\displaystyle 1/\pi }$: A survey. Mathematics Student, S. 576.
85. ↑ Alexander J. Yee: y-cruncher - A Multi-Threaded Pi-Program. In: numberworld.org. 10. August 2025, abgerufen am 19. September 2025 (englisch). 
86. ↑ ^{a b} Jan Hendrik Bruinier, Gerard van der Geer, Günter Harder, Don Zagier: The 1-2-3 of Modular Forms. Berlin/Heidelberg, S. 84.
87. ↑ Henri Cohen: Number theory. Volume II: Analytic and Modern Tools. New York 2007, S. 223.
88. ↑ Astronomers Capture First Image of a Black Hole. Event Horizon Telescope (EHT), abgerufen am 14. April 2019 (englisch). 
89. ↑ Fred Diamond, Jerry Shurman: A First Course in Modular Forms. Springer, S. xi–xii.
90. ↑ ^{a b} Max Koecher, Aloys Krieg: Elliptische Funktionen und Modulformen. Berlin/ Heidelberg 2007, S. 154.
91. ↑ Anton Deitmar: Automorphe Formen. Berlin/ Heidelberg 2010, S. 28.
92. ↑ Fred Diamond, Jerry Shurman: A First Course in Modular Forms. New York 2005, S. 17.
93. ↑ William Stein: Modular Forms, a Computational Approach. Providence, RI., 2007, S. 18.
94. ↑ William Stein: Modular Forms, a Computational Approach. Providence, RI., 2007, S. 17.
95. ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1. 4. Auflage. Berlin/ Heidelberg 2006, S. 336.
96. ↑ Max Koecher, Aloys Krieg: Elliptische Funktionen und Modulformen. Berlin/ Heidelberg 2007, S. 173.
97. ↑ Max Koecher, Aloys Krieg: Elliptische Funktionen und Modulformen. Berlin/ Heidelberg 2007, S. 154.
98. ↑ Eberhard Freitag, Rolf Busam: Funktionentheorie 1. 4. Auflage. Berlin/ Heidelberg 2006, S. 336.
99. ↑ Joseph H. Silverman: Advanced Topics in the Arithmetic of Elliptic Curves. New York, 1994, S. 30–31.
100. ↑ Max Koecher, Aloys Krieg: Elliptische Funktionen und Modulformen. Berlin/ Heidelberg 2007, S. 174.
101. ↑ Don Zagier: Introduction to Modular Forms. In: M. Waldschmidt, P. Moussa, J.-M. Luck, C. Itzykson: From Number Theory to Physics. Berlin/ Heidelberg/ New York 1995, S. 240.
102. ↑ Anton Deitmar: Automorphe Formen. Berlin/ Heidelberg 2010, S. 29.
103. ↑ Henri Cohen, Fredrik Strömberg: Modular Forms. A Classical Approach. Providence, Rhode Island 2017, S. 180–181.
104. ↑ Max Koecher, Aloys Krieg: Elliptische Funktionen und Modulformen. Berlin/ Heidelberg 2007, S. 177.
105. ↑ Henri Cohen, Fredrik Strömberg: Modular Forms. A Classical Approach. Providence, Rhode Island 2017, S. 138.
106. ↑ Don Zagier: Introduction to Modular Forms. In: M. Waldschmidt, P. Moussa, J.-M. Luck, C. Itzykson: From Number Theory to Physics. Berlin/ Heidelberg/ New York 1995, S. 255.
107. ↑ Anton Deitmar: Automorphe Formen. Berlin/ Heidelberg 2010, S. 40.
108. ↑ ^{a b c} Don Zagier: Introduction to Modular Forms. In: M. Waldschmidt, P. Moussa, J.-M. Luck, C. Itzykson: From Number Theory to Physics. Berlin/ Heidelberg/ New York 1995, S. 254.
109. ↑ Anton Deitmar: Automorphe Formen. Berlin/ Heidelberg 2010, S. 40.
110. ↑ ^{a b c} Don Zagier: Introduction to Modular Forms. In: M. Waldschmidt, P. Moussa, J.-M. Luck, C. Itzykson: From Number Theory to Physics. Berlin/ Heidelberg/ New York 1995, S. 256.
111. ↑ Don Zagier: Introduction to Modular Forms. In: M. Waldschmidt, P. Moussa, J.-M. Luck, C. Itzykson: From Number Theory to Physics. Berlin/ Heidelberg/ New York 1995, S. 255–256.
112. ↑ Don Zagier: Introduction to Modular Forms. In: M. Waldschmidt, P. Moussa, J.-M. Luck, C. Itzykson: From Number Theory to Physics. Berlin/ Heidelberg/ New York 1995, S. 259.
113. ↑ Henri Cohen, Fredrik Strömberg: Modular Forms. A Classical Approach. Providence, Rhode Island 2017, S. 373–374.
114. ↑ Henri Cohen, Fredrik Strömberg: Modular Forms. A Classical Approach. Providence, Rhode Island 2017, S. 270.
115. ↑ Henri Cohen, Fredrik Strömberg: Modular Forms. A Classical Approach. Providence, Rhode Island 2017, S. 351.
116. ↑ Don Zagier: Introduction to Modular Forms. In: M. Waldschmidt, P. Moussa, J.-M. Luck, C. Itzykson: From Number Theory to Physics. Berlin/ Heidelberg/ New York 1995, S. 257.
117. ↑ ^{a b c d e f} Kathrin Bringmann, Amanda Folsom, Ken Ono, Larry Rolen: Harmonic Maass Forms and Mock Modular Forms: Theory and Applications. Providence, Rhode Island 2017, S. 94.
118. ↑ Kathrin Bringmann, Amanda Folsom, Ken Ono, Larry Rolen: Harmonic Maass Forms and Mock Modular Forms: Theory and Applications. Providence, Rhode Island 2017, S. 91.
119. ↑ Henri Cohen, Fredrik Strömberg: Modular Forms. A Classical Approach. Providence, Rhode Island 2017, S. 314.
120. ↑ Anton Deitmar: Automorphe Formen. Berlin/ Heidelberg 2010, S. 31.
121. ↑ ^{a b} Jan Hendrik Bruinier, Gerard van der Geer, Günter Harder, Don Zagier: The 1-2-3 of Modular Forms. Berlin/ Heidelberg 2008, S. 23.
122. ↑ Henri Cohen, Fredrik Strömberg: Modular Forms. A Classical Approach. Providence, Rhode Island 2017, S. 438.
123. ↑ M. Ram Murty, V. Kumar Murty: The Mathematical Legacy of Srinivasa Ramanujan. Berlin Heidelberg, 2013, S. 56.
124. ↑ Don Zagier: Introduction to Modular Forms. In: M. Waldschmidt, P. Moussa, J.-M. Luck, C. Itzykson: From Number Theory to Physics. Berlin/ Heidelberg/ New York 1995, S. 261.
125. ↑ Henri Cohen, Fredrik Strömberg: Modular Forms. A Classical Approach. Providence, Rhode Island 2017, S. 315.
126. ↑ David E. Rohrlich: Modular Curves, Hecke Correspondences, and L-functions. In: Gary Cornell, Joseph H. Silverman, Glenn Stevens (Hrsg.): Modular Forms and Fermat’s Last Theorem. New York, 1997, S. 78.
127. ↑ Henri Cohen: Number Theory. Volume II: Analytic and Modern Tools. New York, 2007, S. 241.
128. ↑ Anton Deitmar: Automorphe Formen. Berlin/ Heidelberg 2010, S. 32.
129. ↑ Don Zagier: Introduction to Modular Forms. In: M. Waldschmidt, P. Moussa, J.-M. Luck, C. Itzykson: From Number Theory to Physics. Berlin/ Heidelberg/ New York 1995, S. 260–261.
130. ↑ Henri Cohen, Fredrik Strömberg: Modular Forms. A Classical Approach. Providence, Rhode Island 2017, S. 369.
131. ↑ Don Zagier: Introduction to Modular Forms. In: M. Waldschmidt, P. Moussa, J.-M. Luck, C. Itzykson: From Number Theory to Physics. Berlin/ Heidelberg/ New York 1995, S. 259.
132. ↑ Henri Cohen, Fredrik Strömberg: Modular Forms. A Classical Approach. Providence, Rhode Island 2017, S. 374.
133. ↑ Jan Hendrik Bruinier, Gerard van der Geer, Günter Harder, Don Zagier: The 1-2-3 of Modular Forms. Berlin/ Heidelberg 2008, S. 41.
134. ↑ ^{a b} Henri Cohen, Fredrik Strömberg: Modular Forms. A Classical Approach. Providence, Rhode Island 2017, S. 389.
135. ↑ ^{a b} Don Zagier: Introduction to Modular Forms. In: M. Waldschmidt, P. Moussa, J.-M. Luck, C. Itzykson: From Number Theory to Physics. Berlin/ Heidelberg/ New York, 1995, S. 260.
136. ↑ Henri Cohen, Fredrik Strömberg: Modular Forms. A Classical Approach. Providence, Rhode Island 2017, S. 397.
137. ↑ Don Zagier: Introduction to Modular Forms. In: M. Waldschmidt, P. Moussa, J.-M. Luck, C. Itzykson: From Number Theory to Physics. Berlin/ Heidelberg/ New York 1995, S. 259–260.
138. ↑ Don Zagier: Introduction to Modular Forms. In: M. Waldschmidt, P. Moussa, J.-M. Luck, C. Itzykson: From Number Theory to Physics. Berlin/ Heidelberg/ New York 1995, S. 260.
139. ↑ Henri Cohen, Fredrik Strömberg: Modular Forms. A Classical Approach. Providence, Rhode Island 2017, S. 381.
140. ↑ Henri Cohen, Fredrik Strömberg: Modular Forms. A Classical Approach. Providence, Rhode Island 2017, S. 431.
141. ↑ ^{a b} Don Zagier: Introduction to Modular Forms. In: M. Waldschmidt, P. Moussa, J.-M. Luck, C. Itzykson: From Number Theory to Physics. Berlin/ Heidelberg/ New York 1995, S. 270.
142. ↑ Henri Cohen, Fredrik Strömberg: Modular Forms. A Classical Approach. Providence, Rhode Island 2017, S. 431–432.
143. ↑ Henri Cohen, Fredrik Strömberg: Modular Forms. A Classical Approach. Providence, Rhode Island 2017, S. 434.
144. ↑ Henri Cohen, Fredrik Strömberg: Modular Forms. A Classical Approach. Providence, Rhode Island 2017, S. 438.
145. ↑ Daniel Bump: Automorphic forms and representations. Cambridge 1998, S. 75.
146. ↑ Don Zagier: Introduction to Modular Forms. In: M. Waldschmidt, P. Moussa, J.-M. Luck, C. Itzykson: From Number Theory to Physics. Berlin/ Heidelberg/ New York 1995, S. 273–274.
147. ↑ Erzeugt als Erweiterung der rationalen Zahlen durch Adjunktion einer Wurzel ${\displaystyle q}$ eines ganzzahligen Polynoms mit ${\displaystyle m}$ reellen Wurzeln.
148. ↑ Amanda Folsom: What is a mock theta modular form? Notices AMS, Dezember 2010, PDF.