Ausnahmefachwerk

Ein Ausnahmefachwerk ist ein Fachwerk, bei dem sich trotz genügender Stabzahl und sonst geeigneter Gliederung wegen der besonderen Lage, in der sich die Knotenpunkte gegeneinander befinden, keine steifen und gegen beliebige Belastungen widerstandsfähigen Stabverbände bilden.^[1]:212

Ein Beispiel ist im Bild dargestellt, wo sieben Stäbe (schwarz) in den Knoten A bis E gelenkig miteinander und mit den Lagern A und B verbunden sind.^[2]:151 Wenn D nicht auf der Geraden CE liegt, ist das Fachwerk stabil. Im Bild sind jedoch C, D und E kollinear, sodass die Stäbe CD und DE nur horizontale Stabkräfte abtragen können und der vertikalen Kraft F (rot) nichts entgegenzusetzen haben. Ein Gleichgewicht ist in dieser Ausgangslage nicht möglich, was in der Fachwerktheorie zu Problemen führt, siehe #Problematik.

Durch die Kraft kommt es zu einer merklichen Verschiebung infolge einer vergleichsweise unmerklich kleinen Längung der Stäbe (grau), was Beweglichkeit im Kleinen genannt wird^[2] und Ausnahmefachwerke definiert, siehe #Statische Bestimmtheit. Das Ausnahmefachwerk ist gegenüber einem konstruktiv ähnlichen aber stabilen Fachwerk nur in geringem Maß widerstandsfähig, weswegen die stabilen Fachwerke bevorzugt werden.^[1]:214

Bei vielen Anwendungen im technischen Bereich liegen kleine Verformungen vor oder sie müssen aus sicherheitstechnischen Gründen klein gehalten werden. Die im technischen Bereich weit verbreitete geometrisch lineare Betrachtung vernachlässigt alle Deformationsgrößen zweiter und höherer Ordnung, oben die Längung infolge eines (infinitesimal) kleinen Durchhangs. Diese #Theorie erster Ordnung führt in Ausnahmefachwerken zu Problemen.

Ausnahmefachwerke haben in der Entwicklung der Fachwerktheorie eine wichtige Rolle gespielt.^[1]:212

Die Fachwerktheorie befasst sich in erster Linie mit Fachwerken, die sich im Gleichgewicht befinden und bei denen nur kleine Verschiebungen erlaubt sind. Hier vereinfacht sich die mathematische Behandlung erheblich durch zwei Annahmen:

• die Theorie erster Ordnung, die auf geometrischer Linearisierung der nichtlinearen Gleichungen beruhrt, wonach nur (infinitesimal) kleine vernachlässigbare Verschiebungen auftreten, und
• das Erstarrungsprinzip, nach dem ein System im Gleichgewicht bleibt, wenn Teile von ihm erstarren.^[2]:12

Diese vielfach bewährten Annahmen führen beim Ausnahmefachwerk zu Problemen, weil sie im Ausgangszustand ohne signifikante Verschiebungen der Knoten kein Gleichgewicht finden oder nur mit unendlich großen Kräften annähern können.

Die Probleme in der mathematischen Behandlung der Ausnahmefachwerke lösen sich entsprechend auf, wenn elastische Stäbe und finite Verschiebungen der Knoten angesetzt werden.

Ein Fachwerk heißt statisch bestimmt, wenn die Lager- und die Stabkräfte aus den Gleichgewichtsbedingungen der Statik bestimmbar sind. In einem ebenen Fachwerk mit k Knoten, s Stabkräften und r Lagerreaktionen ergeben die Gleichgewichtsbedingungen 2k Gleichungen für die s+r Unbekannten. Damit die Stab- und die Lagerkräfte ermittelt werden können, muss daher die notwendige Bedingung 2k=s+r erfüllt sein. Bei räumlichen Fachwerken gibt es drei Gleichgewichtsbedingungen an jedem Knoten, sodass 3k=s+r notwendig ist. Die genannten Abzählkriterien sind in Ausnahmefachwerken erfüllt, ohne dass sie statisch bestimmt sind. Die Abzählkriterien sind nicht hinreichend für statische Bestimmtheit.^[2]

Wird aus einem statisch bestimmten Fachwerk ein beliebiger Stab entfernt, entsteht ein Mechanismus.^[1]:215 Im eingangs benutzten Ausnahmefachwerk aus sieben Stäben könnte der Stab DE ohne den rechten Stab CD frei um das Lager E drehen. In einem Ausnahmefachwerk kann der Stab, der entfernt wurde, um einen Mechanismus herzustellen, nach seinem Wiedereinsetzen jedoch eine (infinitesimal) kleine Bewegung des Mechanismus nicht verhindern.^[1]:216

Wird die genannte merkliche Verschiebung bei den #Mechanismen durch eine Veränderliche dφ bemaßt, im Bild beispielsweise durch den Drehwinkel dφ des Stabs DE, so stellt sich im Ausnahmefachwerk in mindestens einem der Stäbe eine Längenänderung der Ordnung dφ² oder höher ein, siehe #Bekannte Ausnahmefachwerke. Bei kleinen Verschiebungen 0<dφ⪡1 ist dφ²⪡dφ und wird in der Theorie erster Ordnung vernachlässigt, was beim Ausnahmefachwerk zu Problemen führt.

Das in der Einleitung gezeigte System ist dadurch, dass die Knoten C, D und E kollinear sind, ein Ausnahmefachwerk. Die die Ausnahme herbeiführende Eigenschaft ist genauer, dass zwei Stäbe zwischen zwei Knoten in einem nicht weiter gestützten Gelenk verbunden sind, das auf der Verbindungslinie der beiden Knoten liegt. Der denkbar einfachste Ausnahmefall dieser Art ist im Bild dargestellt. In gerader Linie angeordnet können die beiden Stäbe nur horizontale Stabkräfte abtragen und haben der vertikalen Kraft nichts entgegenzusetzen. Nur wenn das mittlere Gelenk nicht mehr unmittelbar auf der Verbindungslinie der Festlager rechts und links liegt, ist dem Fachwerk ein Gleichgewicht möglich. Aus demselben Grund hängt ein horizontal gespanntes Seil unter Querlast immer etwas durch.

Wird in der xy-Ebene der Punkt A im Ursprung, C bei (x_C, y_C) und B auf der x-Achse bei 2x_C angesetzt, ergeben sich die Stabkräfte bei vertikaler äußerer Kraft F zu

${\displaystyle {\mathsf {S={\frac {\sqrt {x_{C}^{2}+y_{C}^{2}}}{2y_{C}}}F}}}$

Wenn C auf AB liegt (sodass y_C=0 ist), dann wächst S über alle Grenzen, was unphysikalisch ist. Stattdessen würde sich C in Kraftrichtung verschieben (nach y_C≷0) und die Längenänderung der Stäbe berechnete sich mit einem Taylorpolynom mit Termen bis vierter Ordnung in y_C zu

${\displaystyle {\mathsf {{\sqrt {x_{C}^{2}+y_{C}^{2}}}-x_{C}={\frac {y_{C}^{2}}{2x_{C}}}-{\frac {y_{C}^{4}}{8x_{C}^{3}}}\dots }}}$

Diese Längenänderung zweiter und höherer Ordnung wird in der Theorie erster Ordnung vernachlässigt, weswegen hier auch eine elastische Dehnung der Stäbe nicht zur Lösung des Problems führt.

Erst eine Theorie höherer Ordnung vermag ein Gleichgewicht nach Verformung darzustellen. Die Ausgangslänge der Stäbe ist l₀=x_C und ${\displaystyle {\mathsf {l={\sqrt {x_{C}^{2}+y_{C}^{2}}}}}}$ ist die Länge der gedehnten. Dann sind die Stabkräfte S nach Dehnung um ε mit der Dehnsteifigkeit EA der Stäbe:

${\displaystyle {\begin{aligned}{\mathsf {\varepsilon }}:=&{\mathsf {{\frac {l-l_{0}}{l_{0}}}={\frac {{\sqrt {x_{C}^{2}+y_{C}^{2}}}-x_{C}}{x_{C}}}}}\\{\mathsf {S}}=&{\mathsf {EA\varepsilon =EA{\frac {{\sqrt {x_{C}^{2}+y_{C}^{2}}}-x_{C}}{x_{C}}}{\stackrel {\displaystyle !}{=}}{\frac {\sqrt {x_{C}^{2}+y_{C}^{2}}}{2y_{C}}}F}}\end{aligned}}}$

Daraus lässt sich eine Gleichung vierten Grades für die Stablänge l ableiten, aus deren Wert sich y_C ergibt.

Ein ebener Stabverband von zwei Dreiecken (blau in den Bildern), die durch drei Stäbe (lila) verbunden sind, ist im allgemeinen ein stabiles Fachwerk. Wenn jedoch die Verbindungsstäbe so liegen, dass ihre Richtungslinien entweder parallel zu einander sind oder sich in einem Punkt schneiden, wie in den Bildern unten, tritt der Ausnahmefall ein.^[1]:212

• 
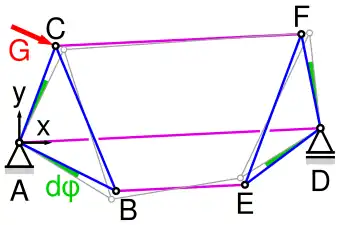  Ausnahmefachwerk aus zwei Dreiecken, die mit parallelen Stäben verbundenen sind
• 
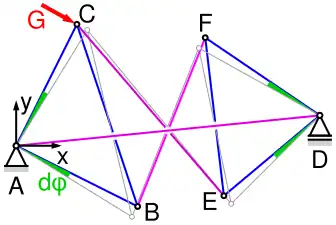  Ausnahmefachwerk aus zwei Dreiecken, die mit kreuzenden Stäben verbundenen sind

Bei parallelen Verbingungen lässt sich das einsehen, wenn die Dreiecke, wie im Bild angedeutet, als starr angesehen werden und sich gleichsinnig um A bzw. D mit dem (infinitesimal) kleinen Winkel dφ drehen. Die Knoten werden in der xy-Ebene mit x- und y-Koordinaten identifiziert, beispielsweise D=(x_D,y_D), und A in den Ursprung gelegt: A=(0,0). Dann berechnet sich mit dem Sinus und Cosinus sin bzw. cos:

${\displaystyle {\begin{aligned}{\mathsf {|BE|(d\varphi )}}=&{\Big (}{\mathsf {{\big (}(y_{B}-y_{E}+y_{D})\sin(d\varphi )+(x_{B}-x_{E}+x_{D})\cos(d\varphi )-x_{D}{\big )}^{2}}}\\&\dots +{\mathsf {{\big (}(y_{B}-y_{E}+y_{D})\cos(d\varphi )+(x_{E}-x_{B}-x_{D})\sin(d\varphi )-y_{D}{\big )}^{2}}}{\Big )}^{\frac {1}{2}}\\=&{\mathsf {|BE|(0)+\left[{\frac {y_{D}}{x_{D}}}-{\frac {y_{E}-y_{B}}{x_{E}-x_{B}}}\right]{\frac {(x_{B}-x_{E})x_{D}}{|BE|(0)}}d\varphi }}+{\mathcal {O}}({\mathsf {d}}\varphi ^{2})\end{aligned}}}$

wo das Landau-Symbol 𝓞(dφ²) Terme zusammenfasst, die dφ in mindestens zweiter Ordnung enthalten und die in der Theorie erster Ordnung vernachlässigt werden. Hier wurde das erste Taylorpolynom

${\displaystyle {\begin{aligned}{\mathsf {g(x)}}=&{\mathsf {\sqrt {{\big (}a\cos(x)+b\sin(x)+c{\big )}^{2}+{\big (}d\cos(x)+e\sin(x)+f{\big )}^{2}}}}\\=&{\mathsf {g(0)+{\frac {(a+c)b+(d+f)e}{g(0)}}x+{\mathcal {O}}(x^{2})}}\end{aligned}}}$

benutzt. Der Ausdruck in den eckigen Klammern […] oben verschwindet, wenn BE parallel zu AD ist, und entsprechendes leitet sich für |CF|(dφ) her. Wenn AD, BE und CF parallel sind, tritt der Ausnahmefall ein. Dasselbe leitet sich aus dem Kräftegleichgewicht an den Knoten A, B, C, E und demjenigen in x-Richtung am Knoten D her, denn unter den genannten Bedingungen wird die Matrix des Gleichungssystems singulär. Die aufwändigen Rechnungen für den Nachweis können von einem Computeralgebrasystem wie WxMaxima problemlos durchgeführt werden.

Bei sich kreuzenden Verbindungsstäben drehen sich die Dreiecke gegensinnig und es berechnet sich

${\displaystyle {\begin{aligned}{\mathsf {|BF|(d\varphi )}}=&{\Big (}{\mathsf {{\big (}(x_{B}-x_{F}+x_{D})\cos(d\varphi )+(y_{B}+y_{F}-y_{D})\sin(d\varphi )-x_{D}{\big )}^{2}}}\\&{\mathsf {\dots +{\big (}(y_{B}-y_{F}+y_{D})\cos(d\varphi )-(x_{B}+x_{F}-x_{D})\sin(d\varphi )-y_{D}{\big )}^{2}}}{\Big )}^{\frac {1}{2}}\\=&{\mathsf {|BF|(0)+2\left[m_{BF}{\frac {x_{D}}{2}}+n_{BF}-{\frac {y_{D}}{2}}\right]{\frac {x_{B}-x_{F}}{|BF|(0)}}d\varphi }}+{\mathcal {O}}({\mathsf {d}}\varphi ^{2})\end{aligned}}}$

Darin sind m_BF und n_BF die Steigung bzw. der y-Achsenabschnitt der Geraden BF. Der Term in der eckigen Klammer verschwindet, wenn sich AD und BF in der Mitte von AD schneiden. Entsprechendes leitet sich für |CE|(dφ) her. Wenn sich AD, BF und CE in der Mitte von AD schneiden, wie im rechten Bild, tritt der Ausnahmefall ein. Wiederum leitet sich dasselbe aus den Kräftegleichgewicht an den Knoten A, B, C, E und demjenigen in x-Richtung am Knoten D her, weil die Matrix des Gleichungssystems unter den genannten Bedingungen singulär wird.

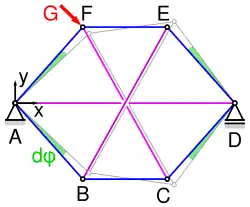
Ein Stabverband aus 9 Stäben, von denen 6 die Umfangsseiten eines Sechsecks (blau im Bild) und die anderen drei dessen Hauptdiagonalen sind (lila), bildet unter gewöhnlichen Umständen ein widerstandsfähiges Fachwerk. Sobald aber die Ecken des Sechsecks wie im Bild auf einem Kegelschnitt liegen, bildet der Stabverband ein Ausnahmefachwerk.^[1]:212

Die Strecken AB, AF, DE und CD werden wie im Bild angedeutet als starr angesehen und drehen sich um A bzw. D mit dem (infinitesimal) kleinen Winkel dφ. Dann berechnet sich

${\displaystyle {\begin{aligned}{\mathsf {|BC|(d\varphi )}}=&{\sqrt {\mathsf {|BC|(0)^{2}+2\,{\big (}(y_{B}-y_{C})\sin(d\varphi )+(1-\cos(d\varphi ))\,(x_{B}-x_{C}+x_{D}){\big )}\,x_{D}}}}\\=&{\mathsf {|BC|(0)+{\frac {[y_{B}-y_{C}]\,x_{D}}{|BC|(0)}}\,d\varphi +{\mathcal {O}}(d\varphi ^{2})}}\\{\mathsf {|EF|(d\varphi )}}=&{\mathsf {\sqrt {|EF|(0)^{2}+2\,{\big (}(y_{E}-y_{F})\sin(d\varphi )+(1-\cos(d\varphi ))\,(x_{F}-x_{E}+x_{D}){\big )}\,x_{D}}}}\\=&{\mathsf {|EF|(0)+{\frac {[y_{E}-y_{F}]\,x_{D}}{|EF|(0)}}\,d\varphi +{\mathcal {O}}(d\varphi ^{2})}}\\{\mathsf {|BE|(d\varphi )}}=&{\bigg (}{\mathsf {|BE|(0)^{2}+4\,{\Big (}{\big (}(x_{E}-x_{D})\,x_{B}+y_{B}\,y_{E}{\big )}\sin(d\varphi )}}\\&\quad {\mathsf {\dots +{\big (}(x_{E}-x_{D})\,y_{B}-x_{B}\,y_{E}{\big )}\,\cos(d\varphi ){\Big )}\sin(d\varphi )}}\\&\quad {\mathsf {\dots +2{\Big (}(y_{E}+y_{B})\sin(d\varphi ){\big (}1-\cos(d\varphi ){\big )}\,(x_{B}-x_{E}+x_{D}){\Big )}x_{D}}}{\bigg )}^{\frac {1}{2}}\\=&{\mathsf {|BE|(0)+\left[{\frac {y_{E}}{x_{E}-{\frac {x_{D}}{2}}}}-{\frac {y_{B}}{x_{B}-{\frac {x_{D}}{2}}}}\right]\,{\frac {(2\,x_{E}-x_{D})\,(x_{D}-2\,x_{B})}{2\,|BE|(0)}}\,d\varphi +{\mathcal {O}}(d\varphi ^{2})}}\\{\mathsf {|CF|(d\varphi )}}=&{\bigg (}{\mathsf {|CF|(0)^{2}+4{\Big (}{\big (}y_{C}\,y_{F}+(x_{C}-x_{D})\,x_{F}{\big )}\sin(d\varphi )}}\\&\quad {\mathsf {\dots +{\big (}x_{F}\,y_{C}+(x_{D}-x_{C})\,y_{F}{\big )}\,\cos(d\varphi ){\Big )}\sin(d\varphi )}}\\&\quad {\mathsf {\dots +2{\Big (}(x_{F}-x_{C}+x_{D})\,{\big (}1-\cos(d\varphi ){\big )}-(y_{C}+y_{F})\sin(d\varphi ){\Big )}x_{D}}}{\bigg )}^{\frac {1}{2}}\\=&{\mathsf {|CF|(0)+\left[{\frac {y_{F}}{x_{F}-{\frac {x_{D}}{2}}}}-{\frac {y_{C}}{x_{C}-{\frac {x_{D}}{2}}}}\right]{\frac {(2\,x_{F}-x_{D})\,(x_{D}-2\,x_{C})}{2\,|CF|(0)}}\,d\varphi +{\mathcal {O}}(d\varphi ^{2})}}\end{aligned}}}$

Die Terme erster Ordnung in dφ verschwinden, wenn

• y_B=y_C,
• y_E=y_F,
• AD mittig von BE geschnitten wird und
• AD mittig von CF geschnitten wird (siehe Terme in den eckigen Klammern),

und der Ausnahmefall tritt ein. Das ergibt sich auch aus dem Kräftegleichgewicht an den Knoten A, B, C, D und demjenigen in x-Richtung am Knoten E, denn unter den genannten Bedingungen wird die Matrix des Gleichungssystems singulär.

Commons: Ausnahmefachwerke – Sammlung von Bildern, Videos und Audiodateien

1. ↑ ^{a b c d e f g} A. Föppl: Die Lösung der Spannungsaufgabe für das Ausnahmefachwerk. In: Königlich Bayerische Akademie der Wissenschaften (Hrsg.): Sitzungsberichte. Band 1915, Nr. 9. Verlag der Königlich Bayerischen Akademie der Wissenschaften, München 1. Mai 1915, S. 211–229 (badw.de). 
2. ↑ ^{a b c d} D. Gross, W. Hauger, J. Schröder, W. A. Wall: Technische Mechanik 1. Statik. Springer-Verlag, Heidelberg 2011, ISBN 978-3-642-13805-8, S. 12,149–151, doi:10.1007/978-3-642-13806-5.