Attosekundenphysik

Die Attosekundenphysik, auch Attophysik oder allgemein Attosekundenwissenschaft genannt, ist ein Teilgebiet der Physik, das sich mit Phänomenen der Licht-Materie-Wechselwirkung beschäftigt, wobei Attosekundenpulse (10⁻¹⁸ s) von Photonen verwendet werden, um dynamische Prozesse in der Materie mit zuvor unerreichter Zeitauflösung zu analysieren. Die Attosekundenphysik hat eine sehr hohe zeitliche und räumliche Auflösung und erlaubt die Beobachtung ultraschneller Prozesse der Natur. In der Zeitdauer 10⁻¹⁸ s ordnen sich Elektronen innerhalb von Atomen neu an, in dieser Zeit formen sich chemische Bindungen oder brechen. Die Attosekundenphysik fungiert im übertragenen Sinn wie ein Mikroskop für die Zeit und erhöht das Verständnis der Quantenwelt.

In der Attosekundenphysik werden hauptsächlich spektroskopische Anrege-Abfrage-Methoden (englisch pump-probe experiment) eingesetzt, um den jeweiligen physikalischen Prozess zu untersuchen.^[1] Aufgrund der Komplexität dieses Forschungsgebietes ist für die Interpretation der Daten aus Attosekunden-Experimenten in der Regel ein enges Zusammenspiel zwischen modernsten experimentellen Aufbauten und fortgeschrittenen theoretischen Werkzeugen erforderlich.^[2]

Methodisch basiert alles auf der Erzeugung hoher Harmonischer (HHG, englisch high harmonic generation). Diese entstehen, wenn extrem intensives Laserlicht auf Atome trifft: Die Elektronen in den Atomen werden für einen winzigen Moment herausgerissen, vom Lichtfeld beschleunigt und dann wieder zurück ins Atom geschleudert. Dabei geben die Atome ultrakurze Lichtimpulse ab – das sind die sogenannten hohen Harmonischen.

Diese Lichtblitze sind besonders energiereich. Ihre Frequenz ist ein ungerades Vielfaches der ursprünglichen Laserfrequenz und reicht bis in den ultravioletten, extrem ultravioletten (EUV) (XUV, englisch extreme ultra violet) oder sogar den Röntgenbereich. Weil diese Pulse extrem kurz sind – oft nur wenige Attosekunden lang –, werden sie auch Attosekunden-Lichtblitze genannt. Es handelt sich um kohärente, extrem kurze EUV-Blitze, die als Stoppuhr in der quantendynamischen Welt fungieren.^[3] Durch geeignete Filterung lassen sich einzelne Attosekunden-Lichtblitze erzeugen.

Die Hauptinteressen der Attosekundenphysik sind:

1. Atomphysik: Untersuchung von Elektronenkorrelationseffekten, Photoemissionsverzögerungen und Ionisationstunneln.^[4]
2. Molekülphysik und Molekülchemie: Rolle der Elektronenbewegung in angeregten molekularen Zuständen durch Elektronentransfer, lichtinduzierte Photofragmentierung und lichtinduzierte Elektronentransferprozesse.^[5]
3. Festkörperphysik: Untersuchung der Exziton-Dynamik in fortgeschrittenen 2D-Materialien, Petahertz-Ladungsträgerbewegung in Festkörpern und Spin-Dynamik in ferromagnetischen Materialien.^[6]

Die Attosekundenphysik verfolgt das Ziel, die Bewegung von Elektronen in Atomen, Molekülen und Festkörpern mit bislang unerreichter zeitlicher Auflösung sichtbar zu machen. Eine der langfristigen Perspektiven dieser Forschung ist die gezielte Kontrolle elektronischer Dynamik in Echtzeit – ein entscheidender Schritt hin zu einer aktiven Steuerung quantenmechanischer Prozesse in der Materie.^[7]

Die Entwicklung der Attosekundenphysik wurde durch eine Reihe bahnbrechender Fortschritte in der Lasertechnologie ermöglicht: die Einführung breitbandig abstimmbarer Titan:Saphir-Laser (Ti:Sa) im Jahr 1986,^[8] die Technik der gechirpten Pulsverstärkung (CPA, englisch Chirped Pulse Amplification${\displaystyle \,}$) im Jahr 1988,^[9] die spektrale Verbreiterung hochenergetischer Femtosekundenpulse^[10] – beispielsweise durch Selbstphasenmodulation in gasgefüllten Hohlfasern (1996), die Einführung dispersionskompensierender Spiegeltechnologien (chirped mirrors) im Jahr 1994,^[11] sowie die Stabilisierung des Trägerhüllen-Offsets (englisch carrier-envelope phase stabilization${\displaystyle \,}$) ab dem Jahr 2000.^[12] Diese Entwicklungen führten ab 2004 zur Erzeugung isolierter Attosekunden-Lichtimpulse – generiert durch die Erzeugung hoher Harmonischer in Edelgasen als nichtlinearer Prozess^[13][14] und markierten den Beginn des eigenständigen Forschungsfeldes der Attosekundenphysik.^[15]

Der derzeitige Weltrekord für den kürzesten von Menschen erzeugten Lichtpuls liegt bei 43 Attosekunden.^[16]

Im Jahr 2022 erhielten Anne L'Huillier, Paul Corkum und Ferenc Krausz den Wolf-Preis für Physik für ihre bahnbrechenden Beiträge zur ultraschnellen Laserwissenschaft und Attosekundenphysik. Es folgte der Nobelpreis für Physik 2023, mit dem L'Huillier, Krausz und Pierre Agostini für ihre experimentellen Methoden zur Erzeugung von Attosekunden-Lichtblitzen zur Erforschung der Elektronendynamik in Materie ausgezeichnet wurden.

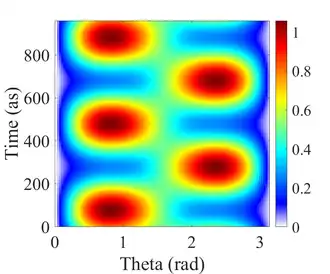
Für ein Quantenteilchen, das sich in einer Überlagerung aus dem Grundzustand ${\displaystyle |0\rangle }$ mit Energie ${\displaystyle \epsilon _{0}}$ und dem ersten ersten angeregten Zustand ${\displaystyle |1\rangle }$ mit der Energie ${\displaystyle \epsilon _{1}}$ befindet, lässt sich die zeitabhängige Wellenfunktion des Zweiniveausystems allgemein schreiben als^[17]:

${\displaystyle |\Psi (t)\rangle =c_{0}\,e^{-i\epsilon _{0}t/\hbar }|0\rangle +c_{1}\,e^{-i\epsilon _{1}t/\hbar }|1\rangle .}$

Die komplexen Koeffizienten ${\displaystyle c_{0}}$ und ${\displaystyle c_{1}}$ bestimmen die Wahrscheinlichkeitsamplituden für das Teilchen im jeweiligen Zustand. Gemäß der Bornschen Regel ergibt sich die Wahrscheinlichkeit für eine Messung in einem der Zustände als:

${\displaystyle |c_{0}|^{2}\quad {\text{bzw.}}\quad |c_{1}|^{2}}$

Die Wellenfunktion ist normiert, daher gilt die Bedingung:

${\displaystyle |c_{0}|^{2}+|c_{1}|^{2}=1}$

Der Erwartungswert eines selbstadjungierten Operators^[18] ${\displaystyle {\hat {P}}}$, der eine messbare physikalische Größe (Observable) beschreibt, ergibt sich aus:

${\displaystyle P(t)=\langle \Psi (t)|{\hat {P}}|\Psi (t)\rangle }$

Für ein Quantensystem, das sich in einer Überlagerung aus Grund- und erstem angeregtem Zustand befindet, ergibt sich der Erwartungswert der Observable zu:

${\displaystyle P(t)=|c_{0}|^{2}\langle 0|{\hat {P}}|0\rangle +|c_{1}|^{2}\langle 1|{\hat {P}}|1\rangle +2\,\mathrm {Re} \left(c_{1}^{*}c_{0}\langle 1|{\hat {P}}|0\rangle \,e^{i(\epsilon _{1}-\epsilon _{0})t/\hbar }\right)}$

Im Fall reeller Koeffizienten vereinfacht sich dieser Ausdruck zu:

${\displaystyle P(t)=|c_{0}|^{2}\langle 0|{\hat {P}}|0\rangle +|c_{1}|^{2}\langle 1|{\hat {P}}|1\rangle +2c_{1}c_{0}\langle 0|{\hat {P}}|1\rangle \cos \left({\frac {\epsilon _{1}-\epsilon _{0}}{\hbar }}t\right)}$

Die ersten beiden Terme sind zeitunabhängig. Der dritte Term beschreibt eine zeitlich oszillierende Komponente, die aus der Interferenz der Zustände resultiert. Die Schwingungsfrequenz der Erwartungswertdynamik beträgt:

${\displaystyle \omega ={\frac {\epsilon _{1}-\epsilon _{0}}{\hbar }}}$

Die zugehörige Periodendauer lautet:

${\displaystyle T_{c}={\frac {2\pi \hbar }{\epsilon _{1}-\epsilon _{0}}}}$

Für typische elektronische Übergänge mit Energiedifferenzen von etwa ${\displaystyle \epsilon _{1}-\epsilon _{0}\approx }$ 10 eV ergibt sich eine charakteristische Zeit^[7]:

${\displaystyle T_{c}\approx 400\,{\text{Attosekunden}}}$

Diese Zeitspanne bestimmt die typische Dynamik beobachtbarer physikalischer Größen bei elektronischen Übergängen in Atomen und Molekülen.

Um die zeitliche Entwicklung einer physikalischen Größe ${\displaystyle P(t)}$ mit hoher Auflösung zu untersuchen, ist ein kontrollierbarer Messprozess erforderlich, dessen charakteristische Zeitdauer kürzer ist als die zu erfassende Dynamik. Attosekunden-Lichtimpulse erfüllen diese Anforderung und ermöglichen die zeitaufgelöste Untersuchung ultrakurzer Prozesse im Bereich weniger Femtosekunden bis hinunter in den Attosekundenbereich. Sie dienen daher als zentrales Werkzeug zur Erforschung elektronischer Dynamik in Atomen, Molekülen und Festkörpern mit beispielloser zeitlicher Präzision^[19].

Um einen sich ausbreitenden Puls mit ultrakurzer Zeitdauer zu erzeugen, sind zwei Schlüsselelemente erforderlich: die Bandbreite und die zentrale Wellenlänge der elektromagnetischen Strahlung^[20]. Aus der Fourier-Analyse ergibt sich, dass die Zeitdauer eines Lichtpulses umso kürzer sein kann, je größer die verfügbare Bandbreite ist. Es gibt jedoch eine untere Grenze für die Mindestdauer, die für eine bestimmte zentrale Wellenlänge des Pulses genutzt werden kann. Diese Grenze ist der optische Zyklus, also die Dauer einer vollständigen Oszillation des elektrischen Feldes einer monochromatischen elektromagnetischen Welle^[21].

Für einen Puls im Niederfrequenzbereich, z. B. im Infrarotbereich (IR) bei einer Wellenlänge von ${\displaystyle \lambda ={\text{825 nm}}}$, beträgt die minimale Dauer etwa ${\displaystyle t_{\text{Puls}}=\lambda /c={\text{2,75}}\cdot 10^{-15}{\text{ s}}={\text{2,75 fs}}}$, wobei ${\displaystyle c}$ die Lichtgeschwindigkeit im Vakuum ist. Für ein Lichtfeld mit Zentralwellenlänge im Bereich der extrem ultravioletten Strahlung (EUV) bei ${\displaystyle \lambda ={\text{30 nm}}}$ beträgt die minimale Dauer dagegen etwa ${\displaystyle t_{\text{Puls}}={\text{100}}\cdot 10^{-18}{\text{ s}}={\text{100 as}}}$^[21].

Eine kürzere Zeitspanne erfordert daher die Verwendung kürzerer und energiereicherer Wellenlängen, sogar bis hinunter in den weichen Röntgenbereich unter 10 nm. Aus diesem Grund basieren die Standardtechniken zur Erzeugung von Attosekunden-Lichtblitzen auf Strahlungsquellen mit großer spektraler Bandbreite und zentraler Wellenlänge im EUV- bis Röntgenbereich^[22]. Die gebräuchlichsten Quellen, die diese Anforderungen erfüllen, sind Freie-Elektronen-Laser (FEL) und Anordnungen zur Erzeugung höherer Harmonischer (HHG).

Trifft ein hochenergetischer, stark fokussierter Femtosekundenlaserpuls (Wellenlänge 825 nm, Pulsbreite z. B. 5 fs, Intensität ${\displaystyle 4\cdot 10^{14}{\text{ W/cm}}^{2}}$) auf ein Edelgas (z. B. Neon), so entsteht ein Plateau aus hochfrequenten harmonischen Komponenten (z. B. ${\displaystyle N=11}$ zwischen der 41. und 61. Harmonischen). Es werden nur ungerade Harmonische beobachtet, was bei der Erzeugung von Harmonischen in einem isotropen, gasförmigen Medium mit Inversionssymmetrie zu erwarten ist. Der Modenabstand ist das Doppelte ${\displaystyle 2\omega _{L}}$ der Laserfrequenz ${\displaystyle \omega _{L}={\text{2,3}}\cdot 10^{15}{\text{ s}}^{-1}}$. Die Oberschwingungen im Plateaubereich sind nicht streng phasenstarr. Ihre zeitabhängige Ein-Atom-Emission besteht aus einer Folge ultrakurzer Pulse bei zwei Pulsen pro Halbzyklus. Diese entsprechen den beiden Hauptbahnen der Elektronen im Drei-Stufen-Rekollisionsmodell. Unter bestimmten geometrischen Bedingungen wird nur einer dieser Beiträge phasenangepasst, was zu einer Folge von Pulsen mit einem Puls pro Halbzyklus führt. Dabei entspricht die Pulslänge im Wesentlichen derjenigen, die man erhält, wenn alle Oberwellen die gleiche Phase und Amplitude haben. Betrachtet man nun ${\displaystyle N}$ Oberwellen mit gleicher Amplitude und Phase. Die Intensität ${\displaystyle I(t)}$ des von diesen Oberwellen ausgesandten Gesamtsignals lautet:^[23]

${\displaystyle I(t)\propto {\bigg |}\sum _{q=q_{0}}^{q=q_{0}+N-1}{\text{e}}^{-{\text{i}}(2q+1)\omega _{L}t}{\bigg |}^{2}={\frac {\sin ^{2}(N\omega _{L}t)}{\sin ^{2}(\omega _{L}t)}}}$

Die zeitabhängige Intensität ${\displaystyle I(t)}$ zeigt eine periodische Struktur mit der Halbperiode des Anregungslasers, also ${\displaystyle T_{L}/2=\pi /\omega _{L}}$, was für eine Wellenlänge von 825 nm etwa ${\displaystyle T_{L}/2={\text{1,37 fs}}}$ entspricht. Die Struktur besteht aus einer Sequenz scharfer Pulse mit einer zeitlichen Breite im Bereich von ${\displaystyle \Delta T\approx T_{L}/2N}$, was für N=11 etwa 125 as ergibt (volle Breite bei halbem Maximum, FWHM). Durch geeignete Filterung können einzelne Attosekundenpulse erzeugt werden. Diese Pulse sind kohärente, extrem kurze EUV-Blitze, die als Stoppuhr in der quantendynamischen Welt fungieren.

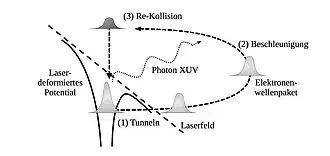
Das in Abbildung 5 dargestellte Rückstreu- oder Drei-Stufen-Modell zeigt, wie kurze Pulse im extremen Ultraviolett (englisch XUV${\displaystyle \,}$) mit einer Energie von etwa 10 bis 120 eV durch HHG erzeugt werden. Wird ein atomares Gas einem intensiven Laserfeld ausgesetzt, kann die Feldstärke das atomare Potential so stark deformieren, dass ein Elektron durch die entstehende Potentialbarriere tunneln kann. Das Elektron wird dann zunächst vom Atom weg beschleunigt und kann mit einer gewissen Wahrscheinlichkeit zurückkehren und rekombinieren. Im dritten Schritt, wenn das Elektron in die Kernposition zurückkehrt, wird bei der Rekombination gelegentlich eine Oberschwingung emittiert, deren Photonenenergie der Summe aus der kinetischen Energie des Elektrons und dem Ionisationspotential $I_p$ entspricht. Dieser kurze Lichtblitz liegt im extrem ultravioletten Spektralbereich. Seine Länge liegt im Attosekundenbereich und ist somit kürzer als die Periode des erzeugenden Laserfeldes. Dieser Prozess wiederholt sich für jeden Halbzyklus des erzeugenden Feldes. Die beobachteten hohen Harmonischen entstehen durch spektrale Interferenz der Attosekundenpulse aufeinanderfolgender Halbzyklen.

Viele Eigenschaften der HHG lassen sich intuitiv und sogar quantitativ durch das semiklassische Drei-Stufen-Modell (siehe Abbildung 5) erklären. In diesem Modell wird die Ausbreitung des Elektrons klassisch behandelt, während die Ionisation und die Rekombination quantenmechanisch sind.

Die Bewegung eines Elektrons in einem elektrischen Feld ${\displaystyle E_{z}(t)=E_{0}\cos(\omega _{L}t)}$ beschreibt das zweite Newtonsche Gesetz: Die Kraft, die auf einen Körper wirkt, ist gleich der zeitlichen Änderung seines Impulses ${\displaystyle p=mv}$. Bei konstanter Masse ${\displaystyle m}$ bewirkt die Kraft ${\displaystyle F}$ demnach die Beschleunigung ${\displaystyle a={\ddot {z}}(t)}$ des Elektrons. Die Kraft, die das Elektron im elektrischen Feld erfährt, ist gegeben durch ${\displaystyle F=-eE_{z}}$, wobei ${\displaystyle -e}$ die Ladung des Elektrons ist. Kombinieren wir diese Gleichungen, so erhalten wir:

${\displaystyle ma=m{\ddot {z}}(t)=-eE_{z}(t)=-eE_{0}\cos(\omega _{L}t)}$

mit den Anfangsbedingungen ${\displaystyle z(t_{i})=0}$ und ${\displaystyle {\dot {z}}(t_{i})=0}$ für ${\displaystyle t=t_{i}}$. Dies ist die Differentialgleichung, die die Bewegung eines freien Elektrons in einem oszillierenden elektrischen Feld ${\displaystyle E_{z}(t)}$ beschreibt. Ihre Lösung ergibt die Position des Elektrons ${\displaystyle z(t)}$ als Funktion der Zeit.

${\displaystyle z(t)=\textstyle {\frac {eE_{0}}{m\omega _{L}^{2}}}\left[\cos(\omega _{L}t)-\cos(\omega _{L}t_{i})+\omega _{L}(t-t_{i})\sin(\omega _{L}t_{i})\right]}$

Die kinetische Energie ${\displaystyle E_{\text{kin}}(t)=\textstyle {\frac {m}{2}}{\dot {z}}^{2}}$ beträgt

${\displaystyle E_{\text{kin}}(t)=\textstyle {\frac {m}{2}}\left({\frac {eE_{0}}{m\omega _{L}}}\right)^{2}[\sin(\omega _{L}t)-\sin(\omega _{L}t_{i})]^{2}=2U_{p}[\sin(\omega _{L}t)-\sin(\omega _{L}t_{i})]^{2}}$

mit der ponderomotorischen Energie ${\displaystyle U_{p}=\textstyle {\frac {e^{2}E_{0}^{2}}{4m\omega _{L}^{2}}}}$.

Die Zeit oder Phase der Rekombination, also ${\displaystyle t_{r}}$ oder ${\displaystyle \omega _{L}t_{r}}$ ist die Wurzel der Gleichung ${\displaystyle z(t_{r})=0}$. Die Energie des bei der Rekombination emittierten Photons ist dann gegeben durch ${\displaystyle E_{\text{kin}}(\omega _{L}t_{r})+I_{p}}$.

Für einen gegebenen Wert von ${\displaystyle E_{\text{kin}}}$ sind ${\displaystyle \omega _{L}t_{i}}$ und ${\displaystyle \omega _{L}t_{r}}$ die Lösungen der folgenden gekoppelten Gleichungen^[24]:

${\displaystyle {\begin{aligned}0&=\cos(\omega _{L}t_{r})-\cos(\omega _{L}t_{i})+(\omega _{L}t_{r}-\omega _{L}t_{i})\sin(\omega _{L}t_{i})\\\textstyle {\frac {E_{\text{kin}}}{2U_{p}}}&=[\sin(\omega _{L}t_{r})-\sin(\omega _{L}t_{i})]^{2}\end{aligned}}}$

mit den numerischen Lösungen von ${\displaystyle \omega _{L}t_{i}={\text{17°}}}$ und ${\displaystyle \omega _{L}t_{r}={\text{255°}}}$ zu diesen Anfangs- und Randbedingungen. Die kinetische Energie beträgt dann: ${\displaystyle E_{\text{kin}}(t)=2U_{p}[\sin(\omega _{L}t_{r})-\sin(\omega _{L}t_{i})]^{2}={\text{3,17}}\cdot U_{p}}$. Die maximale harmonische Photonenenergie ${\displaystyle E_{c}}$ ist gegeben durch das Grenzwertgesetz ${\displaystyle E_{c}=I_{p}+{\text{3,17}}\cdot U_{p}}$ mit dem Ionisationspotential des Zielatoms ${\displaystyle I_{p}}$ und der ponderomotorischen Energie ${\displaystyle U_{p}=e^{2}E_{0}^{2}/4m\omega _{L}^{2}}$. Dabei sind ${\displaystyle E_{0}}$ und ${\displaystyle \omega _{L}}$ die Stärke bzw. die Kreisfrequenz des antreibenden Feldes.

Sind (${\displaystyle \omega _{L}t_{i},\omega _{L}t_{r}}$) ein Paar der Lösungen, dann sind auch (${\displaystyle \omega _{L}t_{i}+n\pi ,\omega _{L}t_{r}+n\pi }$) ebenfalls Lösungen, wobei ${\displaystyle n}$ eine ganze Zahl ist. Bezeichnet man ${\displaystyle z(\omega _{L}t)}$ in Verbindung mit ${\displaystyle n}$ als ${\displaystyle z_{n}(\omega _{L}t)}$, so gilt ${\displaystyle z_{n}(\omega _{L}t)=(-1)^{n}z_{n=0}(\omega _{L}t-n\pi )}$. Das bedeutet, dass die Oberschwingungen in jedem Halbzyklus mit wechselnder Phase, d. h. mit wechselnder Feldrichtung abgestrahlt werden. Somit lässt sich das Oberschwingungsfeld ${\displaystyle E_{h}(\omega _{L}t)}$ wie folgt ausdrücken^[24]:

${\displaystyle E_{h}(\omega _{L}t)=\ldots +F_{h}(\omega _{L}t+2\pi )-F_{h}(\omega _{L}t+\pi )+F_{h}(\omega _{L}t)-F_{h}(\omega _{L}t-\pi )+F_{h}(\omega _{L}t-2\pi )-\ldots }$

Die Fourier-Transformierte dieser Gleichung nimmt nur für ungerade Vielfache von ${\displaystyle \omega _{L}}$ Werte ungleich Null an. Dieses Ergebnis erklärt, warum das harmonische Spektrum aus Komponenten ungerader Ordnung besteht.

Sobald eine Attosekunden-Lichtquelle verfügbar ist, kann der Puls auf die zu untersuchende Probe gerichtet werden, um seine Dynamik zu messen. Die am besten geeigneten experimentellen Beobachtungen zur Analyse der Elektronendynamik in Materie sind:

• Winkelasymmetrie in der Geschwindigkeitsverteilung der molekularen Bestandteile nach der Photoionisation^[25].
• Quantenausbeute molekularer Photofragmente^[26].
• Spektrum der transienten Absorption im EUV- bis Röntgenbereich^[27].
• Spektrum der transienten Reflektivität im EUV- bis Röntgenbereich^[28].
• Verteilung der kinetischen Energie des Photoelektrons^[4].
• Attosekunden-Elektronenmikroskopie^[29].

Die allgemeine Strategie besteht darin, eine Anrege-Abfrage-Technik der Ultrakurzzeit-Spektroskopie zu verwenden, um die ultraschnelle Dynamik im untersuchten Material mithilfe einer der oben genannten Messgrößen abzubilden^[2].

In einem typischen Anregungs-Abfrage-Experimentiergerät werden beispielsweise ein Attosekundenpuls im EUV- bis Röntgenbereich und ein intensiver Niederfrequenz-Infrarotpuls mit einer Leistung von ${\displaystyle 10^{11}-10^{14}{\text{ W/cm}}^{2}}$ und einer Dauer von wenigen zehn Femtosekunden parallel auf die untersuchte Probe fokussiert.

An diesem Punkt wird die gewünschte physikalische Beobachtung durch Variation der Verzögerung des Attosekundenpulses aufgezeichnet. Dieser übernimmt je nach Experiment die Anregung oder Abfrage. Der IR-Puls wiederum übernimmt die Abfrage oder Anregung^[30].

Die nächste Herausforderung besteht darin, die gesammelten Daten zu interpretieren, um grundlegende Informationen über die verborgene Dynamik und die Quantenprozesse in der Probe zu erhalten. Dies kann durch den Einsatz fortgeschrittener theoretischer Werkzeuge und numerischer Berechnungen erreicht werden^[31][32].

Mithilfe dieses experimentellen Schemas können verschiedene Arten von Dynamik in Atomen, Molekülen und Festkörpern untersucht werden. Dazu zählen beispielsweise lichtinduzierte Dynamik und angeregte Nichtgleichgewichtszustände. Dabei wird eine Zeitauflösung von Attosekunden erzielt^[25][26][28].

In der Attosekundenphysik werden typischerweise nichtrelativistisch gebundene Teilchen untersucht und elektromagnetische Felder mit mäßig hoher Intensität (${\displaystyle 10^{11}-10^{14}}$ W/cm²) verwendet^[33]. Dadurch ist es möglich, die Wechselwirkung von Licht und Materie im Rahmen der nichtrelativistischen und der semiklassischen Quantenmechanik zu diskutieren.

Die zeitliche Entwicklung einer einzelnen elektronischen Wellenfunktion ${\displaystyle |\psi (t)\rangle }$ in einem Atom wird durch die zeitabhängige Schrödingergleichung beschrieben^[34]:

${\displaystyle {\hat {H}}|\psi (t)\rangle ={\text{i}}\hbar {\frac {\partial \,\,\,}{\partial t}}|\psi (t)\rangle }$		(1.0)

mit dem Hamilton-Operator ${\displaystyle {\hat {H}}}$ für ein Teilchen mit der Ladung ${\displaystyle q}$ in einem Coulomb-Potential ${\displaystyle V_{C}({\hat {\textbf {r}}})}$ der der betrachteten Atomsorte und einem Vektorpotential ${\displaystyle {\textbf {A}}({\hat {\textbf {r}}},t)}$:

${\displaystyle {\hat {H}}={\frac {1}{2m}}({\hat {\textbf {p}}}-q{\textbf {A}}({\hat {\textbf {r}}},t))^{2}+V_{C}({\hat {\textbf {r}}})}$

${\displaystyle {\hat {\textbf {p}}}}$ und ${\displaystyle {\hat {\textbf {r}}}}$ sind der Impuls- bzw. Positionsoperator.

Das Vektorpotential ${\displaystyle {\textbf {A}}({\hat {\textbf {r}}},t)}$ und das elektrische Potential ${\displaystyle \Phi ({\hat {\textbf {r}}},t)}$ beschreiben das elektrische Feld ${\displaystyle {\textbf {E}}({\hat {\textbf {r}}},t)=\textstyle -{\frac {\partial {\textbf {A}}}{\partial t}}-\nabla \Phi }$ und die magnetische Flussdichte ${\displaystyle {\textbf {B}}({\hat {\textbf {r}}},t)=\nabla \times {\textbf {A}}}$, wobei das Vektorpotential die homogene Wellengleichung^[35]

${\displaystyle \nabla ^{2}{\textbf {A}}-{\frac {1}{c^{2}}}{\frac {\partial ^{2}{\textbf {A}}}{\partial t^{2}}}=0}$

erfüllt durch die Lösung

${\displaystyle {\textbf {A}}({\hat {\textbf {r}}},t)={\textbf {A}}_{0}{\text{e}}^{{\text{i}}({\textbf {k}}\cdot {\hat {\textbf {r}}}-\omega t)}={\textbf {A}}_{0}{\text{e}}^{{\text{i}}{\textbf {k}}\cdot {\hat {\textbf {r}}}}{\text{e}}^{-{\text{i}}\omega t}}$

bei einer Dispersionsrelation von ${\displaystyle \omega =kc}$.

In der Dipolnäherung gilt: ${\displaystyle {\text{e}}^{{\text{i}}{\textbf {k}}\cdot {\hat {\textbf {r}}}}\approx 1+{\text{i}}{\textbf {k}}\cdot {\hat {\textbf {r}}}\approx 1}$. Bei ${\displaystyle {\textbf {k}}\cdot {\hat {\textbf {r}}}-\omega t\approx -\omega t}$ verschwindet die Ortsabhängigkeit des Vektorpotentials ${\displaystyle {\textbf {A}}={\textbf {A}}(t)}$. Damit ist für ${\displaystyle \Phi =0}$ auch das elektrische Feld ${\displaystyle {\textbf {E}}=\textstyle -{\frac {\partial {\textbf {A}}}{\partial t}}={\textbf {E}}(t)}$ nur noch zeitabhängig und die magnetische Flussdichte ${\displaystyle {\textbf {B}}=\nabla \times {\textbf {A}}=0}$ verschwindet. Mit der Längeneichung^[36] ${\displaystyle \chi =-{\hat {\textbf {r}}}\cdot {\textbf {A}}(t)}$ oder M. Göppert-Mayer-Eichung^[37] verschwindet das Vektorpotential ${\displaystyle {\textbf {A}}'={\textbf {A}}+\nabla \chi ={\textbf {A}}+\nabla (-{\hat {\textbf {r}}}\cdot {\textbf {A}}(t))={\textbf {A}}-{\textbf {A}}=0}$ und das elektrische Potential wird erweitert zu ${\displaystyle \textstyle \Phi '=\Phi -{\frac {\partial \chi }{\partial t}}=\Phi -{\frac {\partial (-{\hat {\textbf {r}}}\cdot {\textbf {A}}(t))}{\partial t}}=-{\hat {\textbf {r}}}\cdot {\textbf {E}}}$.

Die zeitliche Entwicklung der Wellenfunktion ${\displaystyle |\psi (t)\rangle }$ eines Elektrons mit der Ladung ${\displaystyle q=-e}$ in einem Atom wird durch die Schrödingergleichung (1.0) mit dem Hamilton-Operator ${\displaystyle {\hat {H}}}$ der Licht-Materie-Wechselwirkung beschrieben:

${\displaystyle {\hat {H}}={\frac {1}{2m}}({\hat {\textbf {p}}}+e{\textbf {A}}'(t))^{2}+V_{C}({\hat {\textbf {r}}})-e\Phi '}$

Dieser Hamilton-Operator ${\displaystyle {\hat {H}}}$ vereinfacht sich im Rahmen der Dipolnäherung und unter der Voraussetzung, dass ${\displaystyle {\textbf {A}}'=0}$ und ${\displaystyle \textstyle \Phi '=-{\hat {\textbf {r}}}\cdot {\textbf {E}}}$ in der Längeneichung gilt, zu^[38][39]:

${\displaystyle {\hat {H}}={\frac {1}{2m}}{\hat {\textbf {p}}}^{2}+V_{C}({\hat {\textbf {r}}})+e\,{\hat {\textbf {r}}}\cdot {\textbf {E}}(t)}$

Dabei bezeichnet ${\displaystyle {\textbf {E}}(t)}$ das gesamte elektrische Feld in der Umgebung des Atoms, das auf ein Elektron mit der Ladung ${\displaystyle e}$ und der Masse ${\displaystyle m}$ einwirkt.

Die formale Lösung der Schrödingergleichung wird durch den Propagatorformalismus bestimmt^[40][41]:

${\displaystyle |\psi (t)\rangle ={\text{e}}^{-{\frac {\text{i}}{\hbar }}\int _{t_{0}}^{t}{\hat {H}}dt'}|\psi (t_{0})\rangle }$		(1.1)

Dabei ist ${\displaystyle |\psi (t_{0})\rangle }$ die Wellenfunktion des Elektrons zum Zeitpunkt ${\displaystyle t=t_{0}}$. Für fast alle praktischen Zwecke ist diese exakte Lösung jedoch unbrauchbar. Die obige Lösung kann jedoch mithilfe der Dyson-Reihe auch wie folgt geschrieben werden^[36][41]:

${\displaystyle |\psi (t)\rangle =-{\frac {\text{i}}{\hbar }}\int _{t_{0}}^{t}dt'{\Big [}{\text{e}}^{-{\frac {\text{i}}{\hbar }}\int _{t'}^{t}{\hat {H}}(t'')dt''}{\hat {H}}_{I}(t'){\text{e}}^{-{\frac {\text{i}}{\hbar }}\int _{t_{0}}^{t'}{\hat {H}}_{0}(t'')dt''}|\psi (t_{0})\rangle {\Big ]}+{\text{e}}^{-{\frac {\text{i}}{\hbar }}\int _{t_{0}}^{t}{\hat {H}}_{0}(t'')dt''}|\psi (t_{0})\rangle }$		(1.2)

wobei

${\displaystyle {\hat {H}}_{0}={\frac {1}{2m}}{\hat {\textbf {p}}}^{2}+V_{C}}$

der ungestörte Hamilton-Operator ist und

${\displaystyle {\hat {H}}_{I}=e\,{\hat {\textbf {r}}}\cdot {\textbf {E}}(t)}$

der Wechselwirkungs-Hamilton-Operator. Die bisher als Gleichung (1.1) bezeichnete formale Lösung von Gleichung (1.0) kann nun in Gleichung (1.2) als Überlagerung verschiedener Quantenpfade (oder Quantenbahnen) betrachtet werden, von denen jeder eine eigene Wechselwirkungszeit ${\displaystyle t'}$ mit dem elektrischen Feld hat.

Mit anderen Worten - Jeder Pfad ist durch drei Schritte im Integral über ${\displaystyle t'}$ auf der rechten Seite von Gleichung (1.2) gekennzeichnet:

1. Eine anfängliche zeitliche Entwicklung durch den ungestörten Hamilton-Operator ${\displaystyle {\hat {H}}_{0}}$ ohne das elektromagnetische Feld.
2. Dann folgt ein Kick durch das elektromagnetische Feld mittels des Wechselwirkungs-Hamilton-Operators ${\displaystyle {\hat {H}}_{I}(t')}$, der das Elektron anregt. Dieses Ereignis tritt zu einem beliebigen Zeitpunkt ${\displaystyle t'}$ ein, der den Quantenweg eindeutig charakterisiert.
3. Eine endgültige Entwicklung, die sowohl durch das Feld als auch durch das Coulomb-Potential bestimmt wird und durch den gesamten Hamilton-Operator ${\displaystyle {\hat {H}}}$ gegeben ist.

Parallel dazu gibt es auch einen Quantenpfad, der das Feld überhaupt nicht wahrnimmt. Diese Trajektorie wird durch den zweiten Summanden auf der rechten Seite von Gleichung (1.2) bestimmt. Dieser Prozess ist vollständig zeitumkehrbar, d. h., er kann auch in umgekehrter Reihenfolge ablaufen^[41]. Die Gleichung (1.2) ist nicht einfach zu handhaben. Physiker verwenden sie jedoch als Grundlage für numerische Berechnungen, weiterführende Diskussionen oder verschiedene Näherungen^[36][42].

Bei Starkfeldwechselwirkungsproblemen, bei denen Ionisation auftreten kann, kann man sich vorstellen, Gleichung (1.2) in einen bestimmten Kontinuumszustand (unbeschränkter Zustand oder freier Zustand) ${\displaystyle |{\textbf {p}}\rangle }$ mit Impuls ${\displaystyle {\textbf {p}}}$ zu projizieren, für den gilt:

${\displaystyle c_{\textbf {p}}(t)=\langle {\textbf {p}}|\psi (t)\rangle =-{\frac {\text{i}}{\hbar }}\int _{t_{0}}^{t}dt'\langle {\textbf {p}}|{\text{e}}^{-{\frac {\text{i}}{\hbar }}\int _{t'}^{t}{\hat {H}}(t'')dt''}{\hat {H}}_{I}(t'){\text{e}}^{-{\frac {\text{i}}{\hbar }}\int _{t_{0}}^{t'}{\hat {H}}_{0}(t'')dt''}|{\psi (t_{0})}\rangle +\langle {\textbf {p}}|{\text{e}}^{-{\frac {\text{i}}{\hbar }}\int _{t_{0}}^{t}{\hat {H}}_{0}(t'')dt''}|\psi (t_{0})\rangle }$		(1.3)

Dabei ist ${\displaystyle |c_{\textbf {p}}(t)|^{2}}$ die Wahrscheinlichkeit, das Elektron zu einem bestimmten Zeitpunkt ${\displaystyle t}$ im Kontinuumszustand ${\displaystyle |{\textbf {p}}\rangle }$ zu finden. Ist diese Wahrscheinlichkeit größer als Null, ist das Elektron photoionisiert.

Bei der Mehrzahl der Anwendungen wird der zweite Summand der Gleichung (1.3) nicht berücksichtigt und nur der erste Term diskutiert^[36][41]:

${\displaystyle a_{\textbf {p}}(t)=-{\frac {\text{i}}{\hbar }}\int _{t_{0}}^{t}dt'\langle {\textbf {p}}|{\text{e}}^{-{\frac {\text{i}}{\hbar }}\int _{t'}^{t}{\hat {H}}(t'')dt''}{\hat {H}}_{I}(t'){\text{e}}^{-{\frac {\text{i}}{\hbar }}\int _{t_{0}}^{t'}{\hat {H}}_{0}(t'')dt''}|{\psi (t_{0})}\rangle }$		(1.4)

Die Amplitude in Gleichung (1.4) ist auch als zeitumgekehrte S-Matrix-Amplitude bekannt^[36] und gibt die Wahrscheinlichkeit der Photoionisation durch ein generisches zeitlich veränderliches elektrisches Feld an.

Die Starkfeldnäherung, auch Keldysh-Faisal-Reiss-Theorie genannt, ist ein physikalisches Modell, das 1964 vom russischen Physiker Keldysh aufgestellt wurde^[43]. Es wird derzeit zur Beschreibung des Verhaltens von Atomen (und Molekülen) in intensiven Laserfeldern verwendet.

Die Starkfeld-Approximation ist die Grundlage für die Diskussion über die Erzeugung höherer Harmonischer sowie über die Wechselwirkung bei der Attosekunden-Anregung mit Atomen.

Die Hauptannahme der Starkfeldnäherung ist, dass die Dynamik der freien Elektronen durch das Laserfeld dominiert wird und das Coulomb-Potential ${\displaystyle V_{C}\approx 0}$ als vernachlässigbare Störung betrachtet wird^[44]. Diese Annahme formt die Gleichung (1.4) um in:

${\displaystyle a_{\textbf {p}}^{SFN}(t)=-{\frac {\text{i}}{\hbar }}\int _{t_{0}}^{t}dt'\langle {\textbf {p}}|{\text{e}}^{-{\frac {\text{i}}{\hbar }}\int _{t'}^{t}{\hat {H}}_{V}(t'')dt''}{\hat {H}}_{I}(t'){\text{e}}^{-{\frac {\text{i}}{\hbar }}\int _{t_{0}}^{t'}{\hat {H}}_{0}(t'')dt''}|{\psi (t_{0})}\rangle }$		(1.5)

wobei ${\displaystyle {\hat {H}}_{V}={\textstyle {\frac {1}{2m}}}({\hat {\textbf {p}}}+e{\textbf {A}}(t))^{2}}$ der Volkov-Hamilton-Operator ist. Dieser wird hier der Einfachheit halber in der Geschwindigkeitseichung mit dem Vektorpotential ${\displaystyle {\textbf {A}}({\hat {\textbf {r}}},t)={\textbf {A}}(t)}$ und ${\displaystyle \nabla \cdot {\textbf {A}}=0}$ ausgedrückt

${\displaystyle {\hat {H}}_{V}={\frac {{\hat {\textbf {p}}}^{2}}{2m}}+{\frac {{\textbf {A}}(t)\cdot {\hat {\textbf {p}}}}{m}}+{\frac {e^{2}{\textbf {A}}(t))^{2}}{2m}}}$

mit dem elektrischen Feld ${\displaystyle \textstyle {\textbf {E}}(t)=-{\frac {\partial {\textbf {A}}(t)}{\partial t}}}$^[39][45].

Zur Vereinfachung der Diskussion wird ein Atom im Rahmen der Ein-Elektron-Näherung betrachtet, bei dem nur ein einziges diskretes Energieniveau mit der Ionisierungsenergie ${\displaystyle I_{P}}$ berücksichtigt wird. Der Zustand ${\displaystyle |0\rangle }$ ist dabei zu Beginn (bei ${\displaystyle t_{0}=-\infty }$) mit genau einem Elektron besetzt und repräsentiert den atomaren Grundzustand, von dem aus die zeitliche Entwicklung der Wellenfunktion startet:

${\displaystyle {\hat {H}}_{0}|0\rangle =-I_{P}|0\rangle }$ und ${\displaystyle |\psi (t)\rangle ={\text{e}}^{-{\frac {\text{i}}{\hbar }}\int _{-\infty }^{t'}{\hat {H}}_{0}dt}|0\rangle ={\text{e}}^{{\frac {\text{i}}{\hbar }}I_{P}t'}|0\rangle }$

Außerdem können wir die Kontinuumszustände ${\displaystyle \langle {\textbf {r}}|{\textbf {p}}\rangle =(2\pi )^{-{\frac {3}{2}}}{\text{e}}^{i{\textbf {p}}\cdot {\textbf {r}}/\hbar }}$ als ebene Wellen betrachten. Dies ist eine ziemlich vereinfachte Annahme. Vernünftiger wäre es gewesen die exakten Streuzustände der Atome als Kontinuumszustand zu verwenden^[46]. Die zeitliche Entwicklung von einfachen ebenen Wellen mit dem Volkov-Hamilton-Operator ist gegeben durch:

${\displaystyle \langle {\textbf {p}}|{\text{e}}^{-{\frac {\text{i}}{\hbar }}\int _{t'}^{t}{\hat {H}}_{V}(t'')dt''}=\langle {\textbf {p}}+e{\textbf {A}}(t)|{\text{e}}^{-{\frac {\text{i}}{\hbar }}\int _{t'}^{t}({\textbf {p}}+e{\textbf {A}}(t''))^{2}dt''/2m}}$

Aus Gründen der Konsistenz mit Gleichung (1.5) wurde die Entwicklung hier bereits korrekt in die Längeneichung umgerechnet^[47]. Daraus folgt, dass sich die endgültige Impulsverteilung eines einzelnen Elektrons in einem Ein-Niveau-Atom mit dem Ionisierungspotential ${\displaystyle I_{P}}$ wie folgt ausdrücken lässt:

${\displaystyle a_{\textbf {p}}(t)^{SFN}=-{\frac {\text{i}}{\hbar }}\int _{-\infty }^{t}{\textbf {E}}(t')\cdot {\textbf {d}}[{\textbf {p}}+e{\textbf {A}}(t')]{\text{e}}^{+{\frac {\text{i}}{\hbar }}(I_{P}t'-S(t,t'))}dt'}$		(1.6)

wobei

${\displaystyle {\textbf {d}}[{\textbf {p}}+e{\textbf {A}}(t')]=\langle {\textbf {p}}+e{\textbf {A}}(t')|e\,{\hat {\textbf {r}}}|0\rangle }$

der Dipol-Erwartungswert (oder Übergangsdipolmoment) ist und

${\displaystyle S(t,t')=\int _{t'}^{t}{\frac {1}{2m}}({\textbf {p}}+e{\textbf {A}}(t''))^{2}dt''}$

die semiklassische Wirkung.

Das Ergebnis von Gleichung (1.6) bildet die Grundlage für das Verständnis von Phänomenen wie:

• Der Prozess der Erzeugung hoher Harmonischer ist typischerweise das Ergebnis einer starken Feldwechselwirkung von Edelgasen mit einem intensiven niederfrequenten Impuls^[48].
• Attosekunden-Anrege-Abfrage-Experimente mit einfachen Atomen^[49].
• Die Debatte über die Dauer des Tunneleffekts^[50][51].

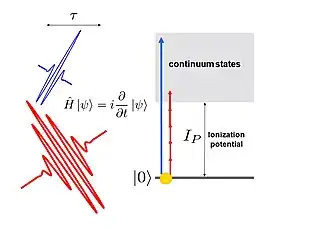
Attosekunden-Anrege-Abfrage-Experimente mit einfachen Atomen sind ein grundlegendes Instrument, um die Zeitdauer eines Attosekundenpulses zu messen^[52] und verschiedene Quanteneigenschaften der Materie zu erforschen^[49].

Im Rahmen der Starkfeldnäherung lassen sich diese Art von Experimenten leicht beschreiben, indem die Ergebnisse von Gleichung (1.6) genutzt werden, wie unten beschrieben.

Ein einfaches Modell beschreibt die Wechselwirkung zwischen einem einzelnen aktiven Elektron in einem Ein-Niveau-Atom und zwei Feldern: einem intensiven Femtosekunden-Infrarot-Puls (IR) mit der Feldstärke ${\displaystyle ({\textbf {E}}_{IR}(t)}$ und dem Vektorpotential ${\displaystyle {\textbf {A}}_{IR}(t)}$ sowie einem schwachen Attosekundenimpuls ${\displaystyle ({\textbf {E}}_{EUV}(t),{\textbf {A}}_{EUV}(t))}$, der im Extrem-Ultraviolett-Bereich (EUV) zentriert ist.

Wenn man diese Felder in (1.6) einsetzt, ergibt sich daraus

${\displaystyle a_{\textbf {p}}(t)=-{\frac {\text{i}}{\hbar }}\int _{-\infty }^{t}({\textbf {E}}_{EUV}(t')+{\textbf {E}}_{IR}(t'))\cdot {\textbf {d}}[{\textbf {p}}+e{\textbf {A}}_{EUV}(t')+e{\textbf {A}}_{IR}(t')]{\text{e}}^{+{\frac {\text{i}}{\hbar }}(I_{P}t'-S(t,t'))}dt'}$		(1.7)

mit

${\displaystyle S(t,t')=\int _{t'}^{t}{\frac {1}{2m}}({\textbf {p}}+e{\textbf {A}}_{IR}(t'')+e{\textbf {A}}_{EUV}(t''))^{2}dt''}$.

An dieser Stelle können wir die Gleichung (1.7) in die beiden Beiträge direkte Ionisation und Starkfeldionisation durch Multiphotonenabsorption aufteilen. In der Regel sind diese beiden Prozesse in verschiedenen energetischen Bereichen des Kontinuums von Bedeutung. Unter typischen Versuchsbedingungen wird daher der Multiphotonenprozess vernachlässigt und lediglich die direkte Ionisierung durch den Attosekundenpuls berücksichtigt^[36]. Da der Attosekundenimpuls schwächer ist als der Infrarotimpuls, gilt ${\displaystyle {\textbf {A}}_{IR}(t)\gg {\textbf {A}}_{EUV}(t)}$. Daher wird ${\displaystyle {\textbf {A}}_{EUV}(t)}$ in Gleichung (1.7) üblicherweise vernachlässigt. Darüber hinaus können wir den Attosekundenpuls als verzögerte Funktion in Bezug auf das IR-Feld umschreiben: ${\displaystyle [{\textbf {A}}_{IR}(t),{\textbf {E}}_{EUV}(t-\tau )]}$.

In einem Anrege-Abfrage-Experiment mit einem intensiven IR-Impuls und einem verzögerten EUV-Impuls von einer Attosekunde folgt die Wahrscheinlichkeitsverteilung ein ionisiertes Elektron mit einem Impuls ${\displaystyle {\textbf {p}}}$ im Kontinuum zu finden, der Wahrscheinlichkeitsverteilung ${\displaystyle |a_{\textbf {p}}(\tau )|^{2}}$:

${\displaystyle a_{\textbf {p}}(\tau )=-{\frac {\text{i}}{\hbar }}\int _{-\infty }^{\infty }{\textbf {E}}_{EUV}(t-\tau )\cdot {\textbf {d}}[{\textbf {p}}+e{\textbf {A}}_{IR}(t)]{\text{e}}^{+{\frac {\text{i}}{\hbar }}(I_{P}t-S(t))}dt}$		(1.8)

mit

${\displaystyle S(t)={\frac {1}{2m}}|{\textbf {p}}|^{2}t+\int _{t}^{\infty }\left({\frac {e{\textbf {A}}_{IR}(t')\cdot {\textbf {p}}}{m}}+{\frac {e^{2}|{\textbf {A}}_{IR}(t')|^{2}}{2m}}\right)dt'}$

Die Gleichung (1.8) beschreibt das Photoionisationsphänomen der Zweifarbenwechselwirkung (EUV-IR) mit einem Ein-Niveau-Atom und einem einzelnen aktiven Elektron. Dieses Ergebnis lässt sich als Quanteninterferenzprozess zwischen allen möglichen Ionisierungspfaden betrachten, der durch einen verzögerten EUV-Attosekundenpuls ausgelöst wird und anschließend in den Kontinuumszuständen weiterläuft, die durch ein starkes IR-Feld angetrieben werden^[36]. Die daraus resultierende zweidimensionale Photoelektronenverteilung (Impuls oder Energie vs. Verzögerung) wird als Attosekunden-Schmierbildkamera bezeichnet^[53].

Im Folgenden werden einige der gängigsten Techniken und Ansätze, die in Attosekunden-Forschungszentren verfolgt werden, aufgeführt und erörtert.

In der Attosekundenforschung stellt die Charakterisierung der zeitlichen Eigenschaften der Attosekundenpulse, die in allen Anrege-Abfrage-Experimenten mit Atomen, Molekülen oder Festkörpern zum Einsatz kommen, eine tägliche Herausforderung dar.

Die am häufigsten verwendete Technik basiert auf der frequenzaufgelösten optischen Ansteuerung FROG-CRAB (FROG, englisch Frequency-Resolved Optical Gating) und dient der vollständigen Rekonstruktion von Attosekundenpulsen (CRAB, englisch Complete Reconstruction of Attosecond Bursts)^[52]. Die ursprünglich 1991 für die Charakterisierung von Pikosekunden- und Femtosekunden-Pulsen entwickelte FROG-Technik konnte auf das Attosekundengebiet übertragen werden^[55].

Die vollständige Rekonstruktion von Attosekundenlichtblitzen (CRAB) ist eine Erweiterung der FROG-Technik, bei der die dieselbe Idee für die Feldrekonstruktion genutzt wird. Mit anderen Worten: Bei FROG-CRAB wird ein Attosekundenpuls in ein Elektronenwellenpaket umgewandelt, das durch atomare Photoionisation im Kontinuum freigesetzt wird, wie in Gleichung (1.8) dargestellt. Die Aufgabe des niederfrequenten Laserpulses (des Infrarotpulses) besteht darin, die Zeitmessung auszulösen.

Untersucht man die verschiedenen Verzögerungen zwischen dem niederfrequenten und dem Attosekundenpuls, erhält man ein Schmierbild^[53]. Dieses zweidimensionale Spektrogramm wird später von einem Rekonstruktionsalgorithmus analysiert, um sowohl den Attosekundenpuls als auch den IR-Puls wiederzufinden, ohne dass Vorkenntnisse über einen der beiden erforderlich sind.

Wie Gleichung (1.8) jedoch aufzeigt, ist die eigentliche Grenze dieser Technik die Kenntnis der atomaren Dipoleigenschaften, insbesondere der Phase der atomaren Dipolmomente^[49][56].

In der Regel erfolgt die Rekonstruktion sowohl des niederfrequenten Feldes als auch des Attosekundenpulses aus einer Schmierbildaufnahme durch iterative Algorithmen. Beispiele hierfür sind:

• Algorithmus für verallgemeinerte Hauptkomponentenprojektionen (PCGPA, englisch Principal Component Generalized Projections Algorithm).^[57]
• Verallgemeinerter Volkov-Transformationsprojektionsalgorithmus (VTGPA, englisch Volkov Transform Generalized Projection Algorithm).^[58]
• Erweiterte ptychographische Iterationsmaschine (ePIE, englisch extended Ptychographic Iterative Engine).^[59]

• Kurzzeitphysik
• Femtochemie
• Femtosekundenlaser
• Ultrakurzpulslaser
• Chirped Pulse Amplification
• Freie-Elektronen-Laser
• Ultrakurzzeit-Spektroskopie

• Bucksbaum PH: Attophysics: Ultrafast control. In: Nature. 421. Jahrgang, Nr. 6923, Februar 2003, S. 593–4, doi:10.1038/421593a, PMID 12571581, bibcode:2003Natur.421..593B (englisch). 
• Thorsten Naeser: Ultraschneller Tauchgang in die Atome : Attosekunden-Blitze erkunden den Quantenkosmos. 1. Auflage. WILEY-VCH, Weinheim 2014, ISBN 978-3-527-41125-2, S. 312 - 313. 
• Cerullo G, Nisoli M: Ultrafast lasers: from femtoseconds to attoseconds. In: Europhysics News. 50. Jahrgang, Nr. 2, März 2019, S. 11–4, doi:10.1051/epn/2019201, bibcode:2019ENews..50b..11C (englisch). 
• Kennedy S, Burdick A: Stopping Time: What can you do in a billionth of a billionth of a second? Juni 2003; abgerufen im 1. Januar 1 (englisch). 
• Nisoli M: The Birth of Attochemistry. In: Optics and Photonics News. 30. Jahrgang, Nr. 7, Juli 2019, S. 32–9, doi:10.1364/OPN.30.7.000032, bibcode:2019OptPN..30...32N (englisch).