Allgemeine Koordinatenform

Die allgemeine Koordinatenform (kurz allgemeine Form^[1][2] oder Koordinatenform)^{[A 1]} ist in der Mathematik eine spezielle Form einer Geradengleichung oder Ebenengleichung. Bei der allgemeinen Form wird eine Gerade in der euklidischen Ebene oder eine Ebene im euklidischen Raum in Form einer linearen Gleichung beschrieben. Die Unbekannten der Gleichung sind dabei die Koordinaten der Punkte der Gerade oder Ebene in einem kartesischen Koordinatensystem. Die allgemeine Form ist damit eine spezielle implizite Darstellung der Gerade oder Ebene.

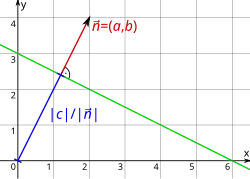
In der allgemeinen Koordinatenform wird jede Gerade in der Ebene durch drei reelle Zahlen ${\displaystyle a}$, ${\displaystyle b}$ und ${\displaystyle c}$ über eine lineare Gleichung beschrieben. Eine Gerade besteht dann aus denjenigen Punkten, deren Koordinaten ${\displaystyle (x,y)}$ die Gleichung

${\displaystyle ax+by=c}$

erfüllen.^[3] Hierbei muss ${\displaystyle a}$ oder ${\displaystyle b}$ ungleich null sein.

Bei den Zahlen ${\displaystyle a}$ und ${\displaystyle b}$ handelt es sich um die Komponenten des Normalenvektors ${\displaystyle {\vec {n}}=(a,b)}$ der Geraden. Der Abstand der Geraden vom Koordinatenursprung wird durch ${\displaystyle |c|/|{\vec {n}}|}$ angegeben. Ist der Normalenvektor normiert, also ein Einheitsvektor, dann beträgt der Abstand gerade ${\displaystyle |c|}$.

Die Gerade im Bild oben wird beschrieben durch die allgemeine Koordinatenform

${\displaystyle 1x+2y=6}$.

Jede Wahl von ${\displaystyle (x,y)}$, die diese Gleichung erfüllt, beispielsweise ${\displaystyle (0,3)}$ oder ${\displaystyle (4,1)}$, entspricht genau einem Geradenpunkt.

• Falls ${\displaystyle a=0}$ ist, verläuft die Gerade parallel zur ${\displaystyle x}$-Achse, und falls ${\displaystyle b=0}$ ist, parallel zur ${\displaystyle y}$-Achse.
• Falls ${\displaystyle c=0}$ ist, handelt es sich bei der Geraden um eine Ursprungsgerade.
• Falls ${\displaystyle c=1}$ ist, liegt die Geradengleichung in Achsenabschnittsform vor; die Achsenschnittpunkte sind dann ${\displaystyle (1/a,0)}$ und ${\displaystyle (0,1/b)}$.

Aus der Normalenform ${\displaystyle {\vec {x}}\cdot {\vec {n}}={\vec {p}}\cdot {\vec {n}}}$ einer Geraden mit Stützvektor ${\displaystyle {\vec {p}}=(p_{1},p_{2})^{T}}$ und Normalenvektor ${\displaystyle {\vec {n}}=(n_{1},n_{2})^{T}}$ erhält man durch Ausmultiplizieren die Gleichung

${\displaystyle n_{1}x+n_{2}y=p_{1}n_{1}+p_{2}n_{2}}$

Hierbei handelt es sich schon um die allgemeine Koordinatenform der Gerade mit ${\displaystyle a=n_{1},~b=n_{2},~c=p_{1}n_{1}+p_{2}n_{2}}$.

Liegt eine Gerade in hessescher Normalform vor, kann der Parameter ${\displaystyle c}$ auch von dort übernommen werden.

Aus der Parameterform einer Geradengleichung mit Stützvektor ${\displaystyle {\vec {p}}=(p_{1},p_{2})^{T}}$ und Richtungsvektor ${\displaystyle {\vec {u}}=(u_{1},u_{2})^{T}}$ wird zunächst ein Normalenvektor der Geraden über ${\displaystyle {\vec {n}}=(-u_{2},u_{1})}$ bestimmt und daraus dann die Parameter der allgemeinen Form als

${\displaystyle a=-u_{2},~b=u_{1},~c=-p_{1}u_{2}+p_{2}u_{1}}$.

Alternativ kann man die Koordinatenform herleiten, indem man den Parameter ${\displaystyle s}$ aus dem Gleichungssystem

${\displaystyle {\begin{matrix}x=p_{1}+su_{1}\ &({\text{I}})\\y=p_{2}+su_{2}\ &({\text{II}})\end{matrix}}}$

eliminiert. Dazu stellt man eine Koordinatengleichung, in der die Koordinate des Richtungsvektors nicht null ist,^{[A 2]} nach ${\displaystyle s}$ um und setzt dann den erhaltenen Term für ${\displaystyle s}$ in die andere Koordinatengleichung ein. Ist etwa ${\displaystyle u_{2}\neq 0}$, so folgt aus ${\displaystyle ({\text{II}})}$ die Beziehung ${\displaystyle s=(y-p_{2})/u_{2}}$, und durch Einsetzen in ${\displaystyle ({\text{I}})}$ wird ${\displaystyle s}$ eliminiert. Multipliziert man die parameterfreie Gleichung dann noch mit ${\displaystyle u_{2}}$ und löst nach null auf, so erhält man

${\displaystyle -u_{2}x+u_{1}y=-p_{1}u_{2}+p_{2}u_{1}}$.

Aus der Zweipunkteform einer Gerade durch die beiden Punkte ${\displaystyle (x_{1},y_{1})}$ und ${\displaystyle (x_{2},y_{2})}$ erhält man durch Ausmultiplizieren die Parameter der allgemeinen Form

${\displaystyle a=y_{1}-y_{2},b=x_{2}-x_{1},c=x_{2}y_{1}-x_{1}y_{2}}$.

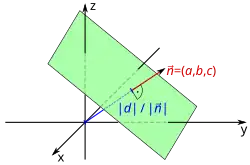
Analog wird eine Ebene im dreidimensionalen Raum in der allgemeinen Koordinatenform durch vier reelle Zahlen ${\displaystyle a}$, ${\displaystyle b}$, ${\displaystyle c}$ und ${\displaystyle d}$ beschrieben. Eine Ebene besteht dann aus denjenigen Punkten, deren Koordinaten ${\displaystyle (x,y,z)}$ die Gleichung

${\displaystyle ax+by+cz=d}$

erfüllen. Hierbei muss zumindest einer der Parameter ${\displaystyle a}$, ${\displaystyle b}$, ${\displaystyle c}$ ungleich null sein. Bei den Zahlen ${\displaystyle a}$, ${\displaystyle b}$ und ${\displaystyle c}$ handelt es sich um die Komponenten des Normalenvektors ${\displaystyle {\vec {n}}=(a,b,c)}$ der Ebene. Der Abstand der Ebene vom Koordinatenursprung wird durch ${\displaystyle |d|/|{\vec {n}}|}$ angegeben. Ist der Normalenvektor normiert, dann beträgt der Abstand gerade ${\displaystyle |d|}$.

Ein Beispiel für eine Ebenengleichung in allgemeiner Koordinatenform ist

${\displaystyle 2x+3y-z=1}$.

Jede Wahl von ${\displaystyle (x,y,z)}$, die diese Gleichung erfüllt, beispielsweise ${\displaystyle (1,0,1)}$ oder ${\displaystyle (0,1,2)}$, entspricht genau einem Ebenenpunkt.

• Falls ${\displaystyle a=0}$ ist, verläuft die Ebene parallel zur ${\displaystyle x}$-Achse, falls ${\displaystyle b=0}$ ist, parallel zur ${\displaystyle y}$-Achse, und falls ${\displaystyle c=0}$ ist, parallel zur ${\displaystyle z}$-Achse.
• Falls ${\displaystyle d=0}$ ist, handelt es sich bei der Ebene um eine Ursprungsebene.
• Falls ${\displaystyle d=1}$ ist, liegt die Ebenengleichung in Achsenabschnittsform vor; die Achsenschnittpunkte sind dann ${\displaystyle (1/a,0,0)}$, ${\displaystyle (0,1/b,0)}$ und ${\displaystyle (0,0,1/c)}$.

Aus der Normalenform ${\displaystyle {\vec {x}}\cdot {\vec {n}}={\vec {p}}\cdot {\vec {n}}}$ einer Ebene mit Stützvektor ${\displaystyle {\vec {p}}=(p_{1},p_{2},p_{3})^{T}}$ und Normalenvektor ${\displaystyle {\vec {n}}=(n_{1},n_{2},n_{3})^{T}}$ erhält man durch Ausmultiplizieren die Gleichung

${\displaystyle n_{1}x+n_{2}y+n_{3}z=p_{1}n_{1}+p_{2}n_{2}+p_{3}n_{3}}$.

Hierbei handelt es sich schon um die allgemeine Koordinatenform der Ebene mit ${\displaystyle a=n_{1},~b=n_{2},~c=n_{3},~d=p_{1}n_{1}+p_{2}n_{2}+p_{3}n_{3}}$.

Liegt eine Ebene in hessescher Normalform vor, kann der Parameter ${\displaystyle d}$ auch von dort übernommen werden.

Aus der Parameterform ${\displaystyle {\vec {x}}={\vec {p}}+s{\vec {u}}+t{\vec {v}}}$ einer Ebene wird zunächst deren Normalenform ${\displaystyle {\vec {x}}\cdot {\vec {n}}={\vec {p}}\cdot {\vec {n}}}$ bestimmt. Dafür wird ein Normalenvektor benötigt, den man am einfachsten als Kreuzprodukt ${\displaystyle {\vec {n}}={\vec {u}}\times {\vec {v}}}$ erhält. Aus der Normalenform gelangt man dann durch Ausmultiplizieren zur Koordinatenform.

Analog lässt sich auf diese Weise auch aus der Dreipunkteform einer Ebenengleichung ein Normalenvektor ermitteln und daraus dann die allgemeine Koordinatenform.

Alternativ kann man die Koordinatenform herleiten, indem man zunächst einen der beiden Parameter aus je zwei Gleichungen des linearen Gleichungssystems

${\displaystyle {\begin{matrix}x=p_{1}+su_{1}+tv_{1}\ &({\text{I}})\\y=p_{2}+su_{2}+tv_{2}\ &({\text{II}})\\z=p_{3}+su_{3}+tv_{3}\ &({\text{III}})\end{matrix}}}$

eliminiert und dann aus den dadurch erhaltenen Gleichungen auch den zweiten.

Allgemein wird durch eine lineare Gleichung mit ${\displaystyle n}$ Unbekannten ${\displaystyle x_{1},\dotsc ,x_{n}}$ eine Hyperebene im ${\displaystyle n}$-dimensionalen euklidischen Raum beschrieben. Eine Hyperebene besteht dann aus denjenigen Punkten ${\displaystyle (x_{1},\dotsc ,x_{n})}$, deren Koordinaten die Gleichung

${\displaystyle a_{1}x_{1}+\dotsb +a_{n}x_{n}=b}$

erfüllen. Hierbei muss zumindest einer der Parameter ${\displaystyle a_{1},\dotsc ,a_{n}}$ ungleich null sein.^[4]

• Steffen Goebbels, Stefan Ritter: Mathematik verstehen und anwenden. Springer, 2011, ISBN 978-3-8274-2762-5. 
• Peter Knabner, Wolf Barth: Lineare Algebra: Grundlagen und Anwendungen. Springer, 2012, ISBN 978-3-642-32186-3. 

• Ebene von Normalform in Koordinatenform umwandeln. In: Serlo. Abgerufen am 23. Februar 2014. 
• Ebene von Parameterform in Koordinatenform umwandeln. In: Serlo. Abgerufen am 23. Februar 2014. 

1. ↑ Die Begriffe allgemeinen Form und Koordinatenform werden in der Literatur uneinheitlich gebraucht und ihre Verwendung hängt im Wesentlichen vom Kontext ab: Werden zum Beispiel im Rahmen einer Untersuchung lediglich verschiedene Typen von Koordinatengleichungen betrachtet, so ist die Bezeichnung allgemeine Form üblich. Wird hingegen die allgemeine Koordinatengleichung als einziger Typ von Koordinatengleichungen betrachtet und zum Beispiel einer Parametergleichung gegenübergestellt (wie etwa bei der Behandlung von Ebenen im Rahmen der Schulmathematik), so wird manchmal nur von der Koordinatenform gesprochen.
2. ↑ Da der Richtungsvektor per Voraussetzung nicht der Nullvektor sein kann, wird stets mindestens eine seiner Komponenten ungleich null sein.

1. ↑ Gerd Fischer: Lernbuch Lineare Algebra und Analytische Geometrie. 4. Auflage. Springer Spektrum, Wiesbaden 2019, ISBN 978-3-658-27342-2, S. 17. 
2. ↑ Michael Jung: Ebene Trigonometrie & Analytische Geometrie. 1. Auflage. Springer Spektrum, Wiesbaden 2024, ISBN 978-3-658-03261-6, S. 183. 
3. ↑ Alexei Wassiljewitsch Pogorelow: Analytical Geometry. Mir Publishers, Moskau 1980, S. 32 (archive.org). 
4. ↑ Peter Knabner, Wolf Barth: Lineare Algebra: Grundlagen und Anwendungen. Springer, 2012, S. 41–42.