Additionsverfahren (Mathematik)

Das Additionsverfahren ist ein Verfahren zur Lösung von Gleichungssystemen. In der Schulmathematik wird es neben dem Einsetzungsverfahren und dem Gleichsetzungsverfahren standardmäßig zur Lösung von linearen Gleichungssystemen mit zwei Variablen eingesetzt.^[1] Darüber hinaus basiert das bekannteste Verfahren zur Lösung von allgemeinen linearen Gleichungssystemen, das Gaußsche Eliminationsverfahren, auf dem Additionsverfahren.

Beim Additionsverfahren werden Gleichungen addiert. Dies geschieht in der Regel so, dass eine oder mehrere Unbekannte in den Gleichungen verschwinden („eliminiert“ werden). Dazu werden die Gleichungen ggf. vorher mit geeigneten Zahlen multipliziert.^[2]

Als Beispiel soll das folgende lineare Gleichungssystem gelöst werden:

${\displaystyle {\begin{matrix}({\text{I}})\quad &5x&+&3y&=&5\\({\text{II}})\quad &2x&-&3y&=&2\end{matrix}}}$

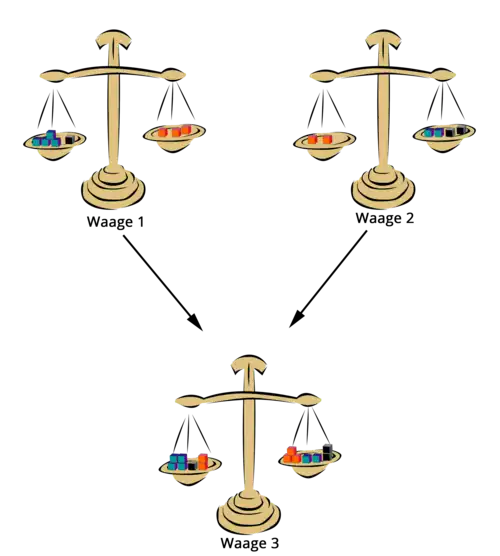
Man kann sich beide Gleichungen als ausgeglichene Waagen vorstellen. Waage 1 hat in der linken Schale ${\displaystyle 5x+3y}$ und in der rechten ${\displaystyle 5}$ liegen. Waage 2 hat in der linken Schale ${\displaystyle 2x-3y}$ und in der rechten ${\displaystyle 2}$ liegen.

Legt man die Inhalte der linken Schalen zusammen, müssen diese so viel wiegen wie die rechten Schalen zusammen. Als Gleichung erhält man:

${\displaystyle {\begin{matrix}({\text{I}})+({\text{II}}):\quad &(5x+3y)&+&(2x-3y)&=&5+2\end{matrix}}}$

Sortiert man die linke Seite der Gleichung nach den Unbekannten, heben sich die Terme mit ${\displaystyle y}$ weg und man erhält eine Lösung für ${\displaystyle x}$:

${\displaystyle {\begin{matrix}5x+2x&+&3y-3y&=&7\\7x&+&0&=&7&|:7\\x&&&=&1\end{matrix}}}$

Auch das vorherige Vervielfachen einer Gleichung ändert nichts am Gleichgewicht der jeweiligen Waage. Ein Mehrfachadditionsverfahren wie ${\displaystyle ({\text{I}})+3\cdot ({\text{II}})}$ oder ein Subtraktionsverfahren wie ${\displaystyle ({\text{I}})-({\text{II}})}$ ist also lediglich eine abkürzende Schreibweise für eine Äquivalenzumformung mit anschließendem Additionsverfahren. Für ${\displaystyle ({\text{I}})+3\cdot ({\text{II}})}$ wird die zweite Gleichung zunächst verdreifacht und dann beide Gleichungen addiert (ein ausführliches Beispiel dazu steht unten). Für ${\displaystyle ({\text{I}})-({\text{II}})}$ wird die zweite Gleichung zunächst auf beiden Seiten mit ${\displaystyle (-1)}$ multipliziert und dann beide Gleichungen addiert.

Mit Hilfe des Additionsverfahrens soll das folgende Gleichungssystem gelöst werden:

${\displaystyle {\begin{matrix}({\text{I}})&5x&+&3y&=&5\\({\text{II}})&3x&+&y&=&-1\end{matrix}}}$

Dazu muss eine der beiden Gleichungen so umgeformt werden, dass bei einer Addition der beiden Gleichungen eine Variable verschwindet. In diesem Beispiel wird dazu Gleichung ${\displaystyle ({\text{II}})}$ mit ${\displaystyle -3}$ multipliziert und man erhält das gleichwertige Gleichungssystem

${\displaystyle {\begin{matrix}({\text{I}})&5x&+&3y&=&5\\({\text{II'}})&-9x&-&3y&=&3\end{matrix}}}$

Diese beiden Gleichungen werden nun addiert und somit in einer Gleichung zusammengefasst:

${\displaystyle {\begin{matrix}(5x-9x)&+&(3y-3y)&=&5+3\\-4x&+&0y&=&8\\-4x&&&=&8\end{matrix}}}$

Anschließend löst man nach der verbliebenen Variablen ${\displaystyle x}$ auf und erhält ${\displaystyle x=-2}$. Dieser Wert wird nun in Gleichung ${\displaystyle ({\text{I}})}$ eingesetzt:

${\displaystyle 5\cdot (-2)+3y=5}$

Durch Auflösen erhält man den Wert der zweiten Variablen als ${\displaystyle y=5}$. Die Lösungsmenge ist somit ${\displaystyle \mathbb {L} =\{(-2|5)\}}$.

Es wird das folgende nichtlineare Gleichungssystem betrachtet:

${\displaystyle {\begin{aligned}&({\text{I}})&x^{2}+2y&=9\\&({\text{II}})&-2x^{2}+2y&=6\end{aligned}}}$

Um die quadratischen Terme zu eliminieren, wird Gleichung ${\displaystyle ({\text{II}})}$ durch 2 geteilt und man erhält das gleichwertige Gleichungssystem

${\displaystyle {\begin{aligned}&({\text{I}})&x^{2}+2y&=9\\&({\text{II'}})&-x^{2}+y&=3\end{aligned}}}$

Durch die Addition ${\displaystyle ({\text{I}})+({\text{II'}})}$ erhält man die Gleichung ${\displaystyle 3y=12}$, woraus sofort ${\displaystyle y=4}$ folgt. Einsetzen z. B in Gleichung ${\displaystyle ({\text{I}})}$ liefert

${\displaystyle x^{2}+8=9}$.

Durch Auflösen erhält man die Werte der zweiten Variable als ${\displaystyle x_{1}=1}$ und ${\displaystyle x_{2}=-1}$. Die Lösungsmenge ist somit

${\displaystyle \mathbb {L} =\{(-1;4),(1;4)\}}$.

• Einsetzungsverfahren
• Gleichsetzungsverfahren

1. ↑ Hans-Georg Weigand, Alexander Schüler-Meyer, Guido Pinkernell: Didaktik der Algebra. 4. Auflage. Springer, 2022, ISBN 978-3-662-64659-5, S. 295. 
2. ↑ Andreas Filler: Elementare Lineare Algebra (= Mathematik Primarstufe und Sekundarstufe I + II). Spektrum Akademischer Verlag, Heidelberg 2011, ISBN 978-3-8274-2412-9, S. 9.